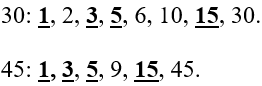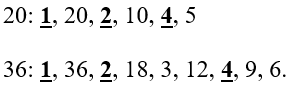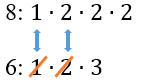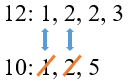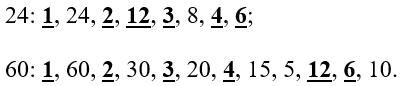Как найти наибольший делитель чисел 5 класс

Математика

5 класс

Урок № 43

Наибольший общий делитель (НОД)

Перечень рассматриваемых вопросов:

– делители числа;

– кратные числа;

– разложение на простые множители;

– НОД.

Тезаурус

Простое число – это натуральное число, которое больше 1 и делится только на 1 и само на себя.

Составные числа – это непростые натуральные числа больше 1.

Взаимно простые числа – это числа, которые не имеют общих простых делителей.

Обязательная литература:

1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература:

1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. ­– 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Начнём наше занятие словами известной поговорки: «Учить – ум точить». Сегодня мы будем оттачивать умение находить общие делители сразу нескольких чисел.

Итак, рассмотрим два числа: 12 и 15. Выпишем все делители этих чисел. 12 – делители 1, 2, 3, 4, 6, 12.

15 – делители 1, 3, 5, 15.

Найдём общие делители этих чисел – это числа 1 и 3. Введём новое понятие – «наибольший общий делитель», который кратко обозначают НОД.

У этих чисел наибольший общий делитель равен 3.

Записывается – НОД (12; 15) = 3. НОД чисел двенадцать и пятнадцать равен трём.

Правило нахождения НОД:

1. разложим числа на простые множители;
2. подчеркнём одинаковые множители этих чисел;
3. перемножим общие множители одного из чисел, это и будет НОД заданных чисел.

Найдём НОД чисел 15 и 16.

НОД (15; 16) = ?

Разложим числа на простые множители.

Видно, что из всех множителей – общий лишь 1.

Такие числа, которые не имеют общих простых делителей, называются взаимно простыми числами. Любые два простых числа или два соседних натуральных числа будут взаимно простыми.

Найдём НОД (10; 100).

Разложим числа на простые множители.

Выделим общие делители у этих чисел, это 2 и 5.

Умножим их и получим наибольший общий делитель: НОД (10; 100) = 2 · 5 = 10.

Обратите внимание на то, что 100 делится нацело на 10 и НОД тоже равен 10. Поэтому можно сделать вывод: если одно из двух чисел делится нацело на другое, то НОД этих чисел равен меньшему из них.

Найдём наибольший общий делитель трёх чисел.

НОД (42; 70; 98) = ?

Разложим числа на простые множители:

Выделим общие делители у этих чисел, это 2 и 7.

Умножим их и получим наибольший общий делитель: НОД (42; 70; 98) = 2 · 7 = 14

Некоторые задачи можно решить при помощи НОД проще, чем каким-либо другим способом.

Например, решим такую задачу.

Для участия в соревнованиях нужно разделить 35 детей в возрасте 14 лет и 21 ребёнка в возрасте 12 лет на команды так, чтобы они состояли только из одновозрастных спортсменов. Какое наибольшее число участников одного возраста может быть в команде?

Решение: чтобы решить эту задачу нужно найти НОД (21; 35).

Разложим числа на простые множители:

Следовательно, НОД (21; 35) = 7 – это и будет наибольшим числом участников в команде.

Ответ: 7 человек.

Тренировочные задания

№ 1. Какую цифру нужно подставить в число НОД (7; 2_) вместо пропуска, чтобы получить НОД = 7?

Варианты ответов: 1, 2, 3.

Решение: разложим на множители оба числа, при этом вместо пропуска подставим по порядку все цифры. А далее найдём подходящий НОД этих чисел, равный 7. Получим следующее разложение:

Из всех разложений на множители под НОД (7; 2) = 7 подходит только число 21.

Ответ: искомая цифра – 1.

№ 2. В продуктовых наборах должно быть одинаковое количество груш и апельсинов. Всего приготовили 120 груш и 126 апельсинов. В какое наибольшее количество наборов можно разложить их поровну?

Решение: чтобы решить эту задачу, нужно найти НОД заданных чисел, он и будет являться искомым ответом, т. е. наибольшим количеством наборов при равном разложении фруктов.

НОД (120; 126) = 2 · 3 = 6

Ответ: 6 наборов.

Наибольшим общим делителем (НОД) двух целых чисел называется наибольший из их общих делителей. К примеру для чисел 12 и 8, наибольшим общим делителем будет 4.

Как найти НОД?

Способов найти НОД несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОД при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:

1. разложить оба числа на простые множители (подробнее о разложении чисел на простые множители смотрите тут);
2. выбрать одинаковые множители, входящие в оба разложения;
3. найти их произведение.

Примеры нахождения наибольшего общего делителя

Рассмотрим приведенный алгоритм на конкретных примерах:

Пример 1: найти НОД 12 и 8

2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 2 и 2

3. Перемножаем эти множители и получаем: 2 · 2 = 4

Ответ: НОД (8; 12) = 2 · 2 = 4.

Пример 2: найти НОД 75 и 150

Этот пример, как и предыдущий с легкостью можно высчитать в уме и вывести ответ 75, но для лучшего понимания работы алгоритма, проделаем все шаги:

2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 3, 5 и 5

3. Перемножаем эти множители и получаем: 3 · 5 · 5 = 75

Ответ: НОД (75; 150) = 3 · 5 · 5 = 75.

Частный случай или взаимно простые числа

Нередко встречаются ситуации, когда оба числа взаимно простые, т.е. общий делитель равен единице. В этом случае, алгоритм будет выглядеть следующим образом:

Пример 3: найти НОД 9 и 5

Видим, что одинаковых множителей нет, а значит, что это частный случай (взаимно простые числа). Общий делитель — единица.

НОК и НОД

Рассмотрим выражение:

(45:9)

Можем сказать, что 45 – делимое, а 9 – делитель данного выражения.

Мы знаем, что 45 делится нацело на число 9. В таком случае, если мы захотим описать, чем эти числа являются друг другу, то мы скажем, что

9 – делитель числа 45

45 – кратно числу 9

Иногда при решении задач нужно находить общие кратные или общие делители двух чисел.

Наименьший делитель двух чисел – всегда единица. Такой делитель нет смысла искать, поэтому ищут наибольший общий делитель.

А кратных наоборот – бесконечно много, невозможно искать наибольшее из них, поэтому ищут, наименьшее общее кратное.

НОД:

Наибольший общий делитель (НОД) двух чисел – это наибольшее число, на которое каждое из этих чисел можно поделить без остатка.

Пример №1:

Рассмотрим числа 30 и 45.

1. Найдем все их существующие делители, т.е. числа, на которые каждое из них поделится нацело:

1. Мы видим, что у этих двух чисел есть несколько общих делителей. Наибольший из них – 15 – является самым большим. Это и есть НОД.

Значит и число 45 и число 30 можно нацело поделить на 15. Записывают это так:

(НОД (30;45) = 15)

Ответ: 15.

Пример №2:

Найдем (НОД (20;36):)

1. Выпишем все делители этих чисел.

Так же делители можно сразу записывать парой. Если 20 нацело делится на 2, то

(20 : 2 = 10)

Значит 10 – тоже делитель числа 20. Запишем делители 2 и 10 парой:

1. Выделим все общие делители и найдем наибольший из них. В данном случае

(НОД(20;35) = 4.)

Ответ: 4.

НОК:

Наименьшее общее кратное (НОК) двух чисел – это наименьшее число, которое можно поделить на каждое из этих чисел без остатка.

Пример №3:

Найдем (НОК (10;12).)

1. Возьмем наименьшее число. В данном случае – 10.

Будем умножать его на натуральные числа по порядку, пока не получим число, кратное 12, то есть такое, на которое нацело поделится и 10, и 12. Оно и будет НОК этих двух чисел. Такой метод называется методом подбора.

(10 bullet 1 = 10; 10 НЕ кратно 12)

(10 bullet 2 = 20; 20 НЕ кратно 12)

(10 bullet 3 = 30; 30 НЕ кратно 12)

(10 bullet 4 = 40; 40 НЕ кратно 12)

(10 bullet 5 = 50; 50 НЕ кратно 12)

(10 bullet 6 = 60; 60 кратно 12)

1. Первое число, которое будет кратно обоим числам и является их наименьшим общим кратным.

Общих кратный, в отличии от делителей, бесконечно много, поэтому обычно выбирают наименьший их них.

Ответ: 60.

Также можно находить НОК через разложение на множители:

Пример №4:

Найдём (НОК (6;8):)

1. Разложим числа 6 и 8 на простейшие множители, т.е. представим каждое число как произведения простых чисел. Множители большего числа запишем сверху:

8: (1 bullet 2 bullet 2 bullet 2)

6: (1 bullet 2 bullet 3)

1. Видим, что множители 1 и 2 повторяются у обоих чисел, поэтому для меньшего числа их уберем. Останется:

1. Перемножим все оставшиеся числа. Их произведение и будет НОК:

(НОК (6; 8) = 1 bullet 2 bullet 2 bullet 2 bullet 3 = 24)

Ответ: 24.

Пример №5:

Найдем (НОК (10;12)) разложением на множители:

1. Разложим оба числа на простые множители. Сверху запишем большее число:

12: 1, 2, 2, 3

10: 1, 2, 5

1. Для меньшего числа зачеркнем те множители, которые уже есть у большего числа:

1. Перемножим все оставшиеся числа:

(НОК (10; 12) = 1 bullet 2 bullet 2 bullet 3 bullet 5 = 60)

Наш ответ совпал с ответом, где мы использовали метод подбора.

Ответ: 60.

ВЗАИМОСВЯЗЬ НОК И НОД:

Произведение НОК и НОД некоторых чисел равно произведению самих этих чисел:

(НОК(a; b) bullet НОД(a; b) = a bullet b)

Докажем эту формулу на примере.

Пример №6:

Рассмотрим пару чисел 24 и 60.

1. Найдем их НОД:

(НОД (24;60) = 12)

1. Найдем их НОК:

(НОК (24; 60) = 1 bullet 2 bullet 2 bullet 2 bullet 3 bullet 5 = 120)

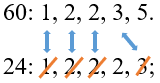
1. Рассмотрим поближе НОК. Чтобы его получить, мы переменожили все простые множители чисел 60 и 24 за исключением множителей 1, 2, 2, 3. Найдем отдельно их произведение:

(1 bullet 2 bullet 2 bullet 3 = 12)

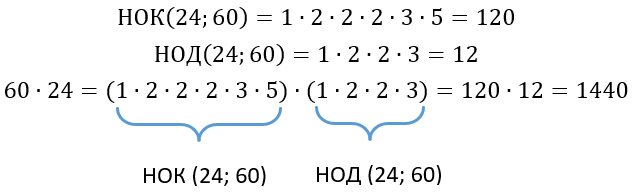
Если перемножить все простые множители числе 60 и 24 мы получим просто их произведение, при этом оно будет состоять из НОК и числа 12, которое в свою очередь равно НОД:

ГОСУДАРСТВЕННОЕ
БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЯЯ
ОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 377

КИРОВСКОГО
РАЙОНА САНКТ-ПЕТЕРБУРГА

Тема: «НОД и
НОК.»

Памятка
по математике

Для
учеников 5 класса

Автор:
Кудрявцева Лилия Викторовна

НОД и НОК

9

1, 3, 9                                           18, 27, 36, 45 …

НОД	НОК
Наибольший общий делитель (НОД) двух данных чисел a и b – это наибольшее число, на которое оба числа a и b делятся без остатка.	Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое делится нацело на каждое из этих чисел.
I способ нахождения НОД методом перебора делителей 1. Найти делители каждого числа; 2. Найти общие делители; 3. Выбрать наибольший общий делитель. Найти НОД 10 и 15. Д (10) = {1, 2, 5, 10} Д (15) = {1, 3, 5, 15} Д (10, 15) = {1, 5} НОД (10; 15) = 5	I способ нахождения НОК методом перебора кратных 1. Берем большее из чисел 2. Находим числа кратные выбранному (умножая выбранное число последовательно на 1, 2, 3, 4, 5 , и тд) 3. Каждое полученное кратное проверяем делится ли оно на оставшиеся число; первое такое кратное и есть НОК. Найти НОК 18 и 24 24•1=24  (не делится на 18) 24•2=48   (не делится на 18) 24•3=72  –  делится на 18 НОК (24, 18)=72
II способ нахождения НОД через разложения на простые множители 1. Разложить числа на простые множители; 2. Подчеркнуть одинаковые простые множители в  обоих числах; 3. Найти произведение одинаковых простых множителей и записать ответ. Найти НОД  48 и 36. НОД (48; 36) = 2 • 2 • 3 = 12	II способ нахождения НОК через разложения на простые множители 1. Разложить на простые множители каждое число; 2. Выписать все множители из разложения одного любого числа; 3. Добавить к ним недостающие множители из разложения другого числа; 4. Найти произведение получившихся множителей. Найти НОК  24 и 60. 60 = 2 • 2 • 3 • 5   24 = 2 • 2 • 2 • 3                                                                 60 НОК (24; 60) = 2 • 2 • 3 • 5 • 2 =120
Примечание 1: Если a и b взаимно простые* числа, то НОД(a,b)=1 Например:     НОД(4,9)=1	Примечание 1: Если a и b взаимно простые* числа, то НОК(a,b)=a•b Например:     НОК(4, 9)=4•9=36
Примечание 2:  Если a делится на b, то НОД(a,b)=b Например: НОД(120, 60)=60	Примечание 2:  Если a делится на b, то НОК(a,b)=a Например: НОК(120, 60)=120

*Взаимно
простые числа – это те, у которых нет общих
простых делителей. (Например: 4 и 9)

Примечание 1:  Простые числа (1,2,3,5,7,11,13,17 и т.д.) –
взаимно просты

Примечание 2:  Два соседних
натуральных числа (например:  24 и 25) –  взаимно просты

11. Что называется наибольшим общим делителем НОД двух чисел?

Наибольшим общим делителем НОД двух чисел m и n называется такое наибольшее число D, на которое m и n делятся без остатка.Можно подбором найти НОД двух чисел или раскладывая на множители.Разложив на множители первое и второе число и взяв общие сомножители (те которые входят и в первое и второе разложение), и перемножив получим наибольший общий делитель НОД.

12. Что называется наименьшим общим кратным?

Наименьшим общим кратным НОК двух чисел m и n называется такое наименьшее число К, которое само делится на m и n без остатка.Можно подбором найти НОК двух чисел или раскладывая на множители.Разложив на множители первое и второе число и взяв разложение одного числа (лучше большего) и дописав из второго разложения недостающие сомножители и перемножив получим наибольшее общее кратное НОК.

13. Какие два числа называются взаимно простыми?

Два числа называются взаимно простыми, если у них наибольший общий делитель равен единице. Например, 8 и 9 – числа составные, но наибольшее число на которое 8 и 9 делятся без остатка равно 1.