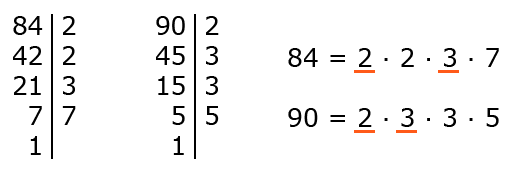Как найти наибольший меньший делитель

Делимость

До того как начать разбирать эти две аббревиатуры, рассмотрим сначала понятие делимости. Что значит фраза “число А делится на число Б”? Например, 24 делится на 6. И что значит “не делится”? Например, 27 не делится на 2.

Когда мы говорим о делимости, то речь идет о целочисленном делении целых чисел. И делимость означает, что число делится на делитель нацело, без остатка.

24 делится на 6, частное равно 4, а остаток нулю.

27 не делится на 2, частное равно 13, а остаток равен одному.

Признаки делимости

Проверить, делится ли одно число на заданное, можно просто выполнив деление. Но если число большое, а результат самого деления нам не так чтобы нужен? Можно ли не находя частное, определить, делится ли число?

Существуют несколько признаков делимости, когда по внешнему вида числа мы можем определить, делится ли оно на заданное. Рассмотрим только некоторые из них, те, которые легко проверяются.

По последней цифре

Число делится на 2, если его последняя цифра – четная.

Число делится на 5, если его последняя цифра – 5 или 0.

Число делится на 10, если его последняя цифра – 0.

Например, 234 делится на 2, так как 4 – четная.

235 делится на 5, так как последняя цифра – 5.

190 делится на 10 и на 5, так как последняя цифра – 0.

По сумме цифр числа

Число делится на 3, если сумма цифр этого числа делится на 3.

Число делится на 9, если сумма цифр этого числа делится на 9.

Например, 393 делится на 3, так как сумма цифр этого числа 3+9+3=15 делится на 3.

180 делится на 9, так как сумма цифр этого числа 1+8+0=9 делится на 9.

Число делится на 6, если оно делится на 2 и на 3 одновременно.

Например, 36 делится на 2 (6 четная) и на 3 (3+6=9 – делится на 3), поэтому оно делится на 6.

Простые и составные числа

Среди натуральных чисел выделяют такие числа, которые делятся только на 1 и на самого себя. Такие числа называются простыми. Остальные числа, имеющие больше двух делителей, называют составными. Отдельно выделяют 1, у нее только один делитель.

Пример простого числа – 2, 3, 5, 7, 11, 13, 17, 19 и так далее. Существуют специальные таблицы простых чисел, но многие проблемы простых чисел до сих пор не решены.

Разложение на простые множители

Для составных чисел можно найти такие множители, которые будут только простыми числами, а произведение этих множителей будет равно исходному числу.

Например, 24=2*2*2*3.

Это произведение и называется разложением на простые множители. Если множители отсортированы по возрастанию, то для каждого конкретного числа это разложение будет единственным.

Для построения такого разложения существует четкий алгоритм.

1. Записываем в левый столбец исходное число, проводим вертикальную черту, отделяя правый столбец.
2. Проверяем, делится ли число на 2. Если да, то записываем 2 в правый столбец, в левый столбец в следующей строке записываем кратное исходного числа и 2.
3. Проверяем, делится ли полученное число на 2, если да, то действуем как в пункте 2.
4. Если нет, то проверяем, делится ли наше число на 3. Если да, то 3 записываем в правый столбец, а в левый столбец строчкой ниже пишем кратное от деления на 3 и переходим к пункту 3.
5. Если число не делится на 3, то переходим к следующему числу в списке простых чисел – 5.
6. Каждый раз начинаем проверку делимости с 2, постепенно переходя к все большим и большим простым числам, если это необходимо.
7. Так действуем до тех пор, пока число в левом столбце не станет равно 1. Тогда останавливаемся.
8. В правом столбце у нас записаны все простые множители числа.

Наибольший общий делитель

НОД или наибольший общий делитель для нескольких чисел – это такое наибольшее число, на которое делятся все эти числа.

Например, НОД(12, 18)=6.

Зная разложение чисел на простые множители, легко найти их НОД. Выписываем совпадающие множители, их произведение и даст нам НОД.

Наименьшее общее кратное

НОК или наименьшее общее кратное нескольких чисел – это такое наименьшее число, которое делится на все эти числа.

Например, НОК(4, 6)=12.

Зная разложение чисел на простые множители, легко найти их НОК. К множителям меньшего числа дописываем несовпадающие множители. Это произведение и даст нам НОК.

Взаимно простые числа

Если у двух составных чисел нет общих простых множителей, то такие числа называются взаимно простыми. НОК таких чисел равен их произведению, а НОД равен 1.

Нахождение НОК и НОД двух натуральных чисел

Содержание:

• Что такое НОК и НОД двух натуральных чисел
• Особенности вычисления, алгоритм Евклида
• Правило нахождения наибольшего общего делителя (НОД)
• Правило нахождения наименьшего общего кратного (НОК)

Что такое НОК и НОД двух натуральных чисел

Натуральными числами называют числа, которые используются при счете – 1, 2, 3, 16, 25, 101, 2560 и далее до бесконечности. Ноль, отрицательные и дробные или нецелые числа не относятся к натуральным.

Наименьшее общее кратное (НОК) двух натуральных чисел a и b – это наименьшее число, которое делится без остатка на каждое из рассматриваемых чисел.

Наибольший общий делитель (НОД) двух натуральных чисел a и b – это наибольшее число, на которое делится без остатка каждое рассматриваемое число.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Свойства НОК и НОД для натуральных чисел a и b

• (НОД (a, b) = НОД (b, a);)
• (НОК (a, b) = НОК (b, a);)
• (НОК;(a,b)=frac{a;times;b}{НОД;(a,b)}.)

Особенности вычисления, алгоритм Евклида

Рассмотрим два способа определения НОД и НОК с помощью алгоритма Евклида:

• Способ деления.

При делении целых чисел с остатком, где a – делимое, b – делитель (b не равно 0) находят целые числа q и r согласно равенству (a=btimes) q+r, в котором q – неполное частное, r – остаток при делении (не отрицательное, по модулю меньше делителя).

Чтобы вычислить НОД, первоначально нужно выбрать наибольшее из двух чисел и поделить его на меньшее. Пока остаток не станет равным нулю, повторяется цикл деления делителя на остаток от деления в соответствии с формулой.

Пример №1

Вычислим НОД для чисел 12 и 20. Делим 20 на 12 и получаем 1 и 8 в остатке. Запишем иначе:

(20=12times1+8), так как остаток не равняется нулю, продолжаем деление. Делим 12 на 8 и получаем 1 и 4 в остатке. Записываем: (12=8times1+4) и по аналогии делим 8 на 4 и получаем 2 и 0 в остатке. НОД равен остатку, предшествующему нулю.

НОД (12;20) = 4

НОК получаем согласно свойству (НОК (a, b) = НОК;(a,b)=frac{a;times;b}{НОД;(a,b)}.) Подставляем числовые значения:

НОК (12; 20) = (12times20div4=60)

НОК (12;20) = 60

• Способ вычитания.

Здесь повторяется цикл вычитания из наибольшего числа меньшего числа до момента, пока разность не станет равна нулю. НОД равен предшествующей нулю разности.

Пример №2

Вычислим НОД для тех же чисел, 12 и 20.

20 – 12 = 8 (разность не равна нулю, продолжаем)

12 – 8 = 4

8 – 4 = 4

4 – 4 = 0

НОД (12;20) = 4

НОК находим также, как и при методе деления.

Правило нахождения наибольшего общего делителя (НОД)

Для нахождения наибольшего общего делителя воспользуемся пошаговым алгоритмом:

1. Разложить числа на простые множители.
2. Найти общий множитель одного и другого числа.
3. Перемножить общие множители, если их несколько, и их произведение будет НОД.

Пример №3

Возьмем натуральные числа 24 и 36.

(24=2times2times2times3)

(36=2times2times3times3)

Правильно записать следующим образом:

(НОД (24;36)=2times3=6)

Примечание

В случае, когда одно или оба числа относятся к простым, т.е. делятся только на единицу и на само себя, то их НОД равняется 1.

Правило нахождения наименьшего общего кратного (НОК)

Для нахождения наименьшего общего кратного воспользуемся подробным алгоритмом:

1. Наибольшее из чисел, а затем остальные разложить на простые множители.
2. Выделить те множители, которые отсутствуют у наибольшего.
3. Перемножить множители п. 2 и множители наибольшего числа, получить НОК.

Пример №4

Возьмем натуральные числа 9 и 12.

(12=2times2times3)

(9=3times3) (видим, что у числа 12 отсутствует одна тройка)

Правильно записать следующим образом:

(НОК (9;12)=2times2times3times3=36)

Текст с ошибкой:

Расскажите, что не так

Одной из задач, вызывающих проблему у современных школьников, привыкших к месту и не к месту использовать калькуляторы, встроенные в гаджеты, является нахождение наибольшего общего делителя (НОД) двух и более чисел.

Невозможно решить никакую математическую задачу, если неизвестно, о чём собственно спрашивают. Для этого нужно знать, что означает то или иное выражение, используемое в математике.

Общие понятия и определения

Необходимо знать:

1. Если некое число можно использовать для подсчёта различных предметов, например, девять столбов, шестнадцать домов, то оно является натуральным. Самым маленьким из них будет единица.
2. Когда натуральное число делится на другое натуральное число, то говорят, что меньшее число — это делитель большего.
3. Если два и более различных числа делятся на некое число без остатка, то говорят, что последнее будет их общим делителем (ОД).
4. Самый большой из ОД именуется наибольшим общим делителем (НОД).
5. В таком случае, когда у числа есть только два натуральных делителя (оно само и единичка), оно называется простым. Самое маленькое среди них – двойка, к тому же она и единственное чётное в их ряду.
6. В случае если у двух чисел максимальным общим делителем является единица, то они будут взаимно простыми.
7. Число, у которого больше чем два делителя, именуется составным.
8. Процесс когда находятся все простые множители, которые при умножении между собой дадут в произведении начальное значение в математике называют разложением на простые множители. Причём одинаковые множители в разложении могут встречаться неоднократно.

В математике приняты следующие записи:

1. Делители Д (45) = (1;3;5;9;45).
2. ОД (8;18) = (1;2).
3. НОД (8;18) = 2.

Различные способы найти НОД

Проще всего ответить на вопрос как найти НОД в том случае, когда меньшее число является делителем большего. Оно и будет в подобном случае наибольшим общим делителем.

Например, НОД (15;45) = 15, НОД (48;24) = 24.

Но такие случаи в математике являются весьма редкими, поэтому для того, чтобы находить НОД используются более сложные приёмы, хотя проверять этот вариант перед началом работы все же весьма рекомендуется.

Способ разложения на простые сомножители

Если необходимо найти НОД двух или более различных чисел, достаточно разложить каждое из них на простые сомножители, а затем произвести процесс умножения тех из них, которые имеются в каждом из чисел.

Пример 1

Рассмотрим, как находить НОД 36 и 90:

1. 36 = 1*2*2*3*3;
2. 90 = 1*2*3*3*5;

НОД (36;90) = 1*2*3*3 = 18.

Теперь посмотрим как находить то же самое в случае трёх чисел, возьмём для примера 54; 162; 42.

Как разложить 36 мы уже знаем, разберёмся с остальными:

1. 162 = 1*2*3*3*3*3;
2. 42 = 1*2*3*7;

Таким образом, НОД (36;162;42) = 1*2*3 = 6.

Следует заметить, что единицу в разложении писать совершенно необязательно.

Рассмотрим способ, как просто раскладывать на простые множители, для этого слева запишем необходимую нам цифру, а справа станем писать простые делители.

Разделять колонки можно, как знаком деления, так и простой вертикальной чертой.

1. 36 / 2 продолжим наш процесс деления;
2. 18 / 2 далее;
3. 9 / 3 и ещё раз;
4. 3 / 3 сейчас совсем элементарно;
5. 1 – результат готов.

Искомое 36 = 2*2*3*3.

Евклидов способ

Этот вариант известен человечеству ещё со времён древнегреческой цивилизации, он во многом проще, и приписывается великому математику Евклиду, хотя весьма похожие алгоритмы применялись и ранее. Этот способ заключается в использовании следующего алгоритма, мы делим большее число с остатком на меньшее. Затем наш делитель делим на остаток и продолжаем так действовать по кругу пока не произойдёт деление нацело. Последнее значение и окажется искомым наибольшим общим делителем.

Приведём пример использования данного алгоритма:

попробуем выяснить какой НОД у 816 и 252:

1. 816 / 252 = 3 и остаток 60. Сейчас 252 разделим на 60;
2. 252 / 60 = 4 в остатке на этот раз окажется 12. Продолжим наш круговой процесс, разделим шестьдесят на двенадцать;
3. 60 / 12 = 5. Поскольку на сей раз никакого остатка мы не получили, то у нас готов результат, двенадцать будет искомым для нас значением.

Итак, по завершении нашего процесса мы получили НОД (816;252) = 12.

Действия при необходимости определения НОД если задано более двух значений

Мы уже разобрались, что делать в случае, когда имеется два различных числа, теперь научимся действовать, если их имеется 3 и более.

При всей кажущейся сложности, данная задача проблем у нас уже не вызовет. Сейчас мы выбираем два любые числа и определяем искомое для них значение. Следующим шагом отыскиваем НОД у полученного результата и третьего из заданных значений. Затем снова действуем по уже известному нам принципу для четвёртого пятого и так далее.

Заключение

Итак, при кажущейся большой сложности поставленной перед нами изначально задачи, на самом деле все просто, главное уметь выполнять безошибочно процесс делений и придерживаться любого из двух описанных выше алгоритмов.

Хотя оба способа и являются вполне приемлемыми, в общеобразовательной школе гораздо чаще применяется первый способ. Это связано с тем, что разложение на простые множители понадобится при изучении следующей учебной темы — определение наибольшего общего кратного (НОК). Но все же стоит ещё раз заметить – применение алгоритма Евклида ни в коей мере не может считаться ошибочным.

Видео

С помощью видео вы сможете узнать, как найти наибольший общий делитель.

Наибольший общий делитель (НОД), свойства и формулы

О чем эта статья:

5 класс, 6 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие наибольшего общего делителя

Начнем с самого начала и вспомним, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.

Делитель натурального числа — это такое натуральное число, которое делит данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.

Общий делитель нескольких целых чисел — это такое число, которое может быть делителем каждого числа из указанного множества. Например, у чисел 12 и 8 общим делителем будет четверка. Чтобы это проверить, напишем верные равенства: 8 = 4 * 2 и 12 = 3 * 4. Но у этой пары чисел есть и другие общие делители: 1, -1 и -4.

Любое число можно разделить на 1, -1 и на само себя. Значит у любого набора целых чисел будет как минимум три общих делителя. Если общий делитель больше 0 — противоположное ему значение со знаком минус также является общим делителем.

Если b — делитель целого числа a, которое не равно нулю, то модуль числа b не может быть больше модуля числа a. Значит любое число, не равное 0, имеет конечное число делителей.

Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).

Например, для 4 и -16 НОД будет 4. Как мы к этому пришли:

Проверить результаты вычислений можно с помощью онлайн-калькулятора НОД и НОК.

1. Зафиксируем все делители четырех: ±4, ±2, ±1.
2. А теперь все делители шестнадцати: ±16, ±8, ±4, ±3 и ±1.
3. Выбираем общие: это -4, -2, -1, 1, 2 и 4. Самое большое общее число: 4. Вот и ответ.

Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.

Найдем наибольший общий делитель нескольких целых чисел: 10, 6, 44, -18. Он будет равен трем. Ответ можно записать так: НОД (12, 6, 42, -18) = 3. А чтобы проверить правильность ответа, нужно записать все делители и выбрать из них самые большие.

Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.

Помимо НОД есть еще и НОК, что расшифровывается, как наименьшее общее кратное и означает наименьшее число, которое делится на каждое из исходных чисел без остатка.

Еще один пример. Рассчитаем НОД для 28 и 64.

Распишем простые множители для каждого числа и подчеркнем одинаковые

Д (64) = 2 * 2 * 2 * 2 * 2 * 2

Найдем произведение одинаковых простых множителей и запишем ответ

НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Свойства наибольшего общего делителя

У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.

Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.

Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.

Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.

Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.

Доказательство

Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Из этого следует, что любой делитель числа b является общим делителем чисел а и b.

Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b.

В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.

• Например, НОД (25, 25) = 25.

Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.

• Например, НОД (4, 40) = 4, так как 40 кратно 4.

Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.

Доказательство

Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c.

Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым.

Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).

Доказательство

Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители.

Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.

Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.

Способы нахождения наибольшего общего делителя

Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.

1. Разложение на множители

Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.

Пример 1. Найти НОД (84, 90).

Разложим числа 84 и 90 на простые множители:

Ответ: НОД (84, 90) = 6.

Пример 2. Найти НОД (15, 28).

Разложим 15 и 28 на простые множители:

Числа 15 и 28 являются взаимно простыми, так как их наибольший общий делитель — единица.

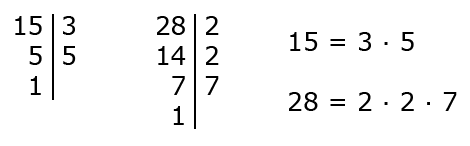
Ответ: НОД (15, 28) = 1.

Пример 3. Найти НОД для 24 и 18.

Разложим оба числа на простые множители:

НОД (24, 18) =2 * 3 = 6

Ответ: НОД (24, 18) = 6

2. Алгоритм Евклида

Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.

Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.

Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.

Пример 1. Найти НОД для 24 и 8.

Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, 8) = 8.

В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:

1. Большее число поделить на меньшее.
2. Меньшее число поделить на остаток, который получается после деления.
3. Первый остаток поделить на второй остаток.
4. Второй остаток поделить на третий и т. д.
5. Деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель и есть наибольший общий делитель.

Пример 2. Найти наибольший общий делитель чисел 140 и 96:

1. 140 : 96 = 1 (остаток 44)
2. 96 : 44 = 2 (остаток 8)
3. 44 : 8 = 5 (остаток 4)
4. 8 : 4 = 2

Последний делитель равен 4 — это значит: НОД (140, 96) = 4.

Ответ: НОД (140, 96) = 4

Пошаговое деление можно записать столбиком:

Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:

1. Найти наибольший общий делитель любых двух чисел из данных.
2. Найти НОД найденного делителя и третьего числа.
3. Найти НОД последнего найденного делителя и четвёртого числа и т. д.

Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.

Источник

Наименьшее общее кратное

Общее кратное. Наименьшее общее кратное.

Общим кратным нескольких чисел называется число, которое делится на каждое из этих чисел. Например, числа 9, 18 и 45 имеют общее кратное 180. Но 90 и 360 – тоже их общие кратные. Среди всех общих кратных всегда есть наименьшее, в данном случае это 90. Это число называется наименьшим общим кратным (НОК).

Чтобы найти наименьшее общее кратное (НОК) нескольких чисел надо:

1 ) представить каждое число как произведение его простых множителей, например:

504 = 2 · 2 · 2 · 3 · 3 · 7 ,

2) записать степени всех простых множителей:

504 = 2 · 2 · 2 · 3 · 3 · 7 = 2 3 · 3 2 · 7 1 ,

3) выписать все простые делители (множители) каждого из этих чисел;

4) выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел;

5) перемножить эти степени.

П р и м е р . Найти НОК чисел: 168, 180 и 3 0 2 4.

Р е ш е н и е . 168 = 2 · 2 · 2 · 3 · 7 = 2 3 · 3 1 · 7 1 ,

180 = 2 · 2 · 3 · 3 · 5 = 2 2 · 3 2 · 5 1 ,

3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 2 4 · 3 3 · 7 1 .

Выписываем наибольшие степени всех простых делителей

и перемножаем их :

НОК = 2 4 · 3 3 · 5 1 · 7 1 = 15120 .

Наибольший Общий Делитель

Наибольший общий делитель

Общий делитель. Наибольший общий делитель.

Общим делителем нескольких чисел называется число, которое является делите-лем каждого из них. Например, числа 36, 60, 42 имеют общие делители 2, 3 и 6. Среди всех общих делителей всегда есть наибольший, в данном случае это 6. Это и естьнаибольший общий делитель (НОД).

Чтобы найти наибольший общий делитель (НОД) нескольких чисел надо:

1) представить каждое число как произведение его простых множителей, например:

360 = 2 · 2 · 2 · 3 · 3 · 5 ,

2) записать степени всех простых множителей:

360 = 2 · 2 · 2 · 3 · 3 · 5 = 2 3 · 3 2 · 5 1 ,

3) выписать все общие делители (множители) этих чисел;

4) выбрать наименьшую степень каждого из них, встретившуюся во всех произведениях;

5) перемножить эти степени.

П р и м е р . Найти НОД чисел: 168, 180 и 3024.

Р е ш е н и е . 168 = 2 · 2 · 2 · 3 · 7 = 2 3 · 3 1 · 7 1 ,

180 = 2 · 2 · 3 · 3 · 5 = 2 2 · 3 2 · 5 1 ,

3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 2 4 · 3 3 · 7 1 .

Выпишем наименьшие степени общих делителей 2 и 3

и перемножим их:

НОД = 2 2 · 3 1 = 12 .

Множители

Простые и составные числа

Все целые числа (кроме 0 и 1) имеют минимум два делителя: 1 и самого себя. Числа, не имеющие других делителей, называютсяпростыми числами. Числа, имеющие другие делители, называются составными (или сложными) числами. Простых чисел – бесконечное множество. Ниже приведены простые числа, не превосходящие 200:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,

47, 53 , 59, 61, 67, 71, 73, 79, 83, 89, 97, 101,

103, 107, 109, 113, 127, 131, 137, 139, 149, 151,

157, 163, 167, 173, 179, 181, 191, 193, 197, 199.

Разложение на простые множители

Всякое составное число может быть единственным образом представлено в виде произведения простых множителей. Например,

48 = 2 · 2 · 2 · 2 · 3, 225 = 3 · 3 · 5 · 5, 1050 = 2 · 3 · 5 · 5 · 7 .

Для небольших чисел это разложение легко делается на основе таблицы умножения. Для больших чисел рекомендуем пользоваться следующим способом, который рассмотрим на конкретном примере. Разложим на простые множители число 1463. Для этого воспользуемся таблицей простых чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,

47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101,

103, 107, 109, 113, 127, 131, 137, 139, 149, 151,

157, 163, 167, 173, 179, 181, 191, 193, 197, 199.

Перебираем числа по этой таблице и останавливаемся на том числе, которое является делителем данного числа. В нашем примере это 7. Делим 1463 на 7 и получаем 209. Теперь повторяем процесс перебора простых чисел для 209 и останавливаемся на числе 11, которое является его делителем (см. параграф «Признаки делимости»). Делим 209 на 11 и получаем 19, которое в соответствии с этой же таблицей является простым числом. Таким образом, имеем: 1463 = 7 ∙ 11 ∙ 19, т.е. простыми делителями числа 1463 являются 7, 11 и 19. Описанный процесс можно записать следующим образом:

Признаки делимости

Признаки делимости

Признаки делимости на 2, 4, 8, 3, 9, 6, 5, 25, 10, 100, 1000, 11.

Признак делимости на 2. Число делится на 2, если его последняя цифра — ноль или делится на 2. Числа, делящиеся на два, называются чётными, не делящиеся на два – нечётными.

Признак делимости на 4. Число делится на 4, если две егопоследние цифры — нули или образуют число, которое делится на 4.

Признак делимости на 8. Число делится на 8, если три егопоследние цифры — нули или образуют число, которое делится на 8.

Признаки делимости на 3 и 9. Число делится на 3, если егосумма цифр делится на 3. Число делится на 9, если его сумма цифр делится на 9.

Признак делимости на 6. Число делится на 6, если оно делится на 2 и на 3.

Признак делимости на 5. Число делится на 5, если его последняя цифра — ноль или 5.

Признак делимости на 25. Число делится на 25, если две егопоследние цифры — нули или образуют число, которое делится на 25.

Признак делимости на 10. Число делится на 10, если егопоследняя цифра — ноль.

Признак делимости на 100. Число делится на 100, если две егопоследние цифры – нули.

Признак делимости на 1000. Число делится на 1000, если триего последние цифры – нули.

Признак делимости на 11. На 11 делятся только те числа, у которых сумма цифр, стоящих на нечётных местах, либо равна сумме цифр, стоящих на чётных местах, либо отличается от неё на число, делящееся на 11.

Существуют признаки делимости и для некоторых других чисел, однако они более сложные и в программе средней школы не рассматриваются.

П р и м е р . Число 378015 делится на 3, так как сумма его цифр равна:

3 + 7 + 8 + 0 + 1 + 5 = 24, а это число делится на 3. Данное

число делится на 5, так как его последняя цифра 5. Наконец,

это число делится на 11, так как суммы его нечётных цифр:

3 + 8 + 1 = 12 и чётных цифр 7 + 0 + 5 = 12 равны.

Но это число не делится на 2, 4, 6, 8, 9, 10, 25, 100 и 1000, так как …

Источник

НОД, НОД

НОД — это наибольший общий делитель.

НОК — это наименьшее общее кратное.

Определения:

1. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
2. Наименьшее общее кратное (НОК) двух целых чисел m и n есть наименьшее натуральное число, которое делится на m и n без остатка

Способы нахождения НОД двух чисел:

1 способ (следует из определения): Метод полного перебора для нахождения наибольшего общего делителя (НОД)  натуральных чисел.

1. Выписываем все делители числа а;
2. Выписываем все делители числа b;
3. Выбираем среди них общие делители;
4. Среди общих делителей выбираем самое большое число – это и есть НОД(a, b).

2 способ : Метод перебора делителей меньшего числа для нахождения наибольшего общего делителя (НОД)  натуральных чисел.

1. Найти делители меньшего из данных чисел.
2. Найти, начиная с большего, тот из выписанных делителей, который является также делителем другого числа.
3. Записать найденное число – НОД.

3 способ; Метод нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью разложения на множители.

1. Находим разложение чисел на простые множители.
2. Подчеркиваем общие числа.
3. Находим произведение подчеркнутых чисел у одного числа.
4. Записываем ответ.

4 способ: Алгоритм Евклида нахождения наибольшего общего делителя (НОД)  двух натуральных чисел вычитанием.

1. Из большего числа вычитается меньшее.
2. Если получается 0, то числа равны друг другу и являются наибольшим общим делителем.
3. Если результат вычитания не равен 0, то большее число заменяется на результат вычитания.
4. Переход к пункту 1.

Способы нахождения НОК двух чисел:

1 способ: Метод перебора
1.    Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.

2 способ; Метод нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью разложения на множители

1.  Разложить данные числа на простые множители.
2.  Выписать в строчку множители, входящие в разложение самого большого из чисел, а под ним – разложение остальных чисел.
3.  Подчеркнуть в разложении меньшего числа множители, которые не вошли в разложение бóльшего числа и добавить эти множители в разложение большего числа. 
4.  Полученное произведение записать в ответ. 

    Свойства наибольшего общего делителя:

1. НОД(a, b) = НОД(b, a)
2. НОД(a, b) = НОД(-a, b)
3. НОД(a, b) = НОД(|a|,|b|)
4. НОД(a, 0) = |a|
5. НОД(a, к • a) = |a|, при любом к ∈ Z
6. НОД(a, НОД(b, с)) = НОД(НОД(a, b), c)

Свойства наименьшего общего кратного:

1. НОК(a, b) = НОК(b, a)
2. НОД(a, b) = НОД(-a, b)
3. НОД(a, b) = НОД(|a|,|b|)
4. НОК(a, НОК(b, с)) = НОК(НОК(a, b), c)