Как найти наибольший обьем

Помогаю со студенческими работами здесь

Найти объем цилиндра
В цилиндре параллельно его оси на расстоянии 4 см от нее проведено сечение, диагональ которого…

Объем цилиндра равен V, а площадь основания – S. Какова высота цилиндра Н?
Написать программу, которая вычисляет Объем цилиндра равен V, а площадь основания – S. Какова…

Вычислить площадь боковой поверхности цилиндра, если известны высота h см и объем V cм3 цилиндра.
Вычислить площадь боковой поверхности цилиндра,если известны высота h см и объем V cм3 цилиндра.

Найти объем конуса / цилиндра
добрый день! помогите решить пожалуйста 2 задачи по геометрии. сам геометрию не очень хорошо знаю….

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

1. шаг – записываем формулу площади (объема) (S=a*b).
2. шаг – выражаем одну сторону фигуры через другую. Например в задаче “Проволока длинной 76 см согнута в прямоугольник , найдите длину сторон, при которых площадь прямоугольника наибольшая” была указана связь между сторонами прямоугольника – известный периметр, что позволило выразить одну сторону через другую и периметр (b  = frac{P}{2}-a)), аналогично и в задаче Периметр основания прямоугольного параллелепипеда  .
3. шаг – подставляем подученную формулу в формулу порщади (объема)(например для прямоугольника (S=a*b = a*(frac{P}{2}-a) = a*frac{P}{2}-a^2).
4. шаг – находим первую производную и приравниваем ее к нулю (S’= (a*frac{P}{2}-a^2)` = frac{P}{2}-2*a = 0)
5. шаг – решаем полученное уравнение и находим корни уравнения (т.е. значения неизвестного при котором значение функции (производной) равно 0). Это и будет ответ, т.е. длина стороны при которой площадь будет наибольшей (аналогично и с объемом) (frac{P}{2}-2*a = 0 => a = frac{P}{4}).
6. шаг – желательно проверить истинность полученного решения – подставить найденное значение в функцию (площади или объема) и рассчитать ее, а для сравнения взять соседнее значение стороны (больше или меньше) и так же подставить. Если площадь получится меньше, значит задача решена верно, если нет, то нужно искать ошибку.

P.S. вопросы и пожелания пишите в личку.

Пифагор: h^2=l^2-r^2, где ^ – степень, r – радиус основания.

Объём конуса: V=1/3*pi*r^2*koren(l^2-r^2).

Обозначим для удобства x=r^2, x > 0.
Объём наибольший, когда функция y(x)=x*koren(l^2-x) имеет наибольшее значение. При этом f(x)=x^2*(l^2-x) тоже будет максимально.

Приравниваем к 0 производную:

(x^2*l^2-x^3)’=0, 2x*l^2-3x^2=0, x=2/3*l^2.

Итак, максимальный объем при r^2=2/3*l^2.
Осталось подставить это в формулу для V.

Анастасия СерыхУченик (88)

8 лет назад

“Объём наибольший, когда функция y(x)=x*koren(l^2-x)”-а куда делось 1/3pi?

Alexander Alenitsyn
Высший разум
(754323)
Функция у (х) отличается от объема только постоянным множителем, поэтому значение х, при котором объём максимальный, то же самое, при котором у (х) максимальна.

0 Пользователей и 1 Гость просматривают эту тему.

---

---

МЕТОДИЧЕСКАЯ ИНФОРМАЦИЯ

Название образовательной программы

Авторская  программа курса информатики и информационных технологий для 5-7 классов лицея № 4 г. Краснодара Коротенко А. А, разработанная на основе обязательного минимума содержания образования по информатике (уровень Б) и учебного плана  МОУ-лицей  № 4 города Краснодар.

Тип урока

Практическая работа: «Определение наибольшего объема коробки» по теме «Компьютерные модели» для учащихся 6 класса

Цели урока

Обучающая – научить анализировать текст задачи, разбивать решение задачи на этапы, применять на практике полученные знания, научить проводить компьютерный эксперимент, использовать для решения задачи графики и диаграммы. 

Развивающая – учить анализировать полученные результаты, сравнивать, делать выводы.

Воспитательная – воспитывать творческий подход к труду, аккуратность, ответственность.

Задачи урока

• Выполнить постановку задачи «Определение наибольшего объема коробки».
• Разработать математическую модель решения.
• Выполнить компьютерную реализацию модели.
• Провести компьютерный эксперимент.
• Проанализировать  результаты и  сделать выводы.

Ожидаемые результаты

В ходе урока ученики актуализируют знания, приобретенные при изучении тем «Моделирование», «Компьютерное моделирование», приобретут практические навыки в решении задачи путем разбиения процесса решения на этапы, в том числе: в проведении компьютерного эксперимента  и анализе полученных результатов, закрепят знания о назначении, целесообразности и смысле  компьютерного моделирования.

ПОДРОБНЫЙ КОНСПЕКТ УРОКА

 Мотивация учащихся

Раздел  «Моделирование»  является интересным, но непростым  для понимания и усвоения в школьном курсе информатики.  Рассматриваемый  урок является логическим продолжением  изучения теоретического материала по теме  «Компьютерное моделирование»    и  содержит  Практическую работу,  назначение которой: в процессе решения несложной задачи  рассмотреть все этапы построения и применения компьютерной  модели  и добиться от каждого ученика полного выполнения и усвоения предложенного материала.

Цель решения задачи доступна для понимания учащимися 6 класса. Математическая модель решения задачи знакома учащимся из курса математики. Во время объяснения учитель использует  презентацию, которая содержит цель работы, повторение необходимого теоретического материала, задание на текущий урок, домашнее задание. Учитель организует совместное обсуждение работы с учащимися в форме диалога. На этапе формализации и постановки задачи применяется раздаточный материал – бумажные модели (развертки) прямоугольных параллелепипедов,  выполненные  из квадрата заданного размера, но с различной величиной выреза для того, чтобы учащиеся могли убедиться и самостоятельно обосновать необходимость применения компьютерного моделирования.

Учащиеся понимают, что цель урока – создать компьютерную модель, провести эксперимент и проанализировать результаты. Для большей наглядности можно использовать графики и диаграммы. Результаты трех компьютерных экспериментов учащиеся будут заносить в таблицу.

Ход и содержание урока

I. Объявление темы, целей и задач урока

II. Актуализация опорных знаний

Учитель предлагает ученикам вспомнить, что такое моделирование и модель, виды моделей. Повторить понятия формализации, обсудить: какая задача считается «хорошо поставленной»? Учащиеся повторяют этапы решения задачи на компьютере. Раскрывают понятие «адекватности модели». Учитель подводит учеников к выводу о том, что существуют ситуации, когда компьютерное моделирование является единственно возможным способом решения поставленной задачи.

III. Объяснение содержания и выполнение практической работы – презентация

Сформулируем задачу. Из квадратного листа металла необходимо сделать коробку наибольшего объема. [1]

Некоторые из вас, ребята, ошибочно полагают, что какую бы форму не имела коробка, сделанная из одного и того же листа, её объём будет постоянным. От чего же зависит объём коробки? Можем ли мы позволить себе взять несколько листов металла и наугад выкраивать коробки? Каким образом мы убедимся, что полученная коробка будет иметь наибольший объём? Очевидно, что нам поможет компьютерное моделирование.

Этап 1. Постановка задачи

Дано: квадрат со стороной  а см. По углам вырезаются квадраты со стороной b см. Найти: величину выреза b такую, чтобы объем коробки был наибольшим.

Этап 2.  Построение математической модели

Нам необходимо найти объем прямоугольного параллелепипеда. Воспользуемся известной формулой   V=a*b*c. Заметим, что в качестве расчетной формулы мы могли бы использовать другие алгебраические выражения, но  была бы при этом модель адекватной? Доработаем модель. Длина и ширина нашей коробки равны с см, а высота равна b см, поэтому формула для вычисления объема прямоугольного параллелепипеда примет вид  V=b*c*с.

Выразим с через а и b: с=а-2*b

Математическая модель для решения нашей задачи построена.

Этап 3.  Компьютерная реализация  модели

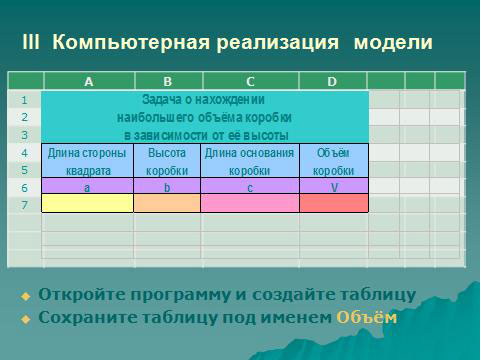
Откройте табличный процессор и создайте таблицу. Сохраните таблицу под именем Объём. В ячейке А7 будем хранить длину стороны квадрата. Эта величина не меняется в процессе решения задачи.

В столбец В, начиная с ячейки В7, будем записывать высоту коробки. Начальное значение высоты – о см. Эта величина будет нарастать с заданным шагом. В столбце С, начиная с ячейки С7, будем вычислять длину основания коробки в зависимости от величины выреза по формуле  с=а-2*b. Переведём эту формулу на язык табличного  процессора, предварительно  вспомнив: «Какая величина в процессе решения задачи  не меняется?» Остаётся постоянной длина стороны листа, поэтому   формула имеет вид:   =А$7-2*В7. В столбце D будем вычислять объём коробки по формуле V=b*c*с. В ячейку D7 самостоятельно запишем соответствующую формулу. Формула имеет вид:  =В7*С7*С7   или    =В7*СТЕПЕНЬ(С7;2). Выполните копирование формул в столбцах С и D. Построение компьютерной модели решения задачи завершено.

Этап 4. Компьютерный эксперимент

Приступим к самой интересной части нашей работы. Пусть длина стороны квадратного листа равна 1м или 100 см. Будем постепенно увеличивать высоту коробки (величину выреза) для того, чтобы найти наибольший объём. Высоту коробки будем менять, задавая шаг. Подготовьте таблицу для записи результатов эксперимента. В графу «Величина выреза» запишите простым карандашом предполагаемые ответы – высоту коробки. После окончания эксперимента, у нас появится возможность сравнить Ваш прогноз и результаты расчетов. В ячейку В7 запишем начальное значение величины  выреза – 0 см. В ячейку В8 запишем величину шага – 1 см. Выделите эти две ячейки и выполните автоматическое заполнение следующих за ними ячеек. Как называется полученный ряд чисел? Арифметическая прогрессия с разностью 1.

Проанализируем полученные результаты. Очевидно, что ответ находится в строке номер 24. При величине выреза 17 см наибольший объём равен 74052 куб.см.

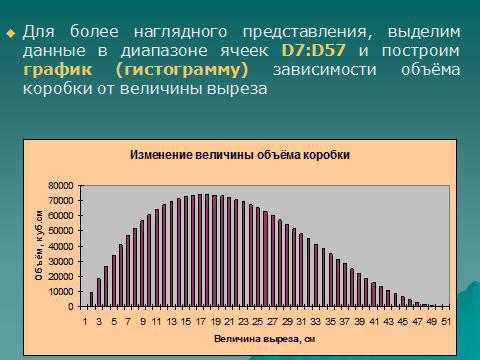
Для более наглядного представления, выделим данные в диапазоне ячеек D7:D57 и построим график (гистограмму) зависимости объёма коробки от величины выреза. Продолжим эксперимент. Изменим величину шага. В ячейку В8 внесём  2 см. Выделите ячейки В7 и В8 и выполните автоматическое заполнение следующих за ними ячеек. Какой теперь вы получили результат? Сравните новый результат с предыдущим. При величине выреза 16 см наибольший объём равен 73984 куб.см. Занесите результаты двух экспериментов в таблицу. Какие можно сделать выводы?

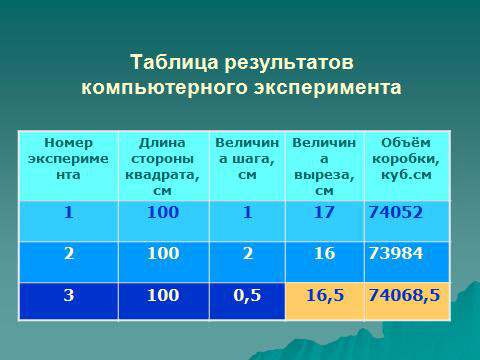
Проведём заключительный опыт. Уменьшим величину шага. В ячейку В8 запишем число 0,5.  Занесите результат в таблицу ответов:  При величине выреза 16,5 см наибольший объём равен 74068,5 куб.см.

Этап 5. Анализ результатов

Проанализируйте полученные результаты и в рабочей тетради сделайте краткие выводы.

Ответьте на вопросы.

1. Возможно ли проведение большего количества опытов?
2. Является ли наш «наилучший» результат окончательным?
3. Можно ли признать полученный нами результат удовлетворительным и почему?
4. Сравните результаты компьютерного моделирования с предполагаемыми ответами.

IV.  Физкультминутка

V. Обсуждение пройденного материала и подведение итогов урока. Результатом решения задачи является вывод о том, что по итогам проведенных опытов наибольший объём коробки равен 74068,5 куб.см. при величине выреза 16,5 см.

VI. Домашнее задание. Учащимся выдаются карточки с домашним заданием.

ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ

Использование презентации и средств мультимедиа

После объявления темы, целей и задач урока  на этапе мотивации учебной деятельности и актуализации знаний учащихся предполагается обращение  к презентации. Учитель  демонстрирует этапы решения задачи, объясняет содержание экспериментов, указывает способ  записи промежуточных результатов и вывода. Ученики  включаются в обсуждение предстоящей работы, после чего приступают к выполнению задания.

В презентации представлено полное содержание практической работы. Это цели и задачи урока, повторение теоретического материала,  формулировка  решаемой задачи, рисунки, схемы, все этапы решения, содержание и результаты экспериментов, таблицы, графики, домашнее задание с подробным решением.

Поэтому, проводя  урок, учитель может использовать всю презентацию или ее фрагменты, увеличивать или уменьшать число экспериментов, применять раздаточный материал: таблицы для занесения результатов опытов, карточки с домашним заданием.

Сcылка для скачивания презентации: http://edu.letitbit.net

При  изучении данной темы, целесообразно использовать  средства  мультимедиа, так как именно это позволяет ученику за малый промежуток времени охватить взглядом весь урок, понять смысл предстоящей работы и предполагаемый результат, то есть выстроить четкую картину действий. Этому особенно способствуют наглядные объекты – чертежи, схемы, графики, диаграммы, таблицы.

Все изложенное выше приводит к успешному решению поставленной задачи.

Вопросы для устной работы на этапе актуализации опорных знаний

• Моделирование – это замена одного объекта (процесса или явления) другим, при условии схранения всех существенных свойств исходного объекта (процесса или явления)
• Модель – это заменяющий объект (процесс или явление) Приведите примеры объектов, процессов и явлений и их моделей.
• Приведите примеры существенных и несущественных свойств одного и того же объекта, процесса или явления
• Виды моделей: наглядные и информационные
• Информационная модель – это модель, представляющая объект (процесс или явление) набором параметров и связей между ними
• Основным языком информационного моделирования является язык математики
• Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями
• Процесс описания факторов модели с помощью параметров называется формализацией
• Умение «хорошо поставить задачу», т.е. построить модель, учитывающую все существенные факторы, является искусством построения модели
• Модель называется адекватной, если при испытаниях она даёт удовлетворительные результаты
• Приведите пример такой ситуации, когда компьютерное моделирование является единственно возможным способом решения поставленной задачи[3]

Проверка и оценивание ЗУНов

Учитель оценивает наиболее полные и точные ответы учащихся во время устной работы, а также проверяет и оценивает результат решения задачи, оформленный в виде кратких выводов в  тетради. А именно: результаты компьютерных экспериментов, их анализ,  выводы о величине выреза – высоте коробке, при заданной длине стороны квадратного листа, такой, чтобы ее объем был наибольшим.

Карточки с домашним заданием

Постройте математические модели для приведенных ниже задач. Сравните полученные модели. Запишите выводы.

Задача 1. Первая труба наполняет бассейн за а минут, а вторая – за b минут. За какое время обе трубы наполнят бассейн, работая одновременно?[2]

Задача 2. Два теплохода одновременно отошли от разных пристаней и направились по озеру навстречу друг другу. Первый теплоход преодолевает все расстояние за c часов,  а второй – за d часов. Через сколько часов теплоходы встретятся?[2]

Решите задачу с помощью электронных таблиц,  используя приведенную ниже  математическую модель.

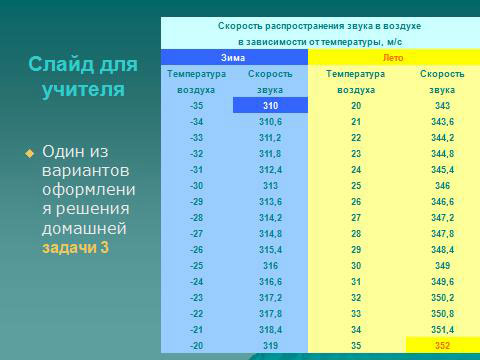
Задача 3. Скорость  распространения звука в воздухе в зависимости от температуры может быть найдена приближенно по формуле v=331+0,6t, где v – скорость (в метрах в секунду), t – температура (в градусах Цельсия).  Найдите, с какой скоростью распространяется звук зимой при температуре воздуха от -35˚С до -20˚ С и летом при температуре воздуха от 20˚ С до 35˚.[2]

Логический переход от данного урока к последующим

Представленный урок является первой Практической работой  из серии работ по теме  «Компьютерное моделирование». В процессе решения несложной задачи  необходимо было рассмотреть все этапы построения и применения компьютерной  модели.  

Далее мы переходим к решению задач  «Прирост массы растений»,  отрабатывая «Модель неограниченного роста», «Модель ограниченного роста», «Модель потребления возобновляемых ресурсов»[3], адаптированные  для учащихся 6 класса.

В результате завершения работ по всему циклу и  опираясь на результаты компьютерного моделирования,  дети с большим удовольствием отвечают на вопрос: «Сколько можно брать у живой природы, чтобы ее запасы не истощались?», что само по себе имеет большое воспитательное значение, акцентирует внимание детей на бережном отношении к окружающей среде и находит отклик в душах детей среднего школьного возраста.

Для оформления уроков выбраны картинки живой природы с целью придания единого смысла всем практическим работам, логическим завершением которых являются задачи о разумном подходе к потреблению природных ресурсов.

Список литературы

1. Н. В. Макарова  «Информатика 7–9  задачник по моделированию», Санкт-Петербург, Питер, 2001
2. Л.Л. Босова, В. В. Трофимова, А. Ю. Босова «Изучаем информационные технологии в 7 классе: информационное моделирование», «Информатика в школе», Москва, Образование и информатика, 2007
3. А. Г. Гейн, А.Н.Сенокосов,  Н. А. Юнерман «Информатика 10–11», Москва, Просвещение, 2004