Найдите наибольший отрицательный корень уравнения
Дата: 2018-02-02
14840
Категория: Простейшие уравнения
Метка: ЕГЭ-№5
Найдите наибольший отрицательный корень уравнения:
Решением уравнения cosx=a являются два корня:
Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от –2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: –3 и 3, –4 и 4 и так далее. Вычисляем:
При n = – 2 х1= 3(– 2) – 4,5 = – 10,5 х2= 3(– 2) – 5,5 = – 11,5
При n = – 1 х1= 3(– 1) – 4,5 = – 7,5 х2= 3(– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
Ответ: –1,5
Найдите наименьший положительный корень уравнения:
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от –90о до 90о синус которого равен a.
Значит
Выразим x (умножим на 4 и разделим на Пи):
Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n получим отрицательные корни. Поэтому будем подставлять n=0,1,2 …
При n = 0 х = (– 1)0 + 4∙0 + 3 = 4
При n = 1 х = (– 1)1 + 4∙1 + 3 = 6
При n = 2 х = (– 1)2 + 4∙2 + 3 = 12
Проверим при n=–1 х=(–1)–1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
Ответ: 4
Найдите наименьший положительный корень уравнения:
Решением уравнения tg x = a является корень:
Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90о до 90о, тангенс которого равен a.
Значит
Выразим x (умножим на 6 и разделим на Пи):
Найдём наименьший положительный корень. Подставим значения n=0,1,2,3 … Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:
Таким образом, наименьший положительный корень равен 0,25.
Ответ: 0,25
Найдите наибольший отрицательный корень уравнения
Найдите наибольший отрицательный корень уравнения:
Решением уравнения cosx=a являются два корня:
Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от –2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: –3 и 3, –4 и 4 и так далее. Вычисляем:
При n = – 2 х1= 3 (– 2) – 4,5 = – 10,5 х2= 3 (– 2) – 5,5 = – 11,5
При n = – 1 х1= 3 (– 1) – 4,5 = – 7,5 х2= 3 (– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
Найдите наименьший положительный корень уравнения:
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от –90 о до 90 о синус которого равен a.
Значит
Выразим x (умножим на 4 и разделим на Пи):
Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n получим отрицательные корни. Поэтому будем подставлять n=0,1,2 …
При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4
При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6
При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12
Проверим при n=–1 х=(–1) –1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
Найдите наименьший положительный корень уравнения:
Решением уравнения tg x = a является корень:
Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90 о до 90 о , тангенс которого равен a.
Значит
Выразим x (умножим на 6 и разделим на Пи):
Найдём наименьший положительный корень. Подставим значения n=0,1,2,3 … Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:
Таким образом, наименьший положительный корень равен 0,25.
Тригонометрические уравнения
Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно. Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.
В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.
Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.
Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.
Понимание раздела «Тригонометрия» в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.
В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:
Знание этих значений необходимо, это «азбука», без которой невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да просто вы именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.
Алгоритм восстановления этих значений прост, он также приведён в теории, полученной вами во втором письме после подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».
Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с использованием угла х для соответствующих уравнений: cosx=a, sinx=a, tgx=a, где х может быть и выражением. В примерах ниже у нас аргумент задан именно выражением.
Итак, рассмотрим следующие задачи:
Найдите корень уравнения:
В ответе запишите наибольший отрицательный корень.
Решением уравнения cos x = a являются два корня:
Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от – 2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: – 3 и 3, – 4 и 4 и так далее.
При n = – 2 х1= 3 (– 2) – 4,5 = – 10,5 х2= 3 (– 2) – 5,5 = – 11,5
При n = – 1 х1= 3 (– 1) – 4,5 = – 7,5 х2= 3 (– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
В ответе напишите наименьший положительный корень.
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от – 90 о до 90 о синус которого равен a.
Выразим x (умножим обе части уравнения на 4 и разделим на Пи):
Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n = 0,1,2 …
При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4
При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6
При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12
Проверим при n = –1 х = (–1) –1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
В ответе напишите наименьший положительный корень.
Решением уравнения tg x = a является корень:
Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90 о до 90 о , тангенс которого равен a.
Выразим x (умножим обе части уравнения на 6 и разделим на Пи):
Найдём наименьший положительный корень. Подставим значения n = 1,2,3. Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:
Таким образом, наименьший положительный корень равен 0,25.
Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.
Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если в ходе решения вы не сможете определить угол, например, для
то данные формулы вам помогут:
Спасибо за внимание, учитесь с удовольствием!
Тригонометрические уравнения. Как решать тригонометрические уравнения?
Тригонометрические уравнения – уравнения, содержащие переменную под знаком тригонометрических функций.
Если проще: это уравнения, в которых неизвестные (иксы) или выражения с ними находятся внутри синусов , косинусов , тангенсов и котангенсов .
Как решать тригонометрические уравнения:
Любое тригонометрическое уравнение нужно стремиться свести к одному из видов:
где (t) – выражение с иксом, (a) – число. Такие тригонометрические уравнения называются простейшими. Их легко решать с помощью числовой окружности ( тригонометрического круга ) или специальных формул:
(sin x=a) (⇔) ( left[ beginx=arcsin a+2πn, n∈Z\ x=π-arcsin a+2πl, l∈Zendright.)
если (a∈[-1;1])
Инфографику о решении простейших тригонометрических уравнений смотри здесь: (sinx=a) , (cosx=a) , (tgx=a) и (ctgx=a) .
Пример. Решите тригонометрическое уравнение (sinx=-)(frac<1><2>).
Решение:
Решим уравнение с помощью числовой окружности. Для этого:
1) Построим оси.
2) Построим окружность.
3) На оси синусов (оси (y)) отметим точку (-) (frac<1><2>) .
4) Проведем перпендикуляр к оси синусов через эту точку.
5) Отметим точки пересечения перпендикуляра и окружности.
6)Подпишем значения этих точек: (-) (frac<π><6>) ,(-) (frac<5π><6>) .
7) Запишем все значения соответствующие этим точкам с помощью формулы (x=t+2πk), (k∈Z):
(x=-) (frac<π><6>) (+2πk), (k∈Z); (x=-) (frac<5π><6>) (+2πn), (n∈Z)
Что означает каждый символ в формуле корней тригонометрических уравнений смотри в видео .
Внимание! Уравнения (sinx=a) и (cosx=a) не имеют решений, если (a ϵ (-∞;-1)∪(1;∞)). Потому что синус и косинус при любых икс больше или равны (-1) и меньше или равны (1):
Пример. Решить уравнение (cosx=-1,1).
Решение: (-1,1 (frac<π><4>) , (frac<5π><4>)
7) Запишем все значения этих точек. Так как они находятся друг от друга на расстоянии ровно в (π), то все значения можно записать одной формулой:
Ответ: (x=) (frac<π><4>) (+πk), (k∈Z).
Пример. Решите тригонометрическое уравнение (cos(3x+frac<π><4>)=0).
Решение:
Опять воспользуемся числовой окружностью.
1) Построим окружность, оси (x) и (y).
2) На оси косинусов (ось (x)) отметим (0).
3) Проведем перпендикуляр к оси косинусов через эту точку.
4) Отметим точки пересечения перпендикуляра и окружности.
5) Подпишем значения этих точек: (-) (frac<π><2>),(frac<π><2>) .
6)Выпишем все значение этих точек и приравняем их к аргументу косинуса (к тому что внутри косинуса).
7) Дальше решать в таком виде несколько трудновато, разобьем уравнение на два.
8) Как обычно в уравнениях будем выражать (x).
Не забывайте относиться к числам с (π), так же к (1), (2), (frac<1><4>) и т.п. Это такие же числа, как и все остальные. Никакой числовой дискриминации!
Ответ: (x=) (frac<π><12>) (+) (frac<2πk><3>) (x=-) (frac<π><4>) (+) (frac<2πk><3>) , (k∈Z).
Сводить тригонометрические уравнения к простейшим – задача творческая, тут нужно использовать и тригонометрические формулы , и особые методы решений уравнений:
– Метод введения новой переменной (самый популярный в ЕГЭ).
– Метод разложения на множители .
– Метод вспомогательных аргументов.
Рассмотрим пример решения квадратно-тригонометрического уравнения
Пример. Решите тригонометрическое уравнение (2cos^2x-5cosx+2=0)
Решение:
Сделаем замену (t=cosx).
Наше уравнение превратилось в типичное квадратное . Можно его решить с помощью дискриминанта .
(D=25-4 cdot 2 cdot 2=25-16=9)
Делаем обратную замену.
Первое уравнение решаем с помощью числовой окружности.
Второе уравнение не имеет решений т.к. (cosx∈[-1;1]) и двум быть равен не может ни при каких иксах.
Запишем все числа, лежащие на числовой окружности в этих точках.
Ответ: (x=±) (frac<π><3>) (+2πk), (k∈Z).
Пример решения тригонометрического уравнения с исследованием ОДЗ:
Пример(ЕГЭ). Решите тригонометрическое уравнение (frac<2cos^2x-sin<2x>>) (=0)
Есть дробь и есть котангенс – значит надо записать ОДЗ . Напомню, что котангенс это фактически дробь:
Потому ОДЗ для ctg(x): (sinx≠0).
Отметим «нерешения» на числовой окружности.
[spoiler title=”источники:”]
http://matematikalegko.ru/uravnenia/trigonometricheskie-uravneniya.html
http://cos-cos.ru/math/93/
[/spoiler]
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Тригонометрические уравнения
Тригонометрическое уравнение – уравнение, содержащее переменную (x) в аргументе одной или нескольких тригонометрических функций: синус, косинус, тангенс, котангенс.
(bullet) Стандартные тригонометрические уравнения:
[begin{array}{l|c|c}
hline text{Уравнение} & text{Ограничения} & text{Решение}\
hline &&\
sin x=a & -1leq aleq 1 & left[
begin{gathered}
begin{aligned}
&x=arcsin a+2pi n\
&x=pi -arcsin a+2pi m
end{aligned}
end{gathered}
right. , n,min mathbb{Z}\&&\
hline &&\
cos x=a & -1leq aleq 1 & x=pm arccos a+2pi n, nin
mathbb{Z}\&&\
hline &&\
mathrm{tg}, x=a & ain mathbb{R} & x=mathrm{arctg}, a+pi n,
nin
mathbb{Z}\&&\
hline &&\
mathrm{ctg},x=a & ain mathbb{R} & x=mathrm{arcctg}, a+pi n,
nin
mathbb{Z}\&&\
hline
end{array}]
(bullet) Таблица синусов, косинусов, тангенсов и котангенсов:
[{large{begin{array}{|c|c|c|c|c|c|}
hline &&&&&\[-17pt]
& quad 0 quad (0^ circ)& quad dfrac{pi}6 quad (30^circ)
& quad dfrac{pi}4
quad (45^circ) & quad dfrac{pi}3 quad (60^circ)& quad dfrac{pi}2 quad
(90^circ) \
&&&&&\[-17pt]
hline sin & 0 ½&frac{sqrt2}2&frac{sqrt3}2&1\[4pt]
hline cos &1&frac{sqrt3}2&frac{sqrt2}2½&0\[4pt]
hline mathrm{tg} &0 &frac{sqrt3}3&1&sqrt3&infty\[4pt]
hline mathrm{ctg} &infty &sqrt3&1&frac{sqrt3}3&0\[4pt]
hline
end{array}}}]
(bullet) Основные формулы приведения:
[begin{aligned}
&sin left(dfrac{pi}2pm xright)=cos x\[2pt]
&sin (pipm x)=mp sin x\[2pt]
&cos left(dfrac{pi}2 pm xright)=pm sin x\[2pt]
&cos(pi pm x)=-cos x
end{aligned}]
Формулы приведения для тангенса и котангенса легко вывести, зная, что [mathrm{tg},x=dfrac{sin x}{cos x} quad text{и} quad mathrm{ctg},x=
dfrac{cos x}{sin x}]
(bullet) Четность косинуса и нечетность синуса, тангенса и котангенса:
[begin{aligned}
cos(-x)&=cos x\
sin (-x)&=-sin x\
mathrm{tg},(-x)&=-mathrm{tg},x\
mathrm{ctg},(-x)&=-mathrm{ctg},x
end{aligned}]
Задание
1
#2786
Уровень задания: Равен ЕГЭ
Решите уравнение [sin alpha=1]
В ответе укажите наименьший положительный корень уравнения, деленный на (pi).
Данное уравнение равносильно серии корней [alpha=dfrac{pi}2+2pi
n,qquad ninmathbb{Z}.] Найдем положительные корни уравнения, решив неравенство: [dfrac{pi}2+2pi n>0quadLeftrightarrowquad n>-dfrac14
quadRightarrow] наименьшее подходящее целое (n) — это (n=0), при котором получается (alpha=dfrac{pi}2).
Следовательно, в ответ пойдет [dfrac{pi}2divpi=dfrac12=0,5.]
Ответ: 0,5
Задание
2
#2785
Уровень задания: Равен ЕГЭ
Решите уравнение [sin y=0]
В ответе укажите целый корень уравнения.
Данное уравнение равносильно серии корней [y=pi n, qquad
ninmathbb{Z}.] Заметим, что единственный целый корень из этой серии получается при (n=0) и это (y=0) (все остальные корни будут вида целое число умножить на (pi), что является иррациональным числом).
Ответ: 0
Задание
3
#2793
Уровень задания: Равен ЕГЭ
Решите уравнение [mathrm{ctg}, pi x=0]
В ответе укажите наименьший положительный корень.
Данное уравнение равносильно [pi x=dfrac{pi}2+pi
nquadLeftrightarrowquad x=dfrac12+n, quad ninmathbb{Z}.] Найдем положительный корень, решив неравенство [dfrac12+n>0quadLeftrightarrowquad n>-dfrac12quadRightarrow] наименьшее (n=0), откуда (x=dfrac12).
Ответ: 0,5
Задание
4
#2791
Уровень задания: Равен ЕГЭ
Решите уравнение [mathrm{tg}, dfrac x6=sqrt3]
В ответе укажите наименьший корень, принадлежащий отрезку ([0;2pi]), деленный на (pi).
Данное уравнение равносильно [dfrac x6=dfrac{pi}3+pi
nquadLeftrightarrowquad x=2pi+6pi n, qquad ninmathbb{Z}.] Корни, принадлежащие отрезку ([0;2pi]), найдем, решив неравенство: [0leqslant 2pi+6pi nleqslant 2piquadLeftrightarrowquad
-dfrac13leqslant nleqslant 0] Целое (n), принадлежащее отрезку (left[-frac13;0right]), это (n=0). Следовательно, корень (x=2pi). Следовательно, в ответ пойдет (2).
Ответ: 2
Задание
5
#2792
Уровень задания: Равен ЕГЭ
Решите уравнение [sin x=dfrac{sqrt2}2]
В ответе укажите наименьший положительный корень, принадлежащий первой четверти, деленный на (pi).
Данное уравнение равносильно [x_1=dfrac{pi}4+2pi nquad
{small{text{и}}} quad x_2=dfrac{3pi}4+2pi m,quad
n,minmathbb{Z}.]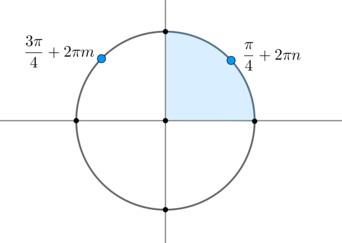
Видим, что в первой четверти лежит только серия (x_1=dfrac{pi}4+2pi n). Найдем наименьший положительный корень, решив неравенство: [dfrac{pi}4+2pi n>0 quadLeftrightarrowquad
n>-dfrac18 quadRightarrow] наименьшее целое (n=0), при котором получаем корень (x=dfrac{pi}4). Следовательно, в ответ запишем (dfrac{pi}4div pi=dfrac14=0,25.)
Ответ: 0,25
Задание
6
#443
Уровень задания: Равен ЕГЭ
Найдите корень уравнения [sin{biggl(dfrac{pi}{9} xbiggr)} = dfrac{1}{2}.] Если уравнение имеет более одного корня, в ответе укажите меньший из его положительных корней.
ОДЗ: (x) – произвольное. Решим на ОДЗ:
Решение уравнения (sin x = a) имеет вид: (x_1 = mathrm{arcsin}, a + 2pi n, x_2 = pi – mathrm{arcsin}, a + 2pi n, n in mathbb{Z}), откуда для исходного уравнения получаем [dfrac{pi}{9} x_1 = dfrac{pi}{6} + 2pi n, n in mathbb{Z}, qquad dfrac{pi}{9} x_2 = pi – dfrac{pi}{6} + 2pi n, n in mathbb{Z},] что равносильно (x_1 = 1,5 + 18n, n in mathbb{Z}), (x_2 = 7,5 + 18n, n in mathbb{Z}) – подходят по ОДЗ. Среди корней наименьший положительный (x = 1,5).
Ответ: 1,5
Задание
7
#2790
Уровень задания: Равен ЕГЭ
Решите уравнение [mathrm{tg}, dfrac x3=1]
В ответе укажите произведение наибольшего отрицательного и наименьшего положительного корней уравнения, деленное на (pi^2).
Данное уравнение равносильно [dfrac x3=dfrac{pi}4+pi
nquadLeftrightarrowquad x=dfrac{3pi}4+3pi n, qquad
ninmathbb{Z}.]
Найдем отрицательные корни уравнения, решив неравенство: [dfrac{3pi}4+3pi n<0quadLeftrightarrowquad
n<-dfrac14quadRightarrow] наибольший отрицательный корень получается при (n=-1) и это (x=-dfrac{9pi}4).
Найдем положительные корни уравнения, решив неравенство: [dfrac{3pi}4+3pi n>0quadLeftrightarrowquad
n>-dfrac14quadRightarrow] наибольший отрицательный корень получается при (n=0) и это (x=dfrac{3pi}4).
Тогда произведение, деленное на (pi^2), равно [-dfrac{9pi}4cdot dfrac{3pi}4divpi^2=-dfrac{27}{16}=-1,6875.]
Ответ: -1,6875
На этапе подготовки к ЕГЭ по математике старшеклассникам полезно повторить, как решать тригонометрические уравнения. Задания из данного раздела вызывают у учащихся определенные сложности, поэтому к ним необходимо отнестись с особым вниманием. Здесь вы можете ознакомиться с теорией, требующейся для выполнения упражнений, а также примерами с решениями тригонометрических уравнений. Обратите внимание, что подобные задания встречаются в аттестационных тестах довольно часто, поэтому пропускать повторение темы не стоит.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха!
С помощью нашего образовательного портала занятия по математике будут проходить легко, и даже одни из самых сложных уравнений не вызовут особых затруднений. На сайте «Школково» представлены все необходимые для успешной сдачи ЕГЭ материалы.
Вся основная информация по теме использования функций (синуса, косинуса, тангенса и котангенса) располагается в разделе «Теоретическая справка», куда вы можете перейти с помощью кнопки «Ознакомиться с полной теорией». Наши преподаватели систематизировали и изложили все необходимые для успешной сдачи материалы в максимально простой и понятной форме. Вы быстро найдете необходимые правило и формулу, и решение тригонометрических уравнений будет даваться максимально легко.
А в разделе «Каталоги» вы сможете попрактиковаться в выполнении заданий. Здесь вы найдете множество уравнений различной сложности, в том числе профильного уровня.
Если какое-либо задание вызвало у вас затруднения, его можно добавить в «Избранное» и вернуться к нему позже для повторения или обсуждения решения с преподавателем.
База «Школково» постоянно обновляется, поэтому недостатка в задачах не будет.
На нашем портале могут заниматься не только московские школьники, но и ученики из городов по всей России. Чтобы приступить к повторению данной темы, а также, например, решению логарифмических уравнений, зарегистрируйтесь на сайте shkolkovo.net. Для большей эффективности уроков рекомендуем ежедневные занятия на нашем портале.
УСТАЛ? Просто отдохни
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
1 мая
Бесплатные курсы подготовки к ЕГЭ и ОГЭ
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
|
|
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Тригонометрические уравнения
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 5 № 26669 
i
Найдите корни уравнения: 
В ответ запишите наибольший отрицательный корень.
Аналоги к заданию № 26669: 12891 12957 13173 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
2
Тип 5 № 77376
i
Решите уравнение 
В ответе напишите наибольший отрицательный корень.
Аналоги к заданию № 77376: 103025 103513 103515 … Все
Решение
·
Видеокурс
·
Помощь
3
Тип 5 № 77377
i
Решите уравнение 
В ответе напишите наименьший положительный корень.
Аналоги к заданию № 77377: 103525 104013 104015 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
|
||||||||||
|
||||||||||
