Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given a positive integer ‘n'( 1 <= n <= 1015). Find the largest prime factor of a number.
Input: 6 Output: 3 Explanation Prime factor of 6 are- 2, 3 Largest of them is '3' Input: 15 Output: 5
The approach is simple, just factorise the given number by dividing it with the divisor of a number and keep updating the maximum prime factor. See this to understand more.
C++
#include <iostream>
#include<bits/stdc++.h>
using namespace std;
long long maxPrimeFactors(long long n)
{
long long maxPrime = -1;
while (n % 2 == 0) {
maxPrime = 2;
n >>= 1;
}
while (n % 3 == 0) {
maxPrime = 3;
n=n/3;
}
for (int i = 5; i <= sqrt(n); i += 6) {
while (n % i == 0) {
maxPrime = i;
n = n / i;
}
while (n % (i+2) == 0) {
maxPrime = i+2;
n = n / (i+2);
}
}
if (n > 4)
maxPrime = n;
return maxPrime;
}
int main()
{
long long n = 15;
cout << maxPrimeFactors(n) << endl;
n = 25698751364526;
cout << maxPrimeFactors(n);
}
C
#include <math.h>
#include <stdio.h>
long long maxPrimeFactors(long long n)
{
long long maxPrime = -1;
while (n % 2 == 0) {
maxPrime = 2;
n >>= 1;
}
while (n % 3 == 0) {
maxPrime = 3;
n = n / 3;
}
for (int i = 5; i <= sqrt(n); i += 6) {
while (n % i == 0) {
maxPrime = i;
n = n / i;
}
while (n % (i + 2) == 0) {
maxPrime = i + 2;
n = n / (i + 2);
}
}
if (n > 4)
maxPrime = n;
return maxPrime;
}
int main()
{
long long n = 15;
printf("%lldn", maxPrimeFactors(n));
n = 25698751364526;
printf("%lld", maxPrimeFactors(n));
return 0;
}
Java
import java.io.*;
import java.util.*;
class GFG {
static long maxPrimeFactors(long n)
{
long maxPrime = -1;
while (n % 2 == 0) {
maxPrime = 2;
n >>= 1;
}
while (n % 3 == 0) {
maxPrime = 3;
n = n / 3;
}
for (int i = 5; i <= Math.sqrt(n); i += 6) {
while (n % i == 0) {
maxPrime = i;
n = n / i;
}
while (n % (i + 2) == 0) {
maxPrime = i + 2;
n = n / (i + 2);
}
}
if (n > 4)
maxPrime = n;
return maxPrime;
}
public static void main(String[] args)
{
Long n = 15l;
System.out.println(maxPrimeFactors(n));
n = 25698751364526l;
System.out.println(maxPrimeFactors(n));
}
}
Python3
import math
def maxPrimeFactors (n):
maxPrime = -1
while n % 2 == 0:
maxPrime = 2
n >>= 1
while n % 3 == 0:
maxPrime = 3
n=n/3
for i in range(5, int(math.sqrt(n)) + 1, 6):
while n % i == 0:
maxPrime = i
n = n / i
while n % (i+2) == 0:
maxPrime = i+2
n = n / (i+2)
if n > 4:
maxPrime = n
return int(maxPrime)
n = 15
print(maxPrimeFactors(n))
n = 25698751364526
print(maxPrimeFactors(n))
C#
using System;
class GFG {
static long maxPrimeFactors(long n)
{
long maxPrime = -1;
while (n % 2 == 0) {
maxPrime = 2;
n >>= 1;
}
while (n % 3 == 0) {
maxPrime = 3;
n = n / 3;
}
for (int i = 5; i <= Math.Sqrt(n); i += 6) {
while (n % i == 0) {
maxPrime = i;
n = n / i;
}
while (n % (i + 2) == 0) {
maxPrime = i + 2;
n = n / (i + 2);
}
}
if (n > 4)
maxPrime = n;
return maxPrime;
}
public static void Main()
{
long n = 15L;
Console.WriteLine(maxPrimeFactors(n));
n = 25698751364526L;
Console.WriteLine(maxPrimeFactors(n));
}
}
PHP
<?php
function maxPrimeFactors($n)
{
$maxPrime = -1;
while ($n % 2 == 0)
{
$maxPrime = 2;
$n >>= 1;
}
while ($n % 3 == 0) {
$maxPrime = 3;
$n=$n/3;
}
for ($i = 3; $i <= sqrt($n); $i += 2)
{
while ($n % $i == 0)
{
$maxPrime = $i;
$n = $n / $i;
}
while ($n % ($i+2) == 0) {
$maxPrime = $i+2;
$n = $n / ($i+2);
}
}
if ($n > 4)
$maxPrime = $n;
return $maxPrime;
}
$n = 15;
echo maxPrimeFactors($n), "n";
$n = 25698751364526;
echo maxPrimeFactors($n), "n";
?>
Javascript
<script>
function maxPrimeFactor(n) {
let maxPrime = -1;
while(n % 2 == 0) {
n = n / 2;
maxPrime = 2;
}
while(n % 3 == 0) {
n = n / 3;
maxPrime = 3;
}
for (let i = 5; i <= Math.sqrt(n); i += 6) {
while (n % i == 0) {
maxPrime = i;
n = n / i;
}
while (n % (i + 2) == 0) {
maxPrime = i + 2;
n = n / (i + 2);
}
}
return n > 4 ? n : maxPrime;
}
document.write(maxPrimeFactor(15));
document.write(maxPrimeFactor(25698751364526));
</script>
Time complexity: ![]()
Auxiliary space: ![]()
Method 2:
Follow the steps below for the implementation:
- Initialize variables largest_prime to -1, i to 2, and n to the input integer.
- Start a while loop that continues as long as i * i <= n. This loop will iterate through all possible factors of n.
- In the while loop, start another while loop that continues as long as n % i == 0. This inner loop will divide n by i until n is no longer divisible by i.
- In the inner loop, set largest_prime to i, and update n by dividing it by i.
- At the end of the inner loop, increment i by 1.
- After the outer loop, if n > 1, set largest_prime to n. This is because n could be a prime number larger than any of its factors.
- Return largest_prime.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int maxPrimeFactors(long long n)
{
int largest_prime = -1;
int i = 2;
while (i * i <= n) {
while (n % i == 0) {
largest_prime = i;
n = n / i;
}
i = i + 1;
}
if (n > 1) {
largest_prime = n;
}
return largest_prime;
}
int main()
{
long long n = 15;
cout << maxPrimeFactors(n) << endl;
n = 25698751364526;
cout << maxPrimeFactors(n) << endl;
return 0;
}
Python3
def gcd(a, b):
while(a > 0 and b > 0):
if (a > b):
a = a % b
else:
b = b % a
if (a == 0):
return b
return a
def pollard_rho(n):
if n == 1:
return []
if n % 2 == 0:
return [2] + pollard_rho(n // 2)
x = 2
y = 2
d = 1
while d == 1:
x = (x*x + 1) % n
y = (y*y + 1) % n
y = (y*y + 1) % n
d = gcd(abs(x-y), n)
if d == n:
return pollard_rho(n)
else:
return pollard_rho(d) + pollard_rho(n // d)
n = 15
print(pollard_rho(n))
Time complexity: O(sqrt(n)).
Auxiliary space: O(1)
Method 3: (Trial Division)
Trial Division is a simple algorithm for finding the prime factors of a given number. It works by dividing the number by all possible prime factors starting from 2, and adding each prime factor to a list of factors until the number becomes 1.
Follow the steps below for the implementation:
- Initialize an variable to hold the largest prime factor.
- Divide the given number by with all of its prime factors and compare them with factor variable and also decrement the number.
- If remaining number is greater than one, then compare it again with factor variable, otherwise skip it.
- Finally, return the factor which contains .
Below is the implementation of the above approach:
Python3
def max_prime_factor(n):
factor = 0
d = 2
while d*d <= n:
if (n % d) == 0:
factor = max(factor, d)
n //= d
d += 1
if n > 1:
factor = max(factor, n)
return factor
n = 15
print(max_prime_factor(n))
n = 25698751364526
print(max_prime_factor(n))
Time complexity: O(log(sqrt(n)) = O(log(n)), because in each iteration, n becomes n//d.
Auxiliary space: O(1), as it uses a constant amount of memory for storing the variables factor and d.
Last Updated :
09 May, 2023
Like Article
Save Article
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Теория чисел
- Простые числа
- Разложение на простые множители
- Решето Эратосфена
- Линейное решето Эратосфена*
- НОД и НОК
- Алгоритм Евклида
- Расширенный алгоритм Евклида*
- Операции по модулю
- Быстрое возведение в степень
- Деление по простому модулю*
Простые числа
Простым называется натуральное число, которое делится только на единицу и на себя. Единица при этом простым числом не считается. Составным числом называют непростое число, которое еще и не единица.
Примеры простых чисел: (2), (3), (5), (179), (10^9+7), (10^9+9).
Примеры составных чисел: (4), (15), (2^{30}).
Еще одно определение простого числа: (N) — простое, если у (N) ровно два делителя. Эти делители при этом равны (1) и (N).
Проверка на простоту за линию
С точки зрения программирования интересно научиться проверять, является ли число (N) простым. Это очень легко сделать за (O(N)) – нужно просто проверить, делится ли оно хотя бы на одно из чисел (2, 3, 4, ldots, N-1) . (N > 1) является простым только в случае, если оно не делится на на одно из этих чисел.
def is_prime(n):
if n == 1:
return False
for i in range(2, n): # начинаем с 2, так как на 1 все делится; n не включается
if n % i == 0:
return False
return True
for i in range(1, 10):
print(i, is_prime(i))(1, False)
(2, True)
(3, True)
(4, False)
(5, True)
(6, False)
(7, True)
(8, False)
(9, False)Проверка на простоту за корень
Алгоритм можно ускорить с (O(N)) до (O(sqrt{N})).
Пусть (N = a times b), причем (a leq b). Тогда заметим, что (a leq sqrt N leq b).
Почему? Потому что если (a leq b < sqrt{N}), то (ab leq b^2 < N), но (ab = N). А если (sqrt{N} < a leq b), то (N < a^2 leq ab), но (ab = N).
Иными словами, если число (N) равно произведению двух других, то одно из них не больше корня из (N), а другое не меньше корня из (N).
Из этого следует, что если число (N) не делится ни на одно из чисел (2, 3, 4, ldots, lfloorsqrt{N}rfloor), то оно не делится и ни на одно из чисел (lceilsqrt{N}rceil + 1, ldots, N-2, N-1), так как если есть делитель больше корня (не равный (N)), то есть делитель и меньше корня (не равный 1). Поэтому в цикле for достаточно проверять числа не до (N), а до корня.
def is_prime(n):
if n == 1:
return False
# Удобно вместо for i in range(2, n ** 0.5) писать так:
i = 2
while i * i <= n:
if n % i == 0:
return False
i += 1
return True
for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
print(i, is_prime(i))(1, False)
(2, True)
(3, True)
(10, False)
(11, True)
(12, False)
(1000000006, False)
(1000000007, True)Разложение на простые множители
Любое натуральное число можно разложить на произведение простых, и с такой записью очень легко работать при решении задач. Разложение на простые множители еще называют факторизацией.
[11 = 11 = 11^1] [100 = 2 times 2 times 5 times 5 = 2^2 times 5^2] [126 = 2 times 3 times 3 times 7 = 2^1 times 3^2 times 7^1]
Рассмотрим, например, такую задачу:
Условие: Нужно разбить (N) людей на группы равного размера. Нам интересно, какие размеры это могут быть.
Решение: По сути нас просят найти число делителей (N). Нужно посмотреть на разложение числа (N) на простые множители, в общем виде оно выглядит так:
[N= p_1^{a_1} times p_2^{a_2} times ldots times p_k^{a_k}]
Теперь подумаем над этим выражением с точки зрения комбинаторики. Чтобы «сгенерировать» какой-нибудь делитель, нужно подставить в степень (i)-го простого число от 0 до (a_i) (то есть (a_i+1) различное значение), и так для каждого. То есть делитель (N) выглядит ровно так: [M= p_1^{b_1} times p_2^{b_2} times ldots times p_k^{b_k}, 0 leq b_i leq a_i] Значит, ответом будет произведение ((a_1+1) times (a_2+1) times ldots times (a_k + 1)).
Алгоритм разложения на простые множители
Применяя алгоритм проверки числа на простоту, мы умеем легко находить минимальный простой делитель числа N. Ясно, что как только мы нашли простой делитель числа (N), мы можем число (N) на него поделить и продолжить искать новый минимальный простой делитель.
Будем перебирать простой делитель от (2) до корня из (N) (как и раньше), но в случае, если (N) делится на этот делитель, будем просто на него делить. Причем, возможно, нам понадобится делить несколько раз ((N) может делиться на большую степень этого простого делителя). Так мы будем набирать простые делители и остановимся в тот момент, когда (N) стало либо (1), либо простым (и мы остановились, так как дошли до корня из него). Во втором случае надо еще само (N) добавить в ответ.
Напишем алгоритм факторизации:
def factorize(n):
factors = []
i = 2
while i * i <= n: # перебираем простой делитель
while n % i == 0: # пока N на него делится
n //= i # делим N на этот делитель
factors.append(i)
i += 1
# возможно, в конце N стало большим простым числом,
# у которого мы дошли до корня и поняли, что оно простое
# его тоже нужно добавить в разложение
if n > 1:
factors.append(n)
return factors
for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
print(i, '=', ' x '.join(str(x) for x in factorize(i)))1 =
2 = 2
3 = 3
10 = 2 x 5
11 = 11
12 = 2 x 2 x 3
1000000006 = 2 x 500000003
1000000007 = 1000000007Задание
За сколько работает этот алгоритм?
.
.
.
.
Решение
За те же самые (O(sqrt{N})). Итераций цикла while с перебором делителя будет не больше, чем (sqrt{N}). Причем ровно (sqrt{N}) операций будет только в том случае, если (N) – простое.
А итераций деления (N) на делители будет столько, сколько всего простых чисел в факторизации числа (N). Понятно, что это не больше, чем (O(log{N})).
Задание
Докажите, что число (N) имеет не больше, чем (O(log{N})) простых множителей в факторизации.
Разные свойства простых чисел*
Вообще, про простые числа известно много свойств, но почти все из них очень трудно доказать. Вот еще некоторые из них:
- Простых чисел, меньших (N), примерно (frac{N}{ln N}).
- N-ое простое число равно примерно (Nln N).
- Простые числа распределены более-менее равномерно. Например, если вам нужно найти какое-то простое число в промежутке, то можно их просто перебрать и проверить — через несколько сотен какое-нибудь найдется.
- Для любого (N ge 2) на интервале ((N, 2N)) всегда найдется простое число (Постулат Бертрана)
- Впрочем, существуют сколь угодно длинные отрезки, на которых простых чисел нет. Самый простой способ такой построить – это начать с (N! + 2).
- Есть алгоритмы, проверяющие число на простоту намного быстрее, чем за корень.
- Максимальное число делителей равно примерно (O(sqrt[3]{n})). Это не математический результат, а чисто эмпирический — не пишите его в асимптотиках.
- Максимальное число делителей у числа на отрезке ([1, 10^5]) — 128
- Максимальное число делителей у числа на отрекзке ([1, 10^9]) — 1344
- Максимальное число делителей у числа на отрезке ([1, 10^{18}]) — 103680
- Наука умеет факторизовать числа за (O(sqrt[4]{n})), но об этом как-нибудь в другой раз.
- Любое число больше трёх можно представить в виде суммы двух простых (гипотеза Гольдбаха), но это не доказано.
Решето Эратосфена
Часто нужно не проверять на простоту одно число, а найти все простые числа до (N). В этом случае наивный алгоритм будет работать за (O(Nsqrt N)), так как нужно проверить на простоту каждое число от 1 до (N).
Но древний грек Эратосфен предложил делать так:
Запишем ряд чисел от 1 до (N) и будем вычеркивать числа: * делящиеся на 2, кроме самого числа 2 * затем деляющиеся на 3, кроме самого числа 3 * затем на 5, затем на 7, и так далее и все остальные простые до n. Таким образом, все незачеркнутые числа будут простыми — «решето» оставит только их.
Красивая визуализация
Задание
Найдите этим способом на бумажке все простые числа до 50, потом проверьте с программой:
N = 50
prime = [1] * (N + 1)
prime[0], prime[1] = 0, 0
for i in range(2, N + 1): # можно и до sqrt(N)
if prime[i]:
for j in range(2 * i, N + 1, i): # идем с шагом i, можно начиная с i * i
prime[j] = 0
for i in range(1, N + 1):
if prime[i]:
print(i)2
3
5
7
11
13
17
19
23
29
31
37
41
43
47У этого алгоритма можно сразу заметить несколько ускорений.
Во-первых, число (i) имеет смысл перебирать только до корня из (N), потому что при зачеркивании составных чисел, делящихся на простое (i > sqrt N), мы ничего не зачеркнем. Почему? Пусть существует составное (M leq N), которое делится на %i%, и мы его не зачеркнули. Но тогда (i > sqrt N geq sqrt M), а значит по ранее нами доказанному утверждению (M) должно делиться и на простое число, которое меньше корня. Но это значит, что мы его уже вычеркнули.
Во-вторых, по этой же самое причине (j) имеет смысл перебирать только начиная с (i^2). Зачем вычеркивать (2i), (3i), (4i), …, ((i-1)i), если они все уже вычеркнуты, так как мы уже вычеркивали всё, что делится на (2), (3), (4), …, ((i-1)).
Асимптотика
Такой код будет работать за (O(N log log N)) по причинам, которые мы пока не хотим объяснять формально.
Гармонический ряд
Научимся оценивать асимптотику величины (1 + frac{1}{2} + ldots + frac{1}{N}), которая нередко встречается в задачах, где фигурирует делимость.
Возьмем (N) равное (2^i – 1) и запишем нашу сумму следующим образом: [left(frac{1}{1}right) + left(frac{1}{2} + frac{1}{3}right) + left(frac{1}{4} + ldots + frac{1}{7}right) + ldots + left(frac{1}{2^{i – 1}} + ldots + frac{1}{2^i – 1}right)]
Каждое из этих слагаемых имеет вид [frac{1}{2^j} + ldots + frac{1}{2^{j + 1} – 1} le frac{1}{2^j} + ldots + frac{1}{2^j} = 2^j frac{1}{2^j} = 1]
Таким образом, наша сумма не превосходит (1 + 1 + ldots + 1 = i le 2log_2(2^i – 1)). Тем самым, взяв любое (N) и дополнив до степени двойки, мы получили асимптотику (O(log N)).
Оценку снизу можно получить аналогичным образом, оценив каждое такое слагаемое снизу значением (frac{1}{2}).
Попытка объяснения асимптотики** (для старших классов)
Мы знаем, что гармонический ряд (1 + frac{1}{2} + frac{1}{3} + ldots + frac{1}{N}) это примерно (log N), а значит [N + frac{N}{2} + frac{N}{3} + ldots + frac{N}{N} sim N log N]
А что такое асимптотика решета Эратосфена? Мы как раз ровно (frac{N}{p}) раз зачеркиваем числа делящиеся на простое число (p). Если бы все числа были простыми, то мы бы как раз получили (N log N) из формули выше. Но у нас будут не все слагаемые оттуда, только с простым (p), поэтому посмотрим чуть более точно.
Известно, что простых чисел до (N) примерно (frac{N}{log N}), а значит допустим, что k-ое простое число примерно равно (k ln k). Тогда
[sum_{substack{2 leq p leq N \ text{p is prime}}} frac{N}{p} sim frac{1}{2} + sum_{k = 2}^{frac{N}{ln N}} frac{N}{k ln k} sim int_{2}^{frac{N}{ln N}} frac{N}{k ln k} dk =N(lnlnfrac{N}{ln N} – lnln 2) sim N(lnln N – lnlnln N) sim N lnln N]
Но вообще-то решето можно сделать и линейным.
Задание
Решите 5 первых задач из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Линейное решето Эратосфена*
Наша цель — для каждого числа до (N) посчитать его минимальный простой делитель. Будем хранить его в массиве min_d. Параллельно будем хранить и список всех найденных простых чисел primes – это ровно те числа (x), у которых (min_d[x] = x).
Основное утверждение такое:
Пусть у числа (M) минимальный делитель равен (a). Тогда, если (M) составное, мы хотим вычеркнуть его ровно один раз при обработке числа (frac{M}{a}).
Мы также перебираем число (i) от (2) до (N). Если (min_d[i]) равно 0 (то есть мы не нашли ни один делитель у этого числа еще), значит оно простое – добавим в primes и сделаем (min_d[i] = i).
Далее мы хотим вычеркнуть все числа (i times k) такие, что (k) – это минимальный простой делитель этого числа. Из этого следует, что необходимо и достаточно перебрать (k) в массиве primes, и только до тех пор, пока (k < min_d[i]). Ну и перестать перебирать, если (i times k > N).
Алгоритм пометит все числа по одному разу, поэтому он корректен и работает за (O(N)).
N = 30
primes = []
min_d = [0] * (N + 1)
for i in range(2, N + 1):
if min_d[i] == 0:
min_d[i] = i
primes.append(i)
for p in primes:
if p > min_d[i] or i * p > N:
break
min_d[i * p] = p
print(i, min_d)
print(min_d)
print(primes)2 [0, 0, 2, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
3 [0, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
4 [0, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
5 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
6 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
7 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
8 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
9 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
10 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
11 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 5, 0, 3, 0, 0, 0]
12 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 0, 3, 0, 0, 0]
13 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 0, 0, 0]
14 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 0]
15 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
16 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
17 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
18 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
19 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
20 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
21 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
22 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
23 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
24 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
25 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
26 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
27 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
28 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
29 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
30 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]Этот алгоритм работает асимптотически быстрее, чем обычное решето. Но на практике, если писать обычное решето Эратсфена с оптимизациями, то оно оказывается быстрее линейнего. Также линейное решето занимает гораздо больше памяти – ведь в обычном решете можно хранить просто (N) бит, а здесь нам нужно (N) чисел и еще массив primes.
Зато один из «побочных эффектов» алгоритма — он неявно вычисляет факторизацию всех чисел от (1) до (N). Ведь зная минимальный простой делитель любого числа от (1) до (N) можно легко поделить на это число, посмотреть на новый минимальный простой делитель и так далее.
НОД и НОК
Введем два определения.
Наибольший общий делитель (НОД) чисел (a_1, a_2, ldots, a_n) — это максимальное такое число (x), что все (a_i) делятся на (x).
Наименьшее общее кратное (НОК) чисел (a_1, a_2, ldots, a_n) — это минимальное такое число (x), что (x) делится на все (a_i).
Например, * НОД(18, 30) = 6 * НОД(60, 180, 315) = 15 * НОД(1, N) = 1 * НОК(12, 30) = 6 * НОК(1, 2, 3, 4) = 12 * НОК(1, (N)) = (N)
Зачем они нужны? Например, они часто возникают в задачах.
Условие: Есть (N) шестеренок, каждая (i)-ая зацеплена с ((i-1))-ой. (i)-ая шестеренка имеет (a_i) зубчиков. Сколько раз нужно повернуть полносьтю первую шестеренку, чтобы все остальные шестеренки тоже вернулись на изначальное место?
Решение: Когда одна шестеренка крутится на 1 зубчик, все остальные тоже крутятся на один зубчик. Нужно найти минимальное такое число зубчиков (x), что при повороте на него все шестеренки вернутся в изначальное положение, то есть (x) делится на все (a_i), то есть это НОК((a_1, a_2, ldots, a_N)). Ответом будет (frac{x}{a_1}).
Еще пример задачи на применение НОД и НОК:
Условие: Город — это прямоугольник (n) на (m), разделенный на квадраты единичного размера. Вертолет летит из нижнего левого угла в верхний правый по прямой. Вертолет будит людей в квартале, когда он пролетает строго над его внутренностью (границы не считаются). Сколько кварталов разбудит вертолёт?
Решение: Вертолет пересечет по вертикали ((m-1)) границу. С этим ничего не поделать — каждое считается как новое посещение какого-то квартала. По горизонтали то же самое — ((n-1)) переход в новую ячейку будет сделан.
Однако еще есть случай, когда он пересекает одновременно обе границы (то есть пролетает над каким-нибудь углом) — ровно тот случай, когда нового посещения квартала не происходит. Сколько таких будет? Ровно столько, сколько есть целых решений уравнения (frac{n}{m} = frac{x}{y}). Мы как бы составили уравнение движения вертолёта и ищем, в скольки целых точках оно выполняется.
Пусть (t = НОД(n, m)), тогда (n = at, m = bt).
Тогда (frac{n}{m} = frac{a}{b} = frac{x}{y}). Любая дробь с натуральными числителем и знаменателем имеет ровно одно представление в виде несократимой дроби, так что (x) должно делиться на (a), а (y) должно делиться на (b). А значит, как ответ подходят ((a, b), (2a, 2b), (3a, 3b), cdots, ((t-1)a, (t-1)b)). Таких ответов ровно (t = НОД(n, m))
Значит, итоговый ответ: ((n-1) + (m-1) – (t-1)).
Кстати, когда (НОД(a, b) = 1), говорят, что (a) и (b) взаимно просты.
Алгоритм Евклида
Осталось придумать, как искать НОД и НОК. Понятно, что их можно искать перебором, но мы хотим хороший быстрый способ.
Давайте для начала научимся искать (НОД(a, b)).
Мы можем воспользоваться следующим равенством: [НОД(a, b) = НОД(a, b – a), b > a]
Оно доказывается очень просто: надо заметить, что множества общих делителей у пар ((a, b)) и ((a, b – a)) совпадают. Почему? Потому что если (a) и (b) делятся на (x), то и (b-a) делится на (x). И наоборот, если (a) и (b-a) делятся на (x), то и (b) делится на (x). Раз множства общих делитей совпадают, то и максимальный делитель совпадает.
Из этого равенства сразу следует следующее равенство: [НОД(a, b) = НОД(a, b operatorname{%} a), b > a]
(так как (НОД(a, b) = НОД(a, b – a) = НОД(a, b – 2a) = НОД(a, b – 3a) = ldots = НОД(a, b operatorname{%} a)))
Это равенство дает идею следующего рекурсивного алгоритма:
[НОД(a, b) = НОД(b operatorname{%} a, a) = НОД(a operatorname{%} , (b operatorname{%} a), b operatorname{%} a) = ldots]
Например: [НОД(93, 36) = ] [= НОД(36, 93spaceoperatorname{%}36) = НОД(36, 21) = ] [= НОД(21, 15) = ] [= НОД(15, 6) = ] [= НОД(6, 3) = ] [= НОД(3, 0) = 3]
Задание:
Примените алгоритм Евклида и найдите НОД чисел: * 1 и 500000 * 10, 20 * 18, 60 * 55, 34 * 100, 250
По-английски наибольший общий делитель — greatest common divisor. Поэтому вместо НОД будем в коде писать gcd.
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)
print(gcd(1, 500000))
print(gcd(10, 20))
print(gcd(18, 60))
print(gcd(55, 34))
print(gcd(100, 250))
print(gcd(2465473782, 12542367456))1
10
6
1
50
6Вообще, в C++ такая функция уже есть в компиляторе g++ — называется __gcd. Если у вас не Visual Studio, то, скорее всего, у вас g++. Вообще, там много всего интересного.
А за сколько оно вообще работает?
Задание
Докажите, что алгоритм Евклида для чисел (N), (M) работает за (O(log(N+M))).
Кстати, интересный факт: самыми плохими входными данными для алгоритма Евклида являются числа Фибоначчи. Именно там и достигается логарифм.
Как выразить НОК через НОД
(НОК(a, b) = frac{ab}{НОД(a, b)})
По этой формуле можно легко найти НОК двух чисел через их произведение и НОД. Почему она верна?
Посмотрим на разложения на простые множители чисел a, b, НОК(a, b), НОД(a, b).
[ a = p_1^{a_1}times p_2^{a_2}timesldotstimes p_n^{a_n} ] [ b = p_1^{b_1}times p_2^{b_2}timesldotstimes p_n^{b_n} ] [ ab = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} ]
Из определений НОД и НОК следует, что их факторизации выглядят так: [ НОД(a, b) = p_1^{min(a_1, b_1)}times p_2^{min(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)} ] [ НОК(a, b) = p_1^{max(a_1, b_1)}times p_2^{max(a_2, b_2)}timesldotstimes p_n^{max(a_n, b_n)} ]
Тогда посчитаем (НОД(a, b) times НОК(a, b)): [ НОД(a, b)НОК(a, b) = p_1^{min(a_1, b_1)+max(a_1, b_1)}times p_2^{min(a_2, b_2)+max(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)+max(a_n, b_n)} =] [ = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} = ab]
Формула доказана.
Как посчитать НОД/НОК от более чем 2 чисел
Для того, чтобы искать НОД или НОК у более чем двух чисел, достаточно считать их по цепочке:
(НОД(a, b, c, d, ldots) = НОД(НОД(a, b), c, d, ldots))
(НОК(a, b, c, d, ldots) = НОК(НОК(a, b), c, d, ldots))
Почему это верно?
Ну просто множество общих делителей (a) и (b) совпадает с множеством делителей (НОД(a, b)). Из этого следует, что и множество общих делителей (a), (b) и еще каких-то чисел совпадает с множеством общих делителей (НОД(a, b)) и этих же чисел. И раз совпадают множества общих делителей, то и наибольший из них совпадает.
С НОК то же самое, только фразу “множество общих делителей” надо заменить на “множество общих кратных”.
Задание
Решите задачи F, G, H, I из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Расширенный алгоритм Евклида*
Очень важным для математики свойством наибольшего общего делителя является следующий факт:
Для любых целых (a, b) найдутся такие целые (x, y), что (ax + by = d), где (d = gcd(a, b)).
Из этого следует, что существует решение в целых числах, например, у таких уравнений: * (8x + 6y = 2) * (4x – 5y = 1) * (116x + 44y = 4) * (3x + 11y = -1)
Мы сейчас не только докажем, что решения у таких уравнений существуют, но и приведем быстрый алгоритм нахождения этих решений. Здесь нам вновь пригодится алгоритм Евклида.
Рассмотрим один шаг алгоритма Евклида, преобразующий пару ((a, b)) в пару ((b, a operatorname{%} b)). Обозначим (r = a operatorname{%} b), то есть запишем деление с остатком в виде (a = bq + r).
Предположим, что у нас есть решение данного уравнения для чисел (b) и (r) (их наибольший общий делитель, как известно, тоже равен (d)): [bx_0 + ry_0 = d]
Теперь сделаем в этом выражении замену (r = a – bq):
[bx_0 + ry_0 = bx_0 + (a – bq)y_0 = ay_0 + b(x_0 – qy_0)]
Tаким образом, можно взять (x = y_0), а (y = (x_0 – qy_0) = (x_0 – (a operatorname{/} b)y_0)) (здесь (/) обозначает целочисленное деление).
В конце алгоритма Евклида мы всегда получаем пару ((d, 0)). Для нее решение требуемого уравнения легко подбирается — (d * 1 + 0 * 0 = d). Теперь, используя вышесказанное, мы можем идти обратно, при вычислении заменяя пару ((x, y)) (решение для чисел (b) и (a operatorname{%} b)) на пару ((y, x – (a / b)y)) (решение для чисел (a) и (b)).
Это удобно реализовывать рекурсивно:
def extended_gcd(a, b):
if b == 0:
return a, 1, 0
d, x, y = extended_gcd(b, a % b)
return d, y, x - (a // b) * y
a, b = 3, 5
res = extended_gcd(a, b)
print("{3} * {1} + {4} * {2} = {0}".format(res[0], res[1], res[2], a, b))3 * 2 + 5 * -1 = 1Но также полезно и посмотреть, как будет работать расширенный алгоритм Евклида и на каком-нибудь конкретном примере. Пусть мы, например, хотим найти целочисленное решение такого уравнения: [116x + 44y = 4] [(2times44+28)x + 44y = 4] [44(2x+y) + 28x = 4] [44x_0 + 28y_0 = 4] Следовательно, [x = y_0, y = x_0 – 2y_0] Будем повторять такой шаг несколько раз, получим такие уравнения: [116x + 44y = 4] [44x_0 + 28y_0 = 4, x = y_0, y = x_0 – 2y_0] [28x_1 + 16y_1 = 4, x_0 = y_1, y_0 = x_1 – y_1] [16x_2 + 12y_2 = 4, x_1 = y_2, y_1 = x_2 – y_2] [12x_3 + 4y_3 = 4, x_2 = y_3, y_2 = x_3 – y_3] [4x_4 + 0y_4 = 4, x_3 = y_4, y_3 = x_4 – 3 y_4] А теперь свернем обратно: [x_4 = 1, y_4 = 0] [x_3 = 0, y_3 =1] [x_2 = 1, y_2 =-1] [x_1 = -1, y_1 =2] [x_0 = 2, y_0 =-3] [x = -3, y =8]
Действительно, (116times(-3) + 44times8 = 4)
Задание
Решите задачу J из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34273
Операции по модулю
Выражение (a equiv b pmod m) означает, что остатки от деления (a) на (m) и (b) на (m) равны. Это выражение читается как «(a) сравнимо (b) по модулю (m)».
Еще это можно опрделить так: (a) сравнимо c (b) по модулю (m), если ((a – b)) делится на (m).
Все целые числа можно разделить на классы эквивалентности — два числа лежат в одном классе, если они сравнимы по модулю (m). Говорят, что мы работаем в «кольце остатков по модулю (m)», и в нем ровно (m) элементов: (0, 1, 2, cdots, m-1).
Сложение, вычитение и умножение по модулю определяются довольно интуитивно — нужно выполнить соответствующую операцию и взять остаток от деления.
С делением намного сложнее — поделить и взять по модулю не работает. Об этом подробнее поговорим чуть дальше.
a = 30
b = 50
mod = 71
print('{} + {} = {} (mod {})'.format(a, b, (a + b) % mod, mod))
print('{} - {} = {} (mod {})'.format(a, b, (a - b) % mod, mod)) # на C++ это может не работать, так как модуль от отрицательного числа берется странно
print('{} - {} = {} (mod {})'.format(a, b, (a - b + mod) % mod, mod)) # на C++ надо писать так, чтобы брать модулю от гарантированно неотрицательного числа
print('{} * {} = {} (mod {})'.format(a, b, (a * b) % mod, mod))
# print((a / b) % mod) # а как писать это, пока неясно30 + 50 = 9 (mod 71)
30 - 50 = 51 (mod 71)
30 - 50 = 51 (mod 71)
30 * 50 = 9 (mod 71)Задание
Посчитайте: * (2 + 3 pmod 5) * (2 * 3 pmod 5) * (2 ^ 3 pmod 5) * (2 – 4 pmod 5) * (5 + 5 pmod 6) * (2 * 3 pmod 6) * (3 * 3 pmod 6)
Для умножения (в C++) нужно ещё учитывать следующий факт: при переполнении типа всё ломается (разве что если вы используете в качестве модуля степень двойки).
intвмещает до (2^{31} – 1 approx 2 cdot 10^9).long longвмещает до (2^{63} – 1 approx 8 cdot 10^{18}).long long longв плюсах нет, при попытке заиспользовать выдает ошибкуlong long long is too long.- Под некоторыми компиляторами и архитектурами доступен
int128, но не везде и не все функции его поддерживают (например, его нельзя вывести обычными методами).
Зачем нужно считать ответ по модулю
Очень часто в задаче нужно научиться считать число, которое в худшем случае гораздо больше, чем (10^{18}). Тогда, чтобы не заставлять вас писать длинную арифметику, автор задачи часто просит найти ответ по модулю большого числа, обычно (10^9 + 7)
Кстати, вместо того, чтобы писать (1000000007) удобно просто написать (1e9 + 7). (1e9) означает (1 times 10^9)
int mod = 1e9 + 7; # В C++
cout << mod;1000000007N = 1e9 + 7 # В питоне такое число становится float
print(N)
print(int(N))1000000007.0
1000000007Быстрое возведение в степень
Задача: > Даны натуральные числа (a, b, c < 10^9). Найдите (a^b) (mod (c)).
Мы хотим научиться возводить число в большую степень быстро, не просто умножая (a) на себя (b) раз. Требование на модуль здесь дано только для того, чтобы иметь возможность проверить правильность алгоритма для чисел, которые не влезают в int и long long.
Сам алгоритм довольно простой и рекурсивный, постарайтесь его придумать, решая вот такие примеры (прямо решать необязательно, но можно придумать, как посчитать значение этих чисел очень быстро):
- (3^2)
- (3^4)
- (3^8)
- (3^{16})
- (3^{32})
- (3^{33})
- (3^{66})
- (3^{132})
- (3^{133})
- (3^{266})
- (3^{532})
- (3^{533})
- (3^{1066})
Да, здесь специально приведена такая последовательность, в которой каждое следующее число легко считается через предыдущее: его либо нужно умножить на (a=3), либо возвести в квадрат. Так и получается рекурсивный алгоритм:
- (a^0 = 1)
- (a^{2k}=(a^{k})^2)
- (a^{2k+1}=a^{2k}times a)
Нужно только после каждой операции делать mod: * (a^0 pmod c = 1) * (a^{2k} pmod c = (a^{k} pmod c)^2 pmod c) * (a^{2k+1} pmod c = ((a^{2k}pmod c) times a) pmod c)
Этот алгоритм называется быстрое возведение в степень. Он имеет много применений: * в криптографии очень часто надо возводить число в большую степень по модулю * используется для деления по простому модулю (см. далее) * можно быстро перемножать не только числа, но еще и матрицы (используется для динамики, например)
Асимптотика этого алгоритма, очевидно, (O(log c)) – за каждые две итерации число уменьшается хотя бы в 2 раза.
Задание
Решите задачу K из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Задание
Решите как можно больше задач из практического контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34273
Деление по модулю*
Давайте все-таки научимся не только умножать, но и делить по простому модулю. Вот только что это значит?
(a / b) = (a times b^{-1}), где (b^{-1}) – это обратный элемент к (b).
Определение: (b^{-1}) – это такое число, что (bb^{-1} = 1)
Утверждение: в кольце остатков по простому модулю (p) у каждого остатка (кроме 0) существует ровно один обратный элемент.
Например, обратный к (2) по модулю (5) это (3) ((2 times 3 = 1 pmod 5)))
Задание
Найдите обратный элемент к: * числу (3) по модулю (5) * числу (3) по модулю (7) * числу (1) по модулю (7) * числу (2) по модулю (3) * числу (9) по модулю (31)
Давайте докажем это утверждение: надо заметить, что если каждый ненулевой остаток (1, 2, ldots, (p-1)) умножить на ненулевой остаток (a), то получатся числа (a, 2a, ldots, (p-1)a) – и они все разные! Они разные, потому что если (xa = ya), то ((x-y)a = 0), а значит ((x – y) a) делится на (p), (a) – ненулевой остаток, а значит (x = y), и это не разные числа. И из того, что все числа получились разными, это все ненулевые, и их столько же, следует, что это ровно тот же набор чисел, просто в другом порядке!
Из этого следует, что среди этих чисел есть (1), причем ровно один раз. А значит существует ровно один обратный элемент (a^{-1}). Доказательство закончено.
Это здорово, но этот обратный элемент еще хочется быстро находить. Быстрее, чем за (O(p)).
Есть несколько способов это сделать.
Через малую теорему Ферма
Малая теорема Ферма: > (a^{p-1} = 1 pmod p), если (p) – простое, (a neq 0 pmod p)).
Доказательство: В предыдущем пункте мы выяснили, что множества чисел (1, 2, ldots, (p-1)) и (a, 2a, ldots, (p-1)a) совпадают. Из этого следует, что их произведения тоже совпадают по модулю: ((p-1)! = a^{p-1} (p-1)! pmod p).
((p-1)!neq 0 pmod p) а значит на него можно поделить (это мы кстати только в предыдущем пункте доказали, поделить на число – значит умножить на обратный к нему, который существует).
А значит, (a^{p – 1} = 1 pmod p).
Как это применить Осталось заметить, что из малой теоремы Ферма сразу следует, что (a^{p-2}) – это обратный элемент к (a), а значит мы свели задачу к возведению (a) в степень (p-2), что благодаря быстрому возведению в степень мы умеем делать за (O(log p)).
Обобщение У малой теоремы Ферма есть обобщение для составных (p):
Теорема Эйлера: > (a^{varphi(p)} = 1 pmod p), (a) – взаимно просто с (p), а (varphi(p)) – это функция Эйлера (количество чисел, меньших (p) и взаимно простых с (p)).
Доказывается теорема очень похоже, только вместо ненулевых остатков (1, 2, ldots, p-1) нужно брать остатки, взаимно простые с (p). Их как раз не (p-1), а (varphi(p)).
Для нахождения обратного по этой теореме достаточно посчитать функцию Эйлера (varphi(p)) и найти (a^{-1} = a^{varphi(p) – 1}).
Но с этим возникают большие проблемы: посчитать функцию Эйлера сложно. Более того, на предполагаемой невозможности быстро ее посчитать построены некоторые криптографические алгоритм типа RSA. Поэтому быстро делить по составному модулю этим способом не получится.
Через расширенный алгоритм Евклида
Этим способом легко получится делить по любому модулю! Рекомендую.
Пусть мы хотим найти (a^{-1} pmod p), (a) и (p) взаимно простые (а иначе обратного и не будет существовать).
Давайте найдем корни уравнения
[ax + py = 1]
Они есть и находятся расширенным алгоритмом Евклида за (O(log p)), так как (НОД(a, p) = 1), ведь они взаимно простые.
Тогда если взять остаток по модулю (p):
[ax = 1 pmod p]
А значит, найденный (x) и будет обратным элементом к (a).
То есть надо просто найти (x) из решения того уравнения по модулю (p). Можно брать по модулю прямо походу решения уравнения, чтобы случайно не переполниться.

Это изображение демонстрирует нахождение простых множителей числа 864. Сокращённый способ написания — 25 × 33
В теории чисел, простые множители (простые делители) положительного целого числа — это простые числа, которые делят это число нацело (без остатка)[1]. Выделить простые множители положительного целого числа означает перечислить эти простые множители вместе с их кратностями. Процесс определения простых множителей называется факторизацией целых чисел. Основная теорема арифметики утверждает, что любое натуральное число можно представить в виде единственного (с точностью до порядка следования) произведения простых множителей[2].
Чтобы сократить выражение, простые множители часто представляются в виде степеней простых чисел (кратностей). Например,
в котором множители 2, 3 и 5 имеют кратности 3, 2 и 1, соответственно.
Для простого множителя р числа n кратность числа p — это наибольший из показателей степени а, для которых ра делит n нацело.
Для положительного целого числа n, количество простых множителей n и сумма простых множителей n (без учёта кратности) — это примеры арифметических функций из n (аддитивных арифметических функций[fr][3]).
Полный квадрат[править | править код]
Квадрат числа имеет то свойство, что все его простые множители имеют чётные кратности. Например, число 144 (квадрат 12) имеет простые множители
В более понятной форме:
Поскольку каждый простой множитель присутствует здесь чётное число раз, исходное число можно представить в виде квадрата некоторого числа. Таким же образом, куб числа — это число, у которого кратности простых множителей делятся на три, и так далее.
Взаимно простые числа[править | править код]
Положительные целые числа, не имеющие общих простых множителей, называются взаимно простыми. Два целых числа a и b можно назвать взаимно простыми, если их наибольший общий делитель НОД(a, b) = 1. Если для двух целых чисел неизвестны их простые множители, то для определения того, являются ли они взаимно простыми, используется алгоритм Евклида; алгоритм выполняется за полиномиальное время по количеству цифр.
Целое число 1 является взаимно простым для любого положительного целого числа, включая само себя. Иными словами, число 1 не имеет простых множителей, оно — empty product. Это означает, что НОД(1, b) = 1 для любого b ≥ 1.
Криптографические приложения[править | править код]
Определение простых множителей числа — это пример задачи, которая часто используется для обеспечения криптографической защиты в системах шифрования[4]. Предполагается, что эта задача требует супер-полиномиального времени по количеству цифр. Это значит, что относительно легко сконструировать задачу, решение которой заняло бы больше времени, чем известный возраст Вселенной при текущем развитии компьютеров и с помощью современных алгоритмов.
Функции Омега[править | править код]
Функция ω(n) (омега) представляет собой число различных простых множителей n, в то время как функция Ω(n) (большая Омега) представляет собой число простых множителей n, пересчитанное с учётом кратности[2]. Если
тогда
Например, 24 = 23 × 31, Так что ω(24) = 2 и Ω(24) = 3 + 1 = 4.
- ω(n) для n = 1, 2, 3, … соответственно 0, 1, 1, 1, 1, 2, 1, 1, 1, … — последовательность A001221 в OEIS.
- Ω(n) для n = 1, 2, 3, … соответственно 0, 1, 1, 2, 1, 2, 1, 3, 2, … — последовательность A001222 в OEIS.
См. также[править | править код]
- Составное число
- Факторизация целых чисел — алгоритмическая проблема нахождения простых множителей заданного числа
- Делимость
- Таблица простых множителей
- Решето Эратосфена
- Теорема Эрдёша-Каца
- Криптографическая стойкость
Ссылки[править | править код]
- ↑ Jensen, Gary R. Arithmetic for Teachers: With Applications and Topics from Geometry (англ.). — American Mathematical Society, 2004.
- ↑ 1 2 Riesel, Hans (1994), Prime numbers and computer methods for factorization, Basel, Switzerland: Birkhäuser, ISBN 978-0-8176-3743-9
- ↑ Melvyn B. Nathanson. Additive Number Theory: the Classical Bases (англ.). — Springer-Verlag, 1996. — Vol. 234. — (Graduate Texts in Mathematics). — ISBN 0-387-94656-X.
- ↑ Menezes, Alfred; van Oorschot, Paul C.; Vanstone, Scott A. Handbook of Applied Cryptography (неопр.). — CRC Press, 1996. — ISBN 0-8493-8523-7.
Данная статья дает ответы на вопрос о разложении числа на простыне множители. Рассмотрим общее представление о разложении с примерами. Разберем каноническую форму разложения и его алгоритм. Будут рассмотрены все альтернативные способы при помощи использования признаков делимости и таблицы умножения.
Что значит разложить число на простые множители?
Разберем понятие простые множители. Известно, что каждый простой множитель – это простое число. В произведении вида 2·7·7·23 имеем, что у нас 4 простых множителя в виде 2,7,7,23.
Разложение на множители предполагает его представление в виде произведений простых. Если нужно произвести разложение числа 30, тогда получим 2,3,5. Запись примет вид 30=2·3·5. Не исключено, что множители могут повторяться. Такое число как 144 имеет 144=2·2·2·2·3·3.
Не все числа предрасположены к разложению. Числа, которые больше 1 и являются целыми можно разложить на множители. Простые числа при разложении делятся только на 1 и на самого себя, поэтому невозможно представить эти числа в виде произведения.
При z, относящемуся к целым числам, представляется в виде произведения а и b, где z делится на а и на b. Составные числа раскладывают на простые множители при помощи основной теоремы арифметики. Если число больше 1, то его разложение на множители p1, p2, …, pn принимает вид a=p1, p2, …, pn. Разложение предполагается в единственном варианте.
Каноническое разложение числа на простые множители
При разложении множители могут повторяться. Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель p1, который встречается s1 раз и так далее pn – sn раз. Таким образом разложение примет вид a=p1s1·a=p1s1·p2s2·…·pnsn. Эта запись имеет название канонического разложения числа на простые множители.
При разложении числа 609840 получим, что 609 840=2·2·2·2·3·3·5·7·11·11,его канонический вид будет 609 840=24·32·5·7·112. При помощи канонического разложения можно найти все делители числа и их количество.
Алгоритм разложения числа на простые множители
Чтобы правильно разложить на множители необходимо иметь представление о простых и составных числах. Смысл заключается в том, чтобы получить последовательное количество делителей вида p1, p2, …,pn чисел a, a1, a2, …, an-1, это дает возможность получить a=p1·a1, где a1=a:p1, a=p1·a1=p1·p2·a2, где a2=a1:p2, …, a=p1·p2·…·pn·an, где an=an-1:pn. При получении an=1, то равенство a=p1·p2·…·pn получим искомое разложение числа а на простые множители. Заметим, что p1≤p2≤p3≤…≤pn.
Для нахождения наименьших общих делителей необходимо использовать таблицу простых чисел. Это выполняется на примере нахождения наименьшего простого делителя числа z. При взятии простых чисел 2,3,5,11 и так далее, причем на них делим число z. Так как z не является простым числом, следует учитывать, что наименьшим простым делителем не будет больше z. Видно, что не существуют делителей z, тогда понятно, что z является простым числом.
Рассмотрим на примере числа 87. При его делении на 2 имеем, что 87:2=43 с остатком равным 1. Отсюда следует, что 2 делителем не может являться, деление должно производиться нацело. При делении на 3 получим, что 87:3=29. Отсюда вывод – 3 является наименьшим простым делителем числа 87.
При разложении на простые множители необходимо пользоваться таблицей простых чисел, где a. При разложении 95 следует использовать около 10 простых чисел, а при 846653 около 1000.
Рассмотрим алгоритм разложения на простые множители:
- нахождение наименьшего множителя при делителе p1 числа a по формуле a1=a:p1, когда a1=1, тогда а является простым числом и включено в разложение на множители, когда не равняется 1, тогда a=p1·a1 и следуем к пункту, находящемуся ниже;
- нахождение простого делителя p2 числа a1 при помощи последовательного перебора простых чисел, используя a2=a1:p2, когда a2=1, тогда разложение примет вид a=p1·p2, когда a2=1, тогда a=p1·p2·a2, причем производим переход к следующему шагу;
- перебор простых чисел и нахождение простого делителя p3 числа a2 по формуле a3=a2:p3, когда a3=1, тогда получим, что a=p1·p2·p3, когда не равняется 1, тогда a=p1·p2·p3·a3 и производим переход к следующему шагу;
- производится нахождение простого делителя pn числа an-1 при помощи перебора простых чисел с pn-1, а также an=an-1:pn, где an=1, шаг является завершающим, в итоге получаем, что a=p1·p2·…·pn.
Результат алгоритма записывается в виде таблицы с разложенными множителями с вертикальной чертой последовательно в столбик. Рассмотрим рисунок, приведенный ниже.
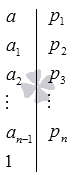
Полученный алгоритм можно применять при помощи разложения чисел на простые множители.
Примеры разложения на простые множители
Во время разложения на простые множители следует придерживаться основного алгоритма.
Произвести разложение числа 78 на простые множители.
Решение
Для того, чтобы найти наименьший простой делитель, необходимо перебрать все простые числа, имеющиеся в 78. То есть 78:2=39. Деление без остатка, значит это первый простой делитель, который обозначим как p1. Получаем, что a1=a:p1=78:2=39. Пришли к равенству вида a=p1·a1, где 78=2·39. Тогда a1=39, то есть следует перейти к следующему шагу.
Остановимся на нахождении простого делителя p2 числа a1=39. Следует перебрать простые числа, то есть 39:2=19 (ост. 1). Так как деление с остатком, что 2 не является делителем. При выборе числа 3 получаем, что 39:3=13. Значит, что p2=3 является наименьшим простым делителем 39 по a2=a1:p2=39:3=13. Получим равенство вида a=p1·p2·a2 в виде 78=2·3·13. Имеем, что a2=13 не равно 1, тогда следует переходит дальше.
Наименьший простой делитель числа a2=13 ищется при помощи перебора чисел, начиная с 3. Получим, что 13:3=4 (ост. 1). Отсюда видно, что 13 не делится на 5,7,11, потому как 13:5=2 (ост. 3), 13:7=1 (ост. 6) и 13:11=1 (ост. 2). Видно, что 13 является простым числом. По формуле выглядит так: a3=a2:p3=13:13=1. Получили, что a3=1, что означает завершение алгоритма. Теперь множители записываются в виде 78=2·3·13(a=p1·p2·p3).

Ответ: 78=2·3·13.
Разложить число 83 006 на простые множители.
Решение
Первый шаг предусматривает разложение на простые множители p1=2 и a1=a:p1=83 006:2=41 503, где 83 006=2·41 503.
Второй шаг предполагает, что 2, 3 и 5 не простые делители для числа a1=41 503, а 7 простой делитель, потому как 41 503:7=5 929. Получаем, что p2=7, a2=a1:p2=41 503:7=5 929. Очевидно, что 83 006=2·7·5 929.
Нахождение наименьшего простого делителя p4 к числу a3=847 равняется 7. Видно, что a4=a3:p4=847:7=121, поэтому 83 006=2·7·7·7·121.
Для нахождения простого делителя числа a4=121 используем число 11, то есть p5=11. Тогда получим выражение вида a5=a4:p5=121:11=11, и 83 006=2·7·7·7·11·11.
Для числа a5=11 число p6=11 является наименьшим простым делителем. Отсюда a6=a5:p6=11:11=1. Тогда a6=1. Это указывает на завершение алгоритма. Множители запишутся в виде 83 006=2·7·7·7·11·11.
Каноническая запись ответа примет вид 83 006=2·73·112.
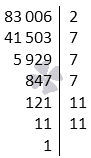
Ответ: 83 006=2·7·7·7·11·11=2·73·112.
Произвести разложение числа 897 924 289 на множители.
Решение
Для нахождения первого простого множителя произвести перебор простых чисел, начиная с 2. Конец перебора приходится на число 937. Тогда p1=937, a1=a:p1=897 924 289:937=958 297 и 897 924 289=937·958 297.
Второй шаг алгоритма заключается в переборе меньших простых чисел. То есть начинаем с числа 937. Число 967 можно считать простым, потому как оно является простым делителем числа a1=958 297. Отсюда получаем, что p2=967, то a2=a1:p1=958 297:967=991 и 897 924 289=937·967·991.
Третий шаг говорит о том, что 991 является простым числом, так как не имеет ни одного простого делителя, который не превосходит 991. Примерное значение подкоренного выражения имеет вид 991<402. Иначе запишем как 991<402. Отсюда видно, что p3=991 и a3=a2:p3=991:991=1. Получим, что разложение числа 897 924 289 на простые множители получается как 897 924 289=937·967·991.
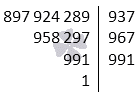
Ответ: 897 924 289=937·967·991.
Использование признаков делимости для разложения на простые множители
Чтобы разложить число на простые множители, нужно придерживаться алгоритма. Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.
Если необходимо произвести разложение на множители 10, то по таблице видно: 2·5=10. Получившиеся числа 2 и 5 являются простыми, поэтому они являются простыми множителями для числа 10.
Если необходимо произвести разложение числа 48, то по таблице видно: 48=6·8. Но 6 и 8 – это не простые множители, так как их можно еще разложить как 6=2·3 и 8=2·4. Тогда полное разложение отсюда получается как 48=6·8=2·3·2·4. Каноническая запись примет вид 48=24·3.
При разложении числа 3400 можно пользоваться признаками делимости. В данном случае актуальны признаки делимости на 10 и на 100. Отсюда получаем, что 3 400=34·100, где 100 можно разделить на 10, то есть записать в виде 100=10·10, а значит, что 3 400=34·10·10. Основываясь на признаке делимости получаем, что 3 400=34·10·10=2·17·2·5·2·5. Все множители простые. Каноническое разложение принимает вид 3 400=23·52·17.
Когда мы находим простые множители, необходимо использовать признаки делимости и таблицу умножения. Если представить число 75 в виде произведения множителей, то необходимо учитывать правило делимости на 5. Получим, что 75=5·15, причем 15=3·5. То есть искомое разложение пример вид произведения 75=5·3·5.
Загрузить PDF
Загрузить PDF
В этой статье мы расскажем вам, как разложить число на простые множители при помощи необычного метода — построения древовидной структуры множителей. Также здесь описаны способы вычисления наибольшего общего делителя и наименьшего общего кратного.
-

1
Запишите число на бумаге (сверху).
- Под числом нарисуйте две наклонные линии — одна направлена вправо, а вторая — влево.
- Или напишите число снизу и над ним нарисуйте две наклонные линии.
-
Пример: разложите на простые множители число 315.
- …..315
- …../…
-

2
Найдите любую пару множителей данного числа. Пара множителей — два числа, произведение которых равно исходному числу.[1]
- Эти два множителя надо записать под наклонными линиями.
- Вы можете выбрать любую пару множителей. Конечный результат не зависит от вашего выбора.
- Обратите внимание, что если у данного числа пар множителей нет (кроме 1 и самого числа), то это число простое и его нельзя разложить на множители.
-
Пример:
- …..315
- …../…
- …5….63
-

3
Для каждого из двух множителей напишите его пару множителей.
- Пара множителей — два числа, произведение которых равно исходному числу.
- Не пишите множители для простых чисел.
-
Пример:
- …..315
- …../…
- …5….63
- ………/
- …….7…9
-

4
Повторяйте процесс до тех пор, пока у вас не останутся только простые множители (простые числа). Простое число — это число, которое делится только на само себя и на 1.
- Продолжите рисовать наклонные линии и записывать пары множителей до тех пор, пока не столкнетесь с простыми числами.
- Обратите внимание, что в вашей древовидной структуре множителей числа 1 быть не должно.
-
Пример:
- …..315
- …../…
- …5….63
- ………/..
- …….7…9
- ………../..
- ……….3….3
-

5
Как только вы столкнулись с простым числом (простым множителем), выделите его (обведите или подчеркните), чтобы не потерять в разветвленной древовидной структуре множителей.
-
Пример: простыми множителями являются числа 5, 7, 3, 3
- …..315
- …../…
- …5….63
- …………/..
- ………7…9
- …………../..
- ………..3….3
- Альтернативный способ: переносите простые множители на каждый следующий уровень древовидной структуры множителей, и таким образом вы не потеряете их — все простые множители будут расположены на самом нижнем уровне.[2]
-
Пример:
- …..315
- …../…
- ….5….63
- …/……/..
- ..5….7…9
- ../…./…./..
- 5….7…3….3
-
Пример: простыми множителями являются числа 5, 7, 3, 3
-

6
Ответ записывается в виде произведения простых множителей.[3]
- Если преподаватель требует записать ответ в виде древовидной структуры множителей, то оставьте все как есть; в противном случае запишите ответ так:
- Пример: 5 * 7 * 3 * 3
-

7
Проверьте ответ. Перемножьте полученные простые множители, и вы должны получить исходное число.
- Пример: 5 * 7 * 3 * 3 = 315
Реклама
-

1
Для нахождения наибольшего общего делителя (НОД) двух или более чисел необходимо разложить эти числа на простые множители. Для этого воспользуйтесь вышеописанным методом.[4]
- Вам нужно будет создать древовидную структуру множителей для каждого числа.
- Для этого воспользуйтесь вышеописанным методом.
- НОД — это наибольшее число, которое нацело делит каждое данное число.
-
Пример: найдите НОД чисел 195 и 260.
- ……195
- ……/….
- ….5….39
- ………/….
- …….3…..13
- Простыми множителями числа 195 являются числа 3, 5, 13.
- …….260
- ……./…..
- ….10…..26
- …/… …/..
- .2….5…2…13
- Простыми множителями числа 260 являются числа: 2, 2, 5, 13.
-

2
После разложение чисел на простые множители запишите все простые множители отдельно для каждого числа. Затем выделите или выпишите все общие множители (множители, которые присутствуют в каждом списке простых множителей).
- Если в списках множителей нет общих, то НОД = 1.
- Пример: общими простыми множителями чисел 195 и 260 являются числа 5 и 13.
-

3
Перемножьте общие множители. Если у данных чисел несколько общих простых множителей, то необходимо перемножить их, чтобы найти НОД.[5]
- Если у данных чисел только один общий простой множитель, то он равен НОД.
-
Пример: общими множителями чисел 195 и 260 являются 5 и 13. Перемножьте их и получите:
- 5 * 13 = 65
-

4
Запишите ответ.
- Дважды проверьте ответ, разделив данные вам числа на найденный НОД. Если числа делятся на НОД нацело, то ответ правильный.
-
Пример: НОД чисел 195 и 260 равен 65.
- 195/65 = 3.
- 260/65 = 4.
Реклама
-

1
Для нахождения наименьшего общего кратного (НОК) двух или более чисел необходимо разложить эти числа на простые множители. Для этого воспользуйтесь вышеописанным методом.[6]
- Вам нужно будет создать древовидную структуру множителей для каждого числа.
- Для этого воспользуйтесь вышеописанным методом.
- НОК — это наименьшее число, которое нацело делится на каждое данное число.
-
Пример: найдите наименьшее общее кратное чисел 15 и 40.
- ….15
- …./..
- …3…5
- Простыми множителями числа 15 являются числа 3, 5.
- …..40
- …./…
- …5….8
- ……../..
- …….2…4
- …………/
- ……….2…2
- Простыми множителями числа 40 являются числа 5, 2, 2, 2.
-

2
После разложение чисел на простые множители запишите все простые множители отдельно для каждого числа. Затем выделите или выпишите все общие множители.
- Обратите внимание, что если вам даны три (или более) числа, общие множители должны присутствовать в списках множителей по крайней мере двух данных чисел (а не в каждом списке множителей).
- Не учитывайте двойные множители. Например, если в списке множителей первого числа множитель 2 присутствует два раза, а в списке множителей второго числа множитель 2 присутствует только один раз, вы должны отметить одну 2 в первом списке и одну 2 во втором (то есть вторую 2 в первом списке не учитывайте).
- Пример: общими множителями чисел 15 и 40 является только число 5.
-

3
Перемножьте общие множители и все множители, не являющиеся общими.[7]
- Здесь учитывайте все множители, не являющиеся общими. В приведенном выше примере вторая 2 из первого списка должна быть учтена. Общий же множитель трактуется как одно число.
-
Пример: общим множителем является число 5. Множителями, не являющимися общими, будут числа 3, 2, 2, 2. Таким образом, необходимо перемножить:
- 5 * 3 * 2 * 2 * 2 = 120.
-

4
Запишите ответ.
- Пример: НОК чисел 15 и 40 равен 120.
Реклама
Что вам понадобится
- Бумага
- Карандаш
Об этой статье
Эту страницу просматривали 9770 раз.





