Как найти наибольший радиус прямоугольника

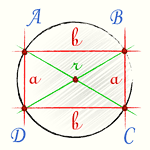
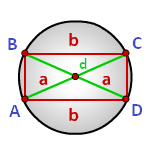
Радиус описанной окружности прямоугольника, формула

Формула радиуса описанной окружности прямоугольника выходит из теоремы Пифагора поскольку диагональ прямоугольника является диаметром описанной окружности.

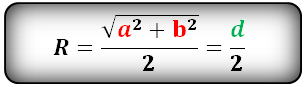
[R=frac{sqrt{a^2+b^2}}{2}]

(a,b – стороны прямоугольника; R – радиус описанной окружности прямоугольника)

Вычислить, найти радиус описанной окружности прямоугольника по формуле (1)

a (сторона прямоугольника)

b (сторона прямоугольника)

нажмите кнопку для расчета

Радиус описанной окружности прямоугольника	стр. 249

Свойства вписанного в круг прямоугольника

Геометрия периметр вписанного в круг прямоугольника.

Мы продолжаем находить свойства геометрических фигур с помощью перпендикулярных друг другу прямых. Мы уже нашли новое прочтение теоремы Пифагора,формулу площади треугольника
и площади круга.
Сегодня будем говорить о свойствах четырехугольника вписанного в круг.
Простейший вариант (Рис. 1) перпендикулярные прямые проходят через центр круга и прямоугольник это вписанный квадрат.
По теореме Пифагора нетрудно вычислить, что

СУММА СТОРОН КВАДРАТА РАВНА УДВОЕННОМУ КВАДРАТУ ДИАМЕТРА.
Далее ( Рис 2 ) . сумма квадратов сторон стремится к квадрату диаметра.

Прямоугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

• 1. Стороны прямоугольника являются его высотами.
• 2. Все углы прямоугольника прямые.
• 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
• 4. Диагонали прямоугольника равны.
• 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Диагональ прямоугольника

Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

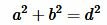(1)

Из равенства (1) найдем d:

.

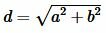(2)

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:

Ответ:

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

( small R=frac<large d> <large 2>)

(3)

Подставляя (3) в (2), получим:

( small R=frac<large sqrt> <large 2>)

(4)

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:

Ответ:

Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

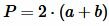(5)

где ( small a ) и ( small b ) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:

Ответ:

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

(6)

(7)

Из формулы (7) найдем ( small b ) и подставим в (6):

(8)

(9)

Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):

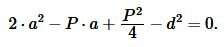(10)

Вычислим дискриминант квадратного уравнения (10):

Сторона прямоугольника вычисляется из следующих формул:

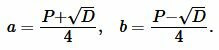(12)

После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

( frac< P><2>>d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*).

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

Решение геометрических задач на нахождение наибольшего и наименьшего значений с помощью производной

Планиметрические задачи

Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если:

Решение. Уравнение касательной будем искать по формуле ; уравнение нормали – по формуле По условию, .

Подставляем все найденные значения в уравнение касательной:

Теперь находим уравнение нормали:

Ответ: уравнение касательной:; уравнение нормали:

Задача 2.Написать уравнения касательной и нормали в точке

Подставим полученные решения в равенство

Найдем производную функции, заданной параметрически .

Подставляем все найденные значение в уравнение касательной:

Теперь находим уравнение нормали:

Ответ: уравнение касательной: уравнение нормали: .

Задача 3. Найти углы, под которыми пересекаются заданные кривые:

Решение. Угол между кривыми находится по формуле

Найдем координаты точки пересечения заданных кривых. Решаем систему уравнений:

Таким образом, кривые пересекаются в точках .

Далее найдем значения производных заданных функций в точках пересечения.

производный дифференцирование уравнение планиметрический

Подставляем найденные значение в формулу нахождения угла:

Ответ: в точке угол равен 0 (т.е. касательные совпадают), в точке угол равен .

Задача 4. Задан прямоугольник с периметром 56 см. Каковы должны быть его стороны, чтобы площадь была наибольшей [7]?

Обозначим одну из сторон за, тогда вторая сторона:

Площадь такого прямоугольника составит:

Требуется найти максимум функции .

Это квадратичная функция, ее график – парабола, ветви которой направлены вниз.

Определим критические точки: .

Так, – точка экстремума, слева от нее производная положительна, а справа – отрицательна.

Очевидно, что – точка максимума. В таком случае площадь прямоугольника максимальна, когда его стороны равны 14 см, то есть когда он является квадратом.

Ответ: площадь максимальна, когда стороны прямоугольника равны 14 см.

Задача 5. Площадь прямоугольника составляет . Каковы должны быть его размеры этого прямоугольника, чтобы периметр был минимальным?[7]

Пусть стороны прямоугольника равны . Тогда:

Периметр такого прямоугольника составит:

Требуется найти минимум данной функции. Найдём производную:

Найдем точки экстремума:

Очевидно, что , поэтому нас интересует точка .Слева от нее производная отрицательна, а справа – положительна.

Так, – точка минимума.

Ответ: чтобы периметр прямоугольника был минимальным, его стороны должны составить 4 см.

Задача 6. Две стороны параллелограмма лежат на сторонах заданного треугольника, а одна из его вершин принадлежит третьей стороне. Найти условия, при которых площадь параллелограмма является наибольшей [2].

Пусть треугольник определяется двумя сторонами и углом между ними (рис.4). Построим параллелограмм в соответствии с условиями задачи. Обозначим стороны параллелограмма Площадь параллелограмма определяется формулой

Выразим через и стороны треугольника . Из подобия треугольников и следует, что

В результате площадь записывается как функция:

Отсюда видно, что экстремум функциисуществует в следующей точке:

При переходе через эту точку производная меняет свой знак с плюса на минус, то есть эта точка является точкой максимума. Другая сторона параллелограмма при этом равна

Итак, вписанный в треугольник параллелограмм со сторонами имеет наибольшую площадь при условии

где стороны треугольника. Интересно, что результат не зависит от угла между сторонами треугольника.

Ответ: площадь параллелограмма является наибольшей при условии

где стороны треугольника.

Задача 7.Среди всех равнобедренных треугольников, вписанных в данную окружность, найти треугольник с наибольшим периметром [2].

Пусть треугольник вписан в окружность данного радиуса ,

(независимая переменная) (рис.5). Выразим периметр треугольника как функцию . По теореме синусов:

. Найдем, при каком значении функция принимает наибольшее значение на данном интервале

следовательно, точка максимума, в которой функция принимает наибольшее значение на заданном промежутке. Таким образом, наибольший периметр имеет равносторонний треугольник.

Ответ: среди всех равнобедренных треугольник, вписанных в данную окружность, с наибольшим периметром является равносторонний треугольник.

Задача 8.Окно имеет форму прямоугольника, ограниченного сверху полукругом.

Периметр окна равен . Определить радиус полукруга , при котором площадь окна является наибольшей (рис.6) [2].

Очевидно, что одна сторона прямоугольника равна . Другую сторону обозначим через . Периметр всего окна выражается формулой

Площадь окна составляет:

Полученное выражение представляет собой функцию . Исследуем ее на экстремум. Находим производную:

Определяем стационарные точки:

Поскольку вторая производная отрицательна:

то найденная точка является точкой максимума, т.е. при этом значении площадь окна будет наибольшей.

Само максимальное значение площади составляет

Ответ: радиус полукруга , при котором площадь является наибольшей.

[spoiler title=”источники:”]

http://matworld.ru/geometry/pryamougolnik.php

http://vuzlit.ru/2303757/reshenie_geometricheskih_zadach_nahozhdenie_naibolshego_naimenshego_znacheniy_pomoschyu_proizvodnoy

[/spoiler]

Прямоугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

Кроме этого:

• 1. Стороны прямоугольника являются его высотами.
• 2. Все углы прямоугольника прямые.
• 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
• 4. Диагонали прямоугольника равны.
• 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Диагональ прямоугольника

Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

или

Из равенства (1) найдем d:

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:

Ответ:

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

Подставляя (3) в (2), получим:

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:

Ответ:

Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

где ( small a ) и ( small b ) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:

Ответ:

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

Из формулы (7) найдем ( small b ) и подставим в (6):

Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):

Вычислим дискриминант квадратного уравнения (10):

Сторона прямоугольника вычисляется из следующих формул:

После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

Радиус описанной окружности прямоугольника