Лично я думаю, что нам с вами ещё повезло. Зачастую авторы вопросов по геометрии на БВ и вовсе не удосуживаются показать нам хоть какую-нибудь картинку. А здесь имеется некоторое изображение, с которым предстоит познакомиться поближе. Внешняя оценка подсказывает, что трапеция действительно является прямоугольной, а её прямые углы расположены с левой стороны. Но будет гораздо удобнее, если мы обозначим все вершины буквами из латиницы, как это делали в школе, а уже потом приступим к поиску ответа на вопрос:
Если прямые углы слева, тогда справа мы получим два разных угла – один острый, а второй непременно будет тупым. Почему так? Ну, если углы и справа будут прямыми (=90°), тогда мы получим прямоугольник и вовсе квадрат. А в задании всё-таки говорится о трапеции. И тогда остаётся прикинуть – угол ∠C явно тупой, а острым будет ∠D. Заданное значение 58° явно меньше, чем 90°. Следовательно, оно относится к острому углу ∠D, а искать мы будем значение ∠C.
Теперь самое главное – как? Можно провести перпендикуляр, отделив прямоугольник (или квадрат), а для оставшегося треугольника вспомнить свойство – сумма его углов, как известно из школьного курса, равна 180°. Это один вариант. Можно воспользоваться вторым. При этом речь идёт о четырёхугольнике, а в нём сумма внутренних углов равна 360° (=180°*(n-2), где n – число сторон). Из этого числа вычитаем два прямых угла по 90°, а потом и заданное значение 58°. Так мы тоже получим правильный ответ.
Но так получилось, что мне сегодня уже довелось один раз решать подобную задачу. И там уже говорил, что трапеции обладают довольно большим количество различных свойств. Например, у равнобедренных трапеций углы у оснований равны между собой. Прямоугольным трапециям это не характерно, но соблюдается другое общее для всех трапеций свойство – суммы углов при боковых сторонах равны =180°. Таким образом, если вам известен один, не составит большого труда отыскать второй:
- ∠A + ∠B = 180°
- 90° + 90° = 180° – всё верно
- ∠C + ∠D = 180°
- ∠C + 58° = 180°
- ∠C = 180° – 58° = 122°
То есть всё можно было сделать очень просто – если один угол =58°, вычтите это значение из 180° и вы получите правильный ответ.
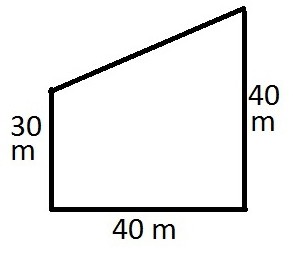
Один из углов прямоугольной трапеции равен 64°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Начнём с того, что у прямоугольной трапеции два угла имеют величину в 90°. По этой причине найти неизвестный угол будет легко и просто. Из большего угла рисуем отрезок перпендикулярный основанию трапеции и получаем вот такую картинку.
Угол D по условию задачи равен 64°. На рисунке имеет место быть прямоугольный треугольник в котором два угла известны, зная, что сумма всех углов в треугольнике равна 180° легко вычислить неизвестный нам угол.
180°-90°-64°=26°
Дело за малым — вычисляем угол С. Он складывается из двух углов одного из треугольника, другого из прямоугольника. В последнем он равен 90°. Соответственно результатом сложения будет величина в 116°.
Боковые стороны прямоугольной трапеции относятся как 1 : 2.
Найдите наибольший угол трапеции.
Вы открыли страницу вопроса Боковые стороны прямоугольной трапеции относятся как 1 : 2?. Он относится к категории
Геометрия. Уровень сложности вопроса – для учащихся 5 – 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Геометрия,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.
Задачи с трапецией не кажутся сложными в ряде фигур, которые изучены ранее. Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
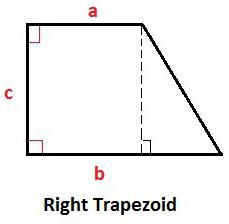
Определение прямоугольной трапеции и ее свойства
У произвольной трапеции основания параллельны, а боковые стороны могут иметь произвольное значение углов к ним. Если рассматривается прямоугольная трапеция, то в ней одна из сторон всегда перпендикулярна основаниям. То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
Другие углы в прямоугольной трапеции − это всегда острый и тупой. Причем их сумма всегда будет равна 180 градусам.
Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Какие обозначения приняты в представленных формулах?
Все величины, используемые в разных выражениях, которые описывают трапецию, удобно сразу оговорить и представить в таблице:
| Величина | Ее обозначение |
| a | большее основание |
| b | меньшее основание прямоугольной трапеции |
| c, h | перпендикулярная к основаниям боковая сторона, высота |
| d | наклонная боковая сторона |
| α | острый угол |
| β | тупой угол |
| м | средняя линия трапеции |
| д1 | меньшая диагональ |
| д2 | большая диагональ |
Формулы, которые описывают элементы прямоугольной трапеции
Самая простая из них связывает высоту и меньшую боковую сторону:
c = h.
Еще несколько формул для этой стороны прямоугольной трапеции:
с = d *sinα;
c = (a – b) * tg α;
c = √ (d2 – (a – b)2).
Первая вытекает из прямоугольного треугольника. И говорит о том, что катет к гипотенузе дает синус противолежащего угла.
В том же треугольнике второй катет равен разности двух оснований. Поэтому справедливо утверждение, которое приравнивает тангенс угла к отношению катетов.
Из того же треугольника можно вывести формулу, основываясь на знании теоремы Пифагора. Это третье записанное выражение.
Можно записать формулы для другой боковой стороны. Их тоже три:
d = (a – b) /cosα;
d = c / sin α;
d = √ (c2 + (а – b)2).
Первые две опять получаются из соотношения сторон в том же прямоугольном треугольнике, а вторая выводится из теоремы Пифагора.
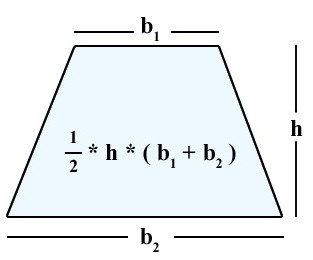
Какой формулой можно воспользоваться для расчета площади?
Той, что дана для произвольной трапеции. Только нужно учесть, что высотой является сторона, перпендикулярная к основаниям.
S = (a + b) * h / 2.
Эти величины не всегда даны явно. Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
Как быть, если нужно вычислить диагонали?
В этом случае нужно увидеть, что они образуют два прямоугольных треугольника. Значит, всегда можно воспользоваться теоремой Пифагора. Тогда первая диагональ будет выражаться так:
d1 = √ (с2 + b2)
или по-другому, заменив «с» на «h»:
d1 = √ (h2 + b2).
Аналогичным образом получаются формулы для второй диагонали:
d2 = √ (с2 + b2) или d2 = √ (h2 + а2).
Задача №1
Условие. Площадь прямоугольной трапеции известна и равна 120 дм2. Ее высота имеет длину 8 дм. Необходимо вычислить все стороны трапеции. Дополнительным условием является то, что одно основание меньше другого на 6 дм.
Решение. Поскольку дана прямоугольная трапеция, в которой известна высота, то сразу же можно сказать о том, что одна из сторон равна 8 дм, то есть меньшая боковая сторона.
Теперь можно сосчитать другую: d = √ (с2 + (а – b)2). Причем здесь сразу даны и сторона с, и разность оснований. Последнее равно 6 дм, это известно из условия. Тогда d будет равняться квадратному корню из (64 + 36), то есть из 100. Так найдена еще одна боковая сторона, равная 10 дм.
Сумму оснований можно найти из формулы для площади. Она будет равна удвоенному значению площади, разделенному на высоту. Если считать, то получается 240 / 8. Значит, сумма оснований — это 30 дм. С другой стороны, их разность равна 6 дм. Объединив эти уравнения, можно сосчитать оба основания:
а + b = 30 и а – b = 6.
Можно выразить а как (b + 6), подставить его в первое равенство. Тогда получится, что 2b будет равняться 24. Поэтому просто b окажется 12 дм.
Тогда последняя сторона а равна 18 дм.
Ответ. Стороны прямоугольной трапеции: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Задача №2
Условие. Дана прямоугольная трапеция. Ее большая боковая сторона равняется сумме оснований. Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Решение. Начать нужно с искомого. Нужная площадь определится как произведение a и b. Обе эти величины не известны.
Потребуется использовать дополнительные равенства. Одно из них построено на утверждении из условия: d = а + b. Необходимо воспользоваться третьей формулой для этой стороны, которая дана выше. Получится: d2 = с2 + (a – b)2 или (a + b)2 = с2 + (a – b)2.
Необходимо сделать преобразования, подставив вместо с его значение из условия – 12. После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
В начале решения шла речь о том, что а*b дает искомую площадь. Поэтому в последнем выражении можно заменить это произведение на S. Простой расчет даст значение площади. S = 36 см2.
Ответ. Искомая площадь 36 см2.
Задача №3
Условие. Площадь прямоугольной трапеции 150√3 см². Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Решение. Из свойства углов трапеции получается, что ее тупой угол равен 120º. Тогда диагональ делит его на равные, потому что одна его часть уже 60 градусов. Тогда и угол между этой диагональю и вторым основанием тоже 60 градусов. То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
Теперь нужно рассмотреть прямоугольный треугольник. В нем третий угол равен 30 градусам. Значит катет, лежащий против него, равен половине гипотенузы. То есть меньшее основание трапеции равно половине искомой диагонали: b = a/2. Из него же нужно найти высоту, равную боковой стороне, перпендикулярной основаниям. Сторона с здесь катет. Из теоремы Пифагора:
с = (a/2) * √3.
Теперь осталось только подставить все величины в формулу площади:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Решение этого уравнения дает корень 20
Ответ. Меньшая диагональ имеет длину 20 см.