Как найти наибольший угол ромба - Сайт, где вы сможете решить свои вопросы

Как найти больший угол ромба

Ромбом называют четырехугольник, у которого все стороны одинаковы, а углы не равны. Эта геометрическая фигура обладает уникальными свойствами, которые значительно облегчают расчеты. Чтобы найти ее больший угол, нужно знать еще несколько параметров.

Вам понадобится

– таблица синусов;
– таблица косинусов;
– таблица тангенсов.

Инструкция

В условиях задачи может быть указан меньший угол. Вспомните, чему равна сумма углов, прилежащих к одной стороне. Она у любого ромба составляет 180°. То есть вам достаточно из 180° вычесть размер известного угла. Начертите ромб. Обозначьте больший угол как α, а меньший – как β. Формула в этом случае будет выглядеть как α=180°-β.

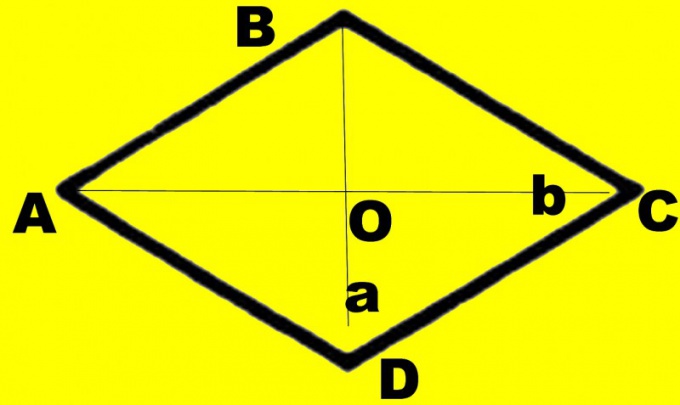
В задаче могут быть указаны также размер стороны и длина одной из диагоналей. В этом случае нужно вспомнить свойства диагоналей ромба. В точке пересечения они делятся пополам. Диагонали перпендикулярны друг другу, то есть при решении задачи можно будет использовать свойства прямоугольных треугольников. Еще одна важная деталь каждая из диагоналей одновременно является и биссектрисой угла.

Для наглядности сделайте чертеж. Начертите ромб ABCD. Проведите в нем диагонали d1 и d2. Допустим, известная вам диагональ d1 соединяет меньшие углы. Обозначьте точку их пересечения как О, большие углы ABC и CDA– как α, а меньшие – как β. Каждый из углов делится диагональю пополам. Рассмотрите прямоугольный треугольник АОВ. Вам известны стороны АВ и ОА, равная половине диагонали d1. Они представляют собой гипотенузу и катет противолежащего угла.

Вычислите синус угла АВО. Он равен отношению катета ОА к гипотенузе АВ, то есть sinАВО= ОА/АВ. По таблице синусов найдите размер угла. Вспомните, что он равен половине большего угла ромба. Соответственно, для определения искомого полученный размер умножьте на 2.

Если в условиях дан размер диагонали d2, соединяющей большие углы, способ решения будет аналогичен предыдущему, только вместо синуса используется косинус – отношение прилежащего катета к гипотенузе.

В условиях могут быть заданы только размеры диагоналей. В этом случае тоже понадобится чертеж, но, в отличие от предыдущих задач, он может быть точным. Проведите диагональ d1. Разделите ее пополам. К точке пересечения проведите диагональ d2 так, чтобы она тоже делилась на две равные части. Концы отрезков соедините по периметру. Обозначьте ромб как ABCD, точку пересечения диагоналей – как О.

Сторону ромба в данном случае вам вычислять не нужно. У вас образовался прямоугольный треугольник АОВ, у которого вам известны два катета. Отношение противолежащего катета к прилежащему называется тангенсом. Чтобы найти tgАВО, разделите ОА на ОВ. Найдите в таблице тангенсов нужное значение угла, а затем умножьте его на два.

Некоторые компьютерные программы позволяют не только вычислить больший угол ромба по заданным параметрам, но и сразу же начертить эту геометрическую фигуру. Это можно сделать, например, в программе AutoCAD. В этом случае таблицы синусов и тангенсов, конечно же, не нужны.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Геометрия,

вопрос задал 0nikitashindin0,

8 месяцев назад

Ответы на вопрос

Ответил KuOV

Ответ:

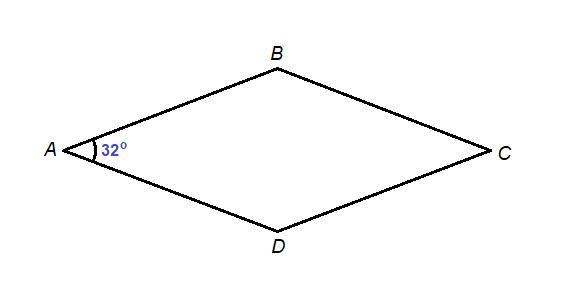
Больший угол равен 148°.

Объяснение:

Сумма углов ромба, прилежащих к одной стороне, равна 180°.

∠А = 32°

∠А + ∠В = 180°

∠В = 180° – ∠А = 180° – 32° = 148°

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика,
1 месяц назад

Грибы при сушке теряют 75% массы . Сколько понадобиться свежих грибов для приготовления 4 кг сушеных?

Математика,
1 месяц назад

Миша любит путешествовать. Однажды он проехал 3 часа на автобусе со скоростью 54км/ч;оказалось,что это шестая часть его пути. Остальную часть он ехал поездом. Сколько километров Миша проехал на…

Математика,
8 месяцев назад

НСК чисел 8 и 10 Срочно…

Другие предметы,
8 месяцев назад

Помогите с черчением.
По двум заданным видам построить третий вид. Построить наклонное сечение. (секущая плоскость АА)…

Физика,
6 лет назад

изобразите магнитное поле различных источников указав его направления Помогите пожалуйста…

Биология,
6 лет назад

определить структуру составляющие пкреферическую нервную систему .

Источник

Геометрия

Предыдущий вопрос

Следующий вопрос

Сторона ромба ровна его диагонали. Найдите больший угол ромба. Ответ дайте в градусах.

простак2
8 лет назад

Ответ

Ответ дан

igir12370

Диагональ делит ромб на 2 равносторонних треугольника.
Значит, меньший угол ромба 60 градусов ( в равностороннем треугольнике 3 угла по 60 град.)
Больший угол ромба равен 360-(60+60)=240 240:2=120
ответ 120

Ответы и объяснения

простак2

Не тот ответ, который тебе нужен?

Найди нужный

Источник

Найти углы ромба, зная только его сторону, нельзя: существуют ромбы, имеющие разные углы, но одинаковые стороны. На пальцах: сделайте ромб из проволоки, “сплющите” его — он останется ромбом, стороны будут те же, углы изменятся.

Значит, чтобы найти углы ромба нужно знать что-то ещё (или что-то другое). Например, зная сторону и диагональ, найти угол можно по теореме косинусов: если x — сторона, d — диагональ, a — угол напротив диагонали, то условие теоремы косинуов — d^2 = x^2 + x^2 – 2 * x^2 * cos(a), из него следует a = arccos((2x^2 – d^2)/2x^2). (Я говорю “найти угол”, а не “найти углы”, потому что если мы знаем один угол, остальные находятся тривиально: если один угол равен а градусов, то угол напротив него тоже а, остальные два — по 180-а).

Есть и другие варианты: через сторону и площадь (пользуясь тем, что площадь — это квадрат стороны умножить на синус угла), через две диагонали (мы знаем, что диагонали в ромбе пересекаются под прямым углом и делятся точкой пересечения пополам — отсюда следует, что тангенс половины угла ромба равен отношению диагоналей, просто по определнию тангенса; зная сторону и диагональ, кстати, тоже можно искать угол примерно таким способом, вместо теоремы косинусов) и так далее.

Источник

Если известны угол, лежащий напротив диагонали ромба, и эта диагональ, то, используя свойства ромба, можно найти остальные его элементы.

1) Большая диагональ ромба равна D. Напротив неё лежит угол β.

Большая диагональ AC=D, лежащий напротив неё угол ∠ABC=β (угол ромба, лежащий против большей диагонали — тупой).

Проведём вторую диагональ ромба BD, BD ∩ AC=O.

По свойствам ромба, его диагонали взаимно перпендикулярны, являются биссектрисами углов ромба и в точке пересечения делятся пополам. Следовательно, в прямоугольном треугольнике ABO

∠ABO=β/2, AO=D/2. По определению синуса,

$[sin angle ABO = frac{{AO}}{{AB}}, Rightarrow AB = frac{{AO}}{{sin angle ABO}},]$

$[AB = frac{{frac{D}{2}}}{{sin frac{beta }{2}}} = frac{D}{{2sin frac{beta }{2}}}.]$

Зная сторону ромба, можем найти его периметр:

$[{P_{ABCD}} = 4AB,{P_{ABCD}} = frac{{4D}}{{2sin frac{beta }{2}}} = frac{{2D}}{{sin frac{beta }{2}}}.]$

По определению котангенса,

$[ctgangle ABO = frac{{BO}}{{AO}}, Rightarrow BO = AO cdot ctgangle ABO,]$

$[BO = frac{D}{2}ctgfrac{beta }{2}, Rightarrow BD = 2 cdot frac{D}{2}ctgfrac{beta }{2} = D cdot ctgfrac{beta }{2}.]$

Площадь ромба может быть найдена как половина произведения его диагоналей:

$[{S_{ABCD}} = frac{1}{2} cdot AC cdot BD, Rightarrow ]$

$[{S_{ABCD}} = frac{1}{2} cdot D cdot D cdot ctgfrac{beta }{2} = frac{1}{2} cdot {D^2}ctgfrac{beta }{2}.]$

Другой вариант — произведение квадрата стороны на синус угла:

$[{S_{ABCD}} = A{B^2} cdot sin angle ABC,]$

$[{S_{ABCD}} = {(frac{D}{{2sin frac{beta }{2}}})^2} cdot sin beta .]$

(Упростив эту формулу, получим предыдущую).

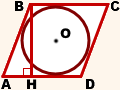Высоту ромба можно найти несколькими способами. Например, через площадь. С одной стороны, площадь ромба

$[{S_{ABCD}} = A{B^2} cdot sin angle ABC,]$

с другой —

$[{S_{ABCD}} = AD cdot BH.]$

Приравняв правые части формул:

$[AD cdot BH = A{B^2} cdot sin angle ABC]$

и разделив обе части равенства на AB (AD=AB), получим

(Можно найти BH непосредственно из прямоугольного треугольника ABH по определению синуса, ∠BAH=180º-β, sin∠BAH=sin(180º-β)=sinβ).

$[BH = frac{{D cdot sin beta }}{{2sin frac{beta }{2}}} = frac{{D cdot 2sin frac{beta }{2}cos frac{beta }{2}}}{{2sin frac{beta }{2}}} = Dcos frac{beta }{2}.]$

Радиус вписанной окружности равен половине высоты ромба

$[r = frac{1}{2}h,r = frac{1}{2} cdot Dcos frac{beta }{2} = frac{D}{2}cos frac{beta }{2}.]$

2) Меньшая диагональ ромба равна d. Напротив неё лежит угол α.

Аналогично, из прямоугольного треугольника ABO

$[AB = frac{d}{{2sin frac{alpha }{2}}},]$

$[AO = frac{d}{2}ctgfrac{alpha }{2},AC = d cdot ctgfrac{alpha }{2},]$

$[{P_{ABCD}} = frac{{2d}}{{sin frac{alpha }{2}}},]$

$[{S_{ABCD}} = frac{1}{2} cdot {d^2}ctgfrac{alpha }{2},]$

$[BH = frac{{dsin alpha }}{{2sin frac{alpha }{2}}} = frac{{d cdot 2sin frac{alpha }{2}cos frac{alpha }{2}}}{{2sin frac{alpha }{2}}} = dcos frac{alpha }{2},]$