Как найти наибольшую биссектриса равнобедренного треугольника

Вычисление биссектрисы треугольника с известными свойствами

Математика, как известно, царица наук. Неслучайно это выражение так любят учителя, особенно старой формации. Математика открывается исключительно тем, кто умеет, во-первых, логически мыслить, а во-вторых, тем, кто любит всегда добиваться ответа, оперируя изначальными условиями, не жульничая, а основывая решения на анализе, построение опять-таки логических связей. Эти качества, вынесенные со школьной скамьи, способны модулироваться и к взрослой серьезной жизни как в рабочих, так и в иных сложных моментах.

• Свойства
• Свойства в равнобедренных треугольниках
• Определение биссектрисы треугольника
• Определение длины
• Нахождение величины угла

Сегодня многие сталкиваются с проблемами при решении математических задач еще в начальной школе.

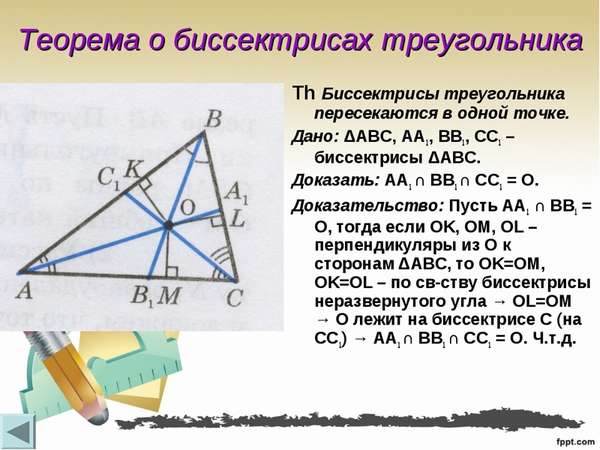
Однако даже те школьники, которые успешно осваивают первичную математическую программу, переходя на новый школьный и жизненный этап, где алгебра отделяется от геометрии, бывает, сталкиваются с серьезными затруднениями. Между тем, один раз выучив и, главное, поняв, как найти биссектрису треугольника, ученик навсегда запомнит эту формулу. Рассмотрим треугольник ABC с тремя проведенными биссектрисами. Как видно из рисунка, все они сходятся в одной точке.

Во-первых, определим, что биссектриса треугольника, и это одно из важнейших ее свойств, делит угол, из которого такой отрезок исходит, пополам. То есть в приведенном примере угол BAD равен углу DAC.

Это интересно: Как найти периметр треугольника.

Свойства

1. Биссектриса треугольника разделяет сторону, к которой она проведена на два отрезка, обладающие свойствами пропорциональности к сторонам, которые прилегают к каждому отрезку, соответственно. Таким образом, BD/CD = AB/AC.
2. Каждый треугольник способен обладать тремя данными отрезками. Другие значимые свойства касаются как частных, так и общих случаев конкретных рассматриваемых треугольников.

Свойства в равнобедренных треугольниках

1. Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
2. Разумеется, что будет верным и обратное свойство. То есть в равнобедренном треугольнике неизменно наблюдается равенство двух его биссектрис.
3. Из сказанного ранее вытекает вывод о том, что биссектриса, исходящая из противоположного основанию, служит также медианой и высотой.
4. Все биссектрисы равностороннего треугольника обладают равенством.

Определение биссектрисы треугольника

Допустим, что в рассматриваемом треугольнике ABC сторона AB = 5 cm, AC = 4 cm. Отрезок CD = 3 cm.

Определение длины

Определить длину можно по следующей формуле. AD = квадратный корень из разности произведения сторон и произведения пропорциональный отрезков.

Найдем длину стороны BC.

• Из свойств известно, что BD/CD = AB/AC.
• Значит, BD/CD = 5/4 = 1,25.
• BD/3 = 5/4.
• Значит, BD = 3,75.
• ABxAC = 54=20.
• CDxBD = 33,75 = 11,25.

Так, для того чтобы рассчитать длину, требуется вычесть из 20 11,25 и извлечь квадратный корень из получившегося 8,75. Результат с учетом тысячных долей получится 2,958.

Данный пример призван также эксплицитно указать на ситуацию, когда значения длины биссектрисы, как и все другие значения в математике, будут выражены не в натуральных числах, однако бояться этого не стоит.

Это интересно: в чем выражается эволюционный характер развития общества?

Нахождение величины угла

Для нахождения углов, образующихся биссектрисой, важно, прежде всего, помнить о сумме углов, неизменно составляющей 180 градусов. Предположим, что угол ABC равен 70 градусам, а угол BCA 50 градусам. Значит, путем простейших вычислений получим, что CAB = 180 (70+50) = 60 градусов.

Если использовать главное свойство, в соответствии с которым угол, из которого она исходит, делится пополам, получим равные значения углов BAD и CAD, каждый из которых будет 60/2 = 30 градусов.

Если требуется дополнительный наглядный пример, рассмотрим ситуацию, когда известен лишь угол BAD равный 28 градусам, а также угол ABC равный 70 градусам. Используя свойство биссектрисы, сразу найдем угол CAB путем умножения значения угла BAD на два. CAB = 282 =56. Значит, BAC = 180 (70+56) или 180 (70+282)= 180 126 = 54 градуса.

Специально не рассматривалась ситуация, когда данный отрезок выступает в качестве медианы или высоты, оставив для этого другие специализированные статьи.

Таким образом, мы рассмотрели такое понятие, как биссектриса треугольника, формула для нахождения длины и углов которой заложена и реализована в приведенных примерах, имеющих целью наглядно показать, каким образом можно использовать для решения тех или иных задач в геометрии. Также к данной теме относятся такие понятия, как медиана и высота. Если данный вопрос прояснился, следует обращаться к дальнейшему изучению различных других свойств треугольника, без которых немыслимо дальнейшее изучение геометрии.

Биссектриса треугольника

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

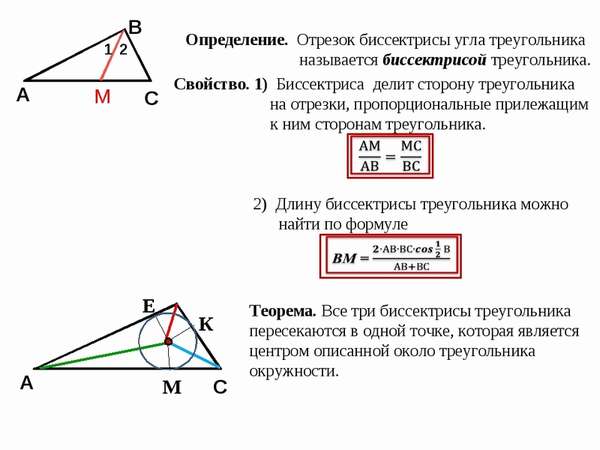
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

• CD – внутренняя биссектриса ∠ACB;
• CE – биссектриса угла, смежного с ∠ACB;
• ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Формулы для вычисления длины биссектрисы треугольника

Формулы для вычисления длины биссектрисы треугольника

Можно вывести различные формулы, с помощью которых можно вычислить длину биссектрисы треугольника, если известны:

· длины прилежащих сторон и угол между ними

· длины прилежащих сторон и отрезки, на которые биссектриса разбивает противолежащую сторону

· длины трех сторон треугольника.

Докажем первую из формул.

Задача 1. Вычислить длину биссектрисы треугольника, если известны длинны двух прилежащих сторон треугольника и угол между ними.

Решение. Пусть в треугольнике АВС известно, что

.

Обозначим биссектрису AD через la .

.

Используя формулу синуса двойного угла, получаем:

.

Ответ: .

Выражение называется средним гармоническим чисел а и с. Поэтому формулу можно запомнить следующим образом:

биссектриса треугольника равна произведению среднего гармонического прилежащих сторон треугольника на косинус половинного угла между ними.

Доказательство остальных формул можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».

Задача 2. Вычислите биссектрису треугольника ABC, проведённую из вершины А, если ВС = 18, АС = 15, АВ = 12.

Решение. Воспользуемся формулой для вычисления биссектрисы угла, если известны три стороны треугольника:

Задача 3. Определить площадь треугольника, если две его стороны равны 35 см и 14 см, а биссектриса угла между ними содержит 12 см.

Пусть в треугольнике АВС АС=35, АВ=14, AD – биссектриса, AD=12.

,

Вычислим , получаем:

, .

(по основному тригонометрическому тождеству).

Далее по формуле синуса двойного угла вычисляем

.

Для вычисления площади треугольника воспользуемся формулой .

Задача 4. . В равнобедренном треугольнике BCD с основанием BD

проведена биссектриса BE. Известно, что СЕ = 20 и DE = 10. Найдите BE.

Используя свойство биссектрисы угла треугольника (урок 4), получаем

, то есть .

Таким образом, нам известны длины двух прилежащих сторон и отрезки, на которые биссектриса разбивает противолежащую сторону, поэтому

Ответ :.

Задачи для самостоятельного решения

1. Дан треугольник со сторонами 4, 8, 9. Найти длину биссектрисы, проведенной к большей стороне.

2. В треугольнике ABC известно, что АВ = 10, АС = 15, BAC = 120°. Найдите биссектрису AD.

3. Катеты прямоугольного треугольника равны 6 и 8. Найдите биссектрису треугольника, проведённую из вершины прямого угла.

4. В равнобедренном треугольнике BCD с основанием BD проведена биссектриса BE. Известно, что СЕ = 18 и DE = 12. Найдите BE.

[spoiler title=”источники:”]

http://pandia.ru/text/78/654/11234.php

[/spoiler]

Математика, как известно, царица наук. Неслучайно это выражение так любят учителя, особенно старой формации. Математика открывается исключительно тем, кто умеет, во-первых, логически мыслить, а во-вторых, тем, кто любит всегда добиваться ответа, оперируя изначальными условиями, не жульничая, а основывая решения на анализе, построение опять-таки логических связей. Эти качества, вынесенные со школьной скамьи, способны модулироваться и к взрослой серьезной жизни как в рабочих, так и в иных сложных моментах.

Оглавление:

• Свойства
• Свойства в равнобедренных треугольниках
• Определение биссектрисы треугольника
• Определение длины
• Нахождение величины угла

Сегодня многие сталкиваются с проблемами при решении математических задач еще в начальной школе.

Однако даже те школьники, которые успешно осваивают первичную математическую программу, переходя на новый школьный и жизненный этап, где алгебра отделяется от геометрии, бывает, сталкиваются с серьезными затруднениями. Между тем, один раз выучив и, главное, поняв, как найти биссектрису треугольника, ученик навсегда запомнит эту формулу. Рассмотрим треугольник ABC с тремя проведенными биссектрисами. Как видно из рисунка, все они сходятся в одной точке.

Во-первых, определим, что биссектриса треугольника, и это одно из важнейших ее свойств, делит угол, из которого такой отрезок исходит, пополам. То есть в приведенном примере угол BAD равен углу DAC.

Это интересно: Как найти периметр треугольника.

Свойства

1. Биссектриса треугольника разделяет сторону, к которой она проведена на два отрезка, обладающие свойствами пропорциональности к сторонам, которые прилегают к каждому отрезку, соответственно. Таким образом, BD/CD = AB/AC.
2. Каждый треугольник способен обладать тремя данными отрезками. Другие значимые свойства касаются как частных, так и общих случаев конкретных рассматриваемых треугольников.

Свойства в равнобедренных треугольниках

1. Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
2. Разумеется, что будет верным и обратное свойство. То есть в равнобедренном треугольнике неизменно наблюдается равенство двух его биссектрис.
3. Из сказанного ранее вытекает вывод о том, что биссектриса, исходящая из противоположного основанию, служит также медианой и высотой.
4. Все биссектрисы равностороннего треугольника обладают равенством.

Определение биссектрисы треугольника

Допустим, что в рассматриваемом треугольнике ABC сторона AB = 5 cm, AC = 4 cm. Отрезок CD = 3 cm.

Определение длины

Определить длину можно по следующей формуле. AD = квадратный корень из разности произведения сторон и произведения пропорциональный отрезков.

Найдем длину стороны BC.

• Из свойств известно, что BD/CD = AB/AC.
• Значит, BD/CD = 5/4 = 1,25.
• BD/3 = 5/4.
• Значит, BD = 3,75.
• ABxAC = 54=20.
• CDxBD = 33,75 = 11,25.

Так, для того чтобы рассчитать длину, требуется вычесть из 20 11,25 и извлечь квадратный корень из получившегося 8,75. Результат с учетом тысячных долей получится 2,958.

Данный пример призван также эксплицитно указать на ситуацию, когда значения длины биссектрисы, как и все другие значения в математике, будут выражены не в натуральных числах, однако бояться этого не стоит.

Это интересно: в чем выражается эволюционный характер развития общества?

Нахождение величины угла

Для нахождения углов, образующихся биссектрисой, важно, прежде всего, помнить о сумме углов, неизменно составляющей 180 градусов. Предположим, что угол ABC равен 70 градусам, а угол BCA 50 градусам. Значит, путем простейших вычислений получим, что CAB = 180 (70+50) = 60 градусов.

Если использовать главное свойство, в соответствии с которым угол, из которого она исходит, делится пополам, получим равные значения углов BAD и CAD, каждый из которых будет 60/2 = 30 градусов.

Если требуется дополнительный наглядный пример, рассмотрим ситуацию, когда известен лишь угол BAD равный 28 градусам, а также угол ABC равный 70 градусам. Используя свойство биссектрисы, сразу найдем угол CAB путем умножения значения угла BAD на два. CAB = 282 =56. Значит, BAC = 180 (70+56) или 180 (70+282)= 180 126 = 54 градуса.

Специально не рассматривалась ситуация, когда данный отрезок выступает в качестве медианы или высоты, оставив для этого другие специализированные статьи.

Таким образом, мы рассмотрели такое понятие, как биссектриса треугольника, формула для нахождения длины и углов которой заложена и реализована в приведенных примерах, имеющих целью наглядно показать, каким образом можно использовать для решения тех или иных задач в геометрии. Также к данной теме относятся такие понятия, как медиана и высота. Проведите ночь в компании красивой проститутки СПБ . Посетите наш онлайн-портал, и вы обнаружите подборку самых способных девушек своего города. Изучите все доступные варианты, и мы посодействуем вам в выборе подходящей спутницы! Если данный вопрос прояснился, следует обращаться к дальнейшему изучению различных других свойств треугольника, без которых немыслимо дальнейшее изучение геометрии.

Биссектриса треугольника

В данной публикации мы рассмотрим основные свойства биссектрисы равнобедренного треугольника (внутренней и внешней), а также разберем пример решения задачи по данной теме.

Примечание: напомним, что равнобедренным называется треугольник, в котором две стороны равны (боковые), а третья является основание фигуры.

Свойства биссектрисы равнобедренного треугольника

Свойство 1

В равнобедренном треугольнике биссектрисы, проведенные к боковым сторонам, равны между собой.

• AB = BC, т.к. являются боковыми сторонами равнобедренного △ABC;
• AF = CG, т.к. это биссектрисы, проведенные к боковым сторонам треугольника (или биссектрисы углов BAC и ACB, которые также равны между собой).

Обратная формулировка: если две из трех биссектрис в треугольнике равны, значит он является равнобедренным.

Свойство 2

В равнобедренном треугольнике биссектриса, проведенная к основанию, одновременно является и медианой и высотой.

• BH – биссектриса угла ABC, проведенная к основанию AC;
• BH – медиана, значит она делит AC пополам, т.е. AH = HC;
• BH – высота, следовательно, она перпендикулярна AC.

Свойство 3

Если известны стороны равнобедренного треугольника, то длину биссектрисы, проведенную к основанию, можно посчитать по формуле:

l² = b² – a²

• l – биссектриса;
• b – боковая сторона;
• a – половина основания.

Примечание: данная формула следует из теоремы Пифагора (l и a – катеты прямоугольного треугольника, b – его гипотенуза).

Свойство 4

Внешняя биссектриса угла равнобедренного треугольника, расположенного напротив его основания, параллельна этому основанию.

• BD – внешняя биссектриса ∠ABC треугольника;
• BD параллельна основанию AC.

Примечание: к равнобедренному треугольнику применимы и другие свойства биссектрисы, приведенные в нашей публикации – “Определение и свойства биссектрисы угла треугольника”.

Пример задачи

Биссектриса равнобедренного треугольника с боковой стороной 25 см равняется 20 см. Найдите периметр фигуры.

Решение
Воспользуемся формулой, приведенной в Свойстве 3, чтобы найти длину основания.
a² = b² – l² = 25² – 20² = 225.

Извлекаем квадратный корень из найденного значения и получаем 15 см.
Следовательно, основание треугольника равно 30 см (15 см ⋅ 2).

Периметр фигуры равен сумме всех ее сторон, т.е.: 25 см + 25 см + 30 см = 80 см.

Как найти биссектрису равнобедренного треугольника

У равнобедренного треугольника две стороны равны, углы при его основании тоже будут равны. Поэтому биссектрисы, проведенные к боковым сторонам, будут равны друг другу. Биссектриса, проведенная к основанию равнобедренного треугольника, будет одновременно медианой и высотой этого треугольника.

Инструкция

Пусть биссектриса AE проведена к основанию BC равнобедренного треугольника ABC. Треугольник AEB будет прямоугольным, так как биссектриса AE будет одновременно являться его высотой. Боковая сторона AB будет гипотенузой этого треугольника, а BE и AE – его катетами.По теореме Пифагора (AB^2) = (BE^2)+(AE^2). Тогда (BE^2) = sqrt((AB^2)-(AE^2)). Так как AE и медиана треугольника ABC, то BE = BC/2. Следовательно, (BE^2) = sqrt((AB^2)-((BC^2)/4)).Если задан угол при основании ABC, то из прямоугольного треугольника биссектриса AE равна AE = AB/sin(ABC). Угол BAE = BAC/2, так как AE – биссектриса. Отсюда, AE = AB/cos(BAC/2).

Пусть теперь проведена высота BK к боковой стороне AC. Эта высота уже не является ни медианой, ни биссектрисой треугольника. Для вычисления ее длины существует равен половине суммы длин всех его сторон: P = (AB+BC+AC)/2 = (a+b+c)/2, где BC = a, AC = b, AB = c.Формула Стюарта для длины биссектрисы, проведенной к стороне c (то есть, AB), будет иметь вид: l = sqrt(4abp(p-c))/(a+b).

Из формулы Стюарта видно, что биссектриса, проведенная к стороне b (AC), будет иметь такую же длину, так как b = c.

Источники:

• Медианы, биссектрисы и высоты треугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?