Найдите большую диагональ правильного шестиугольника, периметр которого 36 см.
На этой странице вы найдете ответ на вопрос Найдите большую диагональ правильного шестиугольника, периметр которого 36 см?. Вопрос
соответствует категории Геометрия и уровню подготовки учащихся 10 – 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.
Правильным шестиугольником называется шестиугольник, у которого все стороны и углы равны. Правильный шестиугольник обладает следующими свойствами.
– Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
– Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.
– Меньшая диагональ правильного шестиугольника в раз больше его стороны.
– Угол между сторонами правильного шестиугольника равен 120°.
– Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.
– Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник – это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник – это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник – это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 – 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt <3>) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
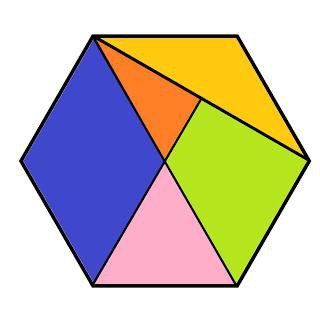
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .
Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :
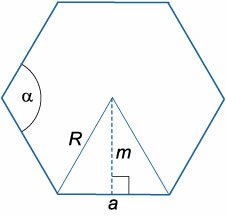
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac<<sqrt 3 >><2>
ormalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac<<3sqrt 3 >><2>
ormalsize),
где (p) − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Правильным шестиугольником называется выпуклый многоугольник с шестью одинаковыми сторонами и шестью углами.
Внутренние углы в правильном шестиугольнике равны (120^circ):
(alpha = 120^circ)
Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
(m = alargefrac >
ormalsize)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac >
ormalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
(R = a)
Периметр правильного шестиугольника
(P = 6a)
Площадь правильного шестиугольника
(S = pr = largefrac >
ormalsize),
где (p) − полупериметр шестиугольника.
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
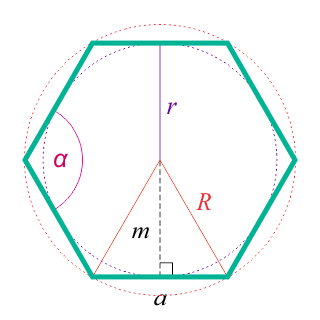
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3 ) 2 = 37,68 (см 2 ).
Осталось сосчитать объем: V = 37, 68 * 4 = 150,72 (см 3 ).
Ответ. V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Правильный многоугольник
Правильный многоугольник — это многоугольник, все стороны и углы которого равны.
Вокруг правильного многоугольника можно описать окружность и в него можно вписать окружность. Центры этих окружностей совпадают.
Правильный шестиугольник
Правильный шестиугольник – это шестиугольник, все стороны и углы которого равны.
Описанный многоугольник
Если все стороны многоугольника касаются некоторой окружности , то он называется описанным многоугольником .
Шестиугольник представляет собой геометрическую фигуру, многоугольник, который имеет шесть углов и
шесть сторон.
Также существует правильный шестиугольник. Он обладает следующим свойством: все ребра и углы равны.
Каждый угол составляет 120 градусов. А также он состоит из шести правильных и равных
треугольников.
- Длинная диагональ правильного шестиугольника через
площадь - Котроткая диагональ правильного шестиугольника через
площадь - Длинная диагональ правильного шестиугольника через
сторону - Короткая диагональ правильного шестиугольника через
сторону
Длинная диагональ через площадь
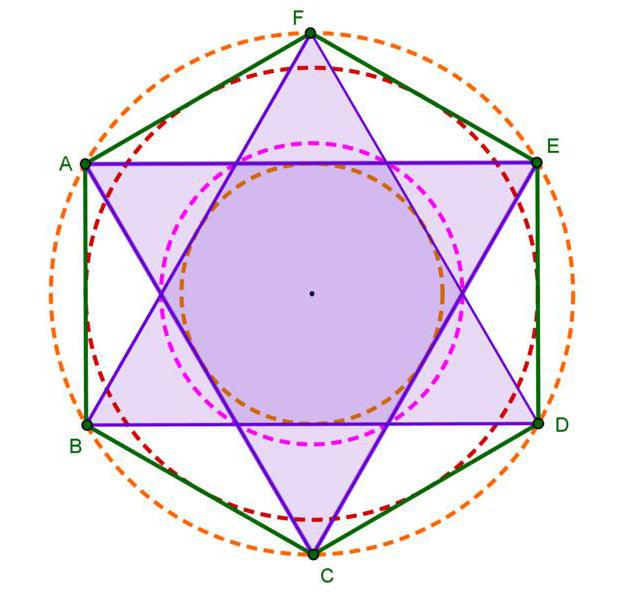
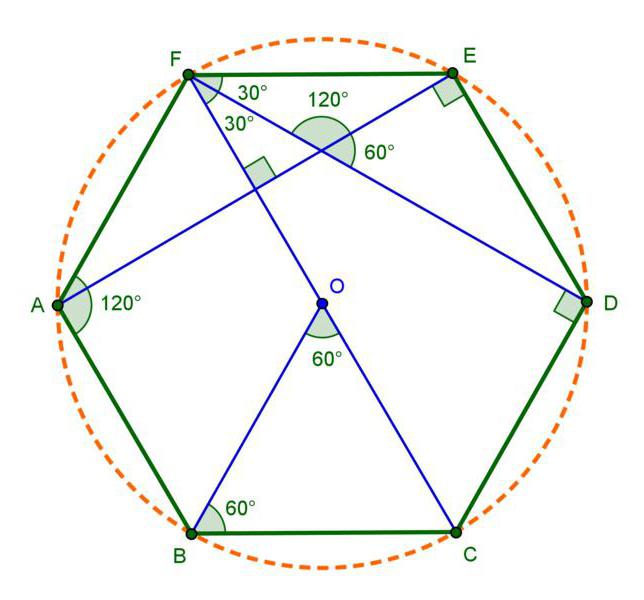
Длинной диагональю на рисунке являются отрезки ВЕ, AD и CF. Все диагонали будут равны между собой.
Это свойство касается как правильной фигуры, так и неправильной. Для нахождения длинной диагонали
правильного шестиугольника понадобится площадь полной фигуры (правильного шестиугольника), которую
можно найти по формуле S = (a * a * √3 * 6) / 4. А диагональ находится по
следующим образом:
D = √((S / 3√3) * 8)
где S — площадь правильного шестиугольника.
Цифр после
запятой:
Результат в:
Пример. Сторона шестиугольника равна 6 см. Тогда площадь: S = (6 * 6 * √3 * 6) / 4 = 54√3 см. D = √((54√3 / 3√3) * 8) = 12 см.
Короткая диагональ через площадь
Короткими диагоналями можно назвать BD, BF, AE или же DF. Для нахождения неизвестной стороны также,
как и в прошлой ситуации, понадобится площадь фигуры, которую возможно найти по следующей формуле:
S = (a * a * √3 * 6) / 4. После этого найденная величина подставляется в
готовую формулу:
D = √((S / √3) * 2)
где S — площадь правильного многоугольника.
Цифр после
запятой:
Результат в:
Пример. Как и в прошлой задаче, ребро равно 6 см. Тогда площадь правильного
шестиугольника = 54√3 см. Далее можно находить и искомую диагональ: D = √((54√3 / √3) * 2) = 6√3
Длинная диагональ через сторону
Длинной диагональю на рисунке являются отрезки ВЕ, AD и CF. Длинную диагональ правильно
шестиугольника можно вычислить и без нахождения площади. Для выполнения математических действий и
нахождения неизвестной переменной надо знать лишь ребро многоугольника:
D = 2a
где a — сторона правильного шестиугольника.
Цифр после
запятой:
Результат в:
Длинная диагональ состоит из двух сторон треугольников, прилегающих друг к другу, поэтому сторону
умножаем на 2.
Пример. В задаче дан правильный шестиугольник. Его ребро равно 3 см. Тогда длинная
диагональ равна 6 см.
Короткая диагональ через сторону
Также существует и другой способ нахождения короткой диагонали, равностороннего шестиугольника.
Например, диагонали BD. Для нахождения достаточно лишь знание стороны фигуры:
D = √(3 * a * a)
где a — сторона правильного шестиугольника.
Цифр после
запятой:
Результат в:
Пример. Сторона АВ равна 10 см. Тогда BD = D = √(3 * 10 * 10) = 10√3 см = 17 см.
Для более простого понимания такой темы, как вычисление диагонали правильного шестиугольника, стоит
для начала увидеть, что данный многоугольник состоит из шести равносторонних и равных между собой
треугольников. (Неправильный шестиугольник условно можно разделить на шесть равнобедренных
треугольник). О – это центр правильного шестиугольника. Он делит диагонали на равные отрезки. Также
точка пересечения длинных диагоналей является центром вписанной и описанных окружностей. Все
диагонали также равны между собой и делят углы на две равные части, то есть выполняют функцию
биссектрисы, а также высоты или медианы, так как были проведены в равнобедренном треугольнике. Таким
образом будет легче находить какие-то неизвестные отрезки.
Однако существует и более сложный метод – через нахождение площади фигуры. Данную формулу запомнить
просто: S = (a * a * √3) / 4 – она необходима, чтобы вычислить площадь
равностороннего треугольника, где величина а является стороной. А вышеупомянутая фигура состоит из
шести таких геометрических фигур, поэтому конечная формула будет выглядеть так: S = (a * a * √3 * 6) / 4
Таким образом, шестиугольник является не такой уж и сложной фигурой, как кажется на первый взгляд.
Достаточно изучить элементарные свойства и запомнить их.
Найдите правильный ответ на вопрос ✅ «В правильном шестиугольнике сторона равна 10 см. Найти наибольшую диагональ этого шестиугольника. …» по предмету 📘 Геометрия, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Дано треугольник OBS угол B=90 градусов угол S=45 градусов OB=1008 СМ Найти SB
Ответы (1)
Дано abcd-параллелограмм, BCA=31 градусов, BAC=25 градусов
Ответы (1)
Один угол параллелограмма в 4 разОдин угол параллелограмма в 4 раза больше другого. Найдите больший угол. Ответ дайте в градусах. а больше другого. Найдите больший угол.
Ответы (1)
NK на 19 см. больше MN, MK = 81 см. Найти : MK, NK
Ответы (1)
Начертите угол AOB и лучи ОК и ОМ, проходящие между сторонами этого угла, так, чтобы угол AOB = 90, AOK = 40, MOB = 30, Найдите KOM
Ответы (1)
Главная » Геометрия » В правильном шестиугольнике сторона равна 10 см. Найти наибольшую диагональ этого шестиугольника.
UCHEES.RU – помощь студентам и школьникам
В 17:49 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
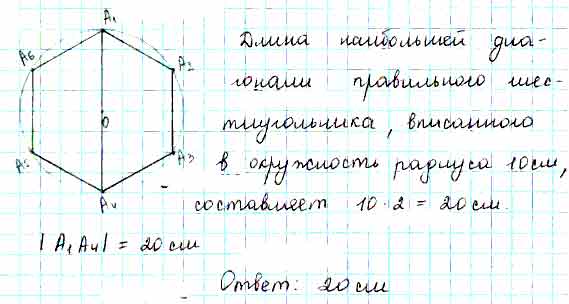
Чему равна длина наибольшей диагонали правильного шестиугольника, вписанного в окружность радиуса 10 см?
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике “ЕГЭ (школьный)”. Ваш вопрос звучал следующим образом: Чему равна длина наибольшей диагонали правильного шестиугольника, вписанного в окружность радиуса 10 см?
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
решение к заданию по математике
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Брагина Гера Куприяновна – автор студенческих работ, заработанная сумма за прошлый месяц 58 559 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
2020 – 2023 – UCHEES.RU