Максимальная площадь четырехугольника
Для четырех сторон четырехугольника a, b, c, d найдите максимально возможную площадь четырехугольника от заданных сторон.
Согласно формуле Бретшнейдера , площадь общего четырехугольника определяется как
Здесь a, b, c, d — стороны четырехугольника, s — полупериметр четырехугольника, а углы — два противоположных угла.
Таким образом, эта формула максимизируется только тогда, когда противоположные углы суммируются с пи (180), тогда мы можем использовать упрощенную форму формулы Бретшнейдера, чтобы получить (максимальную) площадь K.
Эта формула называется формулой Брахмагупты .
Ниже приведена реализация данного подхода
// Программа CPP, чтобы найти максимум
// четырехугольник
#include
using namespace std;
double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return sqrt ((semiperimeter – a) *
double a = 1, b = 2, c= 1, d = 2;
printf ( “%.2fn” ,maxArea(a, b, c, d));
// Java-программа для поиска максимального значения
// четырехугольник
static double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2 ;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return Math.sqrt((semiperimeter – a) *
public static void main (String[] args)
double a = 1 , b = 2 , c= 1 , d = 2 ;
System.out.println(maxArea(a, b, c, d));
// Этот код предоставлен sunnysingh
# Python3 программа для поиска максимума
# площадь четырехугольника
def maxArea (a , b , c , d ):
semiperimeter = (a + b + c + d) / 2
# Применение формулы Брахмагупты к
# получить максимальную площадь четырехугольника
return math.sqrt((semiperimeter – a) *
print ( “%.2f” % maxArea(a, b, c, d))
# Этот код предоставлен “Sharad_Bhardwaj”.
// C # программа для поиска максимума
// четырехугольник
static double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return Math.Sqrt((semiperimeter – a) *
public static void Main ()
double a = 1, b = 2, c= 1, d = 2;
Console.WriteLine(maxArea(a, b, c, d));
// Этот код предоставлен vt_m.
// PHP-программа, чтобы найти максимум
// четырехугольник
function maxArea( $a , $b , $c , $d )
$semiperimeter = ( $a + $b + $c + $d ) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return sqrt(( $semiperimeter – $a ) *
$a = 1; $b = 2; $c = 1; $d = 2;
echo (maxArea( $a , $b , $c , $d ));
// Этот код предоставлен vt_m.
?>
Площади четырехугольников
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
a и b – смежные стороны
d – диагональ,
φ – любой из четырёх углов между диагоналями
Получается из верхней формулы подстановкой d=2R
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
a – сторона,
ha – высота, опущенная на эту сторону
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
a – сторона,
ha – высота, опущенная на эту сторону
a – сторона,
φ – любой из четырёх углов ромба
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
a и b – основания,
c и d – боковые стороны
a и b – неравные стороны,
φ – угол между ними
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,
Формулу называют «Формула Брахмагупты»
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник |  |
S = ab | |
 |
|||
 |
|||
| Параллелограмм |  |
||
 |
|||
 |
|||
| Квадрат |  |
S = a 2 | |
 |
S = 4r 2 | ||
 |
|||
 |
|||
| Ромб |  |
||
 |
|||
 |
|||
 |
|||
 |
|||
| Трапеция |  |
||
 |
S = m h | ||
 |
|||
 |
|||
| Дельтоид |  |
S = ab sin φ | |
 |
 |
||
 |
|||
 |
|||
| Произвольный выпуклый четырёхугольник |  |
||
| Вписанный четырёхугольник |  |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
| Прямоугольник | |
 |
|
 |
|
 |
|
| Параллелограмм | |
 |
|
 |
|
 |
|
| Квадрат | |
 |
S = a 2
где |
 |
S = 4r 2 |
 |
|
 |
|
| Ромб | |
 |
|
 |
|
 |
|
 |
|
 |
|
| Трапеция | |
 |
|
 |
|
 |
|
 |
|
| Дельтоид | |
 |
|
 |

где |
 |
|
 |
|
| Произвольный выпуклый четырёхугольник | |
 |
|
| Вписанный четырёхугольник | |
 |
| Прямоугольник |
 |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
Параллелограмм
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Квадрат
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
Ромб
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
Трапеция
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны ,
Дельтоид
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
Произвольный выпуклый четырёхугольник
φ – любой из четырёх углов между ними
Вписанный четырёхугольник
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
Найти наибольшую площадь четырехугольника
На сторонах AD и BC параллелограмма ABCD взяты соответственно точки M и N, причём M — середина AD, а BN : NC = 1 : 3.
а) Докажите, что прямые AN и AC делят отрезок BM на три равные части.
б) Найдите площадь четырёхугольника, вершины которого находятся в точках С, N и точках пересечения прямой BM c прямыми AN и AC, если площадь параллелограмма ABCD равна 48.
а) Обозначим точки пересечения прямой BM c прямыми AN и AC буквами P и R соответственно.
Пусть O – точка пересечения диагоналей параллелограмма. Тогда AO и BM — медианы треугольника ABD, значит,
Из подобия треугольников BPN и MPA находим, что
Значит, Из доказанного следует, что BP=PR=RM.
б) Пусть площадь параллелограмма равна S. Из подобия треугольников MRA и BRC с коэффициентом следует, что высота треугольника BRC, проведённая к стороне BC, составляет высоты параллелограмма, проведённой к той же стороне. Следовательно, площадь треугольника BRC равна
Аналогично найдём площадь треугольника BNP. Его высота, проведённая к BN, составляет высоты параллелограмма, проведённой к стороне BC сама сторона BN в четыре раза меньше стороны параллелограмма BC. Поэтому
Следовательно, площадь четырёхугольника PRCN равна
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б)
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки |
2 |
| Имеется верное доказательство утверждения пункта а)
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, [spoiler title=”источники:”] http://www.resolventa.ru/spr/planimetry/sqf.htm http://math-ege.sdamgia.ru/problem?id=504418 [/spoiler] |
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given four sides of quadrilateral a, b, c, d, find the maximum area of the quadrilateral possible from the given sides .
Examples:
Input : 1 2 1 2 Output : 2.00 It is optimal to construct a rectangle for maximum area .
According to Bretschneider’s formula, the area of a general quadrilateral is given by
Here a, b, c, d are the sides of a quadrilateral, s is the semiperimeter of a quadrilateral and angles are two opposite angles.
So, this formula is maximized only when opposite angles sum to pi(180) then we can use a simplified form of Bretschneider’s formula to get the (maximum) area K.
This formula is called as Brahmagupta’s formula .
Below is the implementation of given approach
C++
#include <iostream>
#include <math.h>
using namespace std;
double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
int main()
{
double a = 1, b = 2, c= 1, d = 2;
cout <<maxArea(a, b, c, d);
return 0;
}
C
#include <stdio.h>
#include <math.h>
double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
int main()
{
double a = 1, b = 2, c= 1, d = 2;
printf("%.2fn",maxArea(a, b, c, d));
return 0;
}
Java
import java.io.*;
class GFG
{
static double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return Math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
public static void main (String[] args)
{
double a = 1, b = 2, c= 1, d = 2;
System.out.println(maxArea(a, b, c, d));
}
}
Python3
import math
def maxArea (a , b , c , d ):
semiperimeter = (a + b + c + d) / 2
return math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d))
a = 1
b = 2
c = 1
d = 2
print("%.2f"%maxArea(a, b, c, d))
C#
using System;
class GFG {
static double maxArea(double a, double b,
double c, double d)
{
double semiperimeter = (a + b + c + d) / 2;
return Math.Sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
public static void Main ()
{
double a = 1, b = 2, c= 1, d = 2;
Console.WriteLine(maxArea(a, b, c, d));
}
}
PHP
<?php
function maxArea( $a, $b, $c, $d)
{
$semiperimeter = ($a + $b + $c + $d) / 2;
return sqrt(($semiperimeter - $a) *
($semiperimeter - $b) *
($semiperimeter - $c) *
($semiperimeter - $d));
}
$a = 1; $b = 2; $c= 1; $d = 2;
echo(maxArea($a, $b, $c, $d));
?>
Javascript
<script>
function maxArea(a, b, c, d)
{
let semiperimeter = (a + b + c + d) / 2;
return Math.sqrt((semiperimeter - a) *
(semiperimeter - b) *
(semiperimeter - c) *
(semiperimeter - d));
}
let a = 1, b = 2, c= 1, d = 2;
document.write(maxArea(a, b, c, d));
</script>
Output:
2.00
Time Complexity: O(logn)
Auxiliary Space: O(1)
Please suggest if someone has a better solution which is more efficient in terms of space and time.
This article is contributed by Aarti_Rathi. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
Last Updated :
22 Jun, 2022
Like Article
Save Article
Как найти максимальную площадь четырехугольника
Яхуб нарисовал множество из n точек на декартовой плоскости. Он назвал их «особыми точками». Четырехугольник — это многоугольник без самопересечений, имеющий четыре стороны (или ребра) и четыре вершины (или угла). Пожалуйста, обратите внимание, что четырехугольник может не быть выпуклым. Особый четырехугольник — это такой четырехугольник, в котором все четыре вершины принадлежат множеству особых точек. Вам дано множество особых точек. Пожалуйста, вычислите максимальную площадь особого четырехугольника.
В первой строке записано целое число n ( 4 ≤ n ≤ 300 ). В каждой из следующих n строк записано по два целых числа: x i, y i ( — 1000 ≤ x i, y i ≤ 1000) — декартовы координаты i -той особой точки. Гарантируется, что никакие три точки не лежат на одной прямой. Гарантируется, что никакие две точки не совпадают.
Выведите единственное вещественное число — максимальную площадь особого четырехугольника. Ответ будет считаться правильным, если его относительная или абсолютная погрешность не превышает 10 — 9 .
Максимальная площадь четырехугольника
Для четырех сторон четырехугольника a, b, c, d найдите максимально возможную площадь четырехугольника от заданных сторон.
Согласно формуле Бретшнейдера , площадь общего четырехугольника определяется как 
Здесь a, b, c, d — стороны четырехугольника, s — полупериметр четырехугольника, а углы — два противоположных угла.
Таким образом, эта формула максимизируется только тогда, когда противоположные углы суммируются с пи (180), тогда мы можем использовать упрощенную форму формулы Бретшнейдера, чтобы получить (максимальную) площадь K.
Эта формула называется формулой Брахмагупты .
Ниже приведена реализация данного подхода
// Программа CPP, чтобы найти максимум
// четырехугольник
#include
using namespace std;
double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return sqrt ((semiperimeter — a) *
double a = 1, b = 2, c= 1, d = 2;
printf ( «%.2fn» ,maxArea(a, b, c, d));
// Java-программа для поиска максимального значения
// четырехугольник
static double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2 ;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return Math.sqrt((semiperimeter — a) *
public static void main (String[] args)
double a = 1 , b = 2 , c= 1 , d = 2 ;
System.out.println(maxArea(a, b, c, d));
// Этот код предоставлен sunnysingh
# Python3 программа для поиска максимума
# площадь четырехугольника
def maxArea (a , b , c , d ):
semiperimeter = (a + b + c + d) / 2
# Применение формулы Брахмагупты к
# получить максимальную площадь четырехугольника
return math.sqrt((semiperimeter — a) *
print ( «%.2f» % maxArea(a, b, c, d))
# Этот код предоставлен «Sharad_Bhardwaj».
// C # программа для поиска максимума
// четырехугольник
static double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return Math.Sqrt((semiperimeter — a) *
public static void Main ()
double a = 1, b = 2, c= 1, d = 2;
Console.WriteLine(maxArea(a, b, c, d));
// Этот код предоставлен vt_m.
// PHP-программа, чтобы найти максимум
// четырехугольник
function maxArea( $a , $b , $c , $d )
$semiperimeter = ( $a + $b + $c + $d ) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return sqrt(( $semiperimeter — $a ) *
$a = 1; $b = 2; $c = 1; $d = 2;
echo (maxArea( $a , $b , $c , $d ));
// Этот код предоставлен vt_m.
?>
Формулы вычисления площади произвольного четырёхугольника
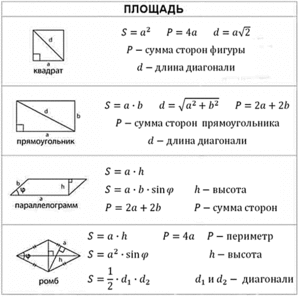
В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.
Определения и соглашения
В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
- Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
- Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
- Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
- Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
- Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
- Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
- Угол между сторонами a и b будем обозначать следующей записью (a,b).
Нахождение площади четырёхугольника различными способами и методами
Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).
Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.
Теперь пусть даны стороны и противолежащие углы четырёхугольника.
Пусть a, b, c, d известные стороны многоугольника; p — его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).
На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.
Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.
Подставим полученные данные в нашу формулу, получим: S = rad((40 — 18)*(40 — 23)*(40 — 22)*(40 — 17) — 18*23*22*17*0,97) = rad(22*17*18*23 — 18*23*22*17*1/4) = rad((22*17*18*23*(1 — 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.
Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.
Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:
Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:
S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.
Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.
Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:
S = rad((65 — 26)*(65 — 35)*(65 — 39)*(65 — 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.
Заключение
Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов — квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:
- S = 1/2*d1*d2*sin(d1,d2);
- S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
- S = ((a + b+ c + d)/2)*r
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.
Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.
Видео
Разобраться в этой теме вам поможет видео.
источники:
http://espressocode.top/maximum-area-quadrilateral/
http://liveposts.ru/articles/education-articles/matematika/formuly-vychisleniya-ploshhadi-proizvolnogo-chetyryohugolnika
Сообщения без ответов | Активные темы | Избранное
|
|
Какую наибольшую площадь может иметь четырёхугольник?
|
|
01/12/11 |
Какую наибольшую площадь может иметь четырёхугольник, три последовательные стороны которого соответственно равны
|
|
|
|
|
waxtep |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
|
07/01/16 |
|
|
|
|
|
Fedorov |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
|
29/06/10 |
|
|
|
|
|
wrest |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
|
05/09/16 |
|
|
|
|
|
waxtep |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
|
07/01/16 |
Кстати, а зачем вы написали “с меньшим основанием”? Вроде б, диагональ, выходящая из вершины-пересечения Я имел в виду, что второе основание трапеции, которое , формУлами, геометрический факт увидел уже из них, из
|
|
|
|
|
wrest |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
|
05/09/16 |
waxtep Ах, ну да – “основанием”, не “стороной”
|
|
|
|
|
waxtep |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
|
07/01/16 |
из очипятка, правильно А можно ли построить искомую фигуру циркулем и линейкой без делений? ой, в этом я слаб. Вообще конечно геометрические решение было бы интересно понять; в предельном случае
|
|
|
|
|
Fedorov |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
|
29/06/10 |
А можно ли построить искомую фигуру циркулем и линейкой без делений? Отрезки
|
|
|
|
|
svv |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
||
23/07/08 |
|||
|
|
|||
|
ИСН |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
||
18/05/06 |
Не очень интересно, что
|
||
|
|
|||
|
g______d |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
||
08/11/11 |
Пусть Дальше не очень интересно, я думаю. — Вс, 14 апр 2019 14:21:54 — svv , я не заметил Вашего ответа, но удалять уже не буду.
|
||
|
|
|||
|
Fedorov |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
|
29/06/10 |
|
|
|
|
|
wrest |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
|
05/09/16 |
|
|
|
|
|
svv |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
||
23/07/08 |
|||
|
|
|||
|
wrest |
Re: Какую наибольшую площадь может иметь четырёхугольник?
|
|
05/09/16 |
То же для угла А, точно – и отсюда следует что искомый четырехугольник — именно трапеция, плюс по условию она получается равнобедренная. Вернее, из-за равнобедренности, с учетом равенства этих углов (
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Из всех четырехугольников вписанных в окружности найдите четырехугольник наибольшей площади.
santa maria
Ученик
(74),
закрыт
6 лет назад
Семен Аркадьевич
Высший разум
(340149)
8 лет назад
А что тут искать? Площадь четырехугольника равна половине произведения диагоналей на синус угла между ними. Максимальная величина синуса =1 . Это угол 90 градусов.
Максимальная диагональ – это диаметр окружности. Значит из всех четырехугольников вписанных в окружность максимальную площадь имеет вписанный КВАДРАТ.






























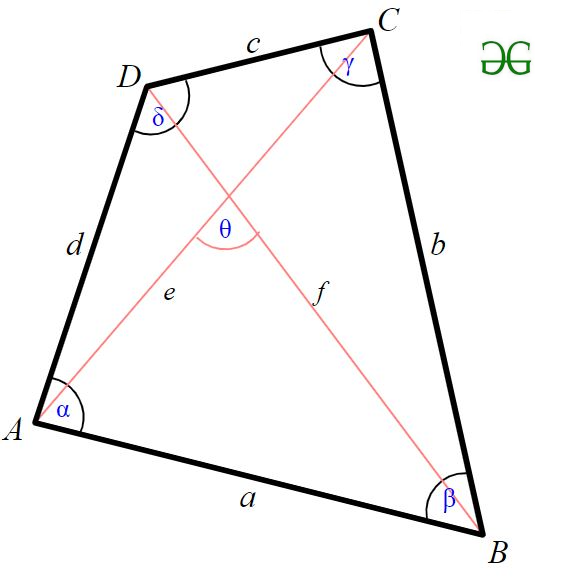

 Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
 ?
? и
и  , должна быть перпендикулярна стороне
, должна быть перпендикулярна стороне  , больше чем
, больше чем 

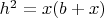 конечно
конечно получается равнобедренный прямоугольный треугольник, а в трапеции этот прямой угол как бы “разъезжается” на два…
получается равнобедренный прямоугольный треугольник, а в трапеции этот прямой угол как бы “разъезжается” на два…
 . Вот если даны три стороны
. Вот если даны три стороны  – тогда что? Какой должна быть четвёртая, и транслируется ли это в какое-то простое геометрическое свойство?
– тогда что? Какой должна быть четвёртая, и транслируется ли это в какое-то простое геометрическое свойство? ,
,  ,
,  . Пусть задан угол
. Пусть задан угол  . Поскольку
. Поскольку  и
и  таким образом известны и угол
таким образом известны и угол  можно выбирать произвольно, можно считать, что он прямой (это максимизирует площадь треугольника
можно выбирать произвольно, можно считать, что он прямой (это максимизирует площадь треугольника  при остальных параметрах фиксированных). Таким образом, нужно максимизировать функцию
при остальных параметрах фиксированных). Таким образом, нужно максимизировать функцию
 .
. ) получается что это трапеция.
) получается что это трапеция.