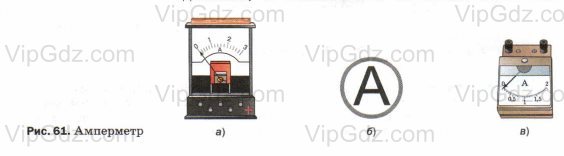
Рассмотрите амперметры, данные на рисунках 61, 62. Определите цену деления шкалы каждого амперметра. Какую наибольшую силу тока они могут измерять? Перерисуйте шкалу амперметра (см. рис. 61, а) в тетрадь и покажите, каково будет положение стрелки при силе тока 0,3 А и 1,5 А.
Другие задачи из этого учебника
Времена, когда ток обнаруживался с помощью личных ощущений ученых, пропускавших его через себя, давно миновали. Теперь для этого применяют специальные приборы, называемые амперметрами.
Амперметр — это прибор, служащий для измерения силы тока. Что понимают под силой тока?
Обратимся к рисунку 21, б. На нем выделено поперечное сечение проводника, через которое проходят заряженные частицы при наличии в проводнике электрического тока. В металлическом проводнике этими частицами являются свободные электроны. В процессе своего движения вдоль проводника электроны переносят некоторый заряд. Чем больше электронов и чем быстрее они движутся, тем больший заряд будет ими перенесен за одно и то же время.
Силой тока называется физическая величина, показывающая, какой заряд проходит через поперечное сечение проводника за 1 с.
Пусть, например, за время t = 2 с через поперечное сечение проводника носители тока переносят заряд q = 4 Кл. Заряд, переносимый ими за 1 с, будет в 2 раза меньше. Разделив 4 Кл на 2 с, получим 2 Кл/с. Это и есть сила тока. Обозначается она буквой I:
I — сила тока.
Итак, чтобы найти силу тока I, надо электрический заряд q, прошедший через поперечное сечение проводника за время t, разделить на это время:
I = q/t (10.1)
Единица силы тока называется ампером (А) в честь французского ученого А. М. Ампера (1775—1836). В основу определения этой единицы положено магнитное действие тока, и мы на нем останавливаться не будем.

Если сила тока I известна, то можно найти заряд q, проходящий через сечение проводника за время t. Для этого надо силу тока умножить на время:
q = It. (10.2)
Полученное выражение позволяет определить единицу электрического заряда — кулон (Кл):
1 Кл = 1 А · 1 с = 1 А·с.
1 Кл — это заряд, который проходит за 1 с через поперечное сечение проводника при силе тока 1 А.
Помимо ампера на практике часто применяются и другие (кратные и дольные) единицы силы тока, например миллиампер (мА) и микроампер (мкА):
1 мА = 0,001 А, 1 мкА = 0,000001 А.
Как уже говорилось, измеряют силу тока с помощью амперметров (а также милли- и микроамперметров). Демонстрационный гальванометр, о котором упоминалось выше, представляет собой обычный микроамперметр.
Существуют разные конструкции амперметров. Амперметр, предназначенный для демонстрационных опытов в школе, изображен на рисунке 28. На этом же рисунке приведено его условное обозначение (кружок с латинской буквой «А» внутри).
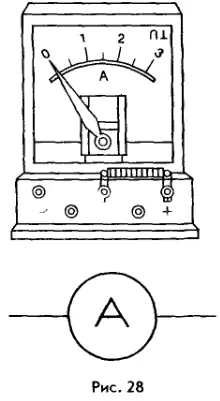
При включении в цепь амперметр, как и всякий другой измерительный прибор, не должен оказывать заметного влияния на измеряемую величину. Поэтому амперметр устроен так, что при его включении сила тока в цепи почти не изменяется.
В зависимости от назначения в технике используют амперметры с разной ценой деления. По шкале амперметра видно, на какую наибольшую силу тока он рассчитан. Включать его в цепь с большей силой тока нельзя, так как прибор может испортиться.
Для включения амперметра в цепь ее размыкают и свободные концы проводов присоединяют к клеммам (зажимам) прибора. При этом необходимо соблюдать следующие правила:
1) амперметр включают последовательно с тем элементом цепи, в котором измеряют силу тока;
2) клемму амперметра со знаком «+» следует соединять с тем проводом, который идет от положительного полюса источника тока, а клемму со знаком «–» — с тем проводом, который идет от отрицательного полюса источника тока.
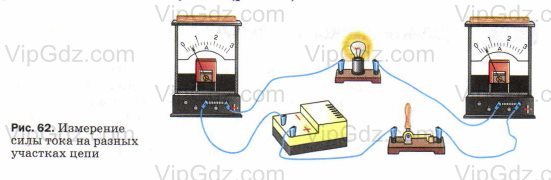
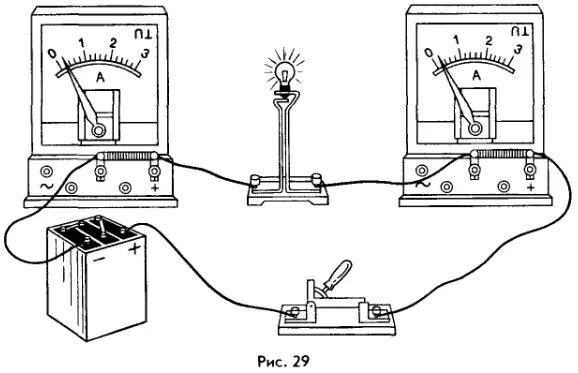
При включении амперметра в цепь не имеет значения, с какой стороны (слева или справа) от исследуемого элемента его подключать. В этом можно убедиться на опыте (рис. 29). Как видим, при измерении силы тока, проходящего через лампу, оба амперметра (и тот, что слева, и тот, что справа) показывают одно и то же значение.
??? 1. Что такое сила тока? Какой буквой она обозначается? 2. По какой формуле находится сила тока? 3. Как называется единица силы тока? Как она обозначается? 4. Как называется прибор для измерения силы тока? Как он обозначается на схемах? 5. Какими правилами следует руководствоваться при включении амперметра в цепь? 6. По какой формуле находится электрический заряд, проходящий через поперечное сечение проводника, если известны сила тока и время его прохождения?
- Подробности
- Обновлено 19.01.2019 23:28
- Просмотров: 419
Назад в «Оглавление»

О чем умолчал Перышкин?
О том, как сделать домашнее задание, ответить на вопросы и решить задачи в упражнениях!
Уверена, что думающие ученики сначала всё сделают сами, а эти сведения будут помощью «застрявшим в пути».
Ответы на ДЗ по физике помогут вам проверить себя и найти ошибки.
Ответы на ДЗ из упражнений соответствуют всем выпускам учебников этого автора, начиная с 1989 г.
Так как номера упражнений с одинаковыми вопросами в разных выпусках различаются, ответы на вопросы к упражнениям скомпонованы по темам параграфов.
На этой странице ГДЗ по темам: «Сила тока. Единицы силы тока. Амперметр. Измерение силы тока»



Дерзайте!
Сила тока
1. Выразите в амперах силу тока, равную 2000 мА; 100 мА; 55 мА; 3 кА.
2000 мА = 2А
100 мА = 0,1 А
55 мА = 0,055 А
3 кА = 3000 А
2. Сила тока в цепи электрической плитки равна 1,4 А.
Какой электрический заряд проходит через поперечное сечение её спирали за 10 мин?

3. Сила тока в цепи электрической лампы равна 0,3 А.
Сколько электронов проходит через поперечное сечение спирали за 5 мин?

Амперметр. Измерение силы тока
1. При включении в цепь амперметра так, как показано на рисунке 63, а, сила тока была 0,5 А.
Каковы будут показания амперметра при включении его в ту же цепь так, как изображено на рисунке 63, б?
При переставлении местами в цепи лампы и амперметра сила тока не изменится, т.к. при последовательном включении приборов сила тока в цепи везде одинакова.
2. Как можно проверить правильность показаний амперметра с помощью другого амперметра, точность показаний которого проверена?
Надо подключить оба амперметра последовательно в электрическую цепь, где измеряется сила тока.
При последовательном подключении в цепь проверяемого и точного амперметров их показания должны быть одинаковы.
Если показания проверяемого амперметра отличаются от показаний точного, то проверяемый амперметр неисправен.
3. Рассмотрите амперметры, данные на рисунках 61, 62.
Определите цену деления шкалы каждого амперметра.
Какую наибольшую силу тока они могут измерять? Перерисуйте шкалу амперметра (см. рис. 61, а) в тетрадь и покажите, каково будет положение стрелки при силе тока 0,3 А и 1,5 А.

Для вып. 1989 г. (1 и 2):
Ц.Д. = (2А – 1А) : 5 = 0,2А и Iмакс = 3А
Ц.Д = (2А – 1А) : 10 = 0,1А и Iмакс = 2А
Для вып. 2010г. – синий и 2013г – белый (1 и 3):
Ц.Д. = (2А – 1А) : 5 = 0,2А и Iмакс = 3А
Ц.Д. = (2А – 1,5А) : 10 = 0,05А и Iмакс = 2А
4.
Имеется точный амперметр. Как, пользуясь им, нанести шкалу на другой, ещё не проградуированный амперметр?
Подключить оба амперметра последовательно в электрическую цепь.
Их показания должны всегда совпадать.
Пропускать токи разной величины, при этом отмечать положение стрелки на шкале градуируемого амперметра и подписывать величину тока, как на точном амперметре.
Назад в «Оглавление»
Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:
– выставить на тестере максимально допустимый диапазон,
– присоединить щупы прибора к месту разрыва цепи.
Применив закон Ома, искомую величину можно также определить расчетным путем:
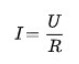
где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).
В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.
Типы соединений резисторов
Соединение элементов в одну цепь осуществляется следующими способами:
-
последовательно;
-
параллельно;
-
смешанно.
Общие схемы типов соединений представлены на рисунке 1.
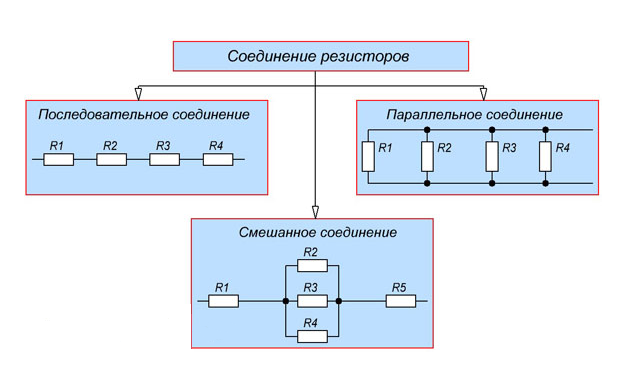
Рисунок 1. Типы соединений резисторов
Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)
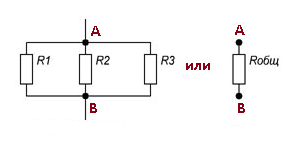
Рисунок 2. Параллельное соединение резисторов
Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.
При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.
Как найти сопротивление параллельно соединенных резисторов?
Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:
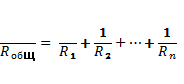
и рассчитывается по формуле:
![]()
Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R1= R2=7Ом (см. рис.3а)
R12= 7*7/ (7+7) = 3,5Ом
Сопротивление на участке АВ
(1– 2) в 2 раза меньше R каждого из резисторов.
При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R3=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R12= 3,5Ом
Rобщ= 3,5*7/ (3,5+7) = 2,33 Ом
R123< R3
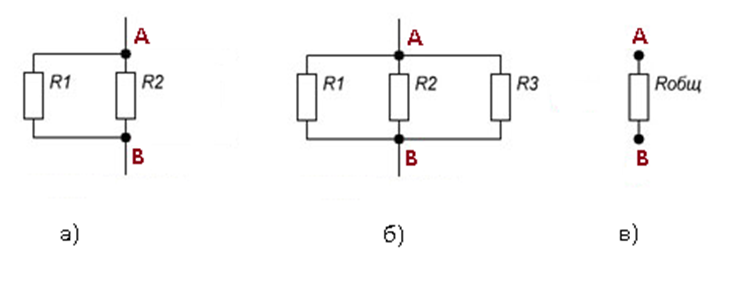
Рисунок 3. Увеличение цепи параллельного соединения резисторов
Из расчетов следует, что общее сопротивление (см. рис.3в) всегда будет меньше сопротивления любого параллельно включенного резистора. Такое условие обеспечивается равенством токов на входе и выходе узлов или групп параллельных резисторов и постоянством напряжения в сети.
Что такое последовательное соединение резисторов?
При последовательном соединении резисторы подсоединяются друг за другом, при этом конец предыдущего резистора соединен с началом последующего резистора (рисунок 4).
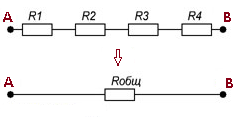
Рисунок 3. Последовательное соединение резисторов.
Потоку заряженных частиц при прохождении участка АВ предоставлен один путь, поэтому, чем больше резисторов подсоединено, тем большее сопротивление движущимся заряженным частицам они оказывают, то есть общее сопротивление участка цепи Rобщ возрастает.
Формула для расчета общего сопротивления при последовательном соединении имеет вид:
Как рассчитать напряжения на последовательно соединенных резисторах?
Последовательное соединение резисторов увеличивает общее сопротивление. Ток во всех частях схемы будет одинаковым, при этом будет определяться падение напряжения на каждом резисторе.
Общее напряжение питания на резисторах, соединенных последовательно, равно сумме разностей потенциалов на каждом резисторе:
URобщ =UR1+ UR2 + UR3+ UR4
Применив закон Ома, можно вычислить напряжение на каждом резисторе:
UR1=I*R1, UR2=I*R2, UR3=I*R3, UR4=I*R4
Напряжение на участке АВ рассчитывается по формуле:
UАВ=I* (R1
+ R2+R3+R4)
А ток в цепи:
![]()
Резисторы, соединенные последовательно, применяются в электротехнике в качестве делителя напряжения.
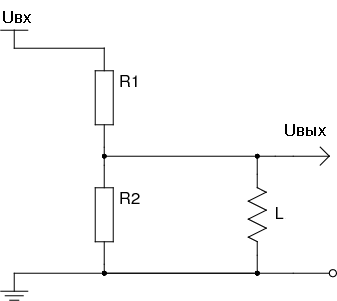
Рисунок 5. Схема простейшего делителя напряжения
Регулируя сопротивление обоих резисторов можно выделить требуемую часть входящего напряжения. При необходимости деления напряжения на несколько частей к источнику напряжения подключается несколько последовательно соединенных резисторов.
Смешанное соединение резисторов
В электротехнике наиболее распространено использование различных комбинаций параллельного и последовательного подключения. Силу тока при смешанном соединении резисторов определяют путем разделения цепи на последовательно соединенные части. Однако для определения общего сопротивления в случае параллельного сопротивления различных частей следует применять соответствующую формулу.
Алгоритм расчета смешанного подключения аналогичен правилу расчета базовой схемы последовательного и параллельного подключения резисторов. В этом нет ничего нового: нужно правильно разложить предложенное решение на пригодные для расчета части. Участки с элементами подключаются поочередно или параллельно. Гибридное резистивное соединение представляет собой комбинацию последовательного и параллельного. Эту комбинацию иногда называют последовательно-параллельным соединением.
На рисунке 6 представлена схема смешанного соединения резисторов.
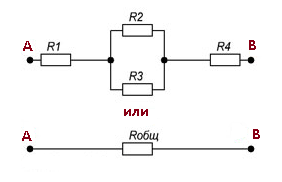
Рисунок 6. Смешанное соединение резисторов.
На рисунке показано, что резисторы R2 и R3
соединены параллельно, а R1, R23
и R4 последовательно.
Чтобы рассчитать сопротивление этого соединения, вся схема делится на простейшие части, начиная с параллельного или последовательного сопротивления. Тогда следующий алгоритм выглядит следующим образом:
1. Определите эквивалентное сопротивление части резистора, подключенной параллельно.
2. Если эти части содержат резисторы, включенные последовательно, сначала рассчитайте их сопротивление.
3. Вычислив эквивалентное сопротивление резистора, перерисовываем схему. Обычно схема получается из последовательного эквивалентного сопротивления.
4. Рассчитайте сопротивление цепи.
Другие способы подключения хорошо видны на примере, показанном на рисунке. Без специальных расчетов очевидно, что параллельное соединение резисторов создает несколько путей для тока. Следовательно, в одиночном контуре его сила будет меньше по сравнению с контрольными точками на входе и выходе. При этом напряжение на отметке остается неизменным.
Пример участка цепи для расчета сопротивления смешанного соединения показан на рисунке 5.
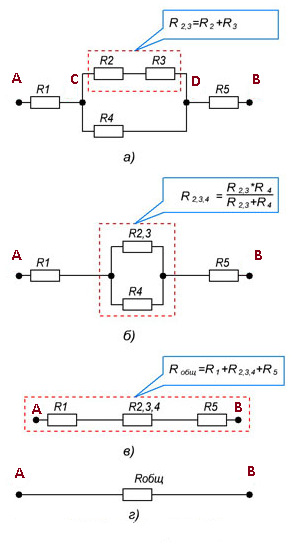
Рисунок 7. Общее сопротивление участка цепи со смешанным соединением резисторов.
Расчет электрических параметров необходим для правильных построений цепей. Поскольку целью использования электричества в электротехнике является задача по выполнению током работы, то встает вопрос о том, как найти силу тока. Данный параметр используют при вычислениях мощности и в расчетах потребления электрической энергии.
Существуют разные способы определения этого важного параметра, которые мы рассмотрим в данной статье.
Формулами
Параметры электрического тока всегда взаимосвязаны. Например, изменение величины нагрузки отображается на показателях других величин. Причем эти изменения подчиняются соответствующим законам, которые выражаются через формулы. Поэтому на практике для нахождения силы тока часто используют соответствующие формулы.
Через заряд и время
Вспомним определение (рис.1): электричество – это величина заряда, движимого силами электрического поля, преодолевающего за единицу времени условную плоскость проводника, называемую поперечным сечением проводника.

Таким образом, если известен электрический заряд, прошедший через проводник за определенное время, то не трудно найти величину этого заряда прошедшего за единицу времени, то есть: I = q/t
Через мощность и напряжение
В паспорте электроприбора обычно указывается его номинальная мощность и параметры электрической сети, для работы с которой он предназначен. Имея в распоряжении эти данные, можно вычислить силу тока по формуле: I = P/U.
Данное выражение вытекает из формулы для расчета мощности: P = IU.
Через напряжение или мощность и сопротивление
Силу электричества на участке цепи определяют по закону Ома. Для этого необходимо знать следующие параметры: сопротивление и напряжение на этом участке. Тогда I = U/R. Если известна мощность нагрузки, то ее можно выразить через квадрат силы тока умноженной на сопротивление участка: P = I2R, откуда
![]()
Для полной цепи эту величину вычисляют по закону Ома, но с учетом параметров источника питания.
Через ЭДС, внутреннее сопротивление и нагрузку R
Применяя закон Ома, адаптированный для полной цепи, вы можете вычислить максимальный ток по формуле I = ε / (R+r′), если известны параметры:
- внешнее сопротивление проводников (R);
- ЭДС источника питания (ε);
- внутреннее сопротивление источника, обладающего ЭДС (r′).
Примечание! Реальные источники питания обладают внутренним сопротивлением. Поскольку в электрической цепи
показатель силы тока может уменьшаться в связи с возрастанием сопротивления источника питания или в результате падения ЭДС. Именно из-за роста внутреннего сопротивления садится аккумулятор и ослабевает ЭДС элементов питания.
Закон Джоуля-Ленца
Казалось бы, что расчет силы тока по количеству тепла, выделяющегося в результате нагревания проводника, не имеет практического применения. Однако это не так. Рассмотрим это на примере.
Пусть требуется найти силу тока во время работы электрочайника. Для этого доведите до кипения 1 кг воды и засеките время в секундах. Предположим, начальная температура составляла 10 ºС. Тогда Q = Cm(τ – τ0) = 4200 Дж/кг× 1 кг (100 – 10) = 378 000 Дж.

Из закона Джоуля-Ленца (изображение на рис. 2) вытекает формула:

Измерив сопротивление электроприбора и подставив значения в формулу, получим величину потребляемого тока.
Измерительными приборами
Если под руками имеются измерительные приборы, то с их помощью довольно просто найти силу тока. Необходимо лишь соблюдать правила измерений и не забывать о правилах безопасности.
Амперметром
Пользуясь приборами для измерения ампеража, следует помнить, что они подключаются в цепи последовательно. Внутреннее сопротивление амперметра очень маленькое, поэтому прибор легко выводится из строя, если проводить измерения пределами значений, для которых он рассчитан.
Схема подключения амперметра показана на рисунке 3. Обратите внимание на то, что на участке измеряемой электрической цепи обязательно должна быть нагрузка.

Большинство аналоговых амперметров, например, таких, как на рисунке 4, предназначены для измерений параметров в цепях с постоянными токами.

Обратите внимание распределение шкалы амперметра. Цена первого деления 50 А, а всех последующих – 10 А. Максимальная величина, которую можно измерить данным амперметром не должна превышать 300 А. Для измерений электрической величины в меньших либо в больших пределах следует применять соответствующие приборы, предназначенные для таких диапазонов. В этом смысле универсальность амперметра ограничена.
При измерениях постоянных токов необходимо соблюдать полярность щупов при подключении амперметра. Для подключения прибора требуется разрывать цепь. Это не всегда удобно. Иногда вычисление силы тока по формуле является предпочтительней, особенно если приходится проводить измерения в сложных электротехнических схемах.
Мультиметром
Преимущество мультиметра в том, что этот прибор многофункциональный. Современные мультиметры цифровые. У них есть режимы для измерений в цепях постоянных и переменных токов. В режиме измерения силы тока этот измерительный прибор подключается в цепь аналогично амперметру.
Перед включением мультиметра в цепь, всегда проверяйте режим измерений, а пределы измерения выбирайте заведомо большие предполагаемой силы тока. После первого измерения можно перейти в режим с меньшим диапазоном.
Для работы с переменным напряжением переводите прибор в соответствующий режим. Считывайте значения с дисплея после того, как цифры перестанут мелькать.
Примеры
Покажем на простых примерах, как решать задачи на вычисление силы тока по формуле.
Задача 1.
На участке цепи имеются три параллельно включенных резистора (см. рис. 5). Значения сопротивлений резисторов: R1 = 5 Ом; R2 = 25 Ом; R3 = 50 Ом. Требуется рассчитать силу тока для каждого резистора и на всём участке, если на нем поддерживается постоянное напряжение 100 В.

Решение: При параллельном соединении нагрузочных элементов U = const, то есть, напряжение одинаково на всех резисторах и составляет 100 В. Тогда, по закону Ома I = U/R
- I1 = U/R1 =100/5 = 20 А;
- I2 = U/R2 =100/25 ≈ 4 А;
- I3 = U/R3 =100/50 = 2 А.
Для вычисления искомого параметра на всем участке цепи, нам необходимо знать общее сопротивление этого участка. Учитывая тот факт, что при параллельном соединении нагрузочных элементов в цепи их общее сопротивление равно:
![]()
Имеем: 1/R= 1/5 + 1/25 + 1/50 = 13/50; R = 50/13 ≈ 3.85 (Ом)
Тогда: I = U/R = 100 В/3,85 Ом ≈26 А.
Ответ:
- Сила тока на сопротивлениях: I1 =20 А; I2 = 4А; I3 = 2 А.
- Сила тока, поступающего на рассматриваемый участок цепи равна 26 А.
Задача 2.
Мощность электрочайника 2 кВт. Чайник работает от городской сети под напряжением 220 В. Сколько электричества потребляет этот электроприбор?
Решение:
Воспользуемся формулой для нахождения силы тока, включающей напряжение и мощность: I = P/U.
- 2 кВт преобразим в ватты: 2 кВт = 2000 Вт.
- Подставляем данные: I = 2 000 Вт/ 220 В ≈ 9 А
- Ответ: Нагревательный элемент электрочайника рассчитан на 9 А.
Задача 3.
Вычислить силу тока в цепи, если известно, что сопротивление составляет 5 Ом, ЭДС источника питания 6 В, а его внутреннее сопротивление составляет 1 Ом.
Решение.
Применяя закон Ома для полной цепи, запишем: I = ε / (R+r′)
I = 6 В / (5 Ом + 1 Ом) = 1 А.
Ответ: сила тока 1 А.
Задача 4.
Сколько энергии потребляет электроплита за 2 часа работы, если сопротивление нагревательного элемента 40 Ом?
Решение:
За время t электричество выполнит работу A = U*I*t.
Напряжение сети известно – оно составляет 220 В.Силу тока находим по формуле: I = U/R, тогда A = (U2/R)*t или
A = ((220 В)2 / 40 Ом) * 2 ч = 2420 Втч = 2,42 кВтч
Ответ: За 2 часа работы электроплита потребляет 2,42 кВт часов электроэнергии.
Применяя формулы для вычисления параметров электричества, пользуясь фундаментальными законами физики можно находить неизвестные данные для составных элементов цепей и электроприборов с целью оценки их состояния. В каждом отдельном случае необходимо определить известные параметры тока, которые можно использовать в дальнейших вычислениях. Обычно, это напряжение, мощность или сопротивление нагрузки.
Если можно обойтись без измерений амперметром – лучше прибегнуть к вычислениям, даже если при этом потребуется измерить напряжение. Такое измерение можно проводить без разрыва электрической цепи, чего нельзя сделать при помощи амперметра.
