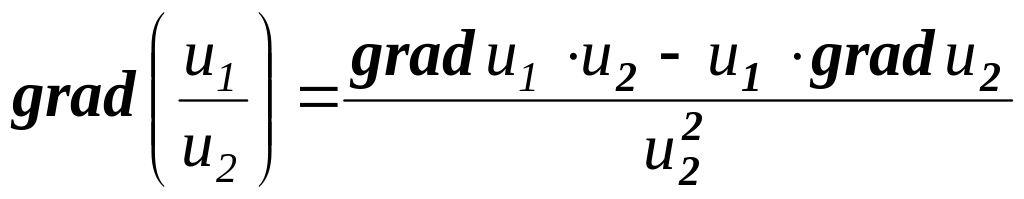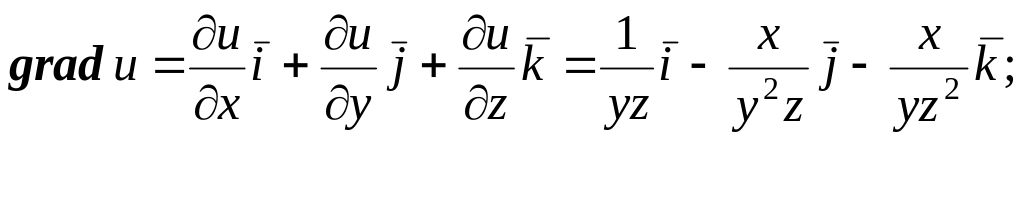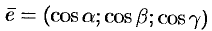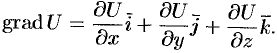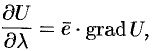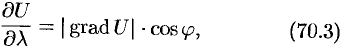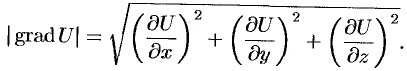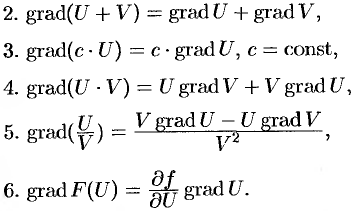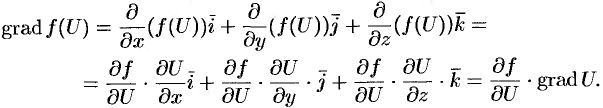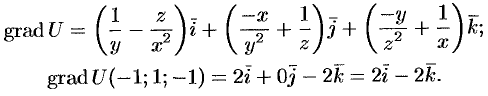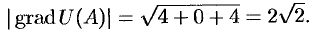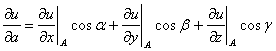Как найти наибольшую скорость возрастания функции

При изучении скалярных полей наряду с функций рассматривается некоторый вектор, тесно связанный с этой функцией, – градиент скалярного поля.

Градиентом в точке скалярного поля, заданного дифференцируемой функцией , называется вектор, равный

.

Таким образом, каждой точке скалярного поля, заданного дифференцируемой функцией , соответствует не только значение этой функции, но и вполне определенный вектор .

Между градиентом функции в данной точке и производной по направлению в той же точке имеется связь, которая устанавливается следующей теоремой.

Теорема. Проекция вектора На единичный вектор равна производной функции по направлению :

.

Доказательство. Пусть . Из векторной алгебры известно, что проекция какого-либо вектора на другой вектор равна скалярному произведению этих векторов.

Так как , , то

.

Учитывая, что производная по направлению выражает скорость изменения скалярного поля в этом направлении, можно сказать, что проекция на вектор равна скорости изменения поля в направлении вектора .

Обозначим через угол между единичным вектором и . Тогда .

Поэтому .

Если направления векторов и совпадают (), то производная по направлению имеет, очевидно, наибольшее значение, равное .

Таким образом, есть вектор, указывающий Направление наибольшего возрастания поля в данной точке и имеющий Модуль равный скорости этого возрастания.

Рассмотрим кривую , лежащую на поверхности уровня и проходящую через точку . Градиент функции в точке обладает следующими свойствами: перпендикулярен к вектору , направленному по касательной к кривой в точке .

В случае плоского скалярного поля, заданного дифференцируемой функцией двух переменных , градиент определяется формулой

.

Его связь с производной по направлению выражается равенством

,

Где – угол между единичным вектором и . Вектор перпендикулярен к касательной, проведенной к линии уровня в точке .

Пример 16. Найти наибольшую скорость возрастания функции

в точке .

Решение. Наибольшая скорость возрастания функции равна модулю градиента этой функции. Найдем градиент функции :

,

.

В точке имеем .

Тогда наибольшая скорость возрастания функции равна

.

Пример 17. Найти скорость изменения скалярного поля, определяемого функцией в точке в направлении касательной, проведенной к параболе в этой точке в сторону возрастания координаты , и наибольшую скорость изменения поля в этой точке.

Решение. Скорость изменения скалярного поля в заданном направлении есть производная скалярного поля по направлению вектора , задающего направление.

,

Где ; – направляющие косинусы вектора , . Вектор возьмем на касательной к параболе в , для чего составим уравнение касательной

,

,

– уравнение касательной.

На найденной касательной возьмем точку с любой координатой (), например . Тогда

.

Найдем значения производной по направлению в точке :

,

.

Тогда .

Наибольшая скорость изменения поля в точке есть .

Так как , то

.

Величина наибольшей скорости

.

< Предыдущая		Следующая >

Градиент скалярного поля

Градиент (от лат.
Gradiens − шагающий) − характеристика,
показывающая направление наискорейшего
возрастания некоторой величины, значение
которой меняется от одной точки
пространства к другой. Например, если
взять высоту поверхности Земли над
уровнем моря, то её градиент в каждой
точке поверхности будет показывать
направление «в гору».

Градиент является
векторной функцией, а величина, которую
он характеризует, − функцией скалярной.

Используется
понятие градиента различных физических
полей, например, градиент концентрации
− нарастание или уменьшение по какому-либо
направлению концентрации растворённого
вещества, градиент температуры −
увеличение или уменьшение по направлению
температуры среды и т.д.

Градиентом от
функции


в точке

называется вектор, обозначаемый


и определяемый формулой:

.

(6)

Так как компоненты
градиента являются частными производными,
нетрудно получить следующие свойства
градиента, которые вытекают из свойств
операции дифференцирования:

(7)

.

Связь
градиента и производной по направлению.

Физический
смысл градиента

Используя формулы
(4), (6), представим производную функции

в точке
по
направлению

в виде скалярного произведения градиента
функции на единичный вектор

:

(8)

.

Производная функции
по направлению равна проекции вектора
градиента функции на это направление.

Так как вектор


− единичный, и

,
используя определение скалярного
произведения формулу (8), преобразуем к
виду:

.
(9)

Здесь


− угол между векторами

и

.

Из последнего
равенства следует, что производная
функции по направлению имеет наибольшую
величину при

,
т.е. в направлении градиента функции.
Отсюда вытекает физический смысл
градиента функции. Величина максимальной
скорости возрастания функции в данной
точке равна

модулю градиента
и определяется формулой:

.
(10)

Пример 3. Найти
наибольшую скорость возрастания функции



в точке

.

Решение. Наибольшая
скорость возрастания функции есть
модуль ее градиента. По формуле (4) имеем:

Найдем значение
градиента функции в точке М:

Наибольшая скорость
возрастания функции равна

.

Геометрический
смысл градиента

Рассмотрим семейство
линий уровня плоского скалярного поля
(2).

Градиент функции
в точке перпендикулярен её линии уровня,
проходящей через эту точку, т.е. направлен
по нормали к линии уровня.

В самом деле,
дифференцируя равенство (2), получаем в
точках линии уровня

,
тогда из формулы (9) следует, что

.

Модуль градиента
показывает максимальную скорость
изменения функции в окрестности точки,
то есть частоту линий уровня. Например,
линии уровня высоты изображаются на
топографических картах, при этом модуль
градиента показывает крутизну спуска
или подъема в данной точке.

В случае
пространственного поля градиент функции
направлен по нормали к поверхности
уровня в сторону возрастания функции.

Оператор
Гамильтона

Дифференциальные
операции удобно представлять с помощью
оператора Гамильтона или оператора
«набла»:

.
(11)

Оператор


будем рассматривать как символический
вектор с координатами

,
а операции с ним проводить по правилам
векторной алгебры.

Если


− скалярная функция, то действие
оператора

на эту функцию дает ее градиент:

.

Векторное
поле

Если каждой точке

пространства
ставится в соответствие вектор

,
то говорят, что задано векторное поле.

Примерами векторных
полей могут служить поле скоростей
частиц движущейся жидкости, силовое
поле, поле электрической напряженности,
поле сил тяготения.

В декартовой
системе координат векторное поле можно
записать в виде:

.
(12)

Скалярные функции


однозначно
определяют векторное поле. Векторное
поле может быть плоским, в этом случае


.

Пример 4. Найти
векторное поле скоростей

точек
твердого тела, вращающегося с постоянной
угловой скоростью


вокруг оси Оz.

Решение. Скорость



точки

равна векторному произведению


− радиус-вектор точки

вращающегося тела относительно какой-либо
точки оси вращения. Примем эту неподвижную
точку за начало координат.

Тогда

Геометрической
характеристикой векторных полей являются
векторные линии (линии тока), позволяющие
наглядно представить векторные поля.

Векторные линии
− кривые, в каждой точке которых вектор

является
касательным вектором. Для конкретных
полей это понятие имеет ясный физический
смысл. Например, в поле скоростей текущей
жидкости векторными линиями будут
линии, по которым движутся частицы
жидкости (линии тока), для магнитного
поля векторными линиями будут силовые
линии, проходящие из северного полюса
в южный. Через каждую точку проходит
одна линия тока. В декартовых координатах
дифференциальные уравнения векторных
линий имеют вид:

.
(13)

Пример 5. Найти
векторные линии поля линейных скоростей
тела, вращающегося с постоянной скоростью

вокруг оси Оz.

Данное поле
определено вектором


(см. предыдущий пример). По формуле (13)
имеем:

,
отсюда

Интегрируя, получим:

Векторными линиями
поля скоростей точек тела, вращающегося
с постоянной угловой скоростью вокруг
оси Oz, являются
окружности с центрами на этой оси. Они
лежат в плоскостях, перпендикулярных
к оси вращения.

Поток
векторного поля

Пусть задано
векторное поле формулой (12). Для наглядности
будем считать его полем скоростей потока
жидкости. Рассмотрим ориентированную
поверхность S с нормалью


,
находящуюся в потоке и пропускающую
жидкость. Выясним, какое количество
жидкости протекает через поверхность
S.

Разобьем поверхность
S на элементарные
площадки

,
выберем на каждой точку


− нормаль к площадке в этой точке. Будем
приближенно считать каждую площадку
плоской, а вектор


− постоянным по модулю и одинаково
направленным в каждой точке площадки.
Общее количество жидкости, протекающее
через всю поверхность S
за единицу времени, найдем, вычислив
сумму

.

Точное значение
получим предельным переходом суммы при
неограниченном увеличении числа
элементарных площадок и стремлении к
нулю их диаметров:

.

Независимо от
физического смысла вектора

полученный
интеграл называется потоком векторного
поля.

Потоком векторного
поля

через
ориентированную поверхность S
называется поверхностный интеграл 1-го
рода по площади поверхности:

.
(14)

Выражая скалярное
произведение через координаты векторов,
получаем другую форму записи:

.
(15)

Используя связь
поверхностных интегралов первого и
второго рода, поток векторного поля
можно записать в координатной форме:

.
(16)

Отметим, что поток
векторного поля есть величина скалярная.
Его величина равна объему жидкости,
которая протекает через поверхность
за единицу времени. В этом состоит
физический смысл потока поля.

Рис. 2

Особый интерес
вызывает случай замкнутой поверхности
S, ограничивающей
объем V. В этом случае
внешнюю нормаль к поверхности S
берут за положительное направление
нормали и говорят о потоке изнутри
поверхности. Величина потока дает
разность между количеством жидкости,
вытекающей из области V
и втекающей в нее за единицу времени.
При этом, если значение потока положительно,


,
то из области V вытекает
больше жидкости, чем в нее втекает, т.
е. внутри области имеются дополнительные
источники. Если значение потока
отрицательно,

,
то внутри области V
имеются стоки, поглощающее жидкость.
При


в области отсутствуют источники, либо
они компенсированы стоками.

Пример 6. Найти
поток радиус-вектора


через внешнюю сторону поверхности
прямого конуса с вершиной в начале
координат. Высота конуса Н , радиус
основания конуса R.

Решение. В
соответствии с формулой (14) найдем
поток:

Поток радиус-вектора
точек боковой поверхности конуса равен
нулю, так как


и подынтегральная функция обращается
в ноль:

.

Вычислим поток
поля через основание

конуса. Подынтегральная
функция в этом случае есть проекция
радиус-вектора на нормаль, т. е. высота
конуса:

Окончательно
получим:

Дивергенция
векторного поля

Важной характеристикой
векторного поля является дивергенция
(или расходимость), характеризующая
распределение и интенсивность источников
и стоков поля.

Дивергенцией
векторного поля


в точке М называется скалярная
величина:

.
(17)

(Обратите внимание,
насколько компактнее запись с помощью
оператора набла

).

Используя понятия
потока и дивергенции векторного поля,
запишем известную в математическом
анализе формулу Остроградского-Гаусса:

. (18)

Рассматривая
трехмерную область V ,
ограниченную замкнутой поверхностью
S, в векторном поле

,
можно утверждать, что левая часть формулы
(18) представляет собой поток вектора
через поверхность S,
а правая − его дивергенцию.
Поэтому формулу (18) запишем в векторном
виде:

.
(19)

Формула
Остроградского-Гаусса означает, что
поток векторного поля через замкнутую
поверхность в направлении внешней
нормали равен интегралу от дивергенции
поля по объему, ограниченному этой
поверхностью.

Используя формулу
(19) и теорему о среднем, несложно показать,
что в каждой точке М выполняется
равенство:

.
(20)

На основании
формулы (20) можно дать другое определение
дивергенции, эквивалентное данному
ранее.

Дивергенция
векторного поля в точке М является
пределом отношения потока вектора через
поверхность, окружающую точку М, к
объему области, ограниченной этой
поверхностью.

Так как поток и
объем не зависят от выбора системы
координат, то и дивергенция также не
зависит от выбора системы координат.

Выясним с помощью
формулы (20) физический смысл дивергенции.

Исходя из физического
смысла потока, можно сказать, что при


точка М представляет собой источник,
а при


точка М представляет собой сток.
Таким образом, дивергенция характеризует
мощность или плотность источника или
стока в точке. Если в объеме, ограниченном
замкнутой поверхностью, нет источников
и стоков, то

.

Векторное поле, в
каждой точке которого дивергенция поля
равна нулю
,
называется соленоидальным или трубчатым.

Пример 7. Найти
дивергенцию поля линейных скоростей
твердого тела, вращающегося с постоянной
скоростью

вокруг оси Оz.

Решение. Данное
поле определено вектором

(см. пример 4). По формуле (17) имеем:

Данное поле является
соленоидальным или трубчатым.

Циркуляция
векторного поля

Пусть в декартовой
системе координат в некоторой области
задано векторное поле:

,

кривая L
− кусочно-гладкая, расположенная
в этой области.

Пусть


− радиус-вектор точки М на контуре
L .

Известно, что
вектор



направлен по касательной к кривой в
направлении ее обхода, причем

,
где


‑ дифференциал дуги кривой,

.

Циркуляцией
векторного поля

вдоль кривой L называется
криволинейный интеграл от скалярного
произведения векторов


:

.
(21)

В силовом поле
циркуляция имеет простой физический
смысл, она выражает работу силового
поля при перемещении материальной точки
вдоль пути L.

Пример 8. Найти
циркуляцию вектора поля линейных
скоростей вращающегося тела вдоль
замкнутой кривой L,
лежащей в плоскости, перпендикулярной
оси вращения.

Решение. Данное
поле определено вектором

(см. пример 4). По формуле (21) имеем:

,

где

− площадь поверхности, ограниченной
кривой L.

Ротор
векторного поля. Формула Стокса

Ротором векторного
поля

называется
вектор

,
определяемый равенством:

.
(22)

Формула (22) может
быть переписана в другом виде:

.
(23)

Определение ротора
векторного поля с помощью оператора
«набла» записывается более компактно:

.

Ротор векторного
поля не зависит от выбора системы
координат.

С помощью понятий
циркуляции и ротора запишем формулу
Стокса:

Более компактно
эта формула запишется в векторной форме,
а также с использованием оператора
«набла»:

;

Таким образом,
циркуляция векторного поля

вдоль замкнутого контура L
равна потоку ротора этого векторного
поля через поверхность S
, ограниченную контуром L.

Пример 9.
Вычислить ротор поля скоростей твердого
тела,. вращающегося с постоянной скоростью

вокруг оси Оz.

Данное поле
определено вектором

(см. пример 4). Используя определение
ротора, получаем:

Ротор данного
векторного поля направлен по оси
вращения, его модуль равен удвоенной
угловой скорости.

Соленоидальное
поле

Соленоидальным
или трубчатым называется векторное
поле, в каждой точке которого дивергенция
поля равна нулю

.

Примерами
соленоидальных полей являются поле
линейных скоростей вращающегося твердого
тела (см. пример 4), магнитное поле,
создаваемое прямолинейным проводником,
вдоль которого течет электрический
ток.

Приведем некоторые
свойства соленоидальных полей.

• В соленоидальном
  поле поток вектора через любую замкнутую
  поверхность равен нулю. Это свойство
  вытекает из формулы Гаусса-Остроградского.
  Поэтому соленоидальное поле не имеет
  источников и стоков.

• Соленоидальное
  поле является полем ротора некоторого
  векторного поля. Если
  
  ,
  то существует такое поле
  
  ,
  что
  
  .
  Вектор

  
  называется векторным потенциалом поля
  
  
  .

• В соленоидальном
  поле поток вектора через поперечное
  сечение векторной трубки сохраняет
  постоянное значение.

Соседние файлы в папке Работы

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Градиент скалярного поля и его свойства

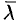
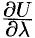
В каком направлении производная имеет наибольшее значение? Это направление указывает вектор, называемый градиентом скалярного ноля.

Можно заметить, что правая часть равенства (70.2) представляет собой скалярное произведение единичного вектора

и некоторого вектора .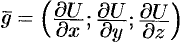

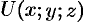
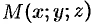
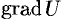
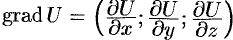
Вектор, координатами которого являются значения частных производных функции в точке , называют градиентом функции и обозначают , т. е. или

Отметим, что 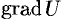есть векторная величина. Говорят: скалярное поле порождает векторное поле градиента . Теперь равенство (70.2) можно записать в виде

или

где — угол между вектором и направлением (см. рис. 269).

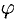
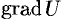
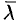
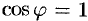
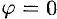
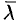
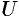
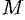
Из формулы (70.3) сразу следует, что производная но направлению достигает наибольшего значения, когда , т. е. при . Таким образом, направление градиента совпадает с направлением , вдоль которого функция (поле) меняется быстрее всего, т. е. градиент функции указывает направление наибыстрейшего возрастания функции. Наибольшая скорость изменения функции в точке равна

В этом состоит физический смысл градиента. На указанном свойстве градиента основано его широкое применение в математике и других дисциплинах.

Приведем важные свойства градиента функции.

Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.

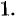
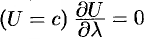
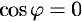
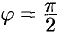
Действительно, по любому направлению вдоль поверхности уровня . Но тогда из (70.3) следует, что , т. е. .

Доказываются эти свойства на основании определения градиента. Докажем, например, последнее свойство. Имеем:

Замечание. Приведенные свойства градиента функции остаются справедливыми и для плоского поля.

Пример №70.2.

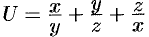
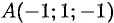
Найти наибольшую скорость возрастания функции в точке .

Решение:

Имеем:

Наибольшая скорость возрастания функции равна

Отметим, что функция будет убывать с наибольшей скоростью , если точка движется в направлении — (антиградиентное направление).

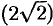
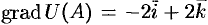
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Макеты страниц

Градиент функции

Градиент — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины u. Другими словами, направление градиента есть направление наибыстрейшего возрастания функции.

Назначение сервиса. Онлайн калькулятор используется для нахождения градиента функции нескольких переменных. (см. пример) При этом решаются следующие задачи:

• нахождение частных производных функции, запись формулы градиента, вычисление наибольшой скорости возрастания функции в указанной точке;
• вычисление градиента в точке A, нахождение производной в точке A по направлению вектора a;
• нахождение полного дифференциала функции.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Решение со всеми исходными формулами сохраняется в формате Word.

Полный дифференциал для функции двух переменных: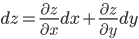

Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz

Алгоритм нахождения градиента

1. Вычисление частных производных по формуле:

   

2. Вычисление частных производных в точке A.
3. Нахождение направляющих углов вектора a.
4. Вычисление производной в точке A по направлению вектора a по формуле;

   

5. Наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).