Конечно, можно прикинуть на глазок и при некоторых способностях решить задачку в уме. Но давайте попытаемся предложить такое объяснение, которое будет понятно абсолютно всем. И для этого первым делом нам потребуется выяснить, что подразумевается под определением “средняя линия треугольника”. Для этого я предлагаю сначала изобразить сам прямоугольный треугольник со сторонами 6 и 8.

То, что мы его расположили на листочке в клеточку, позволяет легко и незамедлительно поставить риски на серединах сторон. Ведь именно это нам нужно для того, чтобы найти средние линии геометрической фигуры. Соединив полученные точки, мы увидим треугольник с теми же пропорциями, но существенно меньшими размерами. С длинами его сторон нам и предстоит разобраться.

Картинка наглядно демонстрирует следующее:
- Если AB = 8, то XZ = 4
- Если AC = 6, то YZ = 3
- Отрезок XY является гипотенузой прямоугольного треугольника со сторонами XZ и YZ.
Даже невооружённому глазу видно, что длина XY будет больше, чем любая из XZ и YZ. Ведь гипотенуза не может быть меньше катетов прямоугольного треугольника. Но нас интересует точное значение её длины. Для этого используем классический вариант – извлечём квадратный корень из суммы квадратов катетов красного треугольника.
- XY = Корень(XZ² + YZ²) = Корень(4² + 3²) = Корень(16 + 9) = Корень(25) = 5
Думаю, в том, что 5 больше 3-х и 4-х, ни у кого нет сомнений? Тогда можно дать однозначный ответ – наибольшей средней линией искомого треугольника является сторона XY, которая равна 5-ти.
P.S. Если кто-то не в курсе, то такая треугольная фигура со сторонами 3*4*5 издавна носит название “Египетский треугольник”. И опытные математики видят её издалека. Соответственно, они могут ответить на поставленный вопрос, не прибегая к банальным вычислениям. Но на то они и математики. 🙂
Задания
Версия для печати и копирования в MS Word
Тип 12 № 506338 

i
Катеты прямоугольного треугольника равны 6 и 8. Найдите наибольшую среднюю линию треугольника.
Спрятать решение
Решение.
Средняя линия в треугольнике равно половине стороны, которой она параллельна. Следовательно, наибольшая средняя линия параллельна гипотенузе и равна её половине. Длина гипотенузы равна: Значит, наибольшая средняя линия треугольник равна 5.
Ответ: 5.
Источники:
Апробация базового ЕГЭ по математике, 13—17 октября: вариант 120912;
Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166214.
Раздел кодификатора ФИПИ: Треугольники и их элементы
Спрятать решение
·
Помощь
Катеты прямоугольного треугольника равны 16 и 30. Найдите наибольшую среднюю линию треугольника.

Решение
Средняя линия прямоугольного треугольника, соединяющая середину двух сторон (в нашем случае катетов), параллельна третьей стороне (в нашем случае гипотенузе) и равна его половине.
Найдем длину гипотенузы по формуле Пифагора (пусть (a) и (b) – катеты прямоугольного треугольника, а (c) – гипотенуза):
(c^2=a^2+b^2;)
(c^2=16^2+30^2;)
(c=34).
По определению наибольшая средняя линия делит гипотенузу пополам. Значит, она равна (34div2=17).
Ответ: (17).
Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 23) (Купить книгу)
Катеты прямоугольного треугольника равны 16 и 30. Найдите наибольшую среднюю линию треугольника.
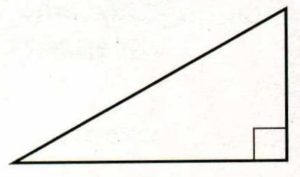
Решение:
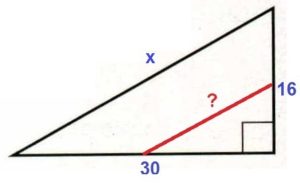
Наибольшая средняя линия треугольника будет, параллельна большей стороне, т.е. гипотенузе, найдём её:
х2 = 162 + 302
х2 = 256 + 900 = 1156
х = √1156 = 34
Средняя линия равна половине параллельного ей основания:
34/2 = 17
Ответ: 17.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.2 / 5. Количество оценок: 5
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Решение №1019 Катеты прямоугольного треугольника равны 16 и 30.
Катеты прямоугольного треугольника равны 16 и 30. Найдите наибольшую среднюю линию треугольника.


Наибольшая средняя линия треугольника будет, параллельна большей стороне, т.е. гипотенузе, найдём её:
х 2 = 16 2 + 30 2
х 2 = 256 + 900 = 1156
х = √1156 = 34
Средняя линия равна половине параллельного ей основания:
34/2 = 17
Ответ: 17.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Средняя линия треугольника – свойства, признаки и формулы
Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.
Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.
Определение и признаки средней линии треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
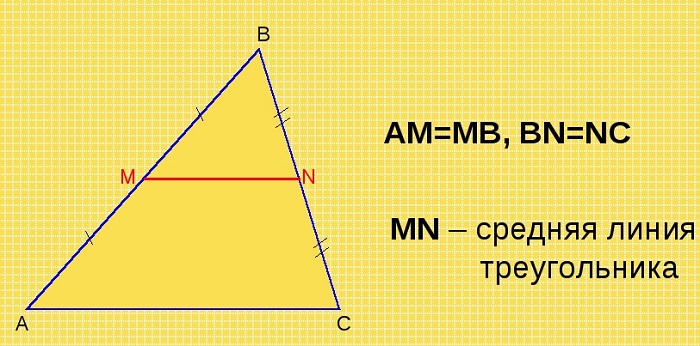
Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.
Доказательство следует из теоремы Фалеса.

Теорема о средней линии треугольника
Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.
Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.
По определению, MN – средняя линия ΔABC.
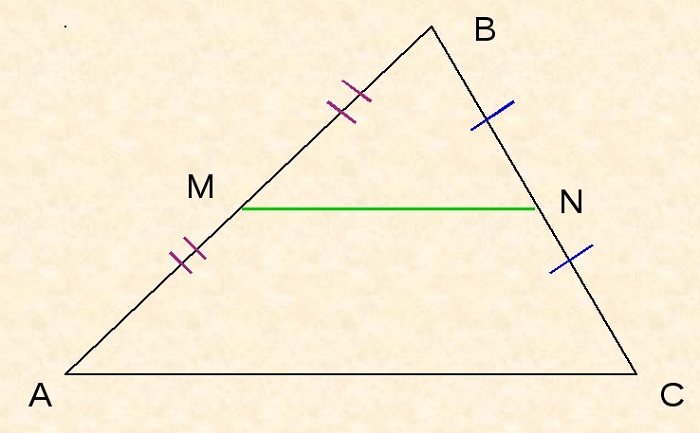
Необходимо доказать, что MN II AC, MN = ½AC.
Доказательства
Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.
Следовательно, MN II AC.
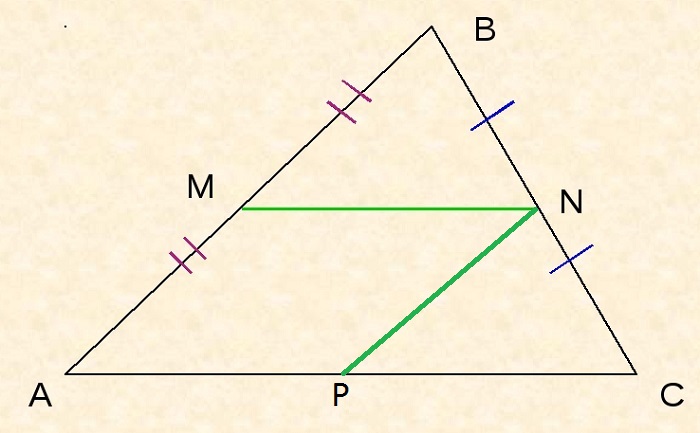
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.
Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.
Рассматриваются треугольники MBN и ABC. В них угол B является общим,
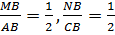
По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.
Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.
Формула MN = ½AC следует из условий
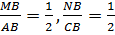
поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.
Рассматривается сумма векторов
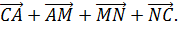
Поскольку в результате образуется замкнутая ломаная, то
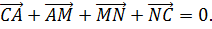
Отсюда следует, что
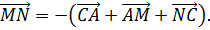
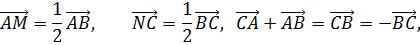
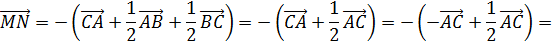
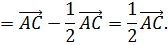
Из последнего равенства следуют условия теоремы.
Следствия из теоремы с доказательствами
Следствие №1
Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.

По определению стороны AB и BC делятся пополам, поэтому
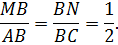
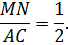
Из третьего признака подобия вытекает рассматриваемое свойство.
Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как
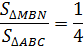
Следствие №2
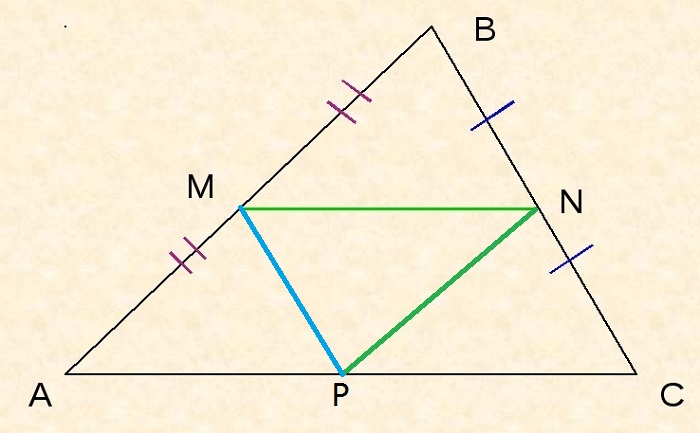
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.
Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.
Таким образом: ∠BNM = ∠BCA = ∠MPA.
Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.
Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.
Равенство остальных пар треугольников доказывается аналогично.
По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Свойства средней линии треугольника
Теорема и следствия из неё составляют основные свойства средней линии треугольника.
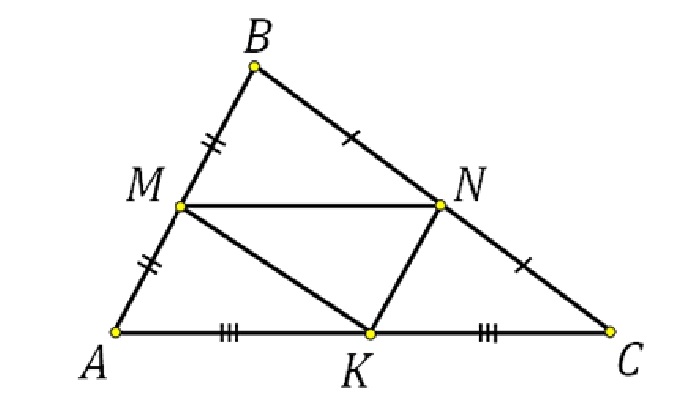
Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.
Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.
Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.
Средняя линия прямоугольного треугольника
Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.
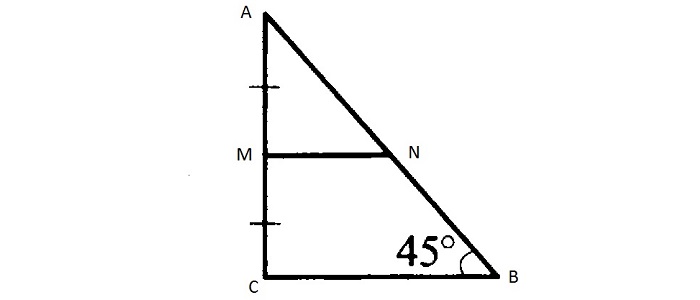
Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.
Пример решения задачи
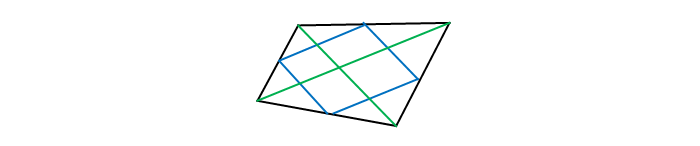
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.
Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.
Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.
Что такое средняя линия треугольника
В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.
Определение средней линии треугольника
Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.

- KL – средняя линия треугольника ABC
- K – середина стороны AB: AK = KB
- L – середина стороны BC: BL = LC
Свойства средней линии треугольника
Свойство 1
Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.
На рисунке выше:
Свойство 2
Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.
На рисунке выше:
- △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
- Стороны △KBL в два раза меньше соответствующих сторон △ABC:
AB = 2KB, BC = 2BL, AC = 2KL. - S△ABC = 4 ⋅ S△KBL
Свойство 3
В любом треугольнике можно провести три средние линии.

KL, KM и ML – средние линии треугольника ABC.
Свойство 4
Три средние линии треугольника делят его на 4 равных по площади треугольника.

Признак средней линии треугольника
Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.
Пример задачи
Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.
Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.

Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
BC = 10.
Таким образом, средняя линия LM = 1 /2 ⋅ BC = 1 /2 ⋅ 10 = 5.
[spoiler title=”источники:”]
http://nauka.club/matematika/geometriya/srednyaya-liniya-treugolnika.html
[/spoiler]
