Как найти наибольшую сумму на отрезке - Сайт, где вы сможете решить свои вопросы

Задача нахождения максимума на отрезках фиксированной длины

Время на прочтение
3 мин

Количество просмотров 33K

Постановка задачи

Пусть дан массив A длины N, и дано число K ≤ N. Требуется найти максимум (минимум, сумма …) в подотрезках длины K данного массива. Это частный случай задачи RMQ (Range Minimum Query — минимум на отрезке), но с дополнительными ограничениями — постоянная длина отрезка поиска. В данном решении задача не предполагает возможность изменения элементов массива. Для определенности будем рассматривать нахождение максимума.

Преимущества и недостатки

Данный алгоритм позволяет находить максимум на подотрезках фиксированной длины за O(1), с препроцессингом за O(N). При этом вспомогательной памяти требуется 2*N. Но основным преимуществом можно считать очень простую реализацию и понятность. Недостаток – алгоритм не адаптирован для изменения элементов исходного массива. Т.е. изменение возможно, но для этого потребуется выполнить порядка O(K) действий.

Решение

Препроцессинг

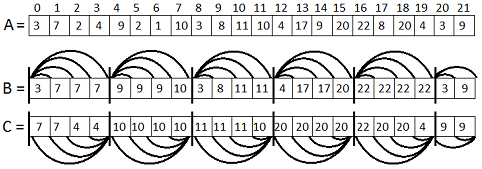
Разделим исходный массив A на блоки длиной K-1 (почему именно K-1, поймете чуть ниже). Затем рассчитаем два дополнительных массива B и C следующим образом:

в B[i] будем хранить максимум на промежутке от начала текущего блока до i-го элемента;
в C[i] будем хранить максимум на промежутке от i-го элемента до конца текущего блока.

Например в B[2] будем хранить максимум от A[0] до A[2], а в С[2] — максимум от A[2] до A[3]. Понятно, что эту операцию можно выполнить за O(n). На следующем рисунке приведен пример для N=22, K=5:

Обработка запроса

Теперь, с помощью этой нехитрой структуры, можно легко найти максимум на отрезке длины K. Мы специально сделали блоки длиной K-1, что бы края любого запроса всегда попадали в два соседних блока. И, следовательно, при любом запросе, в отрезок будет входить граница 2-х блоков. Назовем её T. Левый край отрезка — l, правый — r. Теперь для того что бы получить максимум, нам необходимо всего лишь взять max(C[l], B[r]). Действительно C[l] — это максимум на отрезке от l до T, а B[r] — максимум от T до r, и, следовательно, максимум от C[l] и B[r], будет максимумом на отрезке от l до r.

Реализация

Ниже приведена простейшая реализация на C++;


vector< int > B, C;

void
build(const vector< int > A, int k)
{
	int n = A.size();
	B.resize(n);
	C.resize(n);
	k--;

	// Расчитываем B
	for(int i = 0; i < n; i++)
	{
		if(i % k)
			B[i] = max(A[i], B[i - 1]);
		else
			B[i] = A[i];
	}

	
	// Расчитываем C
	C.back() = A.back();
	for(int i = n - 2; i >= 0; i--)
	{
		if((i + 1) % k)
			C[i] = max(A[i], C[i + 1]);
		else
			C[i] = A[i];
	}
		
}

int
GetMax(int l, int k)
{
	return max(C[l], B[l + k - 1]);
}

Для правильной работы так же необходимо что бы K, подаваемый на вход функций build и GetMax, был одинаковый.

Очевидно что данная реализация функции build не является оптимальной, однако она наиболее проста и понятна. На каждом следующем шаге вычисляется новое значение на основании предыдущего. Ниже приведена более скоростная реализация.


void
build(const vector< int > A, int k)
{
	int n = A.size();
	B.resize(n);
	C.resize(n);
	B.front() = A.front();
	C.back() = A.back();
	k--;

	for(int i1(1), i2(n - 2); i1 < n; i1++, i2--)
	{
		B[i1] = (i1 % k) ? max(A[i1], B[i1 - 1]) : A[i1];
		C[i2] = ((i2 + 1) % k) ? max(A[i2], C[i2 + 1]) : A[i2];
	}
}

Итог

Как видите алгоритм очень прост и в плане реализации, и в плане понимания. Он дает асимптотически лучшую оценку O(1) для поиска максимума на подотрезке заданной длины. Эту структуру легко изменить для поиска минимума или суммы. Кроме того максимальное количество возможных вариантов будет равно N-K, и значит, с помощью этой структуры можно посчитать все возможные комбинации за O(n). В каждый момент времени, в памяти нужно хранить только два соседних блока длиной K, что уменьшит размер памяти в более продвинутых реализациях.

Авторство алгоритма принадлежит Ван Херку.

Ссылки

Задача RMQ — 1. Static RMQ
Задача RMQ — 2. Дерево отрезков
Решение этой же задачи через модификацию стека (e-maxx)
Еще немного о RMQ (e-maxx)
Большое количество информации (на английском)

Источник

Дан целочисленный массив, найдите в нем непрерывный подмассив с наибольшей суммой.

Например,

Input: {-2, 1, -3, 4, -1, 2, 1, -5, 4}

Output: Subarray with the largest sum is {4, -1, 2, 1} with sum 6.

Потренируйтесь в этой проблеме

Задача отличается от задачи нахождения подпоследовательности максимальной суммы. В отличие от подпоследовательностей, подмассивы должны занимать последовательные позиции в исходном массиве.

Мы можем легко решить эту задачу за линейное время, используя Алгоритм Кадане. Идея состоит в том, чтобы поддерживать максимальный (с положительной суммой) подмассив, “заканчивающийся” на каждом индексе данного массива. Этот подмассив либо пуст (в этом случае его сумма равна нулю), либо состоит на один элемент больше, чем максимальный подмассив, оканчивающийся на предыдущем индексе.

Алгоритм может быть реализован следующим образом на C++, Java и Python:

C++

#include <iostream>

#include <vector>

using namespace std;

// Функция для нахождения максимальной суммы непрерывного подмассива

// в заданном целочисленном массиве

int kadane(vector<int> const &arr)

{

// сохраняет максимальный суммарный подмассив, найденный на данный момент

int max_so_far = 0;

// сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции

int max_ending_here = 0;

// обход заданного массива

for (int i = 0; i < arr.size(); i++)

{

// обновить максимальную сумму подмассива, “заканчивающегося” на индексе “i” (путем добавления

// текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’)

max_ending_here = max_ending_here + arr[i];

// если максимальная сумма отрицательна, устанавливаем ее в 0 (что представляет

// пустой подмассив)

max_ending_here = max(max_ending_here, 0);

// обновить результат, если текущая сумма подмассива окажется больше

max_so_far = max(max_so_far, max_ending_here);

}

return max_so_far;

}

int main()

{

vector<int> arr = { –2, 1, –3, 4, –1, 2, 1, –5, 4 };

cout << “The maximum sum of a contiguous subarray is “ << kadane(arr);

return 0;

}

Скачать Выполнить код

результат:

The maximum sum of a contiguous subarray is 6

Java

class Main

{

// Функция для нахождения максимальной суммы непрерывного подмассива

// в заданном целочисленном массиве

public static int kadane(int[] arr)

{

// сохраняет максимальный суммарный подмассив, найденный на данный момент

int maxSoFar = 0;

// сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции

int maxEndingHere = 0;

// обход заданного массива

for (int i: arr)

{

// обновить максимальную сумму подмассива, “заканчивающегося” на индексе “i” (путем добавления

// текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’)

maxEndingHere = maxEndingHere + i;

// если максимальная сумма отрицательна, устанавливаем ее в 0 (что представляет

// пустой подмассив)

maxEndingHere = Integer.max(maxEndingHere, 0);

// обновить результат, если текущая сумма подмассива окажется больше

maxSoFar = Integer.max(maxSoFar, maxEndingHere);

}

return maxSoFar;

}

public static void main(String[] args)

{

int[] arr = { –2, 1, –3, 4, –1, 2, 1, –5, 4 };

System.out.println(“The sum of contiguous subarray with the “ +

“largest sum is “ + kadane(arr));

}

Скачать Выполнить код

результат:

The maximum sum of a contiguous subarray is 6

Python

# Функция нахождения максимальной суммы непрерывного подмассива

# в заданном целочисленном массиве

def kadane(arr):

# хранит подсписок максимальной суммы, найденный на данный момент.

max_so_far = 0

# хранит максимальную сумму подсписков, заканчивающихся на текущей позиции

max_ending_here = 0

# пройти по заданному списку

for i in arr:

# обновляет максимальную сумму подсписка, «заканчивающегося» на индексе «i» (путем добавления

# текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’)

max_ending_here = max_ending_here + i

#, если максимальная сумма отрицательна, установите ее на 0 (что означает

# пустой подсписок)

max_ending_here = max(max_ending_here, 0)

# обновляет результат, если сумма текущего подсписка оказывается больше

max_so_far = max(max_so_far, max_ending_here)

return max_so_far

if __name__ == ‘__main__’:

arr = [–2, 1, –3, 4, –1, 2, 1, –5, 4]

print(‘The sum of contiguous sublist with the largest sum is’,

kadane(arr))

Скачать Выполнить код

результат:

The maximum sum of a contiguous subarray is 6

Временная сложность приведенного выше решения равна O(n) и не требует дополнительного места, где n это размер ввода.

Приведенный выше код не обрабатывает случай, когда все элементы массива отрицательные. Если массив содержит все отрицательные значения, ответом является максимальный элемент. Мы можем легко разместить эту проверку перед тем, как продолжить алгоритм. Реализацию можно увидеть ниже на C++, Java и Python:

C++

#include <iostream>

#include <vector>

#include <algorithm>

using namespace std;

// Функция для нахождения максимальной суммы непрерывного подмассива

// в заданном целочисленном массиве

int kadane(vector<int> const &arr)

{

// находим максимальный элемент в заданном массиве

int max_num = *max_element(arr.begin(), arr.end());

// если массив содержит все отрицательные значения, вернуть максимальный элемент

if (max_num < 0) {

return max_num;

}

// сохраняет максимальный суммарный подмассив, найденный на данный момент

int max_so_far = 0;

// сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции

int max_ending_here = 0;

// обход заданного массива

for (int i = 0; i < arr.size(); i++)

{

// обновить максимальную сумму подмассива, “заканчивающегося” на индексе “i” (путем добавления

// текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’)

max_ending_here = max_ending_here + arr[i];

// если максимальная сумма отрицательна, устанавливаем ее в 0 (что представляет

// пустой подмассив)

max_ending_here = max(max_ending_here, 0);

// обновить результат, если текущая сумма подмассива окажется больше

max_so_far = max(max_so_far, max_ending_here);

}

return max_so_far;

}

int main()

{

vector<int> arr = { –8, –3, –6, –2, –5, –4 };

cout << “The maximum sum of a contiguous subarray is “ << kadane(arr);

return 0;

}

Скачать Выполнить код

результат:

The maximum sum of a contiguous subarray is -2

Java

import java.util.Arrays;

class Main

{

// Функция для нахождения максимальной суммы непрерывного подмассива

// в заданном целочисленном массиве

public static int kadane(int[] arr)

{

// находим максимальный элемент в заданном массиве

int max = Arrays.stream(arr).max().getAsInt();

// если массив содержит все отрицательные значения, вернуть максимальный элемент

if (max < 0) {

return max;

}

// сохраняет максимальный суммарный подмассив, найденный на данный момент

int maxSoFar = 0;

// сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции

int maxEndingHere = 0;

// делаем для каждого элемента заданного массива

for (int i: arr)

{

// обновить максимальную сумму подмассива, “заканчивающегося” на индексе “i” (путем добавления

// текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’)

maxEndingHere = maxEndingHere + i;

// если максимальная сумма отрицательна, устанавливаем ее в 0 (что представляет

// пустой подмассив)

maxEndingHere = Integer.max(maxEndingHere, 0);

// обновить результат, если текущая сумма подмассива окажется больше

maxSoFar = Integer.max(maxSoFar, maxEndingHere);

}

return maxSoFar;

}

public static void main(String[] args)

{

int[] arr = { –8, –3, –6, –2, –5, –4 };

System.out.println(“The sum of contiguous subarray with the “ +

“largest sum is “ + kadane(arr));

}

Скачать Выполнить код

результат:

The maximum sum of a contiguous subarray is -2

Python

# Функция нахождения максимальной суммы непрерывного подмассива

# в заданном целочисленном массиве

def kadane(arr):

# найти максимальный элемент, присутствующий в данном списке

maximum = max(arr)

#, если список содержит все отрицательные значения, вернуть максимальный элемент

if maximum < 0:

return maximum

# хранит подсписок максимальной суммы, найденный на данный момент.

max_so_far = 0

# хранит максимальную сумму подсписков, заканчивающихся на текущей позиции

max_ending_here = 0

# сделать для каждого элемента заданного списка

for i in arr:

# обновляет максимальную сумму подсписка, «заканчивающегося» на индексе «i» (путем добавления

# текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’)

max_ending_here = max_ending_here + i

#, если максимальная сумма отрицательна, установите ее на 0 (что означает

# пустой подсписок)

max_ending_here = max(max_ending_here, 0)

# обновляет результат, если сумма текущего подсписка оказывается больше

max_so_far = max(max_so_far, max_ending_here)

return max_so_far

if __name__ == ‘__main__’:

arr = [–8, –3, –6, –2, –5, –4]

print(‘The sum of contiguous sublist with the largest sum is’, kadane(arr))

Скачать Выполнить код

результат:

The maximum sum of a contiguous subarray is -2

Этот подход требует двух обходов входного массива. Мы можем легко модифицировать основной алгоритм, чтобы он обрабатывал и отрицательные целые числа. Алгоритм может быть реализован следующим образом на C++, Java и Python:

C++

#include <iostream>

#include <vector>

#include <climits>

using namespace std;

// Функция для нахождения максимальной суммы непрерывного подмассива

// в заданном целочисленном массиве (также обрабатывает отрицательные числа)

int kadaneNeg(vector<int> const &arr)

{

// сохраняет максимальный суммарный подмассив, найденный на данный момент

int max_so_far = INT_MIN;

// сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции

int max_ending_here = 0;

// обход заданного массива

for (int i = 1; i < arr.size(); i++)

{

// обновить максимальную сумму подмассива, “заканчивающегося” на индексе “i” (путем добавления

// текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’)

max_ending_here = max_ending_here + arr[i];

// максимальная сумма должна быть больше текущего элемента

max_ending_here = max(max_ending_here, arr[i]);

// обновить результат, если текущая сумма подмассива окажется больше

max_so_far = max(max_so_far, max_ending_here);

}

return max_so_far;

}

int main()

{

vector<int> arr = { –8, –3, –6, –2, –5, –4 };

cout << “The maximum sum of a contiguous subarray is “ << kadaneNeg(arr);

return 0;

}

Скачать Выполнить код

результат:

The maximum sum of a contiguous subarray is -2

Java

class Main

{

// Функция для нахождения максимальной суммы непрерывного подмассива

// в заданном целочисленном массиве (также обрабатывает отрицательные числа)

public static int kadaneNeg(int[] arr)

{

// сохраняет максимальный суммарный подмассив, найденный на данный момент

int maxSoFar = Integer.MIN_VALUE;

// сохраняет максимальную сумму подмассива, заканчивающегося на текущей позиции

int maxEndingHere = 0;

// обход заданного массива

for (int i: arr)

{

// обновить максимальную сумму подмассива, “заканчивающегося” на индексе “i” (путем добавления

// текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе)

maxEndingHere = maxEndingHere + i;

// максимальная сумма должна быть больше текущего элемента

maxEndingHere = Integer.max(maxEndingHere, i);

// обновить результат, если текущая сумма подмассива окажется больше

maxSoFar = Integer.max(maxSoFar, maxEndingHere);

}

return maxSoFar;

}

public static void main(String[] args)

{

int[] arr = { –8, –3, –6, –2, –5, –4 };

System.out.println(“The maximum sum of a contiguous subarray is “ +

kadaneNeg(arr));

}

Скачать Выполнить код

результат:

The maximum sum of a contiguous subarray is -2

Python

import sys

# Функция нахождения максимальной суммы непрерывного подмассива

# в заданном целочисленном массиве (также обрабатывает отрицательные числа)

def kadaneNeg(arr):

# хранит подсписок максимальной суммы, найденный на данный момент.

max_so_far = –sys.maxsize

# хранит максимальную сумму подсписков, заканчивающихся на текущей позиции

max_ending_here = 0

# пройти по заданному списку

for i in range(len(arr)):

# обновляет максимальную сумму подсписка, «заканчивающегося» на индексе «i» (путем добавления

# текущий элемент до максимальной суммы, заканчивающейся на предыдущем индексе ‘i-1’)

max_ending_here = max_ending_here + arr[i]

# Максимальная сумма # должна быть больше, чем текущий элемент

max_ending_here = max(max_ending_here, arr[i])

# обновляет результат, если сумма текущего подсписка оказывается больше

max_so_far = max(max_so_far, max_ending_here)

return max_so_far

if __name__ == ‘__main__’:

arr = [–8, –3, –6, –2, –5, –4]

print(‘The sum of contiguous sublist with the largest sum is’, kadaneNeg(arr))

Скачать Выполнить код

результат:

The maximum sum of a contiguous subarray is -2

Из-за того, как этот алгоритм использует оптимальные основания (максимальный подмассив, заканчивающийся в каждой позиции, вычисляется просто из связанной, но меньшей и перекрывающейся подзадачи: максимальный подмассив, заканчивающийся в предыдущей позиции), этот алгоритм можно рассматривать как простой пример динамическое программирование.

Связанный пост:

Вывести непрерывный подмассив с максимальной суммой

Использованная литература: https://en.wikipedia.org/wiki/Maximum_subarray_problem

Источник

Онлайн калькулятор для нахождения наибольшего значения функции на отрезке в заданном интервале. Вычислить точки наибольшего значения функции.

Для примера рассмотрим нахождение f(x)=x(x-3)^2 максимального значения точки графика функции на отрезке от -2 до 5. Результат = 20.
Вам может понадобиться калькулятор для нахождения наименьшего значения функции.

Синтаксис
основных функций:
x^a: x^a
|x|: abs(x)
√x: Sqrt[x]
ⁿ√x: x^(1/n)
a^x: a^x
log^ax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]

sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]

arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]

areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Источник

Рассмотрим элемент a_i и некоторый отрезок [j..i] (то есть отрезок, для которого элемент a_i является последним). По условию нас интересуют только отрезки, у которых a_j == a_i. Поймём, какой из таких отрезков даёт наибольшую сумму. Распишем сумму отрезка (нумерация элементов в массиве с единицы):

sum([j..i]) = sum([1..i]) - sum([1..(j-1)])

Таким образом, для фиксированного i достаточно найти такой j, что sum([1..(j-1)]) минимальна. Это можно сделать с помощью хеш-таблицы, в которой для каждого числа a_i будем хранить минимальную из сумм sum([1..(j-1)]) для всех подходящих j.

typedef long long ll;

// для удобства добавим в начало массива ноль
vector<int> a = {0 /* extra zero */, 3, 5, 6, 3, 5};
// элементы массива индексируются [1..n]
int n = a.size() - 1;

// префиксные суммы
// cumsum[k] := a[1] + ... + a[k]
vector<ll> prefixSums;
for (int ai : a)
    prefixSums.push_back(prefixSums.empty() ? 0 : prefixSums.back() + ai);

// сумма на отрезке a_j ... a_i равна сумме на префиксе [1..i] минус сумме на префиксе [1..j-1]
// по условию задачи рассматриваются только такие суммы, что a_j == a_i
// будем итерироваться по массиву и для каждого числа a_j запоминать минимальную сумму на префиксе [1..j-1]
// при встрече очередного числа a_i будем обновлять ответ, рассматривая отрезок [j..i]
unordered_map<int, ll> numberToMinSum;
ll answer = numeric_limits<ll>::min();
for (int i = 1; i <= n; ++i) {
    if (numberToMinSum.find(a[i]) != numberToMinSum.end()) {
        numberToMinSum[a[i]] = min(numberToMinSum[a[i]], prefixSums[i - 1]);
        answer = max(answer, prefixSums[i] - numberToMinSum[a[i]]);
    } else {
        numberToMinSum[a[i]] = prefixSums[i - 1];
    }
}
cout << answer << endl;

Проверка на Ideone.

Источник

Задача нахождения максимума на отрезках фиксированной длины

Постановка задачи

Преимущества и недостатки

Решение

Препроцессинг

Обработка запроса

Реализация

Итог

Авторство алгоритма принадлежит Ван Херку.

Ссылки

C++

Java

Python

C++

Java

Python

C++

Java

Python

Вам также может понравиться

Как составить договор на повышение квалификации

Как найти пару к взаимно обратным числам

Как найти недавно удаленный документ

Добавить комментарий Отменить ответ