Наименьшее о́бщее кратное (HOK) двух целых чисел — это наименьшее натуральное число, которое делится на оба без остатка, то есть кратно им обоим. К примеру, для чисел 6 и 4, наименьшим общим кратным будет 12.
Как найти НОК?
Способов найти НОК несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОК при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:
- разложить оба числа на простые множители;
- выбрать одну группу множителей;
- добавить к ним множители из второй группы, которые отсутствуют в выбранной;
- найти их произведение.
Примеры нахождения наименьшего общего кратного
Рассмотрим приведенный алгоритм на конкретных примерах:
Пример 1: найти НОК 4 и 6
1. Раскладываем 6 и 4 на простые множители:
2. Возьмем первую группу множителей: 2 · 3.
3. Смотрим вторую группу (2 · 2) и видим, что из двух двоек, одна присутствует в первом разложении. Таким образом, берем только одну двойку. Добавляем к первому разложению и получаем: 2 · 3 · 2
4. Вычисляем произведение: 2 · 3 · 2 = 12.
Ответ: НОК (6; 4) = 12
Пример 2: найти НОК 32 и 20
1. Раскладываем 32 и 20 на простые множители:
2. Возьмем первую группу множителей: 2 · 2 · 2 · 2 · 2.
3. Смотрим вторую группу (2 · 2 · 5) и видим, что из двух двоек и пятерки, обе двойки присутствуют в первом разложении. Таким образом, берем только пятерку. Добавляем к первому разложению и получаем: 2 · 3 · 2
4. Вычисляем произведение: 2 · 2 · 2 · 2 · 2 · 5 = 160.
Ответ: НОК (32; 20) = 160
Что такое кратное число
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.
Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.
Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.
Кратное число — это …
Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.
Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).
А у чисел, которые участвуют в делении, есть определенные названия:
- Делимое – то число, которое собираются делить;
- Делитель – число, на которое будут делить делимое. Соответственно, делитель чаще всего меньше делимого. Хотя не исключен и другой вариант. Единственное число, которое не может быть делителем, это ноль.
- Частное – результат деления, то есть число, которое получается в результате выполнения математического действия.
Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.

Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.
Одно число называется кратным другому, если его можно на него поделить без остатка.

Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.
Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.
12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6
Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.
Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:
Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.
Таблицы чисел кратных 2,3,4,5,6,7,9
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.
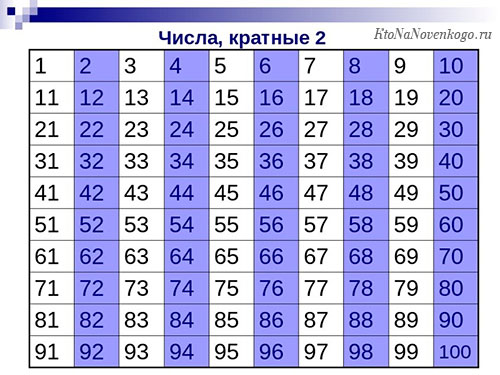
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.
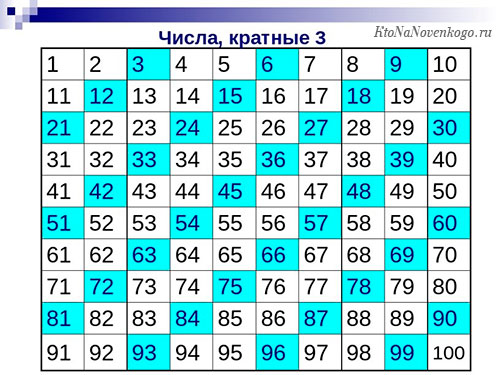
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.
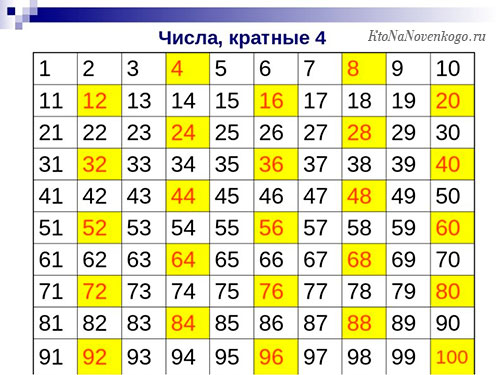
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.
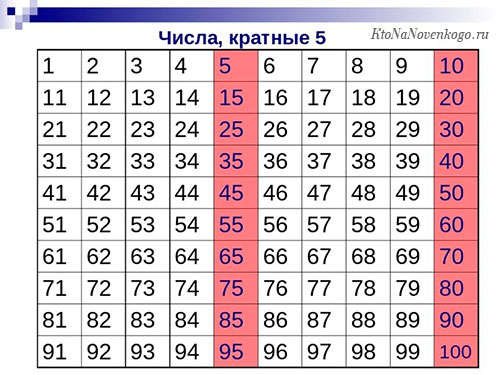
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.
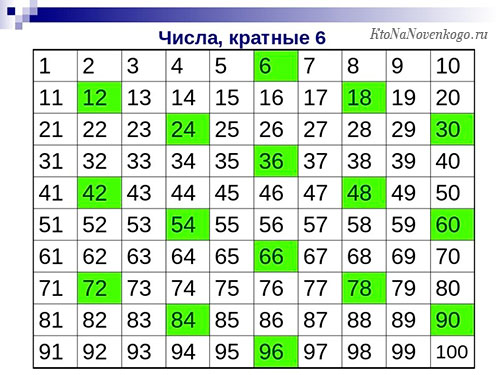
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».
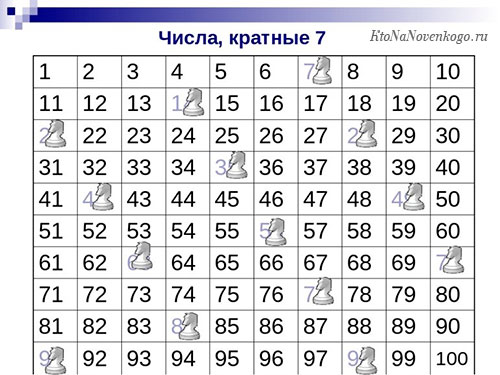
И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.
Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.
| Числа, кратные 9 | 27 | 198 | 5 877 | 3 816 | 117 | 72 |
|---|---|---|---|---|---|---|
| Сумма | 9 | 18 | 27 | 18 | 9 | 9 |
Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.
Вместо заключения
А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.
Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.
Что такое нок в математике? Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы узнаем, как найти наименьшее общее кратное, какие есть для этого способы для трех чисел и более, разберем вопрос о том, как находить НОК отрицательного числа. Также разберемся, что такое нок и нод, как найти нок и нод.
Вычисление наименьшего общего кратного (НОК) через НОД
Мы уже узнали, что такое нок, а также установили связь наименьшего общего кратного с наибольшим общим делителем (кратность показывает в расчетах во сколько раз один показатель больше другого). Теперь как настоящие математики научимся определять НОК через НОД (нок и нод чисел натуральных). Сначала разберемся, как найти нок для положительных чисел. Сделать это можно и онлайн или на калькуляторе, но лучше научиться самостоятельно.
Поиск наименьшего общего кратного через наибольший общий делитель можно по формуле НОК(a, b)=a·b:НОД(a, b).
Необходимо найти НОК чисел 126 и 70.
Решение
Начнем решать. Примем a=126, b=70. Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК(a, b)=a·b:НОД(a, b).
Найдем НОД чисел 70 и 126. Для этого нам понадобится алгоритм Евклида: 126=70·1+56, 70=56·1+14, 56=14·4, следовательно, NOD(126, 70)=14.
Вычислим НОК: НОК(126, 70)=126·70:НОД(126, 70)=126·70:14=630.
Ответ: NOC(126, 70)=630.
Найдите нок чисел 68 и 34.
Решение
Как находить нод? НОД в данном случае нейти несложно, так как 68 делится на 34. Вычислим самое маленькое общее кратное по формуле: НОК(68, 34)=68·34:НОД(68, 34)=68·34:34=68.
Ответ: НОК(68, 34)=68.
В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.
Нахождение НОК с помощью разложения чисел на простые множители
Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители. Перед тем, как это узнавать, дадим небольшое определение.
Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:
- составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
- исключаем их полученных произведений все простые множители;
- полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.
Этот способ нахождения наименьшего общего кратного основан на равенстве НОК(a, b)=a·b:НОД(a, b). Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.
У нас есть два числа 75 и 210. Мы можем разложить их на множители следующим образом: 75=3·5·5 и 210=2·3·5·7. Если составить произведение всех множителей двух исходных чисел, то получится: 2·3·3·5·5·5·7.
Если исключить общие для обоих чисел множители 3 и 5, мы получим произведение следующего вида: 2·3·5·5·7=1050. Это произведение и будет нашим НОК для чисел 75 и 210.
Найдите НОК чисел 441 и 700, разложив оба числа на простые множители.
Решение
Найдем все простые множители чисел, данных в условии:
44114749713377
700350175357122557
Получаем две цепочки чисел: 441=3·3·7·7 и 700=2·2·5·5·7.
Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2·2·3·3·5·5·7·7·7. Найдем общие множители. Это число 7. Исключим его из общего произведения: 2·2·3·3·5·5·7·7. Получается, что НОК(441, 700)=2·2·3·3·5·5·7·7=44 100.
Ответ: НОК(441, 700)= 44 100.
Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.
Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:
- разложим оба числа на простые множители:
- добавим к произведению простых множителей первого числа недостающие множители второго числа;
- получим произведение, которое и будет искомым НОК двух чисел.
Вернемся к числам 75 и 210, для которых мы уже пробовали искать НОК в одном из прошлых примеров. Разложим их на простые множители: 75=3·5·5 и 210=2·3·5·7. К произведению множителей 3, 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210. Получаем: 2·3·5·5·7. Это и есть НОК чисел 75 и 210.
Необходимо вычислить НОК чисел 84 и 648.
Решение
Разложим числа из условия на простые множители: 84=2·2·3·7 и 648=2·2·2·3·3·3·3. Добавим к произведению множителей 2, 2, 3 и 7 числа 84 недостающие множители 2, 3, 3 и
3 числа 648. Получаем произведение 2·2·2·3·3·3·3·7=4536. Это и есть наименьшее общее кратное чисел 84 и 648 .
Ответ: НОК(84, 648)=4 536.
Нахождение НОК трех и большего количества чисел
Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.
Предположим, что у нас есть целые числа a1, a2, …, ak. НОК mk этих чисел находится при последовательном вычислении m2=НОК(a1, a2), m3=НОК(m2, a3), …, mk=НОК(mk−1, ak).
Теперь рассмотрим, как можно применять теорему для решения конкретных задач.
Необходимо вычислить наименьшее общее кратное четырех чисел 140, 9, 54 и 250.
Решение задания
Введем обозначения: a1=140, a2=9, a3=54, a4=250.
Начнем с того, что вычислим m2=НОК(a1, a2)=НОК(140, 9). Применим алгоритм Евклида для вычисления НОД чисел 140 и 9: 140=9·15+5, 9=5·1+4, 5=4·1+1, 4=1·4. Получаем: НОД(140, 9)=1, НОК(140, 9)=140·9:НОД(140, 9)=140·9:1=1 260. Следовательно, m2=1 260.
Теперь вычислим по тому е алгоритму m3=НОК(m2, a3)=НОК(1 260, 54). В ходе вычислений получаем m3=3 780.
Нам осталось вычислить m4=НОК(m3, a4)=НОК(3 780, 250). Действуем по тому же алгоритму. Получаем m4=94 500.
НОК четырех чисел из условия примера равно 94500.
Ответ: НОК(140, 9, 54, 250)=94 500.
Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.
Предлагаем вам следующий алгоритм действий:
- раскладываем все числа на простые множители;
- к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
- к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
- полученное произведение будет наименьшим общим кратным всех чисел из условия.
Необходимо найти НОК пяти чисел 84, 6, 48, 7, 143.
Решение
Разложим все пять чисел на простые множители: 84=2·2·3·7, 6=2·3, 48=2·2·2·2·3, 7, 143=11·13. Простые числа, которым является число 7, на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.
Теперь возьмем произведение простых множителей 2, 2, 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3. Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.
Продолжаем добавлять недостающие множители. Переходим к числу 48, из произведения простых множителей которого берем 2 и 2. Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2·2·2·2·3·7·11·13=48 048. Это и есть наименьшее общее кратное пяти исходных чисел.
Ответ: НОК(84, 6, 48, 7, 143)=48 048.
Нахождение наименьшего общего кратного отрицательных чисел
Для того чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.
НОК(54, −34)=НОК(54, 34), а НОК(−622, −46, −54, −888)=НОК(622, 46, 54, 888).
Такие действия допустимы в связи с тем, что если принять, что a и −a – противоположные числа,
то множество кратных числа a совпадает со множеством кратных числа −a.
Необходимо вычислить НОК отрицательных чисел −145 и −45.
Решение
Произведем замену чисел −145 и −45 на противоположные им числа 145 и 45. Теперь по алгоритму вычислим НОК(145, 45)=145·45:НОД(145, 45)=145·45:5=1 305, предварительно определив НОД по алгоритму Евклида.
Получим, что НОК чисел −145 и −45 равно 1 305.
Ответ: НОК(−145, −45)=1 305.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Содержание:
- Определение кратного числа
- Некоторые признаки делимости натуральных чисел
- Наименьшее общее кратное (НОК)
Определение кратного числа
Определение
Число $n$ называется кратным
некоторому натуральному числу $p$, если оно нацело
делится на $p$. При этом говорят что
$n$ кратно
$p$ .
Некоторые признаки делимости натуральных чисел
-
Признак делимости на 2.
Число делится на 2, если его последняя цифра есть число четное (то есть 2, 4, 6, 8) или 0.
-
Признак делимости на 3.
Число делится на 3, если сумма его цифр делится на 3.
-
Признак делимости на 4.
Число делится на 4, если две его последние цифры – нули или образуют число, делящееся на 4.
-
Признак делимости на 5.
Число делится на 5, если оно заканчивается либо на 0, либо на 5.
-
Признак делимости на 8.
Число делится на 8, если три его последние цифры – нули или образуют число, делящееся на 8.
-
Признак делимости на 9.
Число делится на 9, если сумма его цифр делится на 9.
-
Признак делимости на 11.
Число делится на 11, если сумма цифр, стоящих на четных местах либо равна сумме цифр,
стоящих на нечетных местах, либо отличается от неё на число, делящееся на 11. -
Признак делимости на 25.
Число делится на 5, если две его последние цифры – нули или образуют число, делящееся на 25.
Пример
Задание. Среди ниже перечисленных чисел выбрать числа кратные 3:
$$27: 36 ; 58 ; 1119 ; 2345 ; 12354$$
Решение. Будем использовать признак делимости на 3, для этого найдем сумму цифр для каждого числа:
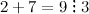 ;
;
 ;
;

 ;
;

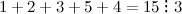
Таким образом, на 3 делятся числа:
$$27 ; 36 ; 1119: 12354$$
Ответ. $27 ; 36 ; 1119: 12354$
Наименьшее общее кратное (НОК)
Определение
Общим кратным нескольких натуральных чисел называется натуральное число, являющееся кратным для каждого
из них. Наименьшее из всех кратных называется наименьшим общим кратным (НОК).
Алгоритм нахождения наименьшего общего кратного нескольких чисел:
- выписать каноническое разложение данных чисел;
- перечислить все простые множители, входящие в канонические разложения данных чисел;
- возвести каждый множитель в наибольшую степень, с которой он входит в каноническое разложение данных чисел.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти НОК(360; 420)
Решение. Запишем каноническое разложение заданных чисел:
$360 = 2^3 cdot 3^2 cdot 5$ и
$420 = 2^2 cdot 3 cdot 5 cdot 7$
Выпишем все простые множители, которые входят в каноническое разложение заданных чисел:
$2; 3; 5; 7$ . И возведем их в наибольшую степень,
с которой они входят в разложения этих чисел. Получим
НОК(360; 420) $=2^{3} cdot 3^{2} cdot 5 cdot 7=2520$
Ответ. НОК(360; 420) $=2520$
Читать дальше: что такое степень числа.
Загрузить PDF
Загрузить PDF
Кратное число – это число, которое делится на данное число без остатка. Наименьшее общее кратное (НОК) группы чисел – это наименьшее число, которое делится без остатка на каждое число группы. Чтобы найти наименьшее общее кратное, нужно найти простые множители данных чисел. Также НОК можно вычислить с помощью ряда других методов, которые применимы к группам из двух и более чисел.
-

1
Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых меньше 10. Если даны большие числа, воспользуйтесь другим методом.
- Например, найдите наименьшее общее кратное чисел 5 и 8. Это небольшие числа, поэтому можно использовать данный метод.
-

2
Запишите ряд чисел, которые кратны первому числу. Кратное число – это число, которое делится на данное число без остатка.[1]
Кратные числа можно посмотреть в таблице умножения..- Например, числами, которые кратны 5, являются: 5, 10, 15, 20, 25, 30, 35, 40.
-

3
Запишите ряд чисел, которые кратны первому числу. Сделайте это под кратными числами первого числа, чтобы сравнить два ряда чисел.
- Например, числами, которые кратны 8, являются: 8, 16, 24, 32, 40, 48, 56, и 64.
-

4
Найдите наименьшее число, которое присутствует в обоих рядах кратных чисел. Возможно, вам придется написать длинные ряды кратных чисел, чтобы найти общее число. Наименьшее число, которое присутствует в обоих рядах кратных чисел, является наименьшим общим кратным.[2]
- Например, наименьшим числом, которое присутствует в рядах кратных чисел 5 и 8, является число 40. Поэтому 40 – это наименьшее общее кратное чисел 5 и 8.
Реклама
-

1
Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых больше 10. Если даны меньшие числа, воспользуйтесь другим методом.
- Например, найдите наименьшее общее кратное чисел 20 и 84. Каждое из чисел больше 10, поэтому можно использовать данный метод.
-

2
Разложите на простые множители первое число. То есть нужно найти такие простые числа, при перемножении которых получится данное число. Найдя простые множители, запишите их в виде равенства.
-

3
Разложите на простые множители второе число. Сделайте это так же, как вы раскладывали на множители первое число, то есть найдите такие простые числа, при перемножении которых получится данное число.
-

4
Запишите множители, общие для обоих чисел. Запишите такие множители в виде операции умножения. По мере записи каждого множителя зачеркивайте его в обоих выражениях (выражения, которые описывают разложения чисел на простые множители).
- Например, общим для обоих чисел является множитель 2, поэтому напишите
и зачеркните 2 в обоих выражениях.
- Общим для обоих чисел является еще один множитель 2, поэтому напишите
и зачеркните вторую 2 в обоих выражениях.
- Например, общим для обоих чисел является множитель 2, поэтому напишите
-

5
К операции умножения добавьте оставшиеся множители. Это множители, которые не зачеркнуты в обоих выражениях, то есть множители, не являющиеся общими для обоих чисел.[3]
-

6
Вычислите наименьшее общее кратное. Для этого перемножьте числа в записанной операции умножения.
- Например,
. Таким образом, наименьшее общее кратное 20 и 84 равно 420.
Реклама
- Например,
-

1
Нарисуйте сетку как для игры в крестики-нолики. Такая сетка представляет собой две параллельные прямые, которые пересекаются (под прямым углом) с другими двумя параллельными прямыми. Таким образом, получатся три строки и три столбца (сетка очень похожа на значок #). Первое число напишите в первой строке и втором столбце. Второе число напишите в первой строке и третьем столбце.[4]
- Например, найдите наименьшее общее кратное чисел 18 и 30. Число 18 напишите в первой строке и втором столбце, а число 30 напишите в первой строке и третьем столбце.
-

2
Найдите делитель, общий для обоих чисел. Запишите его в первой строке и первом столбце. Лучше искать простые делители, но это не является обязательным условием.
- Например, 18 и 30 – это четные числа, поэтому их общим делителем будет число 2. Таким образом, напишите 2 в первой строке и первом столбце.
-

3
Разделите каждое число на первый делитель. Каждое частное запишите под соответствующим числом. Частное – это результат деления двух чисел.
- Например,
, поэтому запишите 9 под 18.
-
, поэтому запишите 15 под 30.
- Например,
-

4
Найдите делитель, общий для обоих частных. Если такого делителя нет, пропустите два следующих шага. В противном случае делитель запишите во второй строке и первом столбце.
- Например, 9 и 15 делятся на 3, поэтому запишите 3 во второй строке и первом столбце.
-

5
Разделите каждое частное на второй делитель. Каждый результат деления запишите под соответствующим частным.
- Например,
, поэтому запишите 3 под 9.
-
, поэтому запишите 5 под 15.
- Например,
-

6
Если нужно, дополните сетку дополнительными ячейками. Повторяйте описанные действия до тех пор, пока у частных не будет общего делителя.
-

7
Обведите кружками числа в первом столбце и последней строке сетки. Затем выделенные числа запишите в виде операции умножения.[5]
- Например, числа 2 и 3 находятся в первом столбце, а числа 3 и 5 находятся в последней строке, поэтому операцию умножения запишите так:
.
- Например, числа 2 и 3 находятся в первом столбце, а числа 3 и 5 находятся в последней строке, поэтому операцию умножения запишите так:
-

8
Найдите результат умножения чисел. Так вы вычислите наименьшее общее кратное двух данных чисел.[6]
- Например,
. Таким образом, наименьшее общее кратное 18 и 30 равно 90.
Реклама
- Например,
-

1
Запомните терминологию, связанную с операцией деления. Делимое – это число, которое делят. Делитель – это число, на которое делят. Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел.[7]
- Например, в выражении
ост. 3:
15 – это делимое
6 – это делитель
2 – это частное
3 – это остаток.
- Например, в выражении
-

2
Запишите выражение, которое описывает операцию деления с остатком. Выражение:
.[8]
Это выражение будет использовано, чтобы записать алгоритм Евклида и найти наибольший общий делитель двух чисел.- Например,
.
- Наибольший общий делитель (НОД) – это наибольшее число, на которое делятся все данные числа.[9]
- В этом методе сначала нужно найти наибольший общий делитель, а затем вычислить наименьшее общее кратное.
- Например,
-

3
Большее из двух чисел рассматривайте в качестве делимого. Меньшее из двух чисел считайте делителем. Для этих чисел запишите выражение, которое описывает операцию деления с остатком.
- Например, найдите наименьшее общее кратное чисел 210 и 45. Запишите такое выражение:
.
- Например, найдите наименьшее общее кратное чисел 210 и 45. Запишите такое выражение:
-

4
Первый делитель превратите в новое делимое. Остаток используйте в качестве нового делителя. Для этих чисел запишите выражение, которое описывает операцию деления с остатком.
- Например,
.
- Например,
-

5
Повторяйте описанные действия до тех пор, пока остаток не будет равен 0. Предыдущий делитель используйте в качестве нового делимого, а предыдущий остаток – как новый делитель; для этих чисел записывайте соответствующее выражение.[10]
- Например,
. Так как остаток равен 0, дальше делить нельзя.
- Например,
-

6
Посмотрите на последний делитель. Это наибольший общий делитель двух чисел.[11]
- Например, последним выражением было
, поэтому последний делитель – это число 15. Таким образом, 15 – это наибольший общий делитель чисел 210 и 45.
- Например, последним выражением было
-
7
Перемножьте два числа. Затем разделите произведение на наибольший общий делитель. Так вы вычислите наименьшее общее кратное двух чисел.[12]
[[[Image:Find the Least Common Multiple of Two Numbers Step 25.jpg|center]]Реклама
Советы
- Если нужно найти НОК трех и более чисел, упросите себе задачу. Например, чтобы вычислить НОК чисел 16, 20 и 32, сначала найдите наименьшее общее кратное чисел 16 и 20 (оно равно 80), а потом найдите НОК чисел 80 и 32, которое равно 160.
- НОК имеет множество применений. Например, чтобы сложить или вычесть дроби, они должны иметь одинаковый знаменатель. Если у дробей разные знаменатели, нужно преобразовать дроби так, чтобы привести их к общему знаменателю. А это проще сделать, если найти наименьший общий знаменатель, который равен наименьшему общему кратному чисел, которые находятся в знаменателях дробей.
Реклама
Об этой статье
Эту страницу просматривали 69 143 раза.
