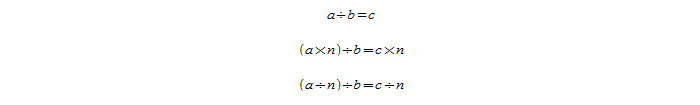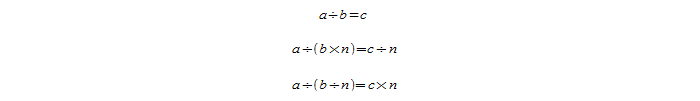Содержание материала
- Определение частного чисел (деление)
- Видео
- Неполное частное
- Как найти частное чисел
- Проверка деления умножением
- Увеличение или уменьшение делимого
- Нахождение значения частного чисел
- Деление с остатком
Определение частного чисел (деление)
Частное чисел — это результат получаемый при определении количества содержания одного числа в другом. Проще говоря это обычное деление. При этом общепринятые оперируемые понятия для частного это делимое, делитель и само частное — результат.
Пример. Найти частное чисел:
1) 20:2=10;
2) 35:7=5.
Ответ: 20:2=10 и 35:7=5.
Это был самый простой пример. Все самое интересное впереди! Проблемы с делением начинаются тогда, когда числа становятся большими и выходят за рамки таблицы умножения. Здесь приходится делить большое число по определенному правилу. Такое деление еще называется деление в столбик.
Пример. Найти частное чисел:
1) 894:3=298
-894| 3__ 6 |298-29 27— 24 24 0
Ответ: 894:3=298
Видео
Неполное частное
Неполное частное – результат, который получился после деления с остатком.
Под делением с остатком понимается нахождение наибольшего целого числа, которое в произведении с делителем дает число, не превышающее делимое. Это искомое и называют неполным частным.
Разность между делимым и произведением делителя на неполное частное называется остатком, который всегда меньше делителя.
Например, 17 не делится без остатка на 5.
Наибольшее число, результат умножения которого на 5 не превосходит 17, это 3. 3 в данном случае является неполным частным.
Чтобы получить остаток, нужно из 17 вычесть произведение 3 и 5, то есть 17 – 3*5 = 2. Остаток – 2.
Как найти частное чисел
Пришли в цирк трое ребят: Вася, Коля и Оля. На входе их встречал клоун Бим, который дарил детям шарики. У него в руках было 6 шариков, но дарил он их за отгадки. Клоун спросил у ребят:
— Мне надо подарить вам шарики, какое математическое действие я буду применять?
— Деление! — быстро ответил Коля. — Ты же будешь делить шарики между нами.
Клоун хитро прищурился:
— А как называются члены деления?
— Мы недавно это изучали! — воскликнула Оля. — Всё количество шариков, которое ты будешь делить, называется делимое. У тебя сейчас 6 шариков, значит здесь делимое — 6!
— А то, на сколько ребят ты их разделишь, называется делитель, — вмешался Вася. — Нас трое ребят, значит делитель — 3!
Коля продолжил:
— У каждого из нас будет часть шариков, и результат от деления называется частным.
— Какое же здесь будет частное? — спрашивает Бим.
— Два! — не сговариваясь, хором ответили ребята.
— Правильно, каждому из вас достанется по два шарика, это и есть частное.
Ребята ответили на все вопросы Бима, и каждый получил по два шарика — как результат деления:
6 (делимое) : 3 (делитель) = 2 (частное).
Запишем цифрами:
6:3=2
| Делимое | Делитель | Частное |
| 6 | 3 | 2 |
В этом выражении 6 (делимое) стоит самым первым, 3 (делитель) — на втором месте. А частное (2) — после знака равенства справа.
Итак, частное — это число, которое получается в результате деления делимого на делитель.
Проверка деления умножением
— Я что-то не пойму. Это уже умножение, а не деление! — говорит Бим. — Выходит, что деление — действие обратное умножению. То есть, мы можем проверить деление умножением?
— Да, — ответил Бом.
Деление — действие, обратное умножению. Для того чтобы проверить деление, надо провести умножение.
Центр образовательных технологий Advance
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:

Приведём пример:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
(12∗3) /2 = 6∗3 — увеличили делимое на 3, равенство верное: 36 / 2 = 18;
(12 / 3) / 2 = 6 / 3 — уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Нахождение значения частного чисел
Пример:
12 : 3 = 4 (в числе 12 4 раза содержится по 3)
15 : 5 = 3 (в числе 15 5 раз содержится по 5)
Нужно знать, что правильность определения частного от деления числа всегда можно проверить путем перемножения его на делитель, либо делимое поделить на частное и получить делитель.
Например:
20 : 4 = 5
Перемножим частное двух чисел на делитель и получим делимое:
4 * 5 = 20
Разделим делимое на частное и получим делитель:
20 : 5 = 4
Таким образом, мы доказали правильность определения частного.
Деление с остатком
Деление с остатком есть отыскание наибольшего целого числа, которое в произведении с делителем дает число, не превышающее делимое. Искомое число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком. Он всегда меньше делителя.
19 не делится нацело на 5.Числа 1, 2, 3 в произведение с 5 дают 5, 10, 15,не превосходящие делимое 19,но уже 4 дает в произведении с 5 число 20, большее, чем 19.Поэтому неполное частное есть 3.Разность между 19 и произведением 3 · 5 = 15 есть 19 — 15 = 4;поэтому остаток есть 4.
Теги
паровоз (комментарий)- даже я знаю!
25 Апр, 20
давайте думать так.
у нас первый и второй вариант явно подходят к ответу, но какой из них выбрать?
приведём к общему знаменателю 2 вариант и первый.
5/127 и 3/7 12 для того что-бы определить ответ сравниваем числители(знаменатели можно не писать-для сравнения они нам не нужны)
5*7 =35
3*12 =36
35<36
значит выбираем первый вариант.
Значение частного двух чисел в математике
Содержание:
- Что такое частное чисел
-
Деление как операция
- Основные свойства деления
- Неполное частное
- Изменение частного в зависимости от изменения делимого и делителя
-
Задачи, примеры вычисления частного
- Задача 1
- Задача 2
Что такое частное чисел
Частное чисел – это результат деления одного числа на другое. Оно показывает, сколько раз число a содержится в числе b.
Деление как операция
Деление – арифметическая операция, обратная умножению, суть которой заключается в нахождении одного из сомножителей по произведению и другому множителю. В данном случае произведение переходит в делимое, имеющийся сомножитель – в делитель, искомый сомножитель – в частное.
Подобно тому, как неоднократно прибавить число – это значит умножить, так и неоднократно вычесть – это значит разделить.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На письме данную операцию можно обозначать разными символами:
- : двоеточием;
- ÷ обелюсом;
- / косой чертой (слеш);
- — горизонтальной чертой (знак дроби).
Процесс деления имеет следующий вид:
(frac{делимое}{делитель}=частное)
В цифрах данное выражение можно записать так:
(15 : 5 = 3,)
(15 ÷ 5 = 3,)
(15/5 = 3,)
(frac{15}{5}=3.)
Основные свойства деления
Деление не коммутативно, то есть не перестановочно – от перемены мест элементов операции частное изменяется:
(a : b ≠ b : a;)
Деление не ассоциативно – то есть при последовательном выполнении деления трех или более чисел последовательность операций имеет значение, при смене порядка выполнения изменится результат:
((a : b):c ≠ a : (b : c);)
Деление дистрибутивно справа – на одном и том же множестве две бинарные операции имеют свойство согласованности:
((a + b): x = (a : x)+(b : x);)
Имеется единственный нейтральный элемент – число 1, при делении на единицу результатом является исходное число (делимое):
(а : 1 = а;)
Имеется единственный обратный элемент – число 1, при делении единицы на число результатом является число, обратное исходному (делителю):
(1 : а = а^-1, а ≠ 0;)
Существует единственный нулевой элемент – число 0, при делении нуля на любое число результатом будет нуль:
(0 : а = 0, а ≠ 0;)
Деление на нулевой элемент не определено:
(а : 0 = ∞, а ≠ 0;)
Деление на противоположный элемент дает минус единицу:
(а : (-а) = -1.)
Неполное частное
Неполное частное – результат, который получился после деления с остатком.
Под делением с остатком понимается нахождение наибольшего целого числа, которое в произведении с делителем дает число, не превышающее делимое. Это искомое и называют неполным частным.
Разность между делимым и произведением делителя на неполное частное называется остатком, который всегда меньше делителя.
Например, 17 не делится без остатка на 5.
Наибольшее число, результат умножения которого на 5 не превосходит 17, это 3. 3 в данном случае является неполным частным.
Чтобы получить остаток, нужно из 17 вычесть произведение 3 и 5, то есть 17 – 3*5 = 2. Остаток – 2.
Изменение частного в зависимости от изменения делимого и делителя
Изменение делимого:
- увеличение делимого в несколько раз приведет к тому, что частное увеличится во столько же раз:
((а * x) : b = c * x;)
- уменьшение делимого в несколько раз приведет к тому, что частное уменьшится во столько же раз:
((a : x) : b = c : x.)
Изменение делителя:
- увеличение делителя в несколько раз приведет к тому, что частное уменьшится во столько же раз:
(а : (b * x) = c : x;)
- уменьшение делителя в несколько раз приведет к тому, что частное увеличится во столько же раз:
(а : (b : x) = c * x.)
Частное не изменится, если делимое и делить одновременно увеличить или уменьшить в одинаковое количество раз:
((а * x) : (b * x) = c;)
((а : x) : (b : x) = c;)
Задачи, примеры вычисления частного
Для того, чтобы проиллюстрировать данную арифметическую операцию, решим простые задачи.
Задача 1
В книге 891 страница. Она поделена на 9 равных глав. Узнайте, сколько страниц в одной главе.
Решение:
Для этого количество страниц разделим на количество глав:
891 : 9 = 99 (страниц)
Ответ: 99 страниц.
Задача 2
У Антона есть 22 апельсина. Он хочет приготовить из них компот. Для одного литра компота ему понадобится 3 апельсина. Нужно вычислить, сколько литров напитка сможет приготовить Антон и сколько апельсинов у него останется.
Решение:
22 : 3 = 7 (литров) (остаток 1)
Ответ: 7 литров, 1 апельсин останется.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Частное чисел в математике: что это такое? В школе учат действие деление, где есть делимое, делитель и частное. Что означают эти названия? Давайте разбираться!
Содержание статьи:
Частное чисел в математике: что это такое
Однажды клоун Бим решил выучить математическое действие деление и нашел для себя в интернете вот такое определение:
Определение. Говорят, что a делится на b, если существует натуральное число с, при умножении которого на b получается а: a=b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
Как мне это понять? — задумался Бим. — Но скоро представление, пойду ребят к нам приглашать.
Как найти частное чисел
Пришли в цирк трое ребят: Вася, Коля и Оля. На входе их встречал клоун Бим, который дарил детям шарики. У него в руках было 6 шариков, но дарил он их за отгадки. Клоун спросил у ребят:
— Мне надо подарить вам шарики, какое математическое действие я буду применять?
— Деление! — быстро ответил Коля. — Ты же будешь делить шарики между нами.
Клоун хитро прищурился:
— А как называются члены деления?
— Мы недавно это изучали! — воскликнула Оля. — Всё количество шариков, которое ты будешь делить, называется делимое. У тебя сейчас 6 шариков, значит здесь делимое — 6!
— А то, на сколько ребят ты их разделишь, называется делитель, — вмешался Вася. — Нас трое ребят, значит делитель — 3!
Коля продолжил:
— У каждого из нас будет часть шариков, и результат от деления называется частным.
— Какое же здесь будет частное? — спрашивает Бим.
— Два! — не сговариваясь, хором ответили ребята.
— Правильно, каждому из вас достанется по два шарика, это и есть частное.
Ребята ответили на все вопросы Бима, и каждый получил по два шарика — как результат деления:
6 (делимое) : 3 (делитель) = 2 (частное).
Запишем цифрами:
6:3=2
В этом выражении 6 (делимое) стоит самым первым, 3 (делитель) — на втором месте. А частное (2) — после знака равенства справа.
Итак, частное — это число, которое получается в результате деления делимого на делитель.
Полное и неполное частное
А потом было замечательное представление.
В антракте дети пошли в буфет. На подносе лежало семь пирожных. Как же их разделить поровну на трёх ребят?
Друзья задумались и взяли по 2 пирожных, а последним, которое было в остатке, угостили клоуна Бима.
— Теперь я понял! — воскликнул Бим. — Если нельзя всё число пирожных поделить между ребятами без остатка, то такой результат от деления называется неполным частным. А то, что осталось после деления, так и называется остатком и записывается это вот так:
7:3=2(1)
Здесь 7 (делимое) по-прежнему стоит в начале выражения, 3 (делитель) — в середине, 2 (неполное частное) — справа. Но после неполного частного ещё пишем в скобках остаток (1).
- Полное частное — результат деления, когда делимое делится нацело на делитель (остаток равен 0, его и писать незачем).
- Неполное частное — это результат деления с остатком (когда делимое не делится нацело на делитель).
Как найти делитель
Когда дети ушли занимать свои места, буфетчица подошла к Биму и спросила:
— Я забыла, сколько было ребят. Помню только, что каждый из них съел по два пирожных, а всего им досталось 6 штук. Сколько же посетителей было у меня?
Тут в буфет заглянул дрессировщик Бом и быстренько решил эту задачку. Он разделил 6 (делимое) на 2 (частное) и получил 3 (делитель).
— Всего было трое ребят, — ответил Бом.
— Верно! — вспомнил Бим.
Для того чтобы найти делитель, надо делимое разделить на частное.
6:2=3
Здесь 6 – делимое, 2 – частное, а 3 – делитель.
Как найти делимое
— А сколько ты подарил всего шариков трём ребятам? — спросил Бом.
— Забыл, — ответил Бим. — Помню только, что детей было трое, и каждому досталось по два шарика.
Бом и говорит:
— Тогда надо 3 (делитель) умножить на 2 (частное), получится 6.
Для того чтобы найти делимое, надо делитель умножить на частное.
Запишем это цифрами:
3*2=6.
3 — наш делитель, 2 — частное, а 6 — делимое.
Проверка деления умножением
— Я что-то не пойму. Это уже умножение, а не деление! — говорит Бим. — Выходит, что деление — действие обратное умножению. То есть, мы можем проверить деление умножением?
— Да, — ответил Бом.
Деление — действие, обратное умножению. Для того чтобы проверить деление, надо провести умножение.
Заключение
А клоун для себя сделал плакаты и теперь каждый день может сразу вспомнить, что:
Определение. Говорят, что а делится на b, если существует число с, при умножении которого на b получается а: a= b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
- Деление — действие, обратное умножению;
- умножение проверяет правильность математического действия — деления;
- для того чтобы найти делимое, надо делитель умножить на частное;
- для того чтобы найти делитель, надо делимое разделить на частное.
Итак, теперь мы знаем, что же такое частное в математике. Оказывается, оно бывает полным и неполным! Кроме того, нетрудно будет найти делитель, делимое и проверить деление умножением. И если учитель спросит в школе: «Частное чисел в математике: что это такое?» — сможем ответить сразу. И пусть любой пример или задача на эту тему будет вам по плечу!
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
10 : 2 = 5.
Частное чисел – это итог процесса деления одного значения на второе. Пример:
28 : 7 = 4,
где 28 — делимое;
7 — делитель;
4 — частное.
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
Приведём пример:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
(12∗3) /2 = 6∗3 – увеличили делимое на 3, равенство верное: 36 / 2 = 18;
(12 / 3) / 2 = 6 / 3 – уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
54 / (6∗3) = 9 / 3 – увеличили делитель в 3 раза, равенство верное: 54 / 18 =3;
54 / (6 / 3) = 9∗3 – уменьшили делитель в 3 раза, получаем равенство: 54 / 2 = 27.
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.