Как найти наименьшее число среди положительных

Как найти наименьшее число среди положительных

Часто случается, что в одном диапазоне ячеек находятся вместе положительные и отрицательные числа. Необходимо определить экстремальные значения, но с определенными условиями. Следует получить наименьшее значение для положительных чисел и отдельно для отрицательных. Для решения данной задачи не достаточно просто использовать функции =МИН(), =МАКС() или =НАИМЕНЬШИЙ(), =НАИБОЛЬШИЙ(). Иначе при обращении функций к диапазону с перемешанными положительными и отрицательными числами, будет возвращено только отрицательное наименьшее значение. Поэтому следует использовать специальную формулу с функциями.

Наименьшее положительное число

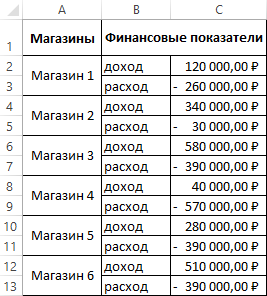
Допустим у нас есть статистика доходов и расходов сети магазинов за месяц. А нам нужно узнать какие из торговых точек наименее затратные по расходам и наименее прибыльны по доходам. Для презентации решения будем использовать пример таблицы с доходами и расходами магазинов как показано на рисунке:

Доходы и расходы.

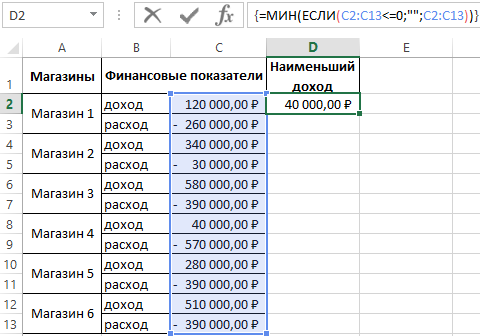
В первую очередь следует найти наименьший доход. Для этого формула должна сначала рассмотреть группу, состоящую только из положительных. После чего найдите наименьшее положительное значение функции. Для этого:

  1. В ячейке D2 введем следующую формулу:
  2. После ввода формулы для подтверждения необходимо нажать комбинацию горячих клавиш: CTRL+SHIFT+Enter, так как она должна выполняться в массиве. Если все сделано правильно тогда в строке формул будут видны фигурные скобки.

Минимальный доход.

Разбор принципа действия формулы для поиска наименьшего положительного числа:

Логическая функция =ЕСЛИ(), которая выполняется в массиве формул, проверяет каждую ячейку диапазона C2:C13 какая из них содержит число меньше чем 0 или равно нулю (<=0). Таким образом создается условная таблица в памяти с логическими значениями:

  • ЛОЖЬ – для положительных чисел (в данном случаи и для нуля);
  • ИСТИНА – для отрицательных чисел.

После чего в условной таблице функция ЕСЛИ заменяет все значения ИСТИНА на пустые (””). А вместо значения ЛОЖЬ подставляются те числа положительные, которые и были раньше в диапазоне C2:C13. И завершает вычисления формулы функция =МИН(), которая из условной таблицы (уже отфильтрованной от отрицательных значений и нулей) возвращает нам наименьшее положительное число.



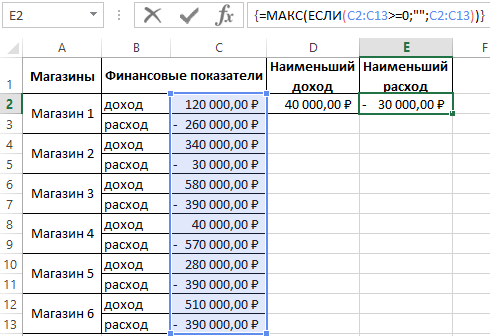
Наибольшее отрицательное число в диапазоне ячеек

Чтобы найти наименьшие расходы среди отрицательных значений укажите наибольшее. Для этого следует выполнить следующие действия:

  1. В ячейке E2 введите формулу:
  2. Так же, как и предыдущей формуле после ввода необходимо нажать комбинацию клавиш: CTRL+SHIFT+Enter, так как она должна выполняться в массиве. Если все сделано правильно в строке формул появятся фигурные скобки.

Минимальный расход.

Скачать формулы для поиска наименьшего положительного и наибольшего отрицательного числа

В результате мы быстро и легко переделили самый слабый магазин по доходам – это №4. А наименее затратная торговая точка по расходам – это магазин №2.

Источник

Задача 3.20. Поступает последовательность из N вещественных чисел. Определить наибольший элемент последовательности.

Входные данные: N — целое число; X — вещественное число, определяет текущий элемент последовательности.

Выходные данные: Max — вещественное число, элемент последовательности с наибольшим значением.

Промежуточные переменные: i — параметр цикла, номер вводимого элемента последовательности.

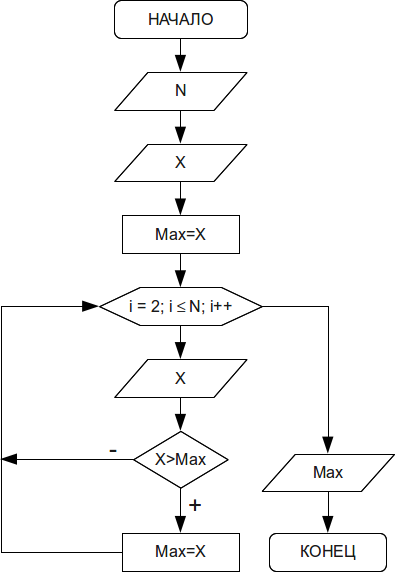
Алгоритм поиска наибольшего элемента в последовательности следующий (рис. 3.31). Вводится N — количество элементов последовательности и X — первый элемент последовательности. В памяти компьютера отводится ячейка, например с именем Max, в которой будет храниться наибольший элемент последовательности — максимум. Далее предполагаем, что первый элемент последовательности наибольший и записываем его в Max. Затем вводим второй элемент последовательности и сравниваем его с предполагаемым максимумом. Если окажется, что второй элемент больше, его записывают в ячейку Max. В противном случае никаких действий не предпринимаем. Потом переходим к вводу следующего элемента последовательности (X), и алгоритм повторяется с начала. В результате в ячейке Max сохранится элемент последовательности с наибольшим значением9Для поиска наименьшего элемента последовательности (минимума), предполагают, что первый элемент — наименьший, записывают его в ячейку min, а затем среди элементов после-довательности ищут число, значение которого будет меньше чем предполагаемый минимум..

Алгоритм поиска наибольшего числа в последовательности.

Рис.
3.31.
Алгоритм поиска наибольшего числа в последовательности.

Текст программы на С++:

#include <iostream>
using namespace std;
int main ( )
{
	unsigned int i,N;
	float X,Max;
	cout<<" N = "; cin>>N;
	cout<<" X = "; cin>>X; //Ввод первого элемента последовательности
	//Параметр цикла принимает стартовое значение i =2, т.к. первый элемент
	//уже введён предположим, что он максимальный, т.е. Max=X.
	for ( i =2, Max=X; i<=N; i++)
	{
	cout<<" X = "; cin>>X; //Ввод следующих элементов последовательности.
	//Если найдётся элемент, превышающий максимум, записать его в ячейку Max,
	//теперь он предполагаемый максимум.
	if (X>Max) Max=X;
	}
	//Вывод наибольшего элемента последовательности.
	cout<<" Max = "<<Max<<" n ";
	return 0;
}

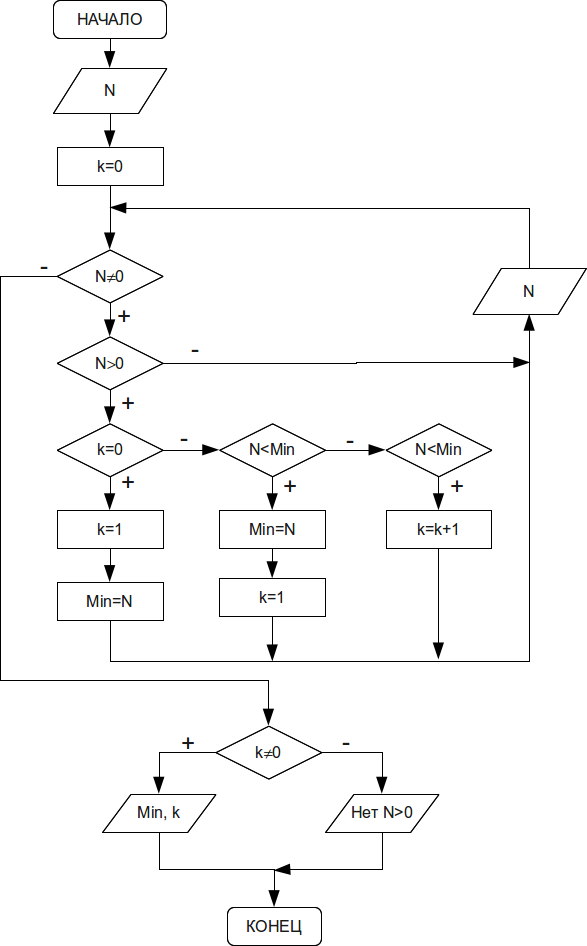
Задача 3.21. Вводится последовательность целых чисел, 0 — конец последовательности. Найти наименьшее число среди положительных, если таких значений несколько10Предположим вводится последовательность чисел 11, -3, 5, 12, -7, 5, 8,-9, 7, -6, 10, 5, 0. Наименьшим положительным числом является 5. Таких минимумов в последовательности 3., определить, сколько их.

Блок-схема решения задачи приведена на рис. 3.32.

Алгоритм поиска минимального положительного числа в последовательности.

Рис.
3.32.
Алгоритм поиска минимального положительного числа в последовательности.

Далее приведён текст подпрограммы с подробными комментариями11Алгоритм поиска максимального (минимального) элементов последовательности подробно описан в задаче 3.20.

#include <iostream>
using namespace std;
int main ( )
{
	float N, Min; int K;
	//Предположим, что в последовательности нет положительных чисел, K=0.
	//Вводим число и если оно не равно нулю
	for ( cout<<" N = ", cin>>N,K=0;N!=0; cout<<" N = ", cin>>N)
	//проверяем является ли оно положительным.
	if (N>0)
	//если K=0, поступил 1-й положительный элемент, предположим, что он минимальный.
	if (K==0) {K=1;Min=N; }
	//если элемент не первый, сравниваем его с предполагаемым минимумом,
	//если элемент меньше, записываем его в Min и сбрасываем счётчик
	else if (N<Min) {Min=N;K=1;}
	//если элемент равен минимуму, увеличиваем значение счётчика.
	else if (N==Min) K++; //Конец цикла
	//Если значение счётчика не равно нулю, печатаем значение
	//минимального элемента и количество таких элементов.
	if (K!=0) cout<<" Min = "<<Min<<" n "<<" K = "<<K<<" n ";
	//в противном случае выдаём сообщаем.
	else cout<<"В последовательности нет положительных элементов n ";
	return 0;
}
Источник

Принцип поиска максимального или
минимального элемента массива заключается
в следующем: в дополнительную переменную
заносится значение первого элемента
массива, которое принимается за максимум
(минимум); затем организовывается перебор
оставшихся элементов массива, каждый
из которых сравнивается с максимумом
(минимумом); если текущий элемент массива
оказывается больше (меньше), чем принятый
за максимум (минимум), то этот элемент
становится максимальным (минимальным).
Таким образом, после завершения перебора
элементов массива в дополнительной
переменной окажется максимальное
(минимальное) значение среди элементов
массива. Фрагмент блок-схемы алгоритма,
реализующий описанный метод приведен
на рисунке 5.2.1.

В блоке 1 дополнительным переменным maxиmin, в которых
будут храниться максимальное и минимальное
значения соответственно, присваивается
значение 1-го элемента массива. Кроме
этого введены еще две переменныеimaxиimin, которые будут
использоваться для хранения номеров
максимального и минимального элементов
массива. С помощью блока модификации
(блок 2) организовывается цикл по перебору
элементов массива Х (перебор начинается
со 2-го элемента, так как 1-й элемент уже
обработан в блоке 1). Если текущий элемент
массиваXiбольше значения, которое хранится в
переменнойmax(блок 3), то за максимум принимается
значение этого элемента:max=Xi,
и запоминается его номер:imax=i(блок 4). Если текущий элемент массива
не больше максимума, то проверяется, не
меньше ли он минимума (блок 5). В случае
если текущий элементXiокажется меньше минимального значения,
которое хранится в переменнойmin,
то за минимум принимается значение
этого элемента:min=Xi,
и запоминается его номер:imin=i(блок 6). После выхода из цикла будут
выведены значения максимального и
минимального элементов, а также их
номера в массиве (блок 7).

Приведенный
выше алгоритм имеет один недостаток –
в нем используется две лишние переменныеmaxиmin.
Зная индекс элемента массива всегда
можно получить его значение, поэтому
нет необходимости хранить максимальное
и минимальное значения в отдельных
переменных. Оптимальный алгоритм
приведен на рис. 5.2.2.

В блоке 1 дополнительным переменным
imaxиimin,
используемых для хранения номеров
максимального и минимального элемента,
присваивается значение 1. Таким образом,
за максимум и минимум принимается 1-й
элемент массива, само же значение этого
элемента нигде дополнительно не
сохраняется. Оставшиеся элементы массива
также перебираются, начиная со второго
(блок 2). При этом каждый элемент массиваXi
 сравнивается с
элементами, имеющими номер равныйimax(блок 3) иimin(блок
6), т.е. с элементами принятыми за максимум
(минимум). Если результат проверки
условий является истиной, то в переменныхimaxиiminсохраняются индексы новых максимального
(блок 4) и минимального (блок 6) элементов.
После выхода из цикла будут выведены
значения максимального и минимального
элементов, а также их номера в массиве
(блок 7).

Если в массиве имеется несколько
элементов равных по значению максимальному
(минимальному) элементу, то алгоритмы,
приведенные на рис 5.2.1 и 5.2.2, определят
позицию только первого такого элемента.
Например, чтобы найти количество
элементов массива равных максимальному
и позицию последнего такого элемента,
можно воспользоваться алгоритмом,
приведенным на рис. 5.2.3.

В начале алгоритма за максимум принимается
1-й элемент массива и вводится переменная
kдля подсчета
количества элементов равных максимальному
(блок 1). Затем организовывается цикл по
перебору оставшихся элементов массива
(блок 2). На каждом шаге цикла выполняется
следующая последовательность действий.

Вначале текущий элемент массива Xiсравнивается с максимальным (блок 3).
Если он оказывается больше элемента,
принятого за максимальный, то запоминается
номер этого элемента и переменнойkприсваивается 1 (блок 4). Это означает,
что встретился первый «новый» максимальный
элемент.

Если текущий элемент не больше максимума,
значит, он может быть равным или меньше
максимального элемента. Поэтому в блоке
5 текущий элемент массива Xi
проверяется на равенство
максимальному. Если он оказывается
равным максимуму, то опять запоминается
номер текущего элемента и значение
переменнойkувеличивается на 1 (блок 6). Это означает,
что встретился следующий элемент равный
максимальному элементу. В итоге после
выхода из цикла в переменнойimaxбудет храниться индекс последнего по
счету элемента равного максимальному,
а в переменнойkколичество элементов, равных максимуму.
Если же из блока 6 убрать операциюimax=i,
то в переменнойimax,
как и в предыдущих примерах будет
сохранен номер первого по счету элемента
равного максимальному.

В некоторых задачах невозможно вначале
принять за максимум (минимум) первый
элемент массива. Например, если элементы
массива ещё не определены (не введены
или не вычислены), или если необходимо
найти максимум (минимум) только среди
положительных, четных по значению и
т.д. элементов. Во втором случае неизвестно
когда в массиве встретится первый такой
элемент. В таких ситуациях можно
использовать способ, реализованный в
алгоритме из примера 5.2.

Пример 5.2.В массиве Х [N]
найти минимальный положительный элемент.

Массив
Х может содержать как положительные,
так и отрицательные элементы. Поэтому
неизвестно какой элемент массива или
произвольное значение можно принять
за начальный минимум. Решение поставленной
задачи можно разбить на два этапа: поиск
положительных элементов в массиве с
определением первого такого элемента
и поиск среди положительных элементов
минимального по значению. Блок-схема
алгоритма приведена на рис. 5.2.4.

В нашем примере нумерация элементов
массива начинается с единицы, поэтому
в качестве начального значения для
переменной iminпринимается 0 (блок 1), т.е. значение
которое не могут принимать индексы
элементов массива Х. Таким образом
показывается, что при обработке массива
еще не встречался положительный элемент,
который можно принять за начальное
значение для минимума. Затем организовывается
цикл по перебору всех элементов массива
(блок 2). На каждом шаге цикла выполняется
следующая последовательность действий.

В блоке 3 проверяется, не является ли
текущий элемент массива Xiположительным. Если он отрицательный
или равен нулю, то такой элемент
пропускается и над ним не выполняется
никаких действий. ЕслиXi> 0, то в блоке 4 проверяется, не является
ли этот элемент первым встретившимся
положительным элементом массива
(признаком чего служит значениеiminравное 0). В этом случае в блоке 5 переменнойiminбудет присвоено
текущее значениеi.
Таким образом, за начальное значение
для минимума будет принято значение
первого по счету положительного элемента
массива Х. Эта ситуация может возникнуть
только один раз, и при дальнейшей работе
цикла блок 5 больше выполняться не будет.
Остальные положительные элементы
массива в блоке 6 будут сравниваться с
элементом массива, принятым в текущий
момент за минимум. Если такой элемент
окажется меньше минимального, то в блоке
7 в переменнойiminбудет сохранен его номерi.

После выхода из цикла проверяется, не
равно ли значение iminнулю (блок 8), так как сразу же выводить
значение минимального элемента массиваXimin
и его номерimin(блок 9) нельзя. Это объясняется тем что,
если в массиве Х не будет положительных
элементов, то значение переменнойiminостанется равным нулю, а обращение к
несуществующему элементу массиваХ0не допустимо.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Добавить комментарий