Найдите наименьшее число х на отрезке [0; п], для которых sin(x), cos(2x)/ корень2, cos(x) являются тремя последовательными членами арифметической прогрессии.
школьная-математика
задан
10 Янв ’18 0:32
Викторрр
1●1
Среднее число должно быть полусуммой крайних. cos x+sin x=cos2x=(cos x+sin x)(cos x-sin x). То есть cos x+sin x=0 или cos x – sin x=1. На отрезке [0,п] наименьшим будет число x=0, что в принципе видно сразу. Но в таком виде задача сильно упрощается. Если же говорить о наименьшем положительном, то это будет x=3п/4.
(10 Янв ’18 0:41)
falcao
10|600
символов нужно
символов осталось
Загрузить PDF
Загрузить PDF
Из этой статьи вы узнаете, как найти число членов арифметической прогрессии. Это не так сложно, как кажется.
-
1
Выясните разность прогрессии. Скорее всего, она будет дана; если нет, будут даны два последовательных члена прогрессии. Обозначим разность как d.[1]
-
2
Запишите первый и последний член прогрессии. Эти члены понадобятся, чтобы найти общее число членов прогрессии. Например, первый член обозначим как A, а последний как L.[2]
-
3
Найдите число членов прогрессии. Если число членов обозначить как n, формула запишется так:
n = (L-A)/d + 1
. То есть разделите разность между последним (L) и первым (А) членами на разность прогрессии (d), а затем к результату прибавьте 1.[3]
Реклама
Советы
- Разность между последним и первым членами прогрессии всегда делится на разность прогрессии.
Реклама
Предупреждения
- Не перепутайте разность между последним и первым членами прогрессии с разностью прогрессии.
Реклама
Об этой статье
Эту страницу просматривали 26 091 раз.
Была ли эта статья полезной?
Содержание
- Наименьшее общее кратное
- Общее кратное
- Наименьшее общее кратное
- Как найти НОК
- С помощью разложения на простые множители
- Нахождение НОК через НОД
- Калькулятор НОК
- Как найти наименьшее натуральное число
- Как найти НОК
- Первый способ нахождения НОК
- Второй способ нахождения НОК
- Особые случаи нахождения НОК
- Нахождение путём разложения на множители
- Нахождение путём подбора
- Нахождение путём последовательного нахождения НОК
- Содержание статьи
- Нахождение наименьшего общего кратного: основные понятия
- Как найти наименьшее общее кратное чисел
Наименьшее общее кратное
Общее кратное
Число может быть кратно не одному, а сразу нескольким числам, такое число называется общим кратным данных чисел.
Числу 3 кратны числа: 6, 9, 12, 15 и т. д.
Числу 4 кратны числа: 8, 12, 16, 20 и т. д.
Можно заметить, что одно и тоже число (12) делится нацело сразу на оба числа 3 и 4. Следовательно, число 12 есть общее кратное чисел 3 и 4.
Общее кратное чисел — это любое число, которое делится без остатка на каждое из данных чисел.
Найти общее кратное нескольких натуральных чисел достаточно легко, можно просто перемножить данные числа, полученное произведение и будет их общим кратным.
Пример. Найти общее кратное для чисел 2, 3, 4, 6.
2 · 3 · 4 · 6 = 144.
Число 144 — общее кратное чисел 2, 3, 4 и 6.
Для любого количества натуральных чисел существует бесконечно много кратных.
Пример. Для чисел 12 и 20 кратными будут числа: 60, 120, 180, 240 и т. д. Все они являются общими кратными для чисел 12 и 20.
Наименьшее общее кратное
Наименьшее общее кратное (НОК) нескольких чисел — это самое маленькое натуральное число, которое делится без остатка на каждое из этих чисел.
Пример. Наименьшим общим кратным чисел 3, 4 и 9 является число 36, никакое другое число меньше 36 не делится одновременно на 3, 4 и 9 без остатка.
Наименьшее общее кратное записывается так:
Числа в круглых скобках могут быть указаны в любом порядке.
Пример. Запишем наименьшее общее кратное чисел 3, 4 и 9:
Как найти НОК
Рассмотрим два способа нахождения наименьшего общего кратного: с помощью разложения чисел на простые множители и нахождение НОК через НОД.
С помощью разложения на простые множители
Чтобы найти НОК нескольких натуральных чисел, надо разложить эти числа на простые множители, затем взять из этих разложений каждый простой множитель с наибольшим показателем степени и перемножить эти множители между собой.
Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.
Решение: разложим каждое из этих чисел на простые множители:
99 = 3 · 3 · 11 = 3 2 · 11 ,
54 = 2 · 3 · 3 · 3 = 2 · 3 3 .
Наименьшее общее кратное должно делиться на 99, значит, в его состав должны входить все множители числа 99. Далее НОК должно делиться и на 54, т. е. в его состав должны входить множители и этого числа.
Выпишем из этих разложений каждый простой множитель с наибольшим показателем степени и перемножим эти множители между собой. Получим следующее произведение:
2 · 3 3 · 11 = 594.
Это и есть наименьшее общее кратное данных чисел. Никакое другое число меньше 594 не делится нацело на 99 и 54.
Ответ: НОК (99, 54) = 594.
Так как взаимно простые числа не имеют одинаковых простых множителей, то их наименьшее общее кратное равно произведению этих чисел.
Пример. Найдите наименьшее общее кратное двух чисел 12 и 49.
Решение: разложим каждое из этих чисел на простые множители:
12 = 2 · 2 · 3 = 2 2 · 3,
Применяя к этому случаю правило, мы придём к заключению, что взаимно простые числа надо просто перемножить:
2 2 · 3 · 7 2 = 12 · 49 = 980.
Ответ: НОК (12, 49) = 980.
Таким же образом надо поступать, когда нужно найти наименьшее общее кратное простых чисел.
Пример. Найдите наименьшее общее кратное чисел 5, 7 и 13.
Решение: так как данные числа являются простыми, то просто перемножим их:
Ответ: НОК (5, 7, 13) = 455.
Если большее из данных чисел делится на все остальные числа, то это число и будет наименьшим общим кратным данных чисел.
Пример. Найдите наименьшее общее кратное чисел 24, 12 и 4.
Решение: разложим каждое из этих чисел на простые множители:
24 = 2 · 2 · 2 · 3 = 2 3 · 3,
12 = 2 · 2 · 3 = 2 2 · 3,
Можно заметить, что разложение большего числа содержит все множители остальных чисел, значит большее из этих чисел делится на все остальные числа (в том числе и само на себя) и является наименьшим общим кратным:
Ответ: НОК (24, 12, 4) = 24.
Нахождение НОК через НОД
НОК двух натуральных чисел равно произведению этих чисел, поделённого на их НОД.
Правило в общем виде:
Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.
Теперь мы можем вычислить НОК этих чисел по формуле:
НОК (99, 54) = 99 · 54 : НОД (99, 54) = 5346 : 9 = 594.
Ответ: НОК (99, 54) = 594.
Чтобы найти НОК трёх или более чисел используется следующий порядок действий:
- Находят НОК любых двух из данных чисел.
- Затем находят наименьшее общее кратное найденного НОК и третьего числа и т. д.
- Таким образом поиск НОК продолжается до тех пор, пока есть числа.
Пример. Найдите наименьшее общее кратное чисел 8, 12 и 9.
Решение: сначала находим наибольший общий делитель любых двух из этих чисел, например, 12 и 8:
Вычисляем их НОК по формуле:
НОК (12, 8) = 12 · 8 : НОД (12, 8) = 96 : 4 = 24.
Теперь найдём НОК числа 24 и оставшегося числа 9. Их НОД:
Вычисляем НОК по формуле:
НОК (24, 9) = 24 · 9 : НОД (24, 9) = 216 : 3 = 72.
Ответ: НОК (8, 12, 9) = 72.
Калькулятор НОК
Данный калькулятор поможет вам найти наименьшее общее кратное чисел. Просто введите числа через пробел или запятую и нажмите кнопку Вычислить НОК .
Источник
Как найти наименьшее натуральное число
Для того, чтобы находить общий знаменатель при сложении и вычитании дробей с разными знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).
Кратное числу « a » — это число, которое само делится на число « a » без остатка.
Числа кратные 8 (то есть, эти числа разделятся на 8 без остатка): это числа 16, 24, 32 …
Кратные 9: 18, 27, 36, 45 …
Чисел, кратных данному числу a бесконечно много, в отличии от делителей этого же числа. Делителей — конечное количество.
Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.
Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.
Как найти НОК
НОК можно найти и записать двумя способами.
Первый способ нахождения НОК
Данный способ обычно применяется для небольших чисел.
- Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
- Кратное числа « a » обозначаем большой буквой «К».
Пример. Найти НОК 6 и 8 .
Второй способ нахождения НОК
Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.
- Разложить данные числа на простые множители. Подробнее правила разложения на простые множители вы можете прочитать в теме как найти наибольший общий делитель (НОД).
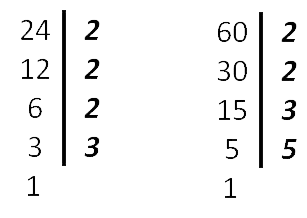
- Выписать в строчку множители, входящие в разложение самого большого из чисел, а под ним — разложение остальных чисел.
Количество одинаковых множителей в разложениях чисел может быть разное.
НОК (24, 60) = 2 · 2 · 3 · 5 · 2
Ответ: НОК (24, 60) = 120
Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24) .
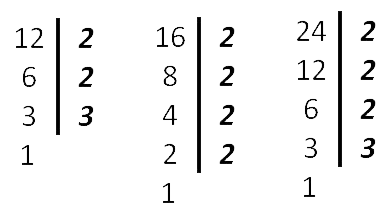24 = 2 · 2 · 2 · 3
Как видим из разложения чисел, все множители 12 вошли в разложение 24 (самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из разложения числа 16 .
НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48
Ответ: НОК (12, 16, 24) = 48
Особые случаи нахождения НОК
- Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.
Например, НОК (60, 15) = 60
Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее кратное равно произведению этих чисел.
На нашем сайте вы также можете с помощью специального калькулятора найти наименьшее общее кратное онлайн, чтобы проверить свои вычисления.
Рассмотрим три способа нахождения наименьшего общего кратного.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наименьшего общего кратного путём разложения данных чисел на простые множители.
Допустим, нам требуется найти НОК чисел: 99, 30 и 28. Для этого разложим каждое из этих чисел на простые множители:
Чтобы искомое число делилось на 99, на 30 и на 28, необходимо и достаточно, чтобы в него входили все простые множители этих делителей. Для этого нам необходимо взять все простые множители этих чисел в наибольшей встречающейся степени и перемножить их между собой:
2 2 · 3 2 · 5 · 7 · 11 = 13 860
Таким образом, НОК (99, 30, 28) = 13 860. Никакое другое число меньше 13 860 не делится нацело на 99, на 30 и на 28.
Чтобы найти наименьшее общее кратное данных чисел, нужно разложить их на простые множители, затем взять каждый простой множитель с наибольшим показателем степени, с каким он встречается, и перемножить эти множители между собой.
Так как взаимно простые числа не имеют общих простых множителей, то их наименьшее общее кратное равно произведению этих чисел. Например, три числа: 20, 49 и 33 – взаимно простые. Поэтому
НОК (20, 49, 33) = 20 · 49 · 33 = 32 340.
Таким же образом надо поступать, когда отыскивается наименьшее общее кратное различных простых чисел. Например, НОК (3, 7, 11) = 3 · 7 · 11 = 231.
Нахождение путём подбора
Второй способ заключается в нахождении наименьшего общего кратного путём подбора.
Пример 1. Когда наибольшее из данных чисел делится нацело на другие данные числа, то НОК этих чисел равно большему из них. Например, дано четыре числа: 60, 30, 10 и 6. Каждое из них делится нацело на 60, следовательно:
НОК (60, 30, 10, 6) = 60
В остальных случаях, чтобы найти наименьшее общее кратное используется следующий порядок действий:
- Определяем наибольшее число из данных чисел.
- Далее находим числа, кратные наибольшему числу, умножая его на натуральные числа в порядке их возрастания и проверяя делятся ли на полученное произведение остальные данные числа.
Пример 2. Дано три числа 24, 3 и 18. Определяем самое большое из них – это число 24. Далее находим числа кратные 24, проверяя делится ли каждое из них на 18 и на 3:
24 · 1 = 24 – делится на 3, но не делится на 18.
24 · 2 = 48 – делится на 3, но не делится на 18.
24 · 3 = 72 – делится на 3 и на 18.
Таким образом, НОК (24, 3, 18) = 72.
Нахождение путём последовательного нахождения НОК
Третий способ заключается в нахождении наименьшего общего кратного путём последовательного нахождения НОК.
НОК двух данных чисел равно произведению этих чисел, поделённого на их наибольший общий делитель.
Пример 1. Найдём НОК двух данных чисел: 12 и 8. Определяем их наибольший общий делитель: НОД (12, 8) = 4. Перемножаем данные числа:
Делим произведение на их НОД:
Таким образом, НОК (12, 8) = 24.
Чтобы найти НОК трёх и более чисел используется следующий порядок действий:
- Сначала находят НОК каких-нибудь двух из данных чисел.
- Потом, НОК найденного наименьшего общего кратного и третьего данного числа.
- Затем, НОК полученного наименьшего общего кратного и четвёртого числа и т. д.
- Таким образом поиск НОК продолжается до тех пор, пока есть числа.
Пример 2. Найдём НОК трёх данных чисел: 12, 8 и 9. НОК чисел 12 и 8 мы уже нашли в предыдущем примере (это число 24). Осталось найти наименьшее общее кратное числа 24 и третьего данного числа – 9. Определяем их наибольший общий делитель: НОД (24, 9) = 3. Перемножаем НОК с числом 9:
Содержание статьи
- Как найти наименьшее общее кратное чисел
- Что такое взаимно простые числа
- Как разложить на множители числа
Нахождение наименьшего общего кратного: основные понятия
Чтобы понять, как вычислять НОК, следует определиться в первую очередь со значением термина «кратное».
Кратным числу А называют такое натуральное число, которое без остатка делится на А. Так, числами кратными 5 можно считать 15, 20, 25 и так далее.
Делителей конкретного числа может быть ограниченное количество, а вот кратных бесконечное множество.
Общее кратное натуральных чисел – это такое число, которое делится на них без остатка.
Как найти наименьшее общее кратное чисел
Наименьшее общее кратное (НОК) чисел (двух, трех или больше) – это самое маленькое натурально число, которое делится на все эти числа нацело.
Чтобы найти НОК, можно использовать несколько способов.
Для небольших чисел удобно выписать в строчку все кратные этих чисел до тех пор, пока среди них не найдется общее. Кратные обозначают в записи заглавной буквой К.
Например, кратные числа 4 можно записать так:
Так, можно увидеть, что наименьшим общим кратным чисел 4 и 6 является число 24. Эту запись выполняют следующим образом:
Если числа большие, или нужно найти наименьшее общее кратное трех и более чисел, то лучше использовать другой способ вычисления НОК.
Для выполнения задания необходимо разложить предложенные числа на простые множители.
Сначала нужно выписать в строчку разложение наибольшего из чисел, а под ним – остальных.
В разложении каждого числа может присутствовать различное количество множителей.
Например, разложим на простые множители числа 50 и 20.
В разложении меньшего числа следует подчеркнуть множители, которые отсутствуют в разложении первого самого большого числа, а затем их добавить к нему. В представленном примере не хватает двойки.
Теперь можно вычислить наименьшее общее кратное 20 и 50.
НОК (20, 50) = 2 * 5 * 5 * 2 = 100
Так, произведение простых множителей большего числа и множителей второго числа, которые не вошли в разложение большего, будет наименьшим общим кратным.
Чтобы найти НОК трех чисел и более, следует их все разложить на простые множители, как и в предыдущем случае.
В качестве примера можно найти наименьшее общее кратное чисел 16, 24, 36.
Так, в разложение большего числа на множители не вошли только две двойки из разложения шестнадцати (одна есть в разложении двадцати четырех).
Таким образом, их нужно добавить к разложению большего числа.
НОК (12, 16, 36) = 2 * 2 * 3 * 3 * 2 * 2 = 9
Существуют частные случаи определения наименьшего общего кратного. Так, если одно из чисел можно поделить без остатка на другое, то большее из этих чисел и будет наименьшим общим кратным.
Например, НОК двенадцати и двадцати четырех будет двадцать четыре.
Если необходимо найти наименьшее общее кратное взаимно простых чисел, не имеющих одинаковых делителей, то их НОК будет равняться их произведению.
Источник
