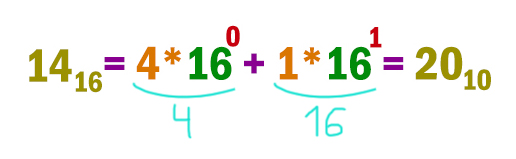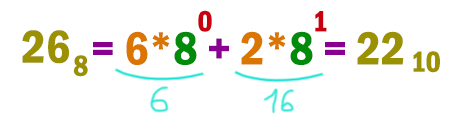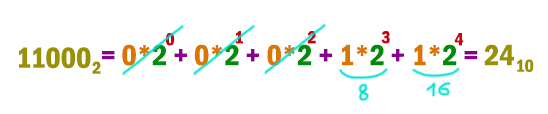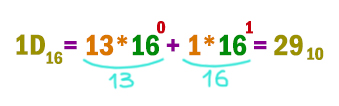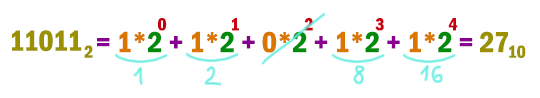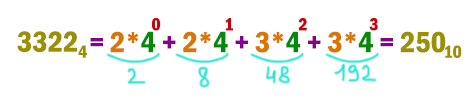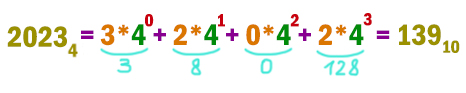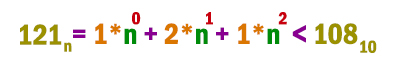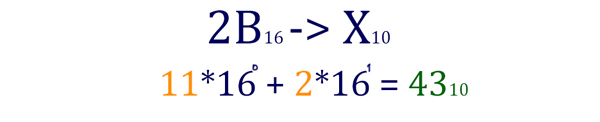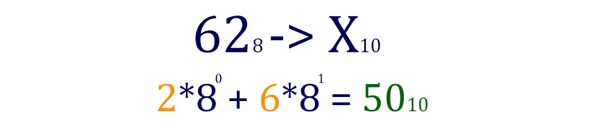Как найти наименьшее число в системе счисления

Формулировка задания: Укажите наименьшее основание системы счисления, в которой запись числа K-значна.

Задание входит в ЕГЭ по информатике для 11 класса под номером 16 (Кодирование чисел. Системы счисления).

Рассмотрим, как решаются подобные задания на примере.

Пример задания:

Укажите наименьшее основание системы счисления, в которой запись числа 70 трехзначна.

Решение:

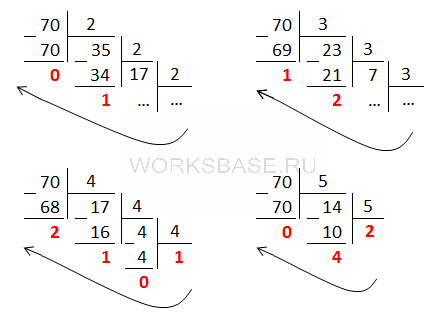
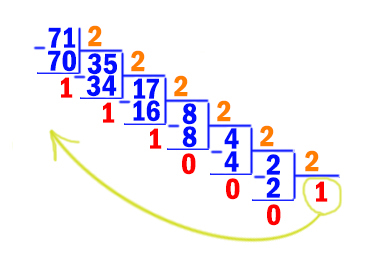
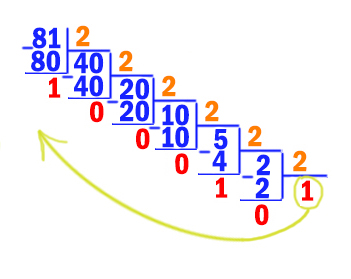
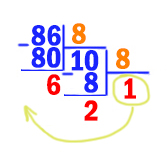
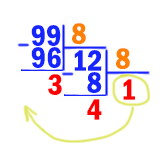
Решим задачу методом подбора: будем перебирать основания системы счисления, начиная с наименьшего (2), и переводить число 70 в каждую из этих систем счисления:

В двоичной, троичной и четвертичной системах счисления в числе больше 3 цифр. А в системе счисления с основанием 5 их ровно 3.

Таким образом, наименьшее основание системы счисления равно 5.

Ответ: 5

Поделитесь статьей с одноклассниками «Укажите наименьшее основание системы счисления, в которой запись – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.

Источник

The method to represent and work with numbers is known as number system. A number system is a system of writing to represent numbers. It is the mathematical notation used to represent numbers of a given set by using digits or other symbols. It allows us to operate arithmetic operations such as division, multiplication, addition, subtraction.

Some important number systems are as follows:

Decimal Number System
Binary Number System
Octal Number System
Hexadecimal Number System

Lets see about all these number systems in details.

Decimal Number System

The decimal number system consists of ten digits i.e. from 0 to 9. The base of decimal number system is 10. These digits can be used to represent or express any numeric value.

For example, the decimal number 153 consists of the digit 3 in ones place, the digit 5 in the tens place, and the digit 1 in hundreds place which can be represented as :

(1×10²) + (5×10¹) + (3×10⁰)

= (1 × 100) + (5 × 10) + (3 × 1) { where, 10⁰ = 1}

= 100 + 50 + 3

= 153

Binary Number System

The binary number system consists of only two digits i.e. 0 and 1. The base of the binary number system is 2. The digital computer represents all kinds of data in a binary number system.

For example, convert 100112 into a decimal number system.

(100111)₂ = 1 × 2⁵ + 0 × 2⁴ + 0 × 2³ + 1 × 2² + 1 × 2¹ + 1 × 2⁰

= 32 + 0 + 0 + 4 + 2 + 1

= (39)₁₀

Octal Number System

The octal number system consists of digits from 0 to 7. The base of the octal number system is 8. Octal number systems are basically used in computer applications.

For example, convert 1458 into decimal.

1458 = 1 × 8² + 4 × 8¹+ 5 × 8⁰

= 64 + 32 + 5

= 10110

Hexadecimal Number System

In the hexadecimal number system, numbers are first represented from digits 0 to 9 as decimal number system, and then the numbers are represented using alphabets from A to F. The base of the hexadecimal number system is 16.

For example, convert 26BC16 to decimal.

26BC16 = 2 × 16³ 6 × 16² + 11 × 16¹ + 12 × 16⁰

= 8192 + 1536 + 176 + 12

= 991610

What are the smallest and the largest six-digit numbers in the Number System?

Smallest six-digit number in the number system –

The smallest 6 digit number in the number system is 100000.

Explanation – If we subtract -1 from the number it becomes 5 digit number that is 99999 (five digit number). So 100000 is the smallest 6 digit number in the number system.

Smallest 6 digit number = 100000

=> 100000 – 1

=> 99999 (Which is 5 digit number)

So it is proved the 100000 is the smallest 6 digit number in the number system.

Largest six-digit number in the number system –

The largest 6 digit number in the number system is – 999999

Explanation – If you add 1 to this number it becomes 1000000 which is a 7 digit number. So 999999 is the largest six digit number in the number system.

Largest 6 digit number in the number system = 999999

= > 999999 + 1

= > 1000000 (which is 7 digit number)

Hence it is proved that 999999 is the largest six digit number.

Calculate how many number lie between these two values?

We can determine how many numbers lie between the smallest 6-digit number and the largest 6-digit number. We can simply do it by subtracting the smallest number from the largest number. That is –

⇒ 999999 − 100000 = 899999

Hence, total 899999 numbers are lie between the smallest 6-digit number and the largest 6-digit number.

123×5₁₅ + 1×233₁₅

примет вид:

12345₁₅+14233₁₅

Переводим числа в десятичную систему с помощью формулы в Экселе (берём окончательный вариант из комментария)

В десятичной системе исходное выражение записывается так:

58115+64623=122738

Вычисляем частное от деления результата исходного выражения на 14 , в десятичной системе:

122738/14=8767

Ответ:8767

автор вопроса выбрал этот ответ лучшим

Знаете ответ?

Смотрите также:

Какое из чисел 39, 75, 111011 наименьшее в десятичной системе счисления?

ЕГЭ Информатика, Как ответить на вопрос о восьмеричной системе счисления?

Зачем мне знания о системах счисления?

Какое из чисел 36, 65, 111010 наименьшее в десятичной системе счисления?

Где смотреть результаты ЕГЭ по информатике в 2023 году?

ОГЭ 2023 Информатика, Как найти максимальное число среди приведённых?

Какое из чисел 55, 124, 1010101 наименьшее в десятичной системе счисления?

Какое из чисел 46, 106, 1000101 наименьшее в десятичной системе счисления?

Какое из чисел 67, 150, 1101000 наименьшее в десятичной системе счисления?

Какое из чисел 81, 203, 1111111 наименьшее в десятичной системе счисления?

Источник

Привет! Сегодня исследуем 10 Задание из ОГЭ по информатике 2023.

Задание 9 из ОГЭ по информатике Вы можете научиться решать, прочитав статью по 13 заданию из ЕГЭ по информатике. Эту статью Вы можете найти здесь.

Десятое задание проверяет умение работать с различными системами счисления.

Задача (Классическая)

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

14₁₆, 26₈, 11000₂.

Решение:

Число 14 находится в шестнадцатеричной системе. Об этом говорит маленький индекс возле числа. Переведём его в нашу родную десятичную систему.

Берём поочередно цифры, начиная с младшего разряда. Первую правую цифру умножаем на 16 в нулевой степени, вторую цифру на 16 в первой степени и т.д. Умножаем на 16, потому что переводим из шестнадцатеричной системы. Степень потихоньку увеличивается на 1.

Необходимо помнить, что любое число в нулевой степени это единица!

Остаётся только посчитать полученный пример. Получается число 20 в десятичной системе.

Переведём число 26₈ из восьмеричной системы в нашу родную десятичную систему. Делаем аналогично предыдущему примеру.

Аналогично переведём число и из двоичной системы.

Наибольшее из трёх чисел это 24.

Ответ: 24

Задача (Классическая, закрепление)

1D₁₆, 36₈, 11011₂

Решение:

В шестнадцатеричной системе буквы при переводе в десятичную систему нужно превратить в числа.

A	B	C	D	E	F
10	11	12	13	14	15

Переведём первое число.

Переведём второе число.

Переведём третье число.

Наибольшее число получается 30.

Ответ: 30

Задача (Из десятичной в двоичную)

Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, в двоичной записи которого наименьшее количество единиц. В ответе запишите количество единиц в двоичной записи этого числа.

59₁₀, 71₁₀, 81₁₀

Решение:

Нужно каждое число перевести в двоичную систему счисления.

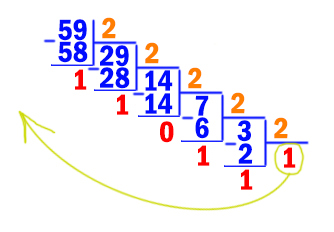
Переведём число 59₁₀ в двоичную систему.

Получается 59₁₀ = 111011₂. Здесь мы делим уголком на 2 (на основание системы, куда переводим) с остатком. Продолжаем делить, пока не получим 1. Затем остатки записываем задом наперёд. Получается число в двоичной системе счисления. Последнее число 1 (единицу) тоже берём.

Переведём число 71₁₀ в двоичную систему.

Получается 71₁₀ = 1000111₂.

Переведём число 81₁₀ в двоичную систему.

Получается 81₁₀ = 1010001₂.

Найдём количество единиц для каждого числа, записанного в двоичной системе.

111011₂, Кол. ед.: 5
1000111₂, Кол ед.: 4
1010001₂, Кол ед.: 3

Ответ: 3

Задача (Из десятичной в восьмеричную)

Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, сумма цифр которого в восьмеричной записи наименьшая. В ответе запишите сумму цифр в восьмеричной записи этого числа.

86₁₀, 99₁₀, 105₁₀

Решение:

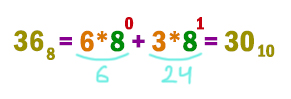
Переведём число 86₁₀ в восьмеричную систему.

Делаем аналогично тому, как мы переводили в двоичную систему, только теперь уголком делим на 8. Остатки могут получатся от 0 до 7.

Как только в результате деления получили число меньшее, чем 8, то завершаем процесс перевода.

Остатки опять записываем задом наперёд. Последнее число тоже участвует в формировании результата наравне с остатками.

Получается 86₁₀ = 126₈.

Переведём число 99₁₀ в восьмеричную систему.

Получается 99₁₀ = 143₈.

Переведём число 105₁₀ в восьмеричную систему.

Получается 105₁₀ = 151₈.

Найдём сумму цифр у полученных чисел.

126₈, Сумма цифр: 9
143₈, Сумма цифр: 8
151₈, Сумма цифр: 7

Наименьшая сумма цифр равна 7.

Ответ: 7

Разберём несколько нестандартных тренировочных задач для подготовки к 10 заданию ОГЭ по информатике.

Задача(Неожиданная)

Число 3322_n записано в системе счисления с основанием n (n > 1). Определите наименьшее возможное значение n. Для этого значения n в ответе запишите представление данного числа в десятичной системе счисления. Основание системы счисления указывать не нужно.

Решение:

Наименьшее значение n в этой задаче может быть равно 4, потому что самая большая цифра – это тройка. Мы берём на 1 больше, т.к. в четверичной системе могут применяться только цифры: 0, 1, 2, 3. Тоже самое, как в нашей родной десятичной системе могут применяться 10 цифр: от нуля, до девяти. Самая большая цифра в нашей родной десятичной системе девятка.

Осталось перевести данное число из четверичной системы в десятичную.

Ответ: 250

Задача (Уже знаем)

Число 2023_n записано в системе счисления с основанием n (n > 1). Определите значение n, при котором данное число минимально. Для этого значения n в ответе запишите представление данного числа в десятичной системе счисления. Основание системы счисления указывать не нужно.

Решение:

Здесь нужно, чтобы само число 2023_n было минимальным. Но это число будет минимальным, если мы выберем самое маленькое значение n при данных цифрах.

Самое маленькое основание системы может вновь 4. Переведём наше число 2023₄ из четверичной системы в десятичную.

Получается число 139.

Ответ: 139

Задача (Крепкий орешек)

Число 121_n записано в системе счисления с основанием n (n > 1). Определите наибольшее возможное значение n, для которого 121_n < 108₁₀. Для этого значения n в ответе запишите представления данного числа в десятичной системе счисления. Основание системы счисления указывать не нужно.

Решение:

Мы не знаем в какой системе счисления записано число. Но всё равно начнём переводить его в десятичную систему, оставив переменную n в виде неизвестной.

Попробуем подобрать n.

При n=10

1*10⁰ + 2*10¹ + 1*10² = 121 > 108₁₀

Перебор. Ну это и так было понятно.

Значит, нужно уменьшать n. Возьмём n = 9.

1*9⁰ + 2*9¹ + 1*9² = 100 < 108₁₀

Как раз получилось число, которое меньше числа 108₁₀. Это и есть наибольшее n!

В ответе просили перевести исходное число в десятичную систему. Это и есть число 100, уже всё переведено.

Ответ: 100

Задача (Не все цифры одинаковые)

Десятичное число 511 записано в системе счисления с основанием n (n > 1). Определите минимальное значение n, при котором в полученной записи числа не все цифры одинаковые. В ответе запишите запись числа в системе счисления с найденным основанием n. Основание системы счисления указывать не нужно.

Решение:

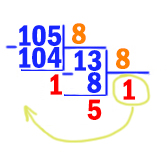
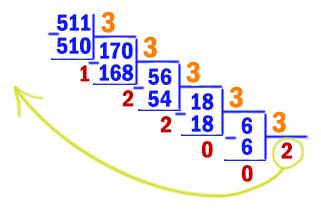
Начнём перебирать основание системы n, начиная с наименьшего значения 2. Переведём число 511₁₀ в двоичную систему.

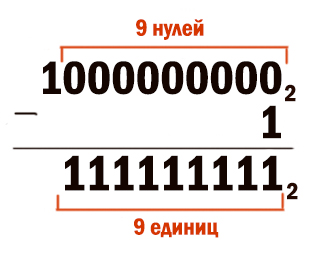
Можно переводить стандартно, через деление уголком на 2. Но в данном случае видно, что число 511 близко к 512. Число 512 = 2⁹.

Существует правило:

2⁴ = 10000₂
2⁶ = 1000000₂

Т.е. степень двойки показывает, сколько после единицы нулей у числа в двоичной системе.

Это касается любой системы счисления.

3² = 100₃
3³ = 1000₃

Наше число

511₁₀ = 512₁₀ – 1 = 2⁹ – 1 = 1000000000₂ – 1

Сделаем вычитание столбиком.

Вычитание или суммирование столбиком в любой системе счисления выполняются так же, как и в нашей системе счисления. Здесь мы вычитаем единицу из нуля. Ноль идёт занимать у более старшего разряда и т.д. В итоге обращаемся к самой старшей единице. Эта единица превращается в младшем разряде в двойку, потому что работаем в двоичной системе. Как и в нашей системе, когда занимаем у старшего разряда единицу, она превращается в десяток. В итоге каждая двойка отдаёт единицу в младший разряд. В самом младшем разряде получается действие 2-1=1. А все разряды, т.к. отдали единицу в младший разряд превратятся в 1.

Получается 511₁₀ = 200221₃.

Видим, что не все цифры у числа одинаковые в троичной системе. И число n = 3 – это минимально возможное число.

Ответ: 200221

Задача(Диапазон чисел)

Сколько существует целых чисел x, для которых выполняется неравенство

2B₁₆ < x < 62₈?

В ответе укажите только количество чисел, сами числа писать не нужно.

Решение:

Нам нужно узнать сколько чисел находятся в диапазоне от 2B₁₆ до 62₈.
Переведём числа 2B₁₆ и 62₈ в нашу родную десятичную систему счисления. Затем, мы уже сможем сообразить, сколько чисел вмещается в этот диапазон.

Чтобы перевести число из любой системы счисления в нашу родную десятичную, необходимо воспользоваться методом “возведения в степень”.

Начинаем с младшего разряда. Цифра “B” превращается в 11. 2B₁₆ = 43₁₀. Теперь переведём число
62₈ в десятичную систему.

Таким образом, наше неравенство принимает вид 43 < x < 50. Кажется, что нужно сделать 50 – 43 = 7. Но если мы подставим небольшие числа 4 < x < 6, то мы увидим, что метод 6-4=2 неверен. Число будет только одно: 5 (пять). Поэтому и от нашего числа 7 мы тоже должны отнять единицу. 7 – 1 = 6. И ответ будет 6.

Если бы у нас было в одном месте знак “больше или равно”: 2B₁₆ ≤ x < 62₈, то мы бы оставили число 7. А если было бы два знака “больше или равно”, то даже прибавили единицу.

Ответ: 6

Источник

№1 №2 №3 №4 №5 №6 №7 №8 №9 №10
№11 №12 №13 №14 №15 №16 №17 №18 №19 №20

№1 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 213₈ 2) 128₁₀+8₁₀+4₁₀ 3) 10001010₂

Ответ запишите в 10-ной системе счисления. В ответе запишите только число, основание системы счисления писать не нужно.

Замечание. Ниже приведены два решения. Выберите сами, какое нравится больше.

Решение 1. Второе число легко перевести в двоичную систему, т.к. оно задано как сумма степеней двойки. Перевод первого числа из 8-ной системы в двоичную также несложен. Поэтому сравнение удобно проводить в двоичной системе.

1) 213₈= 10001011₂ [каждая 8-ная цифра переводится в тройку двоичных цифр; нуль слева не пишем]

2) 128₁₀+8₁₀+4₁₀ = 10001100₂ [каждое слагаемое переводится в 1 в соответствующем разряде.]

3) 10001010₂

Сравниваем 3 двоичных числа, просматривая их от старших разрядов к младшим. Пять старших разрядов у всех трех чисел совпадают. В шестом слева разряде у числа 2) стоит 1, а у других чисел – 0. Поэтому число 2) – наибольшее. Далее, числа 1) и 3) различаются только в последнем разряде: у числа 1) – 1, у числа 3) – 0. Поэтому число 3) – наименьшее. Переводим числа в 10-ную систему. Получим:

2) 128₁₀+8₁₀+4₁₀= 140

3) 10001010₂ = 128₁₀+8₁₀+2₁₀= 138

Ответ: 138 [140]

Решение 2. Переведем все числа в десятичную систему и сравним.

1) 213₈= 2*64 + 1*8 + 3*1 = 128 +8 + 3 = 139₁₀

2) 128₁₀+8₁₀+4₁₀= 140₁₀

3) 10001010₂ = 128₁₀+8₁₀+2₁₀= 138₁₀

Отсюда видно, что наименьшее число – 138, а наибольшее – 140.

Ответ: 138 [140]

№2 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 322₈ 2) 3*64₁₀+16₁₀ + 1₁₀ 3) 11010000₂

Ответ запишите в 10-ной системе счисления. В ответе запишите только число, основание системы счисления писать не нужно.
Решение аналогично решению задачи № 1.

Ответ: 208 [210]

№3 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 54₈+65₈ 2) 99₁₀ 3) 1100100₂

Решение аналогично решению задачи № 1. Но в этом случае второе решение, видимо, предпочтительнее.

Ответ: 97 [100]

№4 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 157₈ 2) 112₁₀ 3) 1000110₂+101000₂

Решение аналогично решению задачи № 1.

Ответ: 110 [112]

№5 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 130₈ 2) 64₁₀ +24₁₀ +2₁₀ 3) 1011011₂

Решение аналогично решению задачи № 1.

Ответ: 88 [91]

№6 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 130₁₆ 2) 256₁₀ +48₁₀+ 3₁₀ 3) 100110010₂

Замечание. Ниже приведены два решения. Выберите сами, какое нравится больше.

Решение 1. Второе число легко перевести в 16-ную систему: первое слагаемое – это

16², а втрое – 3*16. Перевод третьего числа из 2-ной системы в 16-ную также несложен. Поэтому сравнение удобно проводить в 16-ной системе. Имеем:

1) 130₁₆

2) 256₁₀ +48₁₀+ 3₁₀ = 133₁₆

3) 3) 100110010₂ = 1 0011 0010₂= 132₁₆

Очевидно, первое число – наименьшее, а последнее – наибольшее. Переводим в десятичную систему: 130₁₆ = 256₁₀ +48₁₀ = 304₁₀; 256₁₀ +48₁₀+ 3₁₀ = 307₁₀ .

Решение 2 Так как ответ надо дать в десятичной системе счисления, сравним сначала числа 1) и 3), переведя 3) в шестнадцатеричную систему, разбив на четверки. После этого переведем наименьшее [наибольшее] в десятичную систему счисления и сравним с 2).

100110010₂=1 0011 0010₂=132₁₆.
130₁₆<132₁₆.
После сравнения в десятичной системе с 2), получим ответ: 304 [307].

Ответ: 304 [307]

№7 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 90₁₆+AA₁₆ 2) 312₁₀ 3) 100111001₂

Решение аналогично решению задачи № 6. Но решение 1 будет громоздким.

Ответ: 312 [314]

№8 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 123₁₆ 2) 292₁₀ 3) 10011111₂+10000011₂

Решение 1. Поясним, как складывать двоичные числа.

Известно, что 11111₂ + 1₂ = 100000₂. Поэтому 11111₂ + 11₂ = 100010₂. Соответственно,

10011111₂+10000011₂= 10000000₂+11111₂+10000000₂+11₂= 10000000₂+10000000₂+11111₂+11₂= 100000000₂+ 100010₂= 100100010₂= 1 0010 0010₂=122₁₆.

При этом 292₁₀ =256₁₀ + 36₁₀ = 256₁₀ + 32₁₀ +4₁₀ = 124_16.

Поэтому наибольшее из трех чисел – это число 124_16.= 292₁₀, а наименьшее – число 122₁₆= 292₁₀_.

Решение 2 аналогично решению 2 для задачи №6.

Ответ: 290 [292]

№9 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 12C₁₆+27₁₆ 2) 338₁₀ 3) 101010100₂

Решение аналогично решению задачи № 6.

Ответ: 338 [340]

№10 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 7D₁₆ 2) 64₁₀+63₁₀ 3) 1111110₂

Решение аналогично решению задачи № 6.

Ответ: 125 [127]

№11 Укажите в ответе разность наибольшего и наименьшего из следующих чисел

1) 111001000₂ 2) 711₈ 3) 1C9₁₆

Решение Переведем все числа в двоичную систему счисления:

1) 111001000₂

2) 711₈= 111 001 001₂= 111001001₂;

3) 1CA₁₆= 1 1100 1010₂= 111001010₂;

Очевидно, наибольшее число – третье, а наименьшее – первое. Они отличаются лишь в двух младших разрядах. Поэтому искомая разность равна 10₂ – 0₂= 2₁₀.

Ответ: 2

№12 Укажите в ответе разность наибольшего и наименьшего из следующих чисел

1) 10010101₂ 2) 224₈ 3) 92₁₆

Решение аналогично решению задачи № 11.

Ответ: 3

№13 Укажите в ответе разность наибольшего и наименьшего из следующих чисел

1) 11111000₂ 2) 366₈ 3) F3₁₆

Решение (набросок). Переведем все числа в двоичную систему счисления. В четырех старших разрядах у всех чисел стоит 1111. В младших разрядах у 1-го числа стоит 1000₂ ; у второго числа – 0110₂; у третьего числа – 0011₂. Поэтому наибольшее из трех чисел – первое, а наименьшее – третье. Их разность равна 1000₂– 0011₂ = 8 – 3 = 5

Ответ: 5

№14 Укажите в ответе разность наибольшего и наименьшего из следующих чисел

1) 101000001₂ 2) 513₈ 3) 146₁₆

Решение аналогично решению задачи № 13.

Ответ: 10

№15 Укажите в ответе разность наибольшего и наименьшего из следующих чисел

1) 101001101₂ 2) 514₈ 3) 14E₁₆

Решение аналогично решению задачи № 13.

Ответ: 10

№16 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 10000001₂+ 1010₂ 2) 213₈ + 1₈ 3) 87₁₆

Ответ запишите в восьмеричной системе счисления. В ответе запишите только число, основание системы счисления писать не нужно.

Решение (набросок). Переведем все числа в двоичную систему, а затем – в восьмеричную. Предварительно выполним нужные вычисления. Получим:

1) 10001011₂= 10 001 011₈= 213₈ ;

2) 214₈ ;

3) 10000111₂= 10 000 111₈= 207₈ ;

Ответ: 207 [214]

№17 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 10011111₂+100001₂ 2) 264₈+11₈ 3) C9₁₆

Решение аналогично решению № 16.

Ответ: 275 [311]

№18 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 110010000₂+101100₂ 2) 620₈+56₈ 3) 1BD₁₆

Решение аналогично решению № 16.

Ответ: 674 [676]

№19 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 100101100₂+10011₂ 2) 337₈+141₈ 3) 135₁₆

Решение аналогично решению № 16.

Ответ: 465 [500]

№20 Определите наименьшее [наибольшее] значение среди значений следующих выражений

1) 101001100₂+1000011₂ 2) 322₈+301₈ 3) 191₁₆

Решение аналогично решению № 16.

Ответ: 617 [623]

Источник

What are the smallest and the largest six-digit numbers in the Number System?

Similar Questions

123×5₁₅ + 1×233₁₅

12345₁₅+14233₁₅

Добавить комментарий Отменить ответ

What are the smallest and the largest six-digit numbers in the Number System?

Similar Questions

123×5₁₅ + 1×233₁₅

12345₁₅+14233₁₅

Вам также может понравиться

Ошибка 5в00 canon pixma как исправить

Найти сочинение как я провел каникулы

Как найти пропавшую карточку

Добавить комментарий Отменить ответ