Как найти наименьшее наибольшее значение квадратичной функции

Загрузить PDF

Во многих задачах требуется вычислить максимальное или минимальное значение квадратичной функции. Максимум или минимум можно найти, если исходная функция записана в стандартном виде: $f(x)=ax^{2}+bx+c$ или через координаты вершины параболы: $f(x)=a(x-h)^{2}+k$ . Более того, максимум или минимум любой квадратичной функции можно вычислить с помощью математических операций.

1

Запишите функцию в стандартном виде. Квадратичная функция – это функция, уравнение которой включает переменную $x^{2}$ . Уравнение может включать или не включать переменную . Если уравнение включает переменную с показателем степени больше 2, оно не описывает квадратичную функцию. Если нужно, приведите подобные члены и переставьте их, чтобы записать функцию в стандартном виде.^[1]
2
3
4

Найдите соответствующее значение f(x). Подставьте найденное значение «x» в исходную функцию, чтобы найти соответствующее значение f(x). Так вы найдете минимум или максимум функции.
5

Реклама

1

Запишите квадратичную функцию через координаты вершины параболы. Такое уравнение имеет следующий вид:^[3]
2
3

Найдите минимальное или максимальное значение функции. Если функция записана через координаты вершины параболы, минимум или максимум равен значению коэффициента . В приведенных выше примерах:
4

Реклама

1
Сначала рассмотрим стандартный вид уравнения. Запишите квадратичную функцию в стандартном виде: $f(x)=ax^{2}+bx+c$ . Если нужно, приведите подобные члены и переставьте их, чтобы получить стандартное уравнение.^[5]
- Например: $f(x)=2x^{2}-4x+1$ .
2

Найдите первую производную. Первая производная квадратичной функции, которая записана в стандартном виде, равна $f^{{prime }}(x)=2ax+b$ .^[6]
3
Производную приравняйте к нулю. Напомним, что производная функции равна угловому коэффициенту функции в определенной точке. В минимуме или максимуме угловой коэффициент равен нулю. Поэтому, чтобы найти минимальное или максимальное значение функции, производную нужно приравнять к нулю. В нашем примере:^[7]
- $f^{{prime }}(x)=4x-4$
4
5
6

Запишите ответ. Вы вычислили максимум или минимум функции. В нашем примере $f(x)=2x^{2}-4x+1$ координаты вершины равны . Коэффициент положительный, поэтому парабола направлена вверх. Следовательно, минимальное значение функции – это координата «у» вершины, которая равна .^[10]

Реклама

Советы

Ось симметрии параболы описывается уравнением x=h.

Об этой статье

Эту страницу просматривали 95 930 раз.

Была ли эта статья полезной?

Источник

Download Article

For a variety of reasons, you may need to be able to define the maximum or minimum value of a selected quadratic function. You can find the maximum or minimum if your original function is written in general form, $f(x)=ax^{2}+bx+c$ , or in standard form, $f(x)=a(x-h)^{2}+k$ . Finally, you may also wish to use some basic calculus to define the maximum or minimum of any quadratic function.

1
2

Advertisement
3
4

Find the corresponding f(x) value. Insert the value of x that you just calculated into the function to find the corresponding value of f(x). This will be the minimum or maximum of the function.
5

1

Write your quadratic function in standard or vertex form. The standard form of a general quadratic function, which can also be called the vertex form, looks like this:^[4]
2
3

Identify the minimum or maximum value. When the function is written in standard form, finding the minimum or maximum value is as simple as stating the value of the variable . For the two example functions given above, these values are:
4

1
Start with the general form. Write your quadratic function in general form, $f(x)=ax^{2}+bx+c$ . If necessary, you may need to combine like terms and rearrange to get the proper form.^[7]
- Begin with the sample function $f(x)=2x^{2}-4x+1$ .
2

Use the power rule to find the first derivative. Using basic first-year calculus, you can find the first derivative of the general quadratic function to be $f^{{prime }}(x)=2ax+b$ .^[8]
3
Set the derivative equal to zero. Recall that derivative of a function tells you the slope of the function at that selected point. The minimum or maximum of a function occurs when the slope is zero. Therefore, to find where the minimum or maximum occurs, set the derivative equal to zero. Continue with the sample problem from above:^[9]
- $f^{{prime }}(x)=4x-4$
4
5
6

Report your solution. The solution gives you the vertex of the maximum or minimum point. For this sample function, $f(x)=2x^{2}-4x+1$ , the vertex occurs at . The coefficient is positive, so the function opens upward. Therefore, the minimum value of the function is the y-coordinate of the vertex, which is .^[12]

Practice Problems and Answers

Add New Question

Question

How do you tell if a parabola is maximum or minimum?

Jake Adams

Academic Tutor & Test Prep Specialist

Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.

Academic Tutor & Test Prep Specialist

Expert Answer

Support wikiHow by
unlocking this expert answer.

First solve for a. If the value of a is a positive number, you’ll have an upward-facing parabola and you’ll need to find its minimum value. If a is a negative number, you’ll have a downward-facing parabola and you’ll need to find its maximum value.
Question

How do you tell if a parabola is up or down?

Jake Adams

Academic Tutor & Test Prep Specialist

Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.

Academic Tutor & Test Prep Specialist

Expert Answer

Support wikiHow by
unlocking this expert answer.

You can remember this concept by thinking about smiles and frowns. If someone is positive they smile, and if someone is negative, they frown. Similarly, a positive number will have an upward-facing parabola, and a negative number will have a downward-facing parabola.
Question

How do I graph a quadratic function?

First, create a data table with multiple experimental values for x. Sub in those x coordinates and get y coordinates. Plot these along the x and y axis and join the dots with a smooth curve.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

The parabola’s axis of symmetry is x = h.

References

About This Article

Article SummaryX

To find the maximum or minimum value of a quadratic function, start with the general form of the function and combine any similar terms. For example, if you’re starting with the function f(x) = 3x + 2x – x^2 + 3x^2 + 4, you would combine the x^2 and x terms to simplify and end up with f(x) = 2x^2 + 5x + 4. Now figure out which direction the parabola opens by checking if a, or the coefficient of x^2, is positive or negative. If it’s positive, the parabola opens upward. If it’s negative, the parabola opens downward. In the function f(x) = 2x^2 + 5x + 4, the coefficient of x^2 is positive, so the parabola opens upward. Next, find the x value of the vertex by solving -b/2a, where b is the coefficient in front of x and a is the coefficient in front of x^2. In the function f(x) = 2x^2 + 5x + 4, b = 5 and a = 2. Therefore, you would divide -5 by 2 times 2, or 4, and get -1.25. Finally, plug the x value into the function to find the value of f(x), which is the minimum or maximum value of the function. The function f(x) = 2x^2 + 5x + 4 would become f(-1.25) = 2(-1.25)^2 + 5(-1.25) + 4, or f(-1.25) = 0.875. If the parabola opens upward, your answer will be the minimum value. If the parabola opens downward, your answer is the maximum value. In this example, since the parabola opens upward, f(-1.25) = 0.875 is the minimum value of the function. If you want to learn how to use standard or vertex form for your formula, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 2,391,372 times.

Reader Success Stories

FantageGamer

Apr 13, 2017

“Unlike other sites or even YouTube videos, this website will break it down for you like you’re a six-year-old.…” more

Did this article help you?

Источник

Решение задач на нахождение наибольших и наименьших значений

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Квадратичная функция

Часто квадратичную функцию применяют при решении различных задач, которые сводятся к нахождению тех или иных наибольших или наименьших значений. Но перед рассмотрением таких задач стоит напомнить, какая функция является квадратичной и как найти наибольшее/наименьшее значение.

Определение 1

Функция, имеющая вид $y=ax^2+bx+c$, где $a$ не равняется нулю, называется квадратичной функцией.

График такой функции принято называть параболой. Отметим, что если $a >0$ то ее ветви будут направлены вверх и ее вершина будет принимать минимальное значение, а если $a

Наибольшее и наименьшее значение

Определение 2

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наибольшее значение в точке $x’in X$, если выполняется

[fleft(xright)le f(x’)]

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Определение 3

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наименьшее значение в точке $x’in X$, если выполняется

[fleft(xright)ge f(x’)]

Чтобы найти наименьшее и наибольшее значение заданной функции на каком либо отрезке необходимо произвести следующие действия:

Найти $f'(x)$;
Найти точки, в которых $f’left(xright)=0$;
Найти точки, в которых $f'(x)$ не будет существовать;
Выкинуть из точек, найденных в пунктах 2 и 3 те, которые не лежат в отрезке $[a,b]$;
Вычислить значения в оставшихся точках и на концах $[a,b]$;
Выбрать из этих значений наибольшее и наименьшее.

Приведем пример на нахождение наибольшего и наименьшего значения функции.

Пример 1

Найти наибольшее и наименьшее значения на [0,6]:$fleft(xright)=x^3-3x^2-45x+225$

Решение.

$f’left(xright)=3x^2-6x-45$;
$f’left(xright)=0$;

[3x^2-6x-45=0] [x^2-2x-15=0] [x=5, x=-3]
$f'(x)$ существует на всей $D(f)$;
$5in left[0,6right]$;
Значения:

[fleft(0right)=225] [fleft(5right)=50] [fleft(6right)=63]
Наибольшее значение равняется $225$, наименьшее равняется $50.$

Ответ: $max=225, min=50$.

«Решение задач на нахождение наибольших и наименьших значений» 👇

Рассмотрим далее задачи на использование наибольшего и наименьшего значений квадратичной функции.

Примеры задач

Пример 2

По перекрестным дорогам движутся два автомобиля в сторону перекрестка. Каждому автомобилю до перекрестка ехать по $50$ км. Автомобили движутся со скоростями $30$ и $40$ км/ч, соответственно. Найти, когда автомобили будут друг от друга на наименьшем расстоянии и на каком.

Решение.

Изобразим ситуацию на рисунке (рис. 1).

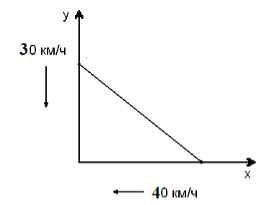
Рисунок 1.

Пусть наименьшее расстояние между автомобилями будет в момент времени $t$.

В это время одному автомобилю до перекрестка остается ехать

[50-30t км]

А второму

[50-40t км]

Расстояние между ними, по теореме Пифагора, будет равняться

[Sleft(tright)={(50-30t)}^2+{(50-40t)}^2=2500-3000t+{900t}^2+2500-4000t+{1600t}^2={2500t}^2-7000t+5000]

Найдем наименьшее значение такой функции

[t=-frac{b}{2a}=-frac{-7000}{5000}=frac{7}{5}=1,4] [Sleft(tright)=2500cdot frac{49}{25}-7000cdot frac{7}{5}+5000=4900-9800+5000=100]

Ответ: $1$ ч $24$ мин, $100$ км.

Пример 3

Найти на графике функции $y=x+2$ точку, которая дает наименьшую сумму квадратов расстояний от него до точки $(8,0)$ и $(1,0)$.

Решение.

Рассмотрим рисунок:

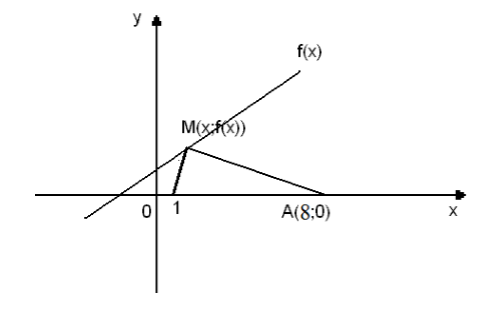
Рисунок 2.

Обозначим абсциссу искомой точки через $x$. Точка искомая точка имеет вид $(x,x+1)$.

Найдем расстояние до точки $(8,0)$: $sqrt{{(8-x)}^2+{(x+1)}^2}$

Найдем расстояние до точки $(1,0)$: $sqrt{{(1-x)}^2+{(x+1)}^2}$

Получаем, сумма равна

[Sleft(xright)={(8-x)}^2+{(x+1)}^2+{(1-x)}^2+{(x+1)}^2=64-16x+x^2+1+2x+x^2+1-2x+x^2+1+2x+x^2=4x^2+18x+67]

Наименьшее значение

[x=-frac{18}{8}=-frac{9}{4}=-2,25] [y=frac{81}{4}-frac{162}{4}+frac{268}{4}=frac{187}{4}=46,75]

Ответ: $(-2,25;46,75)$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 13.07.2022

Источник

Тип урока: урок
комплексного применения знаний.

Цели
урока.

Общеобразовательная:
           углубление и расширение знаний обучающихся
по теме «Квадратичная функция» для применения в практической
деятельности;
формирование навыков использования функционально – графического представления
для решения прикладных
задач.

Развивающая:
                                             развитие
умения логически обосновывать
рассуждения;                                                       развитие
умственных способностей, способностей к математическому творчеству путём
решения задач;                                                                                                                                                                                           развитие
коммуникативных навыков в ходе совместных действий обучающихся.

Воспитательная:
обоснование значения математики как языка для
построения математических моделей процессов и явлений окружающего мира.

В результате
ученик
знает теорему
о наибольшем (наименьшем) значении квадратичной функции и следствие из
теоремы;
умеет    иллюстрировать алгебраические условия с помощью графика,
определять наибольшее и наименьшее значение квадратичной функции, находить
область значений квадратичной функции, применять теоретические знания при
решении прикладных задач;                                                          осознаёт
  важную роль математики в развитии цивилизации и культуры.

Цели применения ИКТ:
  – наглядное
и динамическое представление учебной информации,
– повышение эффективности самостоятельной работы обучающихся,
– активизация творческого потенциала учащихся в образовательном
процессе,

I.
Мотивационно- ориентировочная часть.

1.
Актуализация знаний, умений и навыков.

Среди
данных функций выберите квадратичные функции:                                                                      1)
у = – 3х +1; 2) у = – 6х + 23; 3) у = –
0,9 х + 6,5   4) у =; 5 )у = – 8;         6) у = –+ 4х
-8.                                                                                                                         Какая
функция называется квадратичной?
    При изучении темы «Квадратичная функция и её свойства» вы научились
находить наибольшее и наименьшее значение квадратичной функции.

№1.
Определите, наибольшее или наименьшее значение принимает функция. Найдите
его. (Слайды 2,3)

– Что определяет,
наибольшее или наименьшее значение принимает квадратичная функция?

Найдите
наибольшее и наименьшее значения функции при х. (Слайд 4)

№2. Не
выполняя построения графика, определите наибольшее или наименьшее значение
принимает функция. Найдите его.

а) у =+ 4х +11; б) у = 3х – 1. (Слайд 5)

– Как
можно определить наибольшее и наименьшее значение квадратичной функции?

Выделяют
два способа нахождения наибольшего (наименьшего) значения квадратичной
функции

-по
графику функции,

-по
формуле вершины параболы.

2.
Обобщение и систематизация знаний.

–
Наибольшее или наименьшее значение принимает квадратичная функция при a0? при a?

В какой
точке функция достигает наибольшее значение? Наименьшее значение?

Сформулируйте
теорему. (Слайд 6)

При афункция принимает наименьшее значение при х = = –b/2a. Наибольшего
значения нет. Область значений: . При афункция принимает наибольшее значение при х =
= –b/2a. Наименьшего
значения нет. Область значений: .

3.Мотивация.
Задачи,
требующие определить условия, при которых некоторая величина принимает
наибольшее или наименьшее значение, часто встречается в технике,
естествознании, повседневной практической деятельности людей. Например, каких
размеров должен быть ящик, чтобы при заданном расходе материала его объём
быть наибольшим? В каком месте следует построить мост через реку, чтобы
дорога, проходящая через него и соединяющая два города, была кратчайшей?
Такие задачи имеют большое практическое значение и решаются с помощью
математики.

–
Определите и сформулируйте цели урока.

4.
Постановка учебной задачи.

Я
предлагаю вам решить задачу Дидоны. Дидона
– основательница города Карфагена и его первая царица.

(Слайд
7).

№3. Задача
Дидоны. Согласно
легенде, вынужденная бежать из своего родного города, Дидона вместе со своими
спутниками прибыла на северный берег Африки и хотела приобрести у местных
жителей место для своего нового поселения. Ей согласились уступить участок
земли, однако не больше, чем объемлет воловья шкура. Хитроумная Дидона
разрезала воловью шкуру на узенькие ремешки и, разложив их, сумела ограничить
гораздо большую площадь по сравнению с той, которую можно было бы покрыть
шкурой целиком.

(Слайд
8).

II.
Операционно-познавательная часть.

1.Моделирование.

Ученики
обсуждают план решения задачи в группах, выстраивают модель решения задачи.

Если
учесть, что Дидона выбрала участок, прилегающий к берегу моря, то на языке
математики задача (в частном случае) звучит так: предположим, что береговая
линия – прямая, ограниченный воловьими ремешками участок – прямоугольник, тогда
надо найти прямоугольник, имеющий наибольшую площадь.

2. Решение
учебно-познавательной
задачи. Пусть b – длина
воловьих ремешков,

– меньшая сторона,

– большая сторона

Наибольшую
площадь будет иметь прямоугольник со сторонами b/4 и b/2.

(Слайд
9).

– Как
должен располагаться этот прямоугольный участок по отношению к берегу:
примыкать к нему меньшей или большей стороной?

3.
Осознание общего способа действий.

–
Составьте алгоритм решения задачи.

Таким образом,
чтобы решить задачу на нахождение наибольшего (наименьшего) значения функции,
нужно

1.Составить
математическую модель
задачи.
2. Задать квадратичную
функцию.
3.Найти наибольшее (наименьшее) значение квадратичной
функции.                                                    4.Полученный
ответ соотнести с вопросом задачи.

(Слайд
10).

4.
Применение.

–
Знаете, какая геометрическая задача на нахождение наибольшего (наименьшего)
значения квадратичной функции является самой
древней? №4.
Какой из всех прямоугольников данного периметра имеет наибольшую площадь?

Решение
этой задачи было известно ещё математикам Древней
Греции.

–
Предлагаю решить эту задачу
самостоятельно. Учитель
направляет деятельность учеников, даёт индивидуальные консультации.

Решение.
                                                 Пусть х – сторона
прямоугольника, р –
периметр,                                                      тогда    – вторая
сторона.
                                                                                                                                                                                                                                                                                             ;
– первая сторона прямоугольника
;                                                                                                        – вторая
сторона.
Ответ: квадрат со стороной.

(Слайд
11).

– Кто
успешно справился с задачей?
                                – У кого возникли трудности?
Какие?                                                              Обобщим
полученный результат. Замените слова «стороны прямоугольника» словами «два
положительных числа», «периметр» – «сумма чисел»,                 «площадь»
– «произведение». Сформулируйте следствие из теоремы.

(Слайд12).

Применим
полученные знания к решению физической задачи.

№5.
Расстояние между пунктами А и В, расположенными на прямой магистрали, 9км.
Из А в В выходит автомашина со скоростью 40 км/ч, одновременно из В в том же
направлении выезжает мотоциклист с постоянным ускорением 32 км/ч. Определите
наибольшее расстояние, которое может быть между автомашиной и мотоциклистом в
течение первых двух часов движения.

(Слайд
13).

Учитель
предлагает составить математическую модель задачи. Организует индивидуальную
работу учащихся, по необходимости – работу консультантов.

Решение.
                                                                                                       Машина
находится от пункта А на расстоянии 40t
км,                                             мотоциклист на расстоянии (16+9)км.

S== =16

Расстояние
между ними у =/16+9 – 40t/

=5/4

=16

Ответ:
16км.

(Слайд
14).

III.Рефлексивно
– оценочная часть.

1.Подведение
итогов.

– Что
нового вы узнали на уроке? Чему научились?

– Какие
цели были поставлены в начале урока? Удалось ли их достичь?

2.Самооценка
усвоения материала.

Оцените
по 5-бальной шкале свой вклад в решение общей учебной задачи.

3.Планирование
дальнейшей деятельности в изучении темы.

На двух
последующих уроках мы будем применять теорему о наибольшем (наименьшем)
значении функции при решении заданий с параметрами.

4.Задание
на дом.

1.
Докажите теорему и следствие из неё.

2. №6.
Докажите, что из всех треугольников данного периметра наибольшую площадь
имеет равносторонний.

4.
Творческое задание. Представьте решение задачи практического содержания на
нахождение наибольшего и наименьшего значения квадратичной функции.

(Слайд
15).

Учитель
выставляет оценки, благодарит обучающихся за работу.

5.
Рефлексия.

В конце урока обучающимся
предложено
ответить на вопросы. (Слайд 16).

1.Бурмистрова Т.А. Программы
общеобразовательных учреждений. Алгебра 7-9 классы. – М.: Просвещение,2012.

2.Макарычев Ю.Н. и др. Учебник Алгебра 9 класс.
– М.: Просвещение, 2012.

3.Шарыгин И.Ф. Факультативный курс по
математике. – М.; Просвещение, 2009.

4. Кузнецова Л.В. и др. Алгебра. Сборник
заданий для ГИА в 9классе. – М.: Просвещение, 2010.

5. Студенецкая В.Н., Сагателова Л.С.
Сборник элективных курсов. Математика 8-9 классы.- Волгоград: Учитель,2007.

6.Костерина Н.П. Задачи повышенной трудности
в курсе алгебры 7-9 классов. – М.: Просвещение, 1991.

7.Иванова Т.А. Современный урок
математики: теория, технология, практика. – Н. Новгород: НГПУ, 2010.

8.Мичасова М.А., Малышев И.Г., Иванов
Б.Н. подготовка к ЕГЭ по математике. ЗаданияС1-С6. – Н.Новгород: НИРО, 2010

Ресурсы
сети Интернет.

Источник

Главная

» 2015 » Октябрь » 1 » Как найти максимум или минимум квадратичной функции

03:35

Как найти максимум или минимум квадратичной функции

3 методика:Квадратичная функция вида y = ax2 + bx + cКвадратичная функция вида y = a(x-h)2 + kПримеры

Координата «у» вершины параболы и есть максимум или минимум квадратичной функции (график которой – парабола).

Шаги

Метод 1 из 3: Квадратичная функция вида y = ax2 + bx + c

1
Определите, что вы ищите – максимум или минимум, так как вы не можете искать сразу оба значения.

Метод 2 из 3: Квадратичная функция вида y = a(x-h)2 + k

1
В случае квадратичной функции вида y = a(x-h)2 + k коэффициент «k» и есть максимум или минимум функции.
- «k» является максимумом, если коэффициент «а» – отрицательный; «k» является минимумом, если коэффициент «а» – положительный.

Метод 3 из 3: Примеры

1
Найдите максимум или минимум функции f(x) = x2 + x + 1.
- так как а=1, то вы ищите минимум. Подставляете b=1 и c=1 в формулу (c – b2/4a) и находите, что минимум данной функции равен 3/4.
2
Найдите максимум или минимум функции f(x) = -2(x-1)2 + 3.
- так как а=-2, то вы ищите максимум, который равен значению коэффициента k. Ответ: максимум данной функции равен 3.

Советы

Ось симметрии параболы: х = h.
Значение коэффициента «k» соответствует максимальному или минимальному значению функции.

Категория: Вопросы и ответы |
Просмотров: 3258 |

| Рейтинг: 0.0/0

Добавлять комментарии могут только зарегистрированные пользователи.

[

Регистрация

Вход

]

Источник

Советы

Об этой статье

Была ли эта статья полезной?

Practice Problems and Answers

References

About This Article

Reader Success Stories

Did this article help you?

Решение задач на нахождение наибольших и наименьших значений

Квадратичная функция

Наибольшее и наименьшее значение

Примеры задач

Как найти максимум или минимум квадратичной функции

Шаги

Метод 1 из 3: Квадратичная функция вида y = ax2 + bx + c

Метод 2 из 3: Квадратичная функция вида y = a(x-h)2 + k

Метод 3 из 3: Примеры

Советы

Вам также может понравиться

Как найти по номеру телефона через мтс

Кривизна ног у детей как исправить

Прыгает стрелка тахометра как исправить

Добавить комментарий Отменить ответ