НОК чисел онлайн
Наименьшим общим кратным(НОК) натуральных чисел называется наименьшее натуральное число которое делится на эти числа без остатка
Выберите количество чисел для нахождения НОК
2 числа3 числа4 числа5 чисел6 чисел
Введите числа
Нахождение НОК двух чисел с помощью разложения на простые множители
1) Для начала нужно каждое число разложить на простые множители
2) Потом подчеркнуть множители второго числа которых нет в первом
3) Перемножить множители первого числа с подчёркнутыми множителями второго
4) Наименьшим общим кратным будет произведение простых множителей первого числа и простых множителей второго числа которые не вошли в первое
Разберём пример
Найдём НОК(4,6)
Разложим числа
4 = 2 × 2
6 = 2 × 3
Подчеркнём множители которых нет в первом числе
6 = 2 × 3
Перемножим множители первого числа с подчёркнутыми множителями второго
НОК(4, 6) = 2 × 2 × 3 = 12
НОК 3 чисел и более
Всё по аналогии с 2 числами
Разберём пример
Найдём НОК(4,6,30)
Разложим числа
4 = 2 × 2
6 = 2 × 3
30 = 2 × 3 × 5
Подчеркнём множители которых нет в первом числе
6 = 2 × 3
30 = 2 × 3 × 5
Перемножим множители первого числа с подчёркнутыми множителями второго
НОК(4, 6, 30) = 2 × 2 × 3 × 5 = 60
Что может калькулятор ?
Находить НОК 2 чисел
Находить НОК 3 чисел
Находить НОК 4 чисел
Находить НОК 5 чисел
Находить НОК 6 чисел
Отображает алгоритм нахождения НОК
Похожие калькуляторы
Нахождение НОД и НОК чисел
Онлайн-калькулятор “Нахождение НОД и НОК чисел“. Наш калькулятор поможет вам найти наибольший общий делить (НОД) и наименьшее общее кратное (НОК) чисел. Особенностью данного калькулятора является то, что он может находить НОК и НОД не только двух чисел, но и трех или четырех чисел. Введите натуральные числа и нажмите кнопку “Вычислить” и наш калькулятор не просто выдаст ответ, но и представит подробное решение, где последовательно будет изложен порядок нахождения НОД и НОК чисел.
Выберите количество чисел, для которых требуется найти НОД и НОК:
2 числа
3 числа
4 числа
| Первое число | Второе число |
Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое эти числа делятся без остатка. Наибольший общий делитель обозначается следующим образом: НОД (18; 48) = 6
Наименьшее общее кратно нескольких чисел – это самое меньшее число, которое делится на каждое из этих чисел без остатка. Например: НОК (18; 48) = 144
Это следует знать!
Как определить, что число делится на 3 без остатка? Очень просто – на 3 делятся только те числа, сумма цифр которых делится на 3. Например: число 795 делится на 3, так как сумма его цифр 7 + 9 + 5 = 21 делится на 3.
21 : 3 = 7
Наименьшее общее кратное
- Общее кратное
- Наименьшее общее кратное
- Как найти НОК
- С помощью разложения на простые множители
- Нахождение НОК через НОД
- Калькулятор НОК
Общее кратное
Число может быть кратно не одному, а сразу нескольким числам, такое число называется общим кратным данных чисел.
Пример.
Числу 3 кратны числа: 6, 9, 12, 15 и т. д.
Числу 4 кратны числа: 8, 12, 16, 20 и т. д.
Можно заметить, что одно и тоже число (12) делится нацело сразу на оба числа 3 и 4. Следовательно, число 12 есть общее кратное чисел 3 и 4.
Общее кратное чисел — это любое число, которое делится без остатка на каждое из данных чисел.
Найти общее кратное нескольких натуральных чисел достаточно легко, можно просто перемножить данные числа, полученное произведение и будет их общим кратным.
Пример. Найти общее кратное для чисел 2, 3, 4, 6.
Решение:
2 · 3 · 4 · 6 = 144.
Число 144 — общее кратное чисел 2, 3, 4 и 6.
Для любого количества натуральных чисел существует бесконечно много кратных.
Пример. Для чисел 12 и 20 кратными будут числа: 60, 120, 180, 240 и т. д. Все они являются общими кратными для чисел 12 и 20.
Наименьшее общее кратное
Наименьшее общее кратное (НОК) нескольких чисел — это самое маленькое натуральное число, которое делится без остатка на каждое из этих чисел.
Пример. Наименьшим общим кратным чисел 3, 4 и 9 является число 36, никакое другое число меньше 36 не делится одновременно на 3, 4 и 9 без остатка.
Наименьшее общее кратное записывается так:
НОК (a, b, …) = x.
Числа в круглых скобках могут быть указаны в любом порядке.
Пример. Запишем наименьшее общее кратное чисел 3, 4 и 9:
НОК (3, 4, 9) = 36.
Как найти НОК
Рассмотрим два способа нахождения наименьшего общего кратного: с помощью разложения чисел на простые множители и нахождение НОК через НОД.
С помощью разложения на простые множители
Чтобы найти НОК нескольких натуральных чисел, надо разложить эти числа на простые множители, затем взять из этих разложений каждый простой множитель с наибольшим показателем степени и перемножить эти множители между собой.
Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.
Решение: разложим каждое из этих чисел на простые множители:
99 = 3 · 3 · 11 = 32 · 11,
54 = 2 · 3 · 3 · 3 = 2 · 33.
Наименьшее общее кратное должно делиться на 99, значит, в его состав должны входить все множители числа 99. Далее НОК должно делиться и на 54, т. е. в его состав должны входить множители и этого числа.
Выпишем из этих разложений каждый простой множитель с наибольшим показателем степени и перемножим эти множители между собой. Получим следующее произведение:
2 · 33 · 11 = 594.
Это и есть наименьшее общее кратное данных чисел. Никакое другое число меньше 594 не делится нацело на 99 и 54.
Ответ: НОК (99, 54) = 594.
Так как взаимно простые числа не имеют одинаковых простых множителей, то их наименьшее общее кратное равно произведению этих чисел.
Пример. Найдите наименьшее общее кратное двух чисел 12 и 49.
Решение: разложим каждое из этих чисел на простые множители:
12 = 2 · 2 · 3 = 22 · 3,
49 = 7 · 7 = 72.
Применяя к этому случаю правило, мы придём к заключению, что взаимно простые числа надо просто перемножить:
22 · 3 · 72 = 12 · 49 = 588.
Ответ: НОК (12, 49) = 588.
Таким же образом надо поступать, когда нужно найти наименьшее общее кратное простых чисел.
Пример. Найдите наименьшее общее кратное чисел 5, 7 и 13.
Решение: так как данные числа являются простыми, то просто перемножим их:
5 · 7 · 13 = 45.
Ответ: НОК (5, 7, 13) = 455.
Если большее из данных чисел делится на все остальные числа, то это число и будет наименьшим общим кратным данных чисел.
Пример. Найдите наименьшее общее кратное чисел 24, 12 и 4.
Решение: разложим каждое из этих чисел на простые множители:
24 = 2 · 2 · 2 · 3 = 23 · 3,
12 = 2 · 2 · 3 = 22 · 3,
4 = 2 · 2 = 22.
Можно заметить, что разложение большего числа содержит все множители остальных чисел, значит большее из этих чисел делится на все остальные числа (в том числе и само на себя) и является наименьшим общим кратным:
23 · 3 = 24.
Ответ: НОК (24, 12, 4) = 24.
Нахождение НОК через НОД
НОК двух натуральных чисел равно произведению этих чисел, поделённого на их НОД.
Правило в общем виде:
НОК (m, n) = m · n : НОД (m, n)
Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.
Решение: сначала находим наибольший общий делитель:
НОД (99, 54) = 9.
Теперь мы можем вычислить НОК этих чисел по формуле:
НОК (99, 54) = 99 · 54 : НОД (99, 54) = 5346 : 9 = 594.
Ответ: НОК (99, 54) = 594.
Чтобы найти НОК трёх или более чисел используется следующий порядок действий:
- Находят НОК любых двух из данных чисел.
- Затем находят наименьшее общее кратное найденного НОК и третьего числа и т. д.
- Таким образом поиск НОК продолжается до тех пор, пока есть числа.
Пример. Найдите наименьшее общее кратное чисел 8, 12 и 9.
Решение: сначала находим наибольший общий делитель любых двух из этих чисел, например, 12 и 8:
НОД (12, 8) = 4.
Вычисляем их НОК по формуле:
НОК (12, 8) = 12 · 8 : НОД (12, 8) = 96 : 4 = 24.
Теперь найдём НОК числа 24 и оставшегося числа 9. Их НОД:
НОД (24, 9) = 3.
Вычисляем НОК по формуле:
НОК (24, 9) = 24 · 9 : НОД (24, 9) = 216 : 3 = 72.
Ответ: НОК (8, 12, 9) = 72.
Калькулятор НОК
Данный калькулятор поможет вам найти наименьшее общее кратное чисел. Просто введите числа через пробел или запятую и нажмите кнопку Вычислить НОК
.
Для того, чтобы находить общий знаменатель
при
сложении
и
вычитании дробей с разными
знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).
Кратное числу «a» — это число, которое
само делится на число «a» без остатка.
Числа кратные 8
(то есть, эти числа разделятся на 8 без остатка):
это числа 16, 24, 32 …
Кратные 9: 18, 27, 36, 45 …
Чисел, кратных данному числу a бесконечно много, в отличии от делителей
этого же числа. Делителей —
конечное количество.
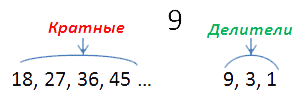
Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.
Запомните!
![]()
Наименьшим общим кратным (НОК) двух и более натуральных
чисел называется наименьшее натуральное число, которое само
делится нацело на каждое из этих чисел.
Как найти НОК
НОК можно найти и записать двумя способами.
Первый способ нахождения НОК
Данный способ обычно применяется для небольших чисел.
- Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое
для обоих чисел. - Кратное числа «a»
обозначаем большой буквой «К».К (a) = {…, …}
Пример. Найти НОК 6 и 8.
К (6) = {12, 18, 24, 30, …}
К (8) = {8, 16, 24, 32, …}
НОК (6, 8) = 24
Второй способ нахождения НОК
Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.
- Разложить данные числа на простые множители.
Подробнее правила разложения на
простые множители вы можете прочитать в теме
как найти наибольший общий делитель (НОД).
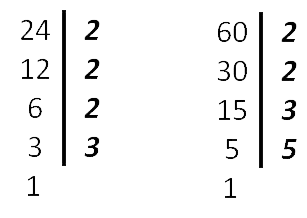
- Выписать в строчку множители, входящие в разложение
самого большого из чисел, а под ним —
разложение остальных чисел.Запомните!

Количество одинаковых множителей в разложениях чисел может быть разное.
60 = 2 · 2 · 3 · 5
24 = 2 · 2 · 2 · 3
- Подчеркнуть в разложении
меньшего числа (меньших чисел) множители,
которые не вошли в разложение бóльшего числа
(в нашем примере это 2) и добавить эти множители в разложение бóльшего числа.
НОК (24, 60) = 2 · 2 · 3 · 5 · 2 - Полученное произведение записать в ответ.
Ответ: НОК (24, 60) = 120
Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24).
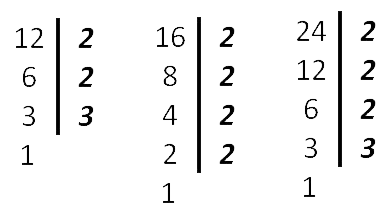
24 = 2 · 2 · 2 · 3
16 = 2 · 2 · 2 · 2
12 = 2 · 2 · 3
Как видим из разложения чисел, все множители 12 вошли в
разложение 24
(самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из
разложения числа 16.
НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48
Ответ: НОК (12, 16, 24) = 48
Особые случаи нахождения НОК
- Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.
Например, НОК (60, 15) = 60
- Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее
кратное равно произведению этих чисел.Пример.
НОК (8, 9) = 72
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
5 сентября 2020 в 15:37
Елена Елена

Профиль
Благодарили: 0
Сообщений: 1

Елена Елена
Профиль
Благодарили: 0
Сообщений: 1
НОК(360,102)
0
Спасибо
Ответить
6 сентября 2020 в 13:42
Ответ для Елена Елена
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
360 = 23 · 32 · 5; 102 = 2 · 3 · 17.
НОК(360; 102) = 23 · 32 · 5 · 17 = …
0
Спасибо
Ответить
30 мая 2018 в 17:34
Тамара Татарникова

Профиль
Благодарили: 0
Сообщений: 1

Тамара Татарникова
Профиль
Благодарили: 0
Сообщений: 1
Найдите четырёхзначное число, которое кратно 24, а произведение цифр этого числа равно 16, в ответ дайте какое-нибудь одно число.
Я написала 1242, но 1242 при делении на 24 дает в ответе 51,75 будет ли это верным ответом?
0
Спасибо
Ответить
3 июня 2018 в 1:58
Ответ для Тамара Татарникова
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
1128 1224 8112
0
Спасибо
Ответить
29 ноября 2016 в 14:47
Анвар Тынайбеков

Профиль
Благодарили: 0
Сообщений: 1

Анвар Тынайбеков
Профиль
Благодарили: 0
Сообщений: 1
НОК(344и170)=
0
Спасибо
Ответить
2 декабря 2016 в 8:23
Ответ для Анвар Тынайбеков
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
1
Спасибо
Ответить
15 февраля 2016 в 19:02
Кирилл Журавлёв

Профиль
Благодарили: 1
Сообщений: 3

Кирилл Журавлёв
Профиль
Благодарили: 1
Сообщений: 3
число 123 454 321 делится на 11 111. найдите нок этих чисел
1
Спасибо
Ответить
15 февраля 2016 в 19:08
Ответ для Кирилл Журавлёв
Кирилл Журавлёв

Профиль
Благодарили: 1
Сообщений: 3

Кирилл Журавлёв
Профиль
Благодарили: 1
Сообщений: 3
12132211
0
Спасибо
Ответить
19 сентября 2016 в 12:55
Ответ для Кирилл Журавлёв
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Здесь подробно описано нахождение НОК.
А в супер-решателе можно себя проверить.
0
Спасибо
Ответить
15 февраля 2016 в 18:51
Кирилл Журавлёв

Профиль
Благодарили: 1
Сообщений: 3

Кирилл Журавлёв
Профиль
Благодарили: 1
Сообщений: 3
ЧИСЛО 123 454 321 ДЕЛИТСЯ 11 111. НАЙДИТЕ НОК ЭТИХ ЧИСЕЛ НЕ ВЫПОЛНЯЯ РАЗЛОЖЕНИЯ ЧИСЕЛ НА ПРОСТЫЕ МНОЖИТЕЛИ
0
Спасибо
Ответить
19 сентября 2016 в 12:56
Ответ для Кирилл Журавлёв
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
27 января 2016 в 18:15
Lera Kuchinskaya

Профиль
Благодарили: 0
Сообщений: 1

Lera Kuchinskaya
Профиль
Благодарили: 0
Сообщений: 1
НОК 100 150 250![]()
0
Спасибо
Ответить
27 января 2016 в 22:36
Ответ для Lera Kuchinskaya
Виктория Казимирова

Профиль
Благодарили: 0
Сообщений: 1

Виктория Казимирова
Профиль
Благодарили: 0
Сообщений: 1
А что за цифры!!!?
0
Спасибо
Ответить
28 января 2016 в 16:00
Ответ для Lera Kuchinskaya
Anton Wuckert

Профиль
Благодарили: 0
Сообщений: 1

Anton Wuckert
Профиль
Благодарили: 0
Сообщений: 1
НОК = 1500
0
Спасибо
Ответить
19 сентября 2016 в 11:42
Ответ для Lera Kuchinskaya
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для решения можно воспользоваться решателем на сайте.
0
Спасибо
Ответить
22 января 2016 в 13:46
Андрей Алексеев

Профиль
Благодарили: 0
Сообщений: 1

Андрей Алексеев
Профиль
Благодарили: 0
Сообщений: 1
числа 4,5,6,7,10,12,15,16,20,50, которые являются делителями 24 и кратными 2
0
Спасибо
Ответить
23 января 2016 в 13:33
Ответ для Андрей Алексеев
Александра Сирота

Профиль
Благодарили: 0
Сообщений: 2

Александра Сирота
Профиль
Благодарили: 0
Сообщений: 2
ОТВЕТ: 4 и 12
0
Спасибо
Ответить
24 января 2016 в 13:41
Ответ для Андрей Алексеев
Инна Шабрашина

Профиль
Благодарили: 0
Сообщений: 5

Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
6 ,2, 12
0
Спасибо
Ответить
25 января 2016 в 19:52
Ответ для Андрей Алексеев
Нелия Ахмедова

Профиль
Благодарили: 0
Сообщений: 1

Нелия Ахмедова
Профиль
Благодарили: 0
Сообщений: 1
6,12.
0
Спасибо
Ответить
19 сентября 2016 в 10:59
Ответ для Андрей Алексеев
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Чтобы не запутаться, необходимо каждое из чисел проверить на оба условия:
1) 4 — 24/4=6 — делитель 24. 4/2=2 — кратно 2.
2) 5 — 24/5=не делится без остатка — не делитель. 5/2 — не делится без остатка — не кратно 2.
И так далее.
Ответ: 4,6,12.
0
Спасибо
Ответить
23 декабря 2015 в 17:00
Евгений Мухамедшин

Профиль
Благодарили: 0
Сообщений: 1

Евгений Мухамедшин
Профиль
Благодарили: 0
Сообщений: 1
1) (4/15+5/8)-3/5
2) (1/5+13/16)-9/20
0
Спасибо
Ответить
19 сентября 2016 в 10:01
Ответ для Евгений Мухамедшин
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для нахождения НОК можно воспользоваться супер-решателем. Раскрываем скобки и приводим к общему знаменателю.
1) ===0
2) ===
0
Спасибо
Ответить
17 ноября 2015 в 6:29
Светлана Каблучко

Профиль
Благодарили: 0
Сообщений: 1

Светлана Каблучко
Профиль
Благодарили: 0
Сообщений: 1
запишите числа удовлетворяющие двойное неравенство 354<х<361 если известно что они кратны 2,5,10
0
Спасибо
Ответить
24 ноября 2015 в 17:56
Ответ для Светлана Каблучко
Тима Клюев

Профиль
Благодарили: 0
Сообщений: 8

Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
360
0
Спасибо
Ответить
Наименьшее о́бщее кратное (HOK) двух целых чисел — это наименьшее натуральное число, которое делится на оба без остатка, то есть кратно им обоим. К примеру, для чисел 6 и 4, наименьшим общим кратным будет 12.
Как найти НОК?
Способов найти НОК несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОК при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:
- разложить оба числа на простые множители;
- выбрать одну группу множителей;
- добавить к ним множители из второй группы, которые отсутствуют в выбранной;
- найти их произведение.
Примеры нахождения наименьшего общего кратного
Рассмотрим приведенный алгоритм на конкретных примерах:
Пример 1: найти НОК 4 и 6
1. Раскладываем 6 и 4 на простые множители:
2. Возьмем первую группу множителей: 2 · 3.
3. Смотрим вторую группу (2 · 2) и видим, что из двух двоек, одна присутствует в первом разложении. Таким образом, берем только одну двойку. Добавляем к первому разложению и получаем: 2 · 3 · 2
4. Вычисляем произведение: 2 · 3 · 2 = 12.
Ответ: НОК (6; 4) = 12
Пример 2: найти НОК 32 и 20
1. Раскладываем 32 и 20 на простые множители:
2. Возьмем первую группу множителей: 2 · 2 · 2 · 2 · 2.
3. Смотрим вторую группу (2 · 2 · 5) и видим, что из двух двоек и пятерки, обе двойки присутствуют в первом разложении. Таким образом, берем только пятерку. Добавляем к первому разложению и получаем: 2 · 3 · 2
4. Вычисляем произведение: 2 · 2 · 2 · 2 · 2 · 5 = 160.
Ответ: НОК (32; 20) = 160
