Как найти наименьшее общее кратное пример

Что такое нок в математике? Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы узнаем, как найти наименьшее общее кратное, какие есть для этого способы для трех чисел и более, разберем вопрос о том, как находить НОК отрицательного числа. Также разберемся, что такое нок и нод, как найти нок и нод. 

Вычисление наименьшего общего кратного (НОК) через НОД

Мы уже узнали, что такое нок, а также установили связь наименьшего общего кратного с наибольшим общим делителем (кратность показывает в расчетах во сколько раз один показатель больше другого). Теперь как настоящие математики научимся определять НОК через НОД (нок и нод чисел натуральных). Сначала разберемся, как найти нок для положительных чисел. Сделать это можно и онлайн или на калькуляторе, но лучше научиться самостоятельно.

Поиск наименьшего общего кратного через наибольший общий делитель можно по формуле НОК(a, b)=a·b:НОД(a, b).

В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.

Нахождение НОК с помощью разложения чисел на простые множители

Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители. Перед тем, как это узнавать, дадим небольшое определение. 

Этот способ нахождения наименьшего общего кратного основан на равенстве НОК(a, b)=a·b:НОД(a, b). Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.

Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.

Вернемся к числам 75 и 210, для которых мы уже пробовали искать НОК в одном из прошлых примеров. Разложим их на простые множители: 75=3·5·5 и 210=2·3·5·7. К произведению множителей 3, 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210. Получаем: 2·3·5·5·7. Это и есть НОК чисел 75 и 210.

Нахождение НОК трех и большего количества чисел

Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.

Предположим, что у нас есть целые числа a1, a2, …, ak. НОК mk этих чисел находится при последовательном вычислении m2=НОК(a1, a2), m3=НОК(m2, a3), …, mk=НОК(mk−1, ak).

Теперь рассмотрим, как можно применять теорему для решения конкретных задач.

Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.

Нахождение наименьшего общего кратного отрицательных чисел

Для того чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.

НОК(54, −34)=НОК(54, 34), а НОК(−622, −46, −54, −888)=НОК(622, 46, 54, 888).

Такие действия допустимы в связи с тем, что если принять, что a и −a – противоположные числа,
то  множество кратных числа a совпадает со множеством кратных числа −a.

Наименьшее о́бщее кратное (HOK) двух целых чисел — это наименьшее натуральное число, которое делится на оба без остатка, то есть кратно им обоим. К примеру, для чисел 6 и 4, наименьшим общим кратным будет 12.

Как найти НОК?

Способов найти НОК несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОК при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:

1. разложить оба числа на простые множители;
2. выбрать одну группу множителей;
3. добавить к ним множители из второй группы, которые отсутствуют в выбранной;
4. найти их произведение.

Примеры нахождения наименьшего общего кратного

Рассмотрим приведенный алгоритм на конкретных примерах:

Пример 1: найти НОК 4 и 6

2. Возьмем первую группу множителей: 2 · 3.

3. Смотрим вторую группу (2 · 2) и видим, что из двух двоек, одна присутствует в первом разложении. Таким образом, берем только одну двойку. Добавляем к первому разложению и получаем: 2 · 3 · 2

4. Вычисляем произведение: 2 · 3 · 2 = 12.

Ответ: НОК (6; 4) = 12

Пример 2: найти НОК 32 и 20

2. Возьмем первую группу множителей: 2 · 2 · 2 · 2 · 2.

3. Смотрим вторую группу (2 · 2 · 5) и видим, что из двух двоек и пятерки, обе двойки присутствуют в первом разложении. Таким образом, берем только пятерку. Добавляем к первому разложению и получаем: 2 · 3 · 2

4. Вычисляем произведение: 2 · 2 · 2 · 2 · 2 · 5 = 160.

Ответ: НОК (32; 20) = 160

Для того, чтобы находить общий знаменатель
при
сложении
и
вычитании дробей с разными
знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).

Кратное числу «a» — это число, которое
само делится на число «a» без остатка.

Числа кратные 8
(то есть, эти числа разделятся на 8 без остатка):
это числа 16, 24, 32 …

Кратные 9: 18, 27, 36, 45 …

Чисел, кратных данному числу a бесконечно много, в отличии от делителей
этого же числа. Делителей —
конечное количество.

Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.

Как найти НОК

НОК можно найти и записать двумя способами.

Первый способ нахождения НОК

Данный способ обычно применяется для небольших чисел.

1. Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое
   для обоих чисел.
2. Кратное числа «a»
   обозначаем большой буквой «К».

   К (a) = {…, …}

Пример. Найти НОК 6 и 8.

К (6) = {12, 18, 24, 30, …}

К (8) = {8, 16, 24, 32, …}

НОК (6, 8) = 24

Второй способ нахождения НОК

Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.

1. Разложить данные числа на простые множители.
   Подробнее правила разложения на
   простые множители вы можете прочитать в теме
   как найти наибольший общий делитель (НОД).
   
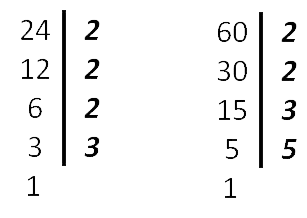
2. Выписать в строчку множители, входящие в разложение
   самого большого из чисел, а под ним —
   разложение остальных чисел.

   Запомните!
   

   Количество одинаковых множителей в разложениях чисел может быть разное.

   60 = 2 · 2 · 3 · 5

   24 = 2 · 2 · 2 · 3

3. Подчеркнуть в разложении
   меньшего числа (меньших чисел) множители,
   которые не вошли в разложение бóльшего числа
   (в нашем примере это 2) и добавить эти множители в разложение бóльшего числа.
   
   НОК (24, 60) = 2 · 2 · 3 · 5 · 2
4. Полученное произведение записать в ответ.
   
   Ответ: НОК (24, 60) = 120

Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24).

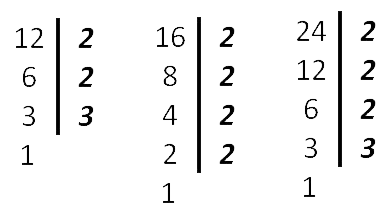
24 = 2 · 2 · 2 · 3

16 = 2 · 2 · 2 · 2

12 = 2 · 2 · 3

Как видим из разложения чисел, все множители 12 вошли в
разложение 24
(самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из
разложения числа 16.

НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48

Ответ: НОК (12, 16, 24) = 48

Особые случаи нахождения НОК

1. Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.

   Например, НОК (60, 15) = 60

2. Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее
   кратное равно произведению этих чисел.

   Пример.

   НОК (8, 9) = 72

---

Ваши комментарии

Оставить комментарий:

---

Наименьшее общее кратное (сокр. НОК) в математике определяется для нескольких чисел. Это наименьшее натуральное число, делящееся на каждое их данных чисел без остатка. Для того, чтобы найти наименьшее общее кратное нужно: 1) Разложить каждое число на простые множители. 2) Домножить одно из чисел на те множители, которые не входят в его разложение, но входят в разложение других чисел. Пример Требуется найти наименьшее общее кратное для трёх чисел: 6, 10 и 15. 1) Разложим числа на простые множители. 6 = 2 * 3. 10 = 2 * 5. 15 = 3 * 5. 2) Возьмём число 6. Множитель, который не входит в разложение данного числа, но входит в разложение чисел 10 и 15 – это число 5. Домножаем число 6 на число 5 – получаем 30. Следовательно, НОК (6, 10, 15) = 30. Другой способ Если требуется найти наименьшее общее кратное двух чисел, то можно поступить таким образом: 1) Умножить одно число на другое. 2) Разделить полученное произведение на НОД (наибольший общий делитель). Найдём наименьшее общее кратное чисел 8 и 6. 1) 8 * 6 = 48. 2) 8 = 2 * 2 * 2 и 6 = 2 * 3 -> НОД (8, 6) = 2. НОК (8, 6) = 48 / 2 = 24. автор вопроса выбрал этот ответ лучшим дольф­аника [379K] 8 лет назад  Складывать, умножать, делить, приводить к общему знаменателю и другие арифметические действия очень увлекательное занятие, особенно восхищают примеры, занимающие целый лист. Итак найти общее кратное для двух чисел, которое будет являться самым маленьким числом на которое делятся два числа. Хочу заметить, что не обязательно в дальнейшем прибегать к формулам, чтобы найти искомое, если можешь считать в уме (а это можно натренировать), то цифры сами всплывают в голове и потом дроби щелкаются как орешки. Для начала усвоим, что можно умножить два числа друг на друга, а потом эту цифру уменьшать и делить поочередно на данные два числа, так мы найдем наименьшее кратное. Например, два числа 15 и 6. Умножаем и получаем 90. Это явно больше число. Причем 15 делится на 3 и 6 делится на 3, значит 90 тоже делим на 3. Получаем 30. Пробуем 30 разделить 15 равно 2. И 30 делим 6 равно 5. Так как 2 это предел, то получается, что наименьшее кратное для чисел 15 и 6 будет 30. С цифрами побольше будет немного трудней. но если знать, какие цифры дают нулевой остаток при делении или умножении, то трудностей, в принципе, больших нет. НОК, или наименьшее общее кратное, – это наименьшее натуральное число двух и более чисел, которое делится на каждое из данных чисел без остатка. Вот пример того, как найти наименьшее общее кратное 30 и 42. Первым делом нужно разложить данные числа на простые множители. Для 30 – это 2 х 3 х 5. Для 42 – это 2 х 3 х 7. Так как 2 и 3 имеются в разложении числа 30, то вычеркиваем их. Выписываем множители, которые входят в разложение числа 30. Это 2 х 3 х 5 . Теперь нужно домножить их на недостающий множитель, который имеем при разложении 42,а это 7. Получаем 2 х 3 х 5 х 7. Находим, чему равно 2 х 3 х 5 х 7 и получаем 210. В итоге получаем, что НОК чисел 30 и 42 равен 210. CooLW­arK [27.3K] 9 лет назад  Представляю ещё один способ нахождения наименьшего общего кратного. Рассмотрим его на наглядном примере. Необходимо найти НОК сразу трёх чисел: 16, 20 и 28. Представляем каждое число как произведение его простых множителей: 16 = 2·2·4 20 = 2·2·5 28 = 2·2·7 Записываем степени всех простых множителей: 16 = 2·2·4 = 2^2·4^1 20 = 2·2·5 = 2^2·5^1 28 = 2·2·7 = 2^2·7^1 Выбираем все простые делители (множители) с наибольшими степенями, перемножаем их и находим НОК: НОК = 2^2·4^1·5^1·7^1 = 4·4·5·7 = 560. НОК(16, 20, 28) = 560. Таким образом, в итоге расчета получилось число 560. Оно является наименьшим общим кратным, то есть делится на каждое из трёх чисел без остатка. Матве­й628 [90.1K] 9 лет назад  Чтобы найти наименьшее общее кратное, нужно выполнить последовательно несколько простых действий. Рассмотрим это на примере двух чисел: 8 и 12 Разлагаем оба числа на простые множители: 8=2*2*2 и 12=3*2*2 Сокращаем одинаковые множители у одного из чисел. В нашем случае совпадают 2*2, сократим их для числа 12, тогда у 12 останется один множитель: 3. Находим произведение всех оставшихся множителей: 2*2*2*3=24 Проверяя, убеждаемся, что 24 делится и на 8 и на 12, причем это наименьшее натуральное число, которое делится на каждое из этих чисел. Вот мы и нашли наименьшее общее кратное. ирише­нька [41.2K] 8 лет назад  Попробую объяснить на примере цифр 6 и 8. Наименьшее общее кратное – это число, которое можно разделить на эти числа(в нашем случае 6 и 8) и остатка не будет. Итак, начинаем умножать сначала 6 на 1, 2, 3 и т. д и 8 на 1, 2, 3 и т. д. Получается: Умножаем на 6 – 6-12-18-24-30-36-42-48-54-60 Умножаем не 8 – 8-16-24-32-40-48…. Как видим, и там и там есть 48, следовательно у чисел 6 и 8 наименьшее общее кратное – 48. ЯнаМа­рина [75.6K] 8 лет назад  Наименьшее общее кратное число – это такая цифра, которая разделится на несколько предложенных чисел без остатка. Для того, чтобы такую цифру высчитать, надо взять каждое число и разложить его на простые множители. Те цифры, которые совпадают, убираем. Оставляет всех по одной, перемножаем их между собой по очереди и получаем искомое – наименьшее общее кратное. Например у нас есть числа 3 и 5 и нам надо найти НОК(наименьшее общее кратное). Нам надо умножать и тройку и пятёрку на все числа начиная с 1 2 3 … и т д пока мы не увидим одинаковое число и там и там. Множим тройку и получаем: 3, 6, 9, 12, 15 Множим пятёрку и получаем: 5, 10, 15 НОК = 15 Infil­trato­r [100K] 11 лет назад  Нужно найти каждый множитель каждого из двух чисел, у которых находим наименьшее общее кратное, а потом перемножить друг на друга множители, которые совпали у первого и второго числа. Результатом произведения будет искомое кратное. Azama­tik [55.3K] 5 лет назад  Первым делом нужно разложить числа (для которых ищем наименьшее общее кратное) на множители. После чего остается домножить одно из чисел на тот множитель или на те множители, которые не входят в его разложение, но при этом входят в разложение других чисел (другого числа). Итак, пример: нужно найти наименьшее общее кратное чисел 24 и 36. Разложим на множители оба числа: 24 это 3 х 4 х 2; 36 это 3 х 4 х 3. Сокращаем одинаковые множители и остается одна 3. Умножаем 3 х 4 х 2 х 3 и получаем 72. Ответ: 72 это НОК для чисел 24 и 36. Знаете ответ?