Как найти наименьшее общее кратное знаменателей дробей

Как найти наименьшее общее кратное знаменателей дробей


Загрузить PDF


Загрузить PDF

Для сложения или вычитания дробей с разными знаменателями (числа, стоящие под дробной чертой) сначала необходимо найти их наименьший общий знаменатель (НОЗ). Таким числом будет наименьшее кратное, которое встречается в списке кратных каждого знаменателя, то есть число, делящееся нацело на каждый знаменатель.[1]
 Также вы можете вычислить наименьшее общее кратное (НОК) двух или более знаменателей. В любом случае речь идет о целых числах, методы нахождения которых весьма схожи. Определив НОЗ, вы сможете привести дроби к общему знаменателю, что в свою очередь позволит вам складывать и вычитать их.

  1. Изображение с названием Find the Least Common Denominator Step 1

    1

    Перечислите кратные каждого знаменателя. Составьте список из нескольких кратных для каждого знаменателя в уравнении. Каждый список должен состоять из произведения знаменателя на 1, 2, 3, 4 и так далее.

    • Пример: 1/2 + 1/3 + 1/5
    • Кратные 2: 2 * 1 = 2; 2 * 2 = 4; 2 * 3 = 6; 2 * 4 = 8; 2 * 5 = 10; 2 * 6 = 12; 2 * 7 = 14; и так далее.
    • Кратные 3: 3 * 1 = 3; 3 * 2 = 6; 3 *3 = 9; 3 * 4 = 12; 3 * 5 = 15; 3 * 6 = 18; 3 * 7 = 21; и так далее.
    • Кратные 5: 5 * 1 = 5; 5 * 2 = 10; 5 * 3 = 15; 5 * 4 = 20; 5 * 5 = 25; 5 * 6 = 30; 5 * 7 = 35; и так далее.

  2. Изображение с названием Find the Least Common Denominator Step 2

    2

    Определите наименьшее общее кратное. Просмотрите каждый список и отметьте любые кратные числа, которые являются общими для всех знаменателей. После выявления общих кратных определите наименьший знаменатель.

    • Обратите внимание, что если общий знаменатель не найден, возможно, потребуется продолжить выписывать кратные до тех пор, пока не появится общее кратное число.
    • Лучше (и легче) пользоваться этим методом в том случае, когда в знаменателях стоят небольшие числа.
    • В нашем примере общим кратным всех знаменателей является число 30: 2 * 15 = 30; 3 * 10 = 30; 5 * 6 = 30
    • НОЗ = 30

  3. Изображение с названием Find the Least Common Denominator Step 3

    3

    Перепишите исходное уравнение. Для того чтобы привести дроби к общему знаменателю, при этом не изменив их значения, умножьте каждый числитель (число, стоящее над дробной чертой) на число, равное частному от деления НОЗ на соответствующий знаменатель.

    • Пример: (15/15) * (1/2); (10/10) * (1/3); (6/6) * (1/5)
    • Новое уравнение: 15/30 + 10/30 + 6/30

  4. Изображение с названием Find the Least Common Denominator Step 4

    4

    Решите полученное уравнение. После нахождения НОЗ и изменения соответствующих дробей, просто решите полученное уравнение. Не забудьте упростить полученный ответ (если это возможно).

    • Пример: 15/30 + 10/30 + 6/30 = 31/30 = 1 1/30

    Реклама

  1. Изображение с названием Find the Least Common Denominator Step 5

    1

    Перечислите делители каждого знаменателя. Делитель – это целое число, которое делит нацело данное число.[4]
     Например, делителями числа 6 являются числа 6, 3, 2, 1. Делителем любого числа является 1, потому что любое число делится на единицу.

    • Пример: 3/8 + 5/12
    • Делители 8: 1, 2, 4, 8
    • Делители 12: 1, 2, 3, 4, 6, 12

  2. Изображение с названием Find the Least Common Denominator Step 6

    2

    Найдите наибольший общий делитель (НОД) обоих знаменателей. Перечислив делители каждого знаменателя, отметьте все общие делители. Самый большой общий делитель является наибольшим общим делителем, который понадобится вам для решения задачи.

    • В нашем примере общими делителями для знаменателей 8 и 12 являются числа 1, 2, 4.
    • НОД = 4.

  3. Изображение с названием Find the Least Common Denominator Step 7

    3

    Перемножьте знаменатели между собой. Если вы хотите использовать НОД для решения задачи, сначала перемножьте знаменатели между собой.

    • Пример: 8 * 12 = 96

  4. Изображение с названием Find the Least Common Denominator Step 8

    4

    Разделите полученное значение на НОД. Получив результат перемножения знаменателей, разделите его на вычисленный вами НОД. Полученное число будет наименьшим общим знаменателем (НОЗ).

    • Пример: 96 / 4 = 24

  5. Изображение с названием Find the Least Common Denominator Step 9

    5

    Разделите НОЗ на исходный знаменатель. Для вычисления множителя, который требуется для приведения дробей к общему знаменателю, разделите найденный вами НОЗ на исходный знаменатель. Умножьте числитель и знаменатель каждой дроби на этот множитель. Вы получите дроби с общим знаменателем.

    • Пример: 24 / 8 = 3; 24 / 12 = 2
    • (3/3) * (3/8) = 9/24; (2/2) * (5/12) = 10/24
    • 9/24 + 10/24

  6. Изображение с названием Find the Least Common Denominator Step 10

    6

    Решите полученное уравнение. НОЗ найден; теперь вы можете сложить или вычесть дроби. Не забудьте упростить полученный ответ (если это возможно).

    • Пример: 9/24 + 10/24 = 19/24

    Реклама

  1. Изображение с названием Find the Least Common Denominator Step 11

    1

    Разложите каждый знаменатель на простые множители. Разложите каждый знаменатель на простые множители, то есть простые числа, которые при перемножении дают исходный знаменатель. Напомним, что простые множители – это числа, которые делятся только на 1 или самих себя.[6]

    • Пример: 1/4 + 1/5 + 1/12
    • Простые множители 4: 2 * 2
    • Простые множители 5: 5
    • Простые множители 12: 2 * 2 * 3

  2. Изображение с названием Find the Least Common Denominator Step 12

    2

    Подсчитайте число раз каждый простой множитель есть у каждого знаменателя. То есть определите, сколько раз каждый простой множитель появляется в списке множителей каждого знаменателя.

    • Пример: Есть две 2 для знаменателя 4; нуль 2 для 5; две 2 для 12
    • Есть нуль 3 для 4 и 5; одна 3 для 12
    • Есть нуль 5 для 4 и 12; одна 5 для 5

  3. Изображение с названием Find the Least Common Denominator Step 13

    3

    Возьмите только наибольшее число раз для каждого простого множителя. Определите наибольшее число раз наличия каждого простого множителя в любом знаменателе.

    • Например: наибольшее число раз для множителя 2 – 2 раза; для 3 – 1 раз; для 5 – 1 раз.

  4. Изображение с названием Find the Least Common Denominator Step 14

    4

    Запишите по порядку найденные в предыдущем шаге простые множители. Не записывайте число раз наличия каждого простого множителя во всех исходных знаменателях – делайте это с учетом наибольшего числа раз (как описано в предыдущем шаге).

    • Пример: 2, 2, 3, 5

  5. Изображение с названием Find the Least Common Denominator Step 15

    5

    Перемножьте эти числа. Результат произведения этих чисел равен НОЗ.

    • Пример: 2 * 2 * 3 * 5 = 60
    • НОЗ = 60

  6. Изображение с названием Find the Least Common Denominator Step 16

    6

    Разделите НОЗ на исходный знаменатель. Для вычисления множителя, который требуется для приведения дробей к общему знаменателю, разделите найденный вами НОЗ на исходный знаменатель. Умножьте числитель и знаменатель каждой дроби на этот множитель. Вы получите дроби с общим знаменателем.

    • Пример: 60/4 = 15; 60/5 = 12; 60/12 = 5
    • 15 * (1/4) = 15/60; 12 * (1/5) = 12/60; 5 * (1/12) = 5/60
    • 15/60 + 12/60 + 5/60

  7. Изображение с названием Find the Least Common Denominator Step 17

    7

    Решите полученное уравнение. НОЗ найден; теперь вы можете сложить или вычесть дроби. Не забудьте упростить полученный ответ (если это возможно).

    • Пример: 15/60 + 12/60 + 5/60 = 32/60 = 8/15

    Реклама

  1. Изображение с названием Find the Least Common Denominator Step 18

    1

    Преобразуйте каждое смешанное число в неправильную дробь. Для этого умножьте целую часть смешанного числа на знаменатель и сложите с числителем – это будет числитель неправильной дроби. Целое число тоже превратите в дробь (просто поставьте 1 в знаменателе).

    • Пример: 8 + 2 1/4 + 2/3
    • 8 = 8/1
    • 2 1/4, 2 * 4 + 1 = 8 + 1 = 9; 9/4
    • Переписанное уравнение: 8/1 + 9/4 + 2/3

  2. Изображение с названием Find the Least Common Denominator Step 19

    2

    Найти наименьший общий знаменатель. Вычислите НОЗ любым способом, описанным в предыдущих разделах. Для этого примера мы будем использовать метод “перечисление кратных”, в котором выписываются кратные каждого знаменателя и на их основе вычисляется НОЗ.

    • Обратите внимание, что вам не нужно перечислять кратные для 1, так как любое число, умноженное на 1, равно самому себе; иными словами, каждое число является кратным 1.
    • Пример: 4 * 1 = 4; 4 * 2 = 8; 4 * 3 = 12; 4 * 4 = 16; т.д.
    • 3 * 1 = 3; 3 * 2 = 6; 3 * 3 = 9; 3 * 4 = 12; т.д.
    • НОЗ = 12

  3. Изображение с названием Find the Least Common Denominator Step 20

    3

    Перепишите исходное уравнение. Числители и знаменатели исходных дробей умножьте на число, равное частному от деления НОЗ на соответствующий знаменатель.

    • Например: (12/12) * (8/1) = 96/12; (3/3) * (9/4) = 27/12; (4/4) * (2/3) = 8/12
    • 96/12 + 27/12 + 8/12

  4. Изображение с названием Find the Least Common Denominator Step 21

    4

    Решите уравнение. НОЗ найден; теперь вы можете сложить или вычесть дроби. Не забудьте упростить полученный ответ (если это возможно).

    • Пример: 96/12 + 27/12 + 8/12 = 131/12 = 10 11/12

    Реклама

Что вам понадобится

  • Карандаш
  • Бумага
  • Калькулятор (по желанию)

Об этой статье

Эту страницу просматривали 222 786 раз.

Была ли эта статья полезной?

Источник

Наименьший общий знаменатель для двух или более чем двух дробей дробей равен наименьшему общему кратному знаменателей этих дробей.

Таким образом, нахождение наименьшего общего знаменателя для двух или нескольких дробей сводится к нахождению наименьшего общего кратного их знаменателей.

Чтобы найти наименьшее общее кратное (НОК) двух или нескольких чисел, необходимо:

1) разложить все эти числа на простые множители (выполнить каноническое разложение);

2) для нахождения НОК — выписать все множители, которые встречаются в каноническом разложении хотя бы одного из исходных чисел, причём каждый простой множитель следует взять с наибольшим встречающимся показателем;

3) вычислить произведение множителей, выписанных в пункте 2 (с учётом их степеней. Возведение в степень имеет приоритет перед умножением.)

Приведу пример. Нам нужно привести к наименьшему общему знаменателю дроби 11/120 и 13/126.

Для этого нам нужно найти наименьшее общее кратное знаменателей этих дробей.

Знаменатели этих дробей равны 120 и 126.

Выполним каноническое разложение этих чисел:

120 = 2^3 * 3 * 5;

126 = 2 * 3^2 * 7.

Находим НОК этих чисел. Для этого нужно выписать все простые множители, которые вообще встречаются в разложении хотя бы одного из этих чисел. В данном случае это множители 2, 3, 5 и 7. Причём каждый из них нужно взять с наибольшим показателем: двойку берём с показателем 3, тройку с показателем 2, пятёрку с показателем 1 и семёрку также с показателем 1.

Итак:

НОК (120, 126) = 2^3 * 3^2 * 5 * 7 = 8 * 9 * 5 * 7 = 2520.

Общий знаменатель равен 2520.

Чтобы привести две или несколько дробей к наименьшему общему знаменателю, нужно:

1) найти этот общий знаменатель, пользуясь вышеприведённым алгоритмом нахождения наименьшего общего знаменателя;

2) найти дополнительные множители для каждой дроби. Для этого найденный общий знаменатель необходимо разделить на знаменатели каждой из приведённых дробей (деление производится по отдельности);

3) помножить числители каждой из исходных дробей на дополнительные множители, найденные в пункте 2.

Например, нужно привести дроби 11/120 и 13/126 к наименьшему общему знаменателю.

1) Находим наименьший общий знаменатель. Он равен 2520.

2) Находим дополнительные множители.

Для первой дроби: 2520 : 120 = 21.

Для второй дроби: 2520 : 126 = 20.

3) Домножаем числители дробей на дополнительные множители.

Для первой дроби: 11 * 21 = 231.

Для второй дроби: 13 * 20 = 260.

Итак, дроби 11/120 и 13/126 после приведения к наименьшему общему знаменателю стали равными 231/2520 и 260/2520.

Несколько слов по поводу нахождения общего знаменателя у дробей, знаменатели которых содержат буквы (переменные или константы).

Если знаменатели двух или нескольких дробей представляют собой многочлены, то для нахождения простейшего общего знаменателя достаточно разложить все знаменатели на одночлены и затем взять произведение всех одночленов, которые встречаются в разложении хотя бы одного знаменателя, при этом взяв каждый одночлен в наибольшей встречающейся степени.

Если же знаменатели выражены одночленами — простейшим общим знаменателем будет одночлен, коэффициент которого равен наименьшему общему кратному коэффициентов знаменателей-одночленов, а далее следуют все буквы, которые встречаются хотя бы в одном из знаменателей, причём каждую букву необходимо взять с наибольшим встречающимся показателем.

Например, для знаменателей 8a^3c^7d и 12ab^5c^4d^2e простейшим общим знаменателем будет 24a^3b^5c^7d^2e.

Ну а по поводу наибольшего общего знаменателя — не шутка ли это?

Наибольшего общего знаменателя не существует по той причине, что ряд натуральных чисел бесконечен.

Источник

Для того, чтобы находить общий знаменатель
при
сложении
и
вычитании дробей с разными
знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).

Кратное числу «a» — это число, которое
само делится на число «a» без остатка.

Числа кратные 8
(то есть, эти числа разделятся на 8 без остатка):
это числа 16, 24, 32 …

Кратные 9: 18, 27, 36, 45 …

Чисел, кратных данному числу a бесконечно много, в отличии от делителей
этого же числа. Делителей —
конечное количество.

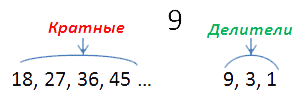
кратные и делители числа

Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.

Запомните!
!

Наименьшим общим кратным (НОК) двух и более натуральных
чисел называется наименьшее натуральное число, которое само
делится нацело на каждое из этих чисел.

Как найти НОК

НОК можно найти и записать двумя способами.

Первый способ нахождения НОК

Данный способ обычно применяется для небольших чисел.

  1. Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое
    для обоих чисел.
  2. Кратное числа «a»
    обозначаем большой буквой «К».

    К (a) = {…, …}

Пример. Найти НОК 6 и 8.

К (6) = {12, 18, 24, 30, …}

К (8) = {8, 16, 24, 32, …}

НОК (6, 8) = 24

Второй способ нахождения НОК

Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.

  1. Разложить данные числа на простые множители.
    Подробнее правила разложения на
    простые множители вы можете прочитать в теме
    как найти наибольший общий делитель (НОД).
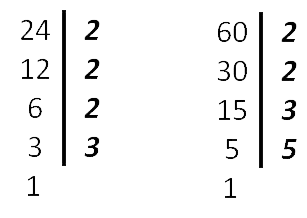
    разложение чисел на простые множители
  2. Выписать в строчку множители, входящие в разложение
    самого большого из чисел, а под ним —
    разложение остальных чисел.

    Запомните!
    !

    Количество одинаковых множителей в разложениях чисел может быть разное.

    60 = 2 · 2 · 3 · 5

    24 = 2 · 2 · 2 · 3

  3. Подчеркнуть в разложении
    меньшего числа (меньших чисел) множители,
    которые не вошли в разложение бóльшего числа
    (в нашем примере это 2) и добавить эти множители в разложение бóльшего числа.

    НОК (24, 60) = 2 · 2 · 3 · 5 · 2
  4. Полученное произведение записать в ответ.

    Ответ: НОК (24, 60) = 120

Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24).

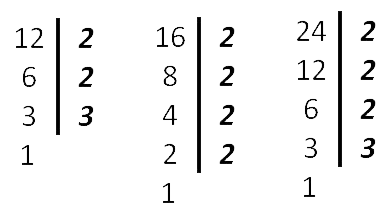
пример нахождения наименьшего общего кратного (НОК)
24 = 2 · 2 · 2 · 3

16 = 2 · 2 · 2 · 2

12 = 2 · 2 · 3

Как видим из разложения чисел, все множители 12 вошли в
разложение 24
(самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из
разложения числа 16.

НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48

Ответ: НОК (12, 16, 24) = 48

Особые случаи нахождения НОК

  1. Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.

    Например, НОК (60, 15) = 60

  2. Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее
    кратное равно произведению этих чисел.

    Пример.

    НОК (8, 9) = 72

Ваши комментарии

Важно!
Галка

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Пришелец пожимает плечами

Оставить комментарий:

5 сентября 2020 в 15:37

Елена Елена
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Елена Елена
Профиль
Благодарили: 0

Сообщений: 1

НОК(360,102)

0
Спасибоthanks
Ответить

6 сентября 2020 в 13:42
Ответ для Елена Елена

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60


360 = 23 · 32 · 5;    102 = 2 · 3 · 17.
НОК(360; 102) = 23 · 32 · 5 · 17  = …

0
Спасибоthanks
Ответить

30 мая 2018 в 17:34

Тамара Татарникова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Тамара Татарникова
Профиль
Благодарили: 0

Сообщений: 1

Найдите четырёхзначное число, которое кратно 24, а произведение цифр этого числа равно 16, в ответ дайте какое-нибудь одно число.
Я написала 1242, но 1242 при делении на 24 дает в ответе 51,75 будет ли это верным ответом?

0
Спасибоthanks
Ответить

3 июня 2018 в 1:58
Ответ для Тамара Татарникова

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60


1128  1224  8112

0
Спасибоthanks
Ответить

29 ноября 2016 в 14:47

Анвар Тынайбеков
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Анвар Тынайбеков
Профиль
Благодарили: 0

Сообщений: 1

НОК(344и170)=

0
Спасибоthanks
Ответить

2 декабря 2016 в 8:23
Ответ для Анвар Тынайбеков

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

1
Спасибоthanks
Ответить

15 февраля 2016 в 19:02

Кирилл Журавлёв
(^-^)
Профиль
Благодарили: 1

Сообщений: 3

(^-^)
Кирилл Журавлёв
Профиль
Благодарили: 1

Сообщений: 3

число 123 454 321 делится на 11 111. найдите нок этих чисел 

1
Спасибоthanks
Ответить

15 февраля 2016 в 19:08
Ответ для Кирилл Журавлёв

Кирилл Журавлёв
(^-^)
Профиль
Благодарили: 1

Сообщений: 3

(^-^)
Кирилл Журавлёв
Профиль
Благодарили: 1

Сообщений: 3


12132211

0
Спасибоthanks
Ответить

19 сентября 2016 в 12:55
Ответ для Кирилл Журавлёв

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197


Здесь подробно описано нахождение НОК.

А в супер-решателе можно себя проверить.

0
Спасибоthanks
Ответить

15 февраля 2016 в 18:51

Кирилл Журавлёв
(^-^)
Профиль
Благодарили: 1

Сообщений: 3

(^-^)
Кирилл Журавлёв
Профиль
Благодарили: 1

Сообщений: 3

ЧИСЛО 123 454 321 ДЕЛИТСЯ 11 111. НАЙДИТЕ НОК ЭТИХ ЧИСЕЛ НЕ ВЫПОЛНЯЯ РАЗЛОЖЕНИЯ ЧИСЕЛ НА ПРОСТЫЕ МНОЖИТЕЛИ

0
Спасибоthanks
Ответить

19 сентября 2016 в 12:56
Ответ для Кирилл Журавлёв

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

0
Спасибоthanks
Ответить

27 января 2016 в 18:15

Lera Kuchinskaya
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Lera Kuchinskaya
Профиль
Благодарили: 0

Сообщений: 1

НОК 100 150 250cry

0
Спасибоthanks
Ответить

27 января 2016 в 22:36
Ответ для Lera Kuchinskaya

Виктория Казимирова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Виктория Казимирова
Профиль
Благодарили: 0

Сообщений: 1


А что за цифры!!!? 

0
Спасибоthanks
Ответить

28 января 2016 в 16:00
Ответ для Lera Kuchinskaya

Anton Wuckert
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Anton Wuckert
Профиль
Благодарили: 0

Сообщений: 1


НОК = 1500

0
Спасибоthanks
Ответить

19 сентября 2016 в 11:42
Ответ для Lera Kuchinskaya

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197


Для решения можно воспользоваться решателем на сайте.

0
Спасибоthanks
Ответить

22 января 2016 в 13:46

Андрей Алексеев
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Андрей Алексеев
Профиль
Благодарили: 0

Сообщений: 1

числа 4,5,6,7,10,12,15,16,20,50, которые являются делителями 24 и кратными 2

0
Спасибоthanks
Ответить

23 января 2016 в 13:33
Ответ для Андрей Алексеев

Александра Сирота
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Александра Сирота
Профиль
Благодарили: 0

Сообщений: 2


ОТВЕТ: 4 и 12

0
Спасибоthanks
Ответить

24 января 2016 в 13:41
Ответ для Андрей Алексеев

Инна Шабрашина
(^-^)
Профиль
Благодарили: 0

Сообщений: 5

(^-^)
Инна Шабрашина
Профиль
Благодарили: 0

Сообщений: 5


6 ,2,  12

0
Спасибоthanks
Ответить

25 января 2016 в 19:52
Ответ для Андрей Алексеев

Нелия Ахмедова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Нелия Ахмедова
Профиль
Благодарили: 0

Сообщений: 1


6,12.

0
Спасибоthanks
Ответить

19 сентября 2016 в 10:59
Ответ для Андрей Алексеев

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197


Чтобы не запутаться, необходимо каждое из чисел проверить на оба условия: 
1) 4 — 24/4=6 — делитель 24. 4/2=2 — кратно 2.
2) 5 — 24/5=не делится без остатка — не делитель. 5/2 — не делится без остатка — не кратно 2.
И так далее.
Ответ: 4,6,12.

0
Спасибоthanks
Ответить

23 декабря 2015 в 17:00

Евгений Мухамедшин
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Евгений Мухамедшин
Профиль
Благодарили: 0

Сообщений: 1

1) (4/15+5/8)-3/5

2)  (1/5+13/16)-9/20

0
Спасибоthanks
Ответить

19 сентября 2016 в 10:01
Ответ для Евгений Мухамедшин

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197


Для нахождения НОК можно воспользоваться супер-решателем. Раскрываем скобки и приводим к общему знаменателю.
1) ===0
2) ===   

0
Спасибоthanks
Ответить

17 ноября 2015 в 6:29

Светлана Каблучко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Светлана Каблучко
Профиль
Благодарили: 0

Сообщений: 1

запишите числа удовлетворяющие двойное неравенство 354<х<361 если известно что они кратны 2,5,10

0
Спасибоthanks
Ответить

24 ноября 2015 в 17:56
Ответ для Светлана Каблучко

Тима Клюев
(^-^)
Профиль
Благодарили: 0

Сообщений: 8

(^-^)
Тима Клюев
Профиль
Благодарили: 0

Сообщений: 8


360

0
Спасибоthanks
Ответить

Источник

Добавить комментарий