Формулировка задания: Укажите наименьшее основание системы счисления, в которой запись числа K-значна.
Задание входит в ЕГЭ по информатике для 11 класса под номером 16 (Кодирование чисел. Системы счисления).
Рассмотрим, как решаются подобные задания на примере.
Пример задания:
Укажите наименьшее основание системы счисления, в которой запись числа 70 трехзначна.
Решение:
Решим задачу методом подбора: будем перебирать основания системы счисления, начиная с наименьшего (2), и переводить число 70 в каждую из этих систем счисления:
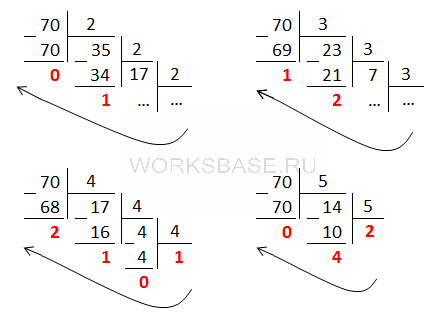
В двоичной, троичной и четвертичной системах счисления в числе больше 3 цифр. А в системе счисления с основанием 5 их ровно 3.
Таким образом, наименьшее основание системы счисления равно 5.
Ответ: 5
Поделитесь статьей с одноклассниками «Укажите наименьшее основание системы счисления, в которой запись – как решать».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
14. Системы счисления (сложно)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Решите уравнение: (46_{10}=56_x)
Переведем 56 в десятичную систему счисления: (56_x=6cdot x^0+5cdot x^1=6+5x)
Составим линейное уравнение, решим его:
(46=6+5x)
(40=5x)
(x=8)
Для перепроверки сделаем обратный перевод: (56_8=6cdot8^0+5cdot8^1=46)
Ответ: 8
Решите уравнение: (17_{10}=32_x)
Ответ запишите в двоичной системе счисления.
Переведем 32 в десятичную систему счисления: (32_x=2cdot x^0+3cdot x^1=2+3x)
Составим линейное уравнение, решим его:
(17=2+3x)
(15=3x)
(x=5)
Теперь переведем искомое основание в двоичную систему счисления: (5_{10}=1cdot2^2+0cdot2^1+1cdot2^0=101_2)
Ответ: 101
Решите уравнение: (125_8+10_3=323_x)
Ответ запишите в троичной системе счисления.
Для удобства переведем все числа в десятичную систему счисления:
(125_8=5cdot8^0+2cdot8^1+1cdot8^2=5cdot1+2cdot8+1cdot64=5+16+64=85_{10})
(10_3=0cdot3^0+1cdot3^1=0cdot1+1cdot3=3_{10})
(323_x=3cdot x^0+2cdot x^1+3cdot x^2=3cdot1+2cdot x+3cdot x^2=(3+2x+3x^2)_{10})
Теперь, когда все числа находятся в одной системе счисления, можем составить квадратное уранение:
(85+3=3+2x+3x^2)
(3x^2+2x-85=0)
(D=2^2-4cdot3cdot(-85)=4+12cdot85=1024); (sqrt D=32)
[left[
begin{gathered}
x=frac{-2+32}{2cdot3}=frac{30}{6}=5 hfill
\
x=frac{-2-32}{2cdot3}=-frac{34}{6}<0, text{основание системы счисления не может быть отрицательным}\
end{gathered}
right.] Переведем искомое основание в троичную систему счисления: (5_{10}=1cdot3^1+2cdot3^0=12_3).
Ответ: 12
Найдите наименьшее основание системы счисления, в которой десятичное число 79 имеет четырехзначную запись.
Если запись числа четырехзначна, максимальное значение числа равно (x^4-1), где переменная – основание системы счисления. Это можно увидеть на примере с десятичной системой счисления. Максимальное четырехзначное число: (10^4-1=10000-1=9999), максимальное трехзначное число: (10^3-1=1000-1=999). Аналогично перебираем другие системы счисления, удовлетворяющие условию задачи:
Двоичная: (2^4-1=15), слишком мало, запись числа 79 будет состоять более, чем из четырех цифр.
Троичная: (3^4-1=80). Значит, искомое значение – 3. Для проверки переведем 79 в троичную систему счисления: (79_{10}=2cdot3^3+2cdot3^2+2cdot3^1+1cdot3^0=2221_3).
Ответ: 3
Найдите наименьшее основание системы счисления, в которой десятичное число 91 имеет ровно три значащих разряда.
Если запись числа имеет ровно три значащих разряда, то запись числа трехзначна (состоит из трех цифр, не равных нулю). Если запись числа трехзначна, то максимальное значение числа равно (x^3-1), где переменная – основание системы счисления. Это можно увидеть на примере с десятичной системой счисления. Максимальное четырехзначное число: (10^3-1=1000-1=999), максимальное двузначное число: (10^2-1=100-1=99). Аналогично перебираем другие системы счисления, удовлетворяющие условию задачи:
Двоичная: (2^3-1=7), слишком мало, запись числа 91 будет состоять более, чем из 3-х цифр.
Троичная: (3^3-1=26), слишком мало, запись числа 91 будет состоять более, чем из 3-х цифр.
Четверичная: (4^3-1=63), слишком мало, запись числа 91 будет состоять более, чем из 3-х цифр.
Пятеричная: (5^3-1=124). Значит, искомое основание – 5. Для проверки переведем (91_{10}=3cdot5^2+3cdot5^1+1cdot5^0=331_5)
Ответ: 5
Решите уравнение: (10_{10}=101_x)
Переведем 101 в десятичную систему счисления: (101_x=1cdot x^0+0cdot x^1+1cdot x^2=1+x^2)
Теперь подставим в наше уравнение вместо (101_x) полученное выражение и решим квадратное уравнение:
(10=1+x^2)
(9=x^2)
(x=pm3)
Отрицательный корень нам не подходит, т.к. основание системы счисления не может быть отрицательным. Значит, искомое основание равно 3.
Для перепроверки сделаем обратный перевод: (101_3=1cdot3^0+0cdot3^1+1cdot 3^2=1+0+9=10_{10})
Ответ: 3
Решите уравнение: (17_{10}=101_x)
Переведем 101 в десятичную систему счисления: (101_x=1cdot x^0+0cdot x^1+1cdot x^2=1+x^2)
Теперь подставим в наше уравнение вместо (101_x) полученное выражение и решим квадратное уравнение:
(17=1+x^2)
(16=x^2)
(x=pm4)
Отрицательный корень нам не подходит, т.к. основание системы счисления не может быть отрицательным. Значит, искомое основание равно 4.
Для перепроверки сделаем обратный перевод: (101_4=1cdot4^0+0cdot4^1+1cdot 4^2=1+0+16=17_{10})
Ответ: 4

УСТАЛ? Просто отдохни

Всем привет! Нужно решить задачку на питоне. Важно, что списки использовать нельзя, функции тоже. “Половину” я уже сделал, определил основания обоих чисел. Дальше не могу без списков и функций. Вставляю свой код
| Python | ||
|
Тут answ – основание первого числа, answ1 – второго числа. Почти на 100 процентов уверен в том, что работает))) Помогите, пожалуйста!
Условие задачи:
Не всякое число может являться записью в данной системе счисления. Например, 123 не может быть числом ни в двоичной, ни в троичной системе. Наименьшее основание системы счисления, в которой может быть записано это число – четыре.
Напишите программу, которая это и будет определять.
Вводятся два числа, записанных в разных, но неизвестных системах счисления. Для каждого из них нужно найти минимальное основание системы счисления, в которой это число может быть записано. Затем число в меньшей системе перевести в систему с большим основанием.
Гарантируется, что основания разные и не превышают 10.
Формат ввода
Два целых положительных числа.
Формат вывода
Целое число.
Пример 1
Ввод Вывод
123
214
102
Пример 2
Ввод Вывод
192
10010
18
Примечания
В задаче нельзя использовать списки, методы и функции.
Заранее спасибо.
Ответ – 7.
Максимальная цифра 6, значит, в системе должны существовать цифры 0 1 2 3 4 5 6.
Шестеричная система не подходит, нету 6 (в меньших, разумеется, тоже нету). А вот семеричная подходит! Там как раз цифры от 0 до 6.
Итак, мы доказали, что 7-чная система подходит, а меньшие нет. Поэтому 7 – наименьшее основание.
Формула для любого числа такова: находим максимальную цифру + 1 (работает по тому же принципу)
4,1 K
Комментировать ответ…Комментировать…
поэт, музыкант, математик, инженер, программист, котельщик, электрик, сантехник · 31 окт 2021 ·
Могу предложить троичную систему счисления, в которой есть три цифры для записи чисел: 2, 3 и 6. В троичной системе с символами 0, 1 и 2 это было бы 102, а в десятичной число 11.
166
Комментировать ответ…Комментировать…
В данном случае минимальное основание – 7.
Алгоритм прост – находим в числе “старшую” цифру, в вашем случае это 6 и прибавляем 1 (за счет нуля).
Аналогично, минимальное основание для 110101 – 2
46475 – 8
110А345 – 11.
167
Комментировать ответ…Комментировать…
математик, патриот России, духовный последователь Циолковского · 31 окт 2021
В данном случае это основание есть 7-минимальная система счисления здесь семиричная. Это следует из того, что мы первые 6 символов (цифр) для обозначения каких угодно предметных чисел задаём такими: 0,1,2,3,4,5,6 (в порядке возрастания-от меньшего к большему). Мы видим, что наибольшая из упомянутых цифр числа 326 суть 6, значит, подобно тому как мы в десятичной системе… Читать далее
1,1 K
Комментировать ответ…Комментировать…
О сообществе
Переведём все строки-числа в массивы со значениями их цифр. Запишем их задом-наперед. Более короткие дополним нулями:
A: 1A -> [10, 1]
B: 2 -> [ 2, 0]
C: 20 -> [ 0, 2]
Пройдемся слева направо имитируя сложение в столбик. Рассмотрим сумму младших разрядов: если бы переноса не возникло, то A[0] + B[0] == C[0]. Это не так (10 + 2 != 0). Значит есть перенос и A[0] + B[0] == base + C[0]. Можно вычислить основание системы счисления.
В следующем разряде нужно учесть пришедший перенос: A[1] + B[1] + carry == C[1]. Равенство выполнено, проверять основание не надо.
Продвигаясь по разрядам выполняем сложение в столбик. При каждом переносе проверяем основание – все переносы должны дать один результат. Кроме этого основание должно быть больше всех цифр в во всех трёх числах.
def read_number(s):
alphabet = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ'
return list(map(alphabet.index, reversed(s)))
def align(lists):
max_length = max(map(len, lists))
for l in lists:
l.extend([0] * (max_length - len(l)))
def determine_base(a, b, c):
align((a, b, c))
max_digit = max(a + b + c)
base = None
carry = 0
for ai, bi, ci in zip(a, b, c):
s = ai + bi + carry
if s < ci:
return -1
if s > ci:
if base is None:
base = s - ci
if base <= max_digit:
return -1
if s - ci != base:
return -1
carry = 1
else:
carry = 0
if carry != 0:
return -1
if base is None:
return max_digit + 1
return base
def main():
a, b, c = tuple(map(read_number, input().split()))
print(determine_base(a, b, c))
main()
