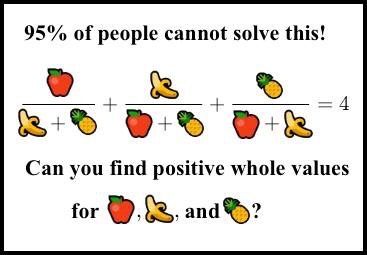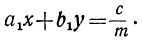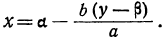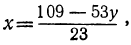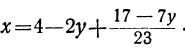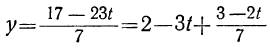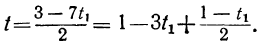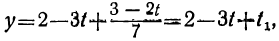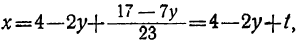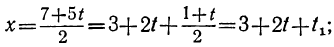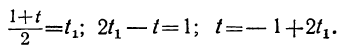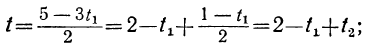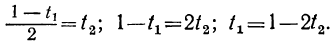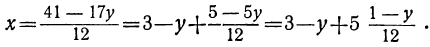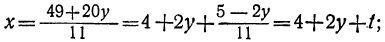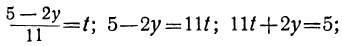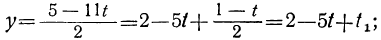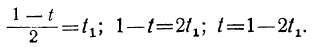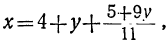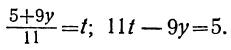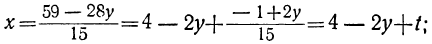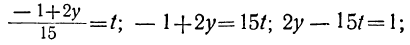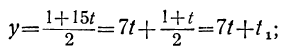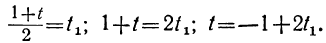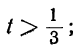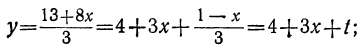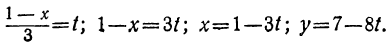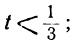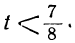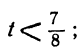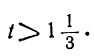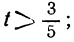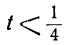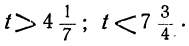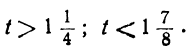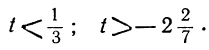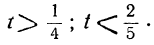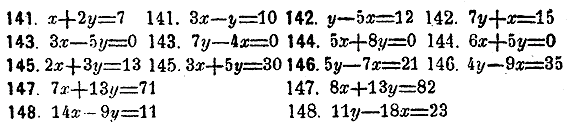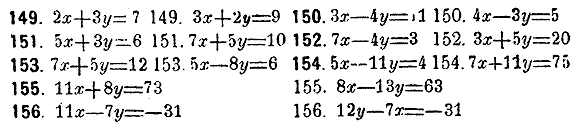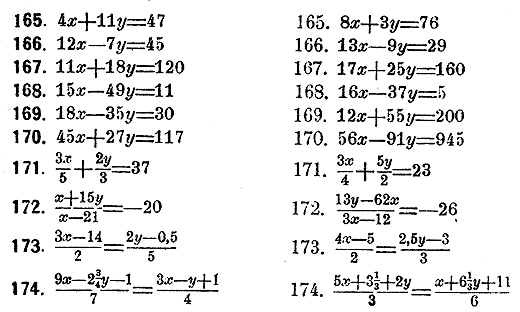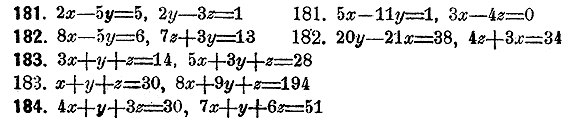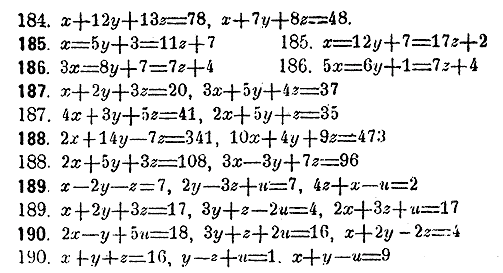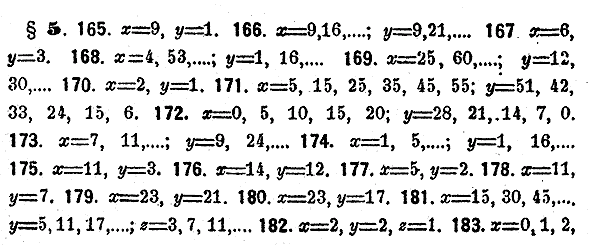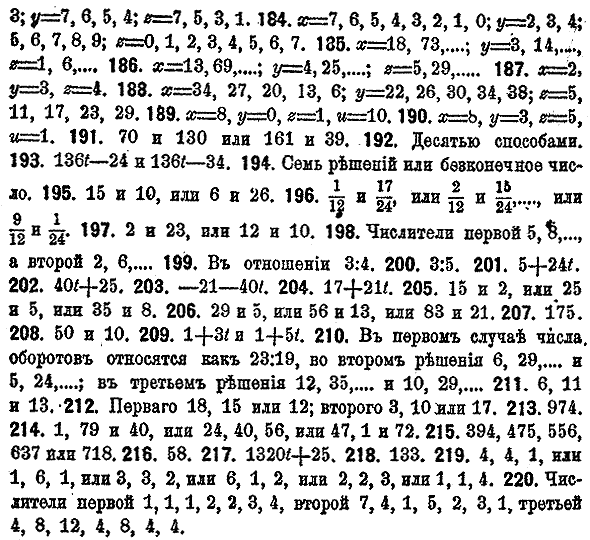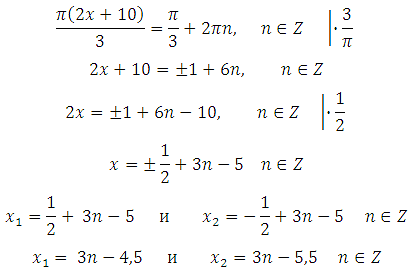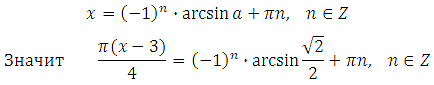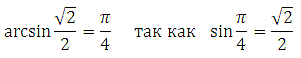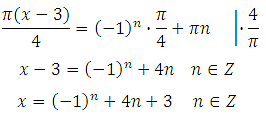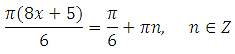Как найти наименьшее положительное решение уравнения

Математический детектив: поиск положительных целых решений уравнения

«Я экспериментировал с задачами кубического представления в стиле предыдущей работы Эндрю и Ричарда Гая. Численные результаты были потрясающими…» (комментарий на MathOverflow)

Вот так ушедший на покой математик Аллан Маклауд наткнулся на это уравнение несколько лет назад. И оно действительно очень интересно. Честно говоря, это одно из лучших диофантовых уравнений, которое я когда-либо видел, но видел я их не очень много.

Я нашёл его, когда оно начало распространяться как выцепляющая в сети нердов картинка-псевдомем, придуманная чьим-то безжалостным умом (Сридхар, это был ты?). Я не понял сразу, что это такое. Картинка выглядела так:

«95% людей не решат эту загадку. Сможете найти положительные целочисленные значения?»

Вы наверно уже видели похожие картинки-мемы. Это всегда чистейший мусор, кликбэйты: «95% выпускников МТИ не решат её!». «Она» — это какая-нибудь глупая или плохо сформулированная задачка, или же тривиальная разминка для мозга.

Но эта картинка совсем другая. Этот мем — умная или злобная шутка. Примерно у 99,999995% людей нет ни малейших шансов её решить, в том числе и у доброй части математиков из ведущих университетов, не занимающихся теорией чисел. Да, она решаема, но при этом по-настоящему сложна. (Кстати, её не придумал Сридхар, точнее, не он полностью. См. историю в этом комментарии).

Вы можете подумать, что если ничего другое не помогает, то можно просто заставить компьютер решать её. Очень просто написать компьютерную программу для поиска решений этого кажущегося простым уравнения. Разумеется, компьютер рано или поздно найдёт их, если они существуют. Большая ошибка. Здесь метод простого перебора компьютером будет бесполезен.

Не знаю, удастся ли уместить полное решение в статью, если не принять, что все уже знают всё необходимое об эллиптических кривых. Я могу привести здесь только краткий обзор. Основной справочный источник — это чудесная, относительно недавняя работа Бремнера и Маклауда под названием «An unusual cubic representation problem» («Необычная проблема кубического представления»), опубликованная в 2014 году в Annales Mathematicae et Informaticae.

Мы ищем положительные целочисленные решения уравнения

(я заменил обозначения переменных теми, которые используются в работе).

Первое, что нужно сделать, исследуя любое уравнение — попробовать поместить его в нужный контекст. Надо задать вопрос: что это за уравнение? Так, нас просят найти целочисленные решения, то есть это задача теории чисел. В текущей формулировке в уравнении используются рациональные функции (многочлены, делящиеся на другие многочлены), но очевидно, что мы можем домножить на общее кратное знаменателей, чтобы подчистить уравнение и получить только многочлены, то есть привести его к виду диофантова уравнения. Требование «положительности» довольно необычно, и, как мы увидим, усложняет всё.

Итак, сколько же у нас тут переменных? Вопрос кажется глупым: очевидно, что три, а именно , и . Но не торопитесь. Опытный исследователь теории чисел мгновенно заметит, что уравнение однородное. Это значит, что если является одним из решений уравнения, то решением является и . Понимаете, почему? Умножив каждую переменную на какую-нибудь постоянную ( — это просто пример), мы ничего не изменим, потому что константа в каждой из частей сокращается.

Это значит, что уравнение только притворяется трёхмерным. На самом деле оно двухмерно. В геометрическом представлении у нас есть поверхность (одно уравнение с тремя переменными в общем случае задаёт двухмерную поверхность. В целом, уравнений с переменными задают -мерное многообразие, где ). Но эта поверхность на самом деле ограничена линией, колеблющейся и проходящей через начало координат. Получившуюся поверхность можно понять, разобравшись в том, как она рассекает единичную плоскость. Это проективная кривая.

Проще всего объянить это сведение можно так: мы можем разделить решения, какими бы они ни были, на те, при которых , и те, при которых . В первом случае у нас остаётся всего две переменные, и , а во втором мы просто можем разделить на и получить решение при . Поэтому мы можем просто искать рациональные решения в и для случая , умножать их на общий делитель и получать целочисленное решение в , и . В сущности, целочисленные решения однородных уравнений соответствуют рациональным решениям неоднородной версии, которая на одну размерность меньше.

Продолжим: какова степень нашего уравнения? Степень уравнения — это максимальная степень, любого появляющаяся в уравнении одночлена, где «одночлен» — это произведение нескольких переменных, чья «степень» является количеством перемножаемых одночленов. Например, будет одночленом степени .

Поведение диофантовых уравнений сильно зависит от их степени. В целом:

Со степенью всё просто.
Степень полностью проанализирована и может быть решена довольно элементарными способами.
Степень — это обширный океан глубокой теории и миллион нерешённых проблем.
Степень и выше… Очень, очень сложны.

Мы имеем степень . Почему? Мы просто умножаем на делители:

Даже без раскрывания скобок можно увидеть, что степень равна : мы никогда не перемножаем более трёх переменных за раз. У нас получатся части типа , и , но никогда не будет чего-то больше трёх множителей. Если провести преобразования, то уравнение будет иметь вид

Вы можете возразить, что умножение на делители невозможно, если какие-то из них оказываются равны . Это верно — действительно, наше новое уравнение имеет несколько решений, не соответствующих исходному уравнению. Но на самом деле это хорошо. Версия с многочленами добавляет к оригиналу несколько «заплаток» и с ним становится проще работать. Нам просто нужно будет проверять, не исчезают ли исходные делители при каждом конкретном решении.

На самом деле уравнение с многочленами легко решить, например, , , . Это хорошо: у нас есть рациональное решение (рациональная точка). Это значит, что наше кубическое уравнение (степень = 3) на самом деле является эллиптической кривой.

Когда обнаруживаешь, что уравнение представляет собой эллиптическую кривую, то а) радуешься и б) отчаиваешься, потому что предстоит ещё много чего изучить. Это уравнение — прекрасный пример того, как мощную теорию эллиптических кривых можно применить к нахождению безумно сложно определяемых решений.

Первое, что обычно делают эллиптической кривой — приводят её в вейерштрассову форму. Это уравнение, которое выглядит как

(это называется развёрнутой вейерштрассовой формой. Она необязательна, но иногда более удобна).

Обычно любую эллиптическую кривую можно привести к такому виду (если вы только не работаете над полями с малыми характеристиками, но здесь нам не нужно о них волноваться). Объяснять способ поиска правильного преобразования было бы слишком долго, поэтому просто знайте, что это абсолютно механический процесс (критически важно в нём то, чтобы была хотя бы одна рациональная точка, которая у нас есть). Существуют разные пакеты вычислительной алгебры, которые сделают всё за вас.

Но даже если вы не знаете. как найти преобразование, проверить его очень просто, по крайней мере, это выполняется чисто механически. Необходимое преобразование в нашем случае задаётся страшно выглядящими формулами

Я знаю, что они похожи на неизвестно откуда взявшуюся магию вуду, но поверьте, это не так. Получив эти преобразования, с помощью монотонных, но довольно простых алгебраических расчётов мы покажем, что

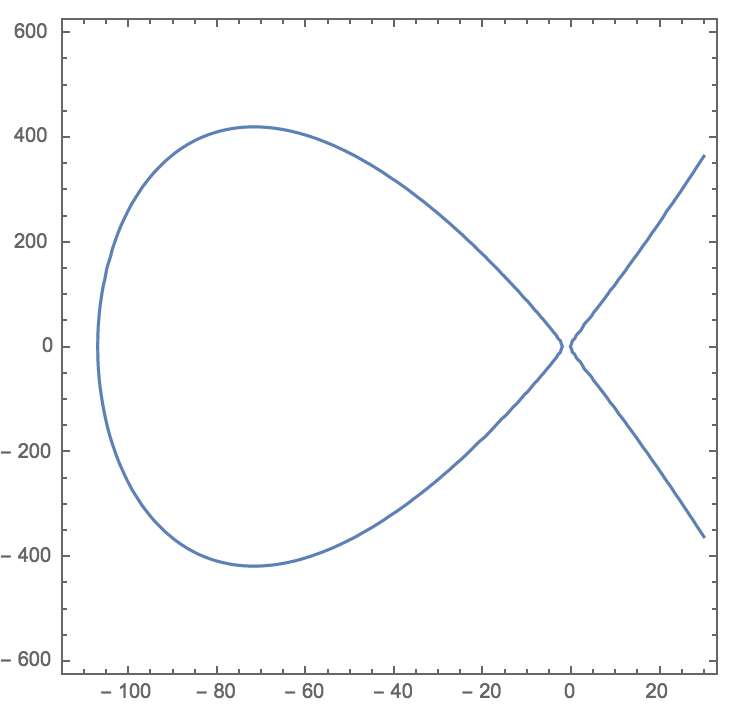
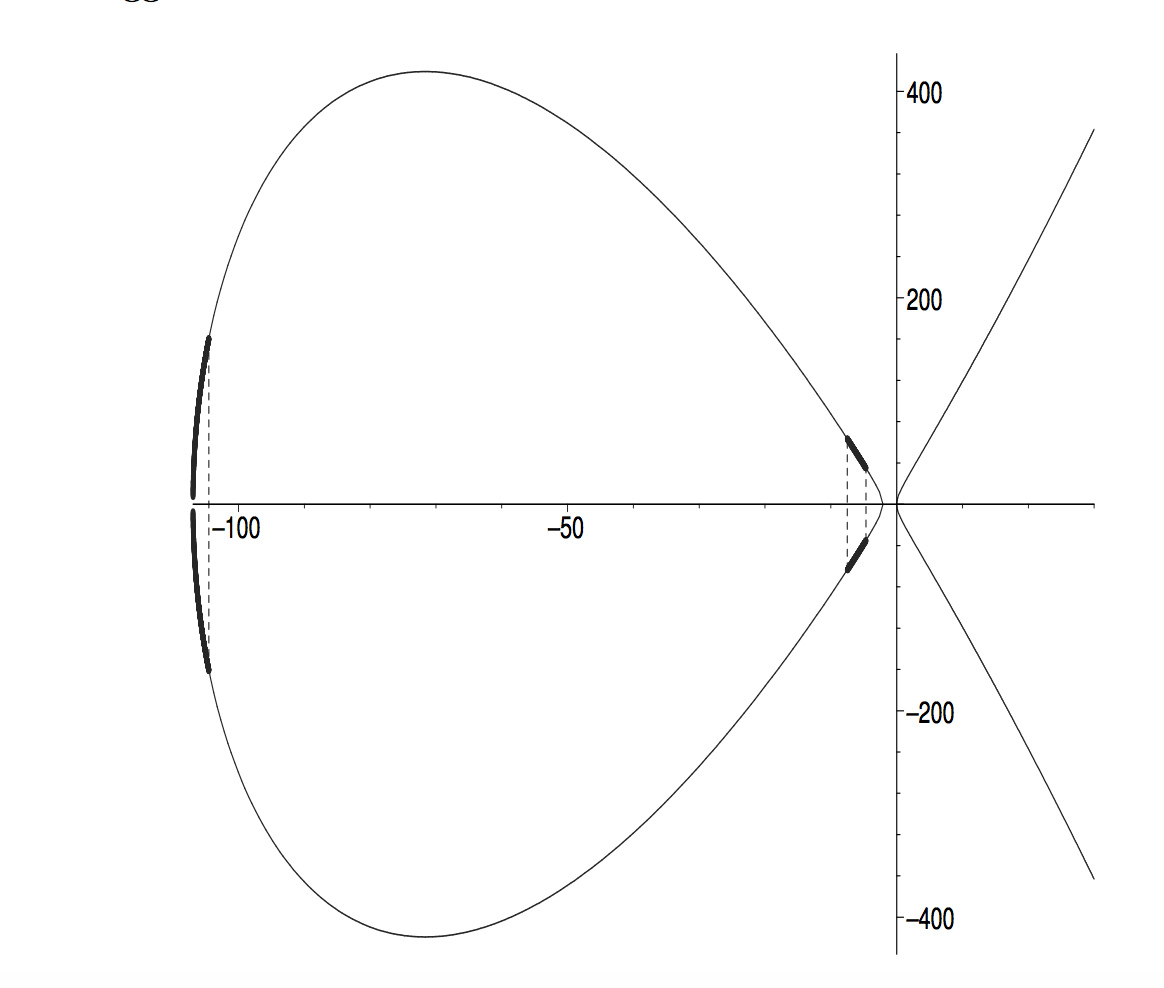
Это уравнение, хоть и выглядит совсем по-другому, на самом деле является достоверной моделью исходного. Графически оно выглядит так — типичная эллиптическая кривая с двумя вещественными частями:

«Рыбий хвост» справа растёт «в бесконечность и дальше». Овальная фигура слева является замкнутой и оказывается для нас довольно интересной.

Имея любое решение этого уравнения, мы можем восстановить необходимые значения , , с помощью уравнений

(Помните, что триплет нужно воспринимать проективно – какие бы значения вы ни получили с помощью этих уравнений, их всегда можно умножить на любую константу).

Два показанных нами отображения, из , , в , и наоборот, показывают, что эти два уравнения «одинаковы» с точки зрения теории чисел: рациональные решения одного дают рациональные решения другого. Технически это называется бирациональной эквивалентностью, а она является фундаментальным понятием алгебраической геометрии. Как мы уже заметили, могут существовать точки-исключения, которые не отображаются правильно. Это случаи, когда , или оказываются равны . Это привычная расплата в случае бирациональной эквивалентности, и она не должна вызывать никаких волнений.

Давайте рассмотрим пример.

На эллиптической кривой (2) есть хорошая рациональная точка:

, . Возможно, её не так просто найти, но очень просто проверить: просто вставьте эти значения и вы увидите, что две половины одинаковы (я выбирал эту точку не случайным образом, но пока это неважно). Можно просто проверить, какие значения , , она нам даёт. Мы получаем , , , и поскольку мы можем умножить на общий делитель, то результаты преобразуются в , , .

как можно с лёгкостью убедиться. Это простое решение нашего исходного уравнения в целых числах, но, увы, не в положительных целых. Это решение непросто вывести вручную, но и несложно получить без всей этой рассматриваемой здесь махины, приложив немного терпения. Самая сложность заключается в положительных решениях.

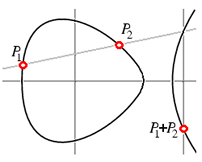
Теперь, получив рациональную точку на эллиптической кривой, например, на нашей кривой (2), можно начать генерировать другие с помощью техники хорд и касательных, рассмотренной в предыдущей статье на Quora.

Для начала прибавим нашу точку к ней самой, найдя касательную к кривой в точке и определив, где она снова встречается с кривой. Результат будет немного пугающим:

и снова эта новая точка соответствует значениям , , , являющимся решением исходного уравнения

Это решение определённо непросто найти вручную, но оно всё ещё под силу компьютеру. Однако оно по-прежнему неположительно.

Не пугаясь неудач, мы продолжаем вычислять , что можно определить соединением прямой линией и и нахождением третьей точки пересечения с кривой. И снова мы вычисляем , , , и снова результат неположителен. То же самое будет и с , и с , и так далее… пока мы не наткнёмся на .

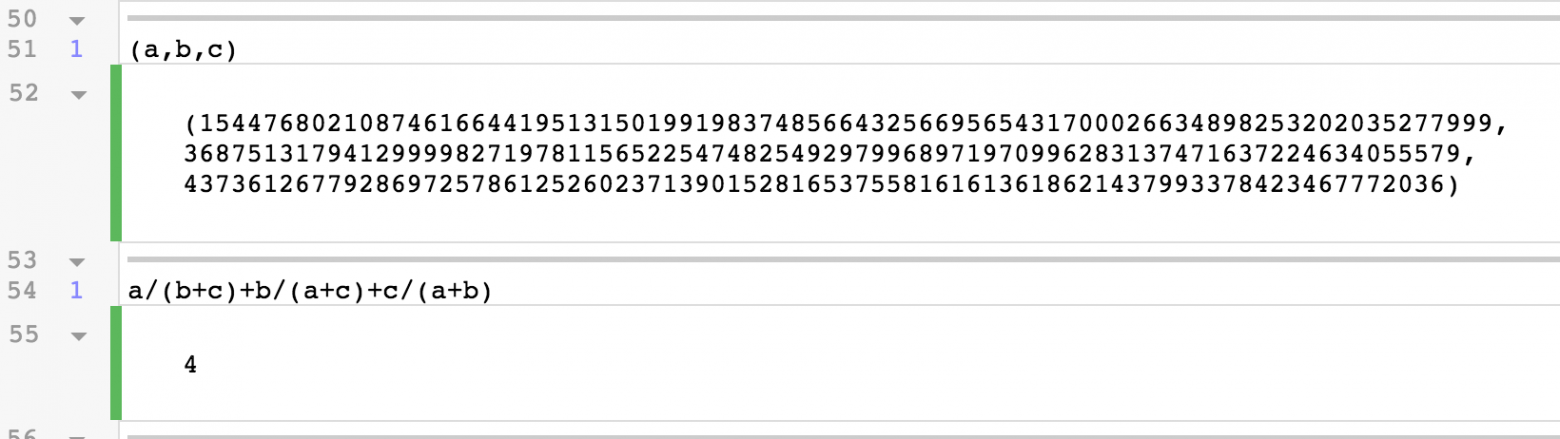
Его определённо непросто найти, но с помощью нашей машинерии нам достаточно повторить девять раз простую геометрическую процедуру. Соответствующие значения , , потрясающи:

a=154476802108746166441951315019919837485664325669565431700026634898253202035277999,
b=36875131794129999827197811565225474825492979968971970996283137471637224634055579,
c=4373612677928697257861252602371390152816537558161613618621437993378423467772036

Это 80-разрядные числа! Вы никак не смогли бы найти 80-разрядные числа на компьютере с помощью простого перебора. Выглядит невероятным, но вставив эти огромные числа в простое выражение , мы действительно получим ровно .

Фактически, они являются наименьшими решениями задачи. Если мы продолжим прибавлять к самой себе точку , то при этом просто будут расти делители. Непросто это доказать, потому что всегда есть вероятность сокращения, но теория высот для эллиптической кривой позволяет нам показать, что эти астрономические числа на самом деле являются простейшим решением уравнения.

Вернёмся к теории. Эллиптическая кривая над рациональными значениями имеет ранг, который является количеством точек, необходимых, чтобы использовать для метод хорд и касательных и быть уверенным, что мы рано или поздно найдём все рациональные точки на кривой. Наша эллиптическая кривая (2) имеет ранг 1. Это значит, что у неё есть бесконечное количество рациональных точек, но все они получаются из единственной, которая является ничем иным, как нашей точкой . Алгоритмы вычисления ранга и нахождения такого генератора далеки от тривиальных, но SageMath (теперь имеющий название CoCalc) выполняет их меньше чем за секунду всего в нескольких строках кода. Мой код можно посмотреть здесь. Он воспроизводит всё решение с нуля, но, конечно же, использует встроенные методы Sage для работы с эллиптическими кривыми.

В нашем случае точка лежит на овальной части кривой, как и точки для любого положительного целого . Они «кружатся» по овалу и постепенно довольно равномерно по нему распределяются. Это очень удачно, потому что только небольшая часть этого овала даёт положительные решения в отношении , , : это выделенная жирным часть графика ниже, взятого из работы Бремнера и Маклауда.

Точки , , и так далее, не лежат на выделенной части, а — лежит, именно так мы и получили наши 80-разрядные положительные решения.

Бремнер и Маклауд изучили, что происходит, если мы заменяем чем-то другим. Если вы думаете, что решения будут большими, то подождите, пока не увидите, какими окажутся решения при результате . Вместо 80 разрядов нам понадобится 398 605 460 разрядов. Да, это только количество разрядов решения. Если заменить результат на , то решение будет содержать триллионы разрядов. Триллионы. Для этого невинно выглядящего уравнения:

Поразительный пример того, как диофантовы уравнения с небольшими коэффициентами могут иметь огромные решения. Это внушает не просто трепет, а ощущение бездонности. Отрицательное решение десятой проблемы Гильберта означает, что рост решений при увеличении коэффициентов — это невычислимая функция, потому что если бы она была вычисляемой, то у нас был бы простой алгоритм решения диофантовых уравнений, а его не существует (ни простого, ни сложного). Соответствие 80-разрядные числа, числа из сотен миллионов разрядов и триллионы разрядов даёт нам небольшое представление о первых, небольших шагах этой чудовищной невычислимой функции. Немного измените числа в уравнении, и решения запросто превзойдут всё, что может вместиться в нашу жалкую, крошечную Вселенную.

Вот такое удивительно хитрое небольшое уравнение.

Благодарю пользователя MrShoor, приславшего мне ссылку на эту интересную статью.

Нам уже известны формулы для решения квадратных уравнений. А что делать, если встретится уравнение более высокой степени ? Оказы вается, что для уравнений третьей и четвёртой степени есть формулы, позволяющие найти корни (но они редко используются на практике ввиду их громоздкости), а для уравнений пятой степени и выше доказано, что таких формул не существует. Таким образом, у нас не выйдет в общем случае решить уравнение третьей или более высокой степени. Но существует ряд приёмов, позволяющих решить некоторые специальные виды уравнений. К их рассмотрению мы сейчас и перейдём.

Решите уравнение: `x^3 +4x^2 – 2x-3=0`.

Заметим, что `x=1` является корнем уравнения (значение многочлена при `x=1` равно сумме коэффициентов многочлена). Тогда по теореме Безу многочлен `x^3 +4x^2 -2x -3` делится на многочлен `x-1`. Выполнив деление, получаем:

`x^3 +4x^2 -2x -3=0 hArr (x-1)(x^2 + 5x +3) =0 hArr`

Обычно кубические уравнения решают именно так: подбирают один корень, выполняют деление уголком, после чего остаётся решить только квадратное уравнение. А что делать, если у нас уравнение четвёртой степени? Тогда придётся подбирать корень два раза. После подбора первого корня и деления останется кубическое уравнение, у которого надо будет подобрать ещё один корень. Возникает вопрос. Что делать, если такие «простые» числа как `+-1`, `+-2` не являются корнями уравне ния? Неужели тогда надо перебирать всевозможные числа? Ответ на этот вопрос даёт следующее утверждение.

Если несократимая дробь `p//q` (`p` – целое, `q` – натуральное) является корнем многочлена с целыми коэффициентами , то сво бодный член делится на `p` , а старший коэффициент делится на `q`.

Пусть несократимая дробь `p//q` – корень многочлена (8). Это означает, что

`a_n (p/q)^n +a_(n-1)(p/q)^(n-1) + a_(n-2) (p/q)^(n-2)+ . “+a_2 (p/q)^2 +a_1(p/q)+0=0`.

Умножим обе части на `q^n`, получаем:

`a_n p^n + a_(n-1) p^(n-1) q+a_(n-2) p^(n-2) q^2 + . + a_2 p^2 q^(n-2) +a_1 pq^(n-1)+a_0q^n=0`.

Перенесём в правую часть, а из оставшихся слагаемых вынесем `p` за скобки:

Справа и слева в (14) записаны целые числа. Левая часть делится на `p=>` правая часть также делится на `p`. Числа `p` и `q` взаимно просты (т. к. дробь `p//q` несократимая), откуда следует, что `a_0 vdotsp`.

Аналогично доказывается, что `a_n vdotsq`. Теорема доказана.

Как правило, предлагаемые вам уравнения имеют целые корни, поэтому в большинстве задач используется следующее: если у многочлена с целыми коэффициентами есть целые корни, то они являются делителями свободного члена.

а) `x^4+4x^3-102x^2-644x-539=0`; (15)

б) `6x^4-35x^3+28x^2+51x+10=0`. (16)

а) Попробуем найти целые корни уравнения. Пусть `p` – корень. Тогда `539vdotsp`; чтобы найти возможные значения `p`, разложим число `539` на простые множители:

Поэтому `p` может принимать значения:

Подстановкой убеждаемся, что `x=-1` является корнем уравнения. Разделим многочлен в левой части (15) уголком на `x+1` и получим:

Далее подбираем корни у получившегося многочлена третьей степени. Получаем `x=-7`, а после деления на `(x+7)` остаётся `(x+1)(x+7)(x^2-4x-77)=0`. Решая квадратное уравнение, находим окончательное разложение левой части на множители:

1) После того, как найден первый корень, лучше сначала выполнить деление уголком, и только потом приступать к поиску последующих корней. Тогда вычислений будет меньше.

2) В разложении многочлена на множители множитель `(x+7)` встретился дважды. Тогда говорят, что `(–7)` является корнем кратности два. Аналогично говорят о корнях кратности три, четыре и т. д.

б) Если уравнение имеет рациональный корень `x_0=p/q`, то `10vdotsp`, `6vdotsq`, т. е. `p in<+-1;+-2;+-5;+-10>`; `qin<1;2;3;6>`.Возможные варианты для `x_0`:

Начинаем перебирать числа из этого списка. Первым подходит число `x=5/2`. Делим многочлен в левой части (16) на `(2x-5)` и получаем

Заметим, что для получившегося кубического уравнения выбор рациональных корней заметно сузился, а именно, следующие числа могут быть корнями: `x_0=+-1,+-2,+-1/3,+-2/3`, причём мы уже знаем, что числа `+-1` и `+-2` корнями не являются (так как мы их подставляли раньше, и они не подошли). Находим, что `x=-2/3` – корень; делим `3x^3-10x^2-11x-2` на `3x+2` и получаем:

Решаем квадратное уравнение: `x^2-4x-1=0 iff x=2+-sqrt5`.

К сожалению, уравнения не всегда имеют рациональные корни. Тогда приходится прибегать к другим методам.

Разложите на множители:

а) `x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=`

Таким образом, сумму четвёртых степеней, в отличие от суммы квадратов, можно разложить на множители:

в) Вынесем `x^2` за скобки и сгруппируем:

Обозначим `x+2/x=t`. Тогда `x^2+4+4/x^2=t^2`, `x^2+4/x^2=t^2-4`, выражение в скобках принимает вид:

В итоге получаем:

Этот приём иногда используется для решения уравнений четвёртой степени; в частности, с его помощью решают возвратные уравнения (см. пример 12 е).

г)* Можно убедиться, что никакой из рассмотренных выше методов не помогает решить задачу, а именно: рациональных корней уравнение не имеет (числа `+-1` и `+-2` – не корни); вынесение числа `x^2` за скобки и группировка слагаемых приводит к выражению

Если здесь обозначить `4x-13/x=t`, то `x^2-2/x^2` через `t` рационально не выражается.

Прибегнем к методу неопределённых коэффициентов. Пусть

Попробуем подобрать коэффициенты `a`, `b`, `c`, `d` так, чтобы (17) обратилось в верное равенство. Для этого раскроем скобки в правой части и приведём подобные слагаемые:

Приравняем в (18) коэффициенты при одинаковых степенях в обеих частях уравнения. Получим систему уравнений:

Мы будем пытаться найти целочисленные решения системы (19). Найти все решения системы (19) не проще, чем решить исходную задачу, однако нахождение целочисленных решений – разумеется, если они есть – нам по силам.

Рассмотрим четвёртое уравнение. Возможны только два принципиально различных случая:

2) `b=2` и `d=-1`. Рассмотрим каждый из них. Подставляем значения `b` и `d` в первые три уравнения:

Из первого и третьего уравнений системы получаем `c=5/3`; `a=-17/3`, что не удовлетворяет второму уравнению, поэтому система решений не имеет; пара чисел `b=1` и `d=-2` не подходит.

Эта система имеет одно решение `a=-7`, `c=3`. Значит, числа `a=-7`, `b=2`, `c=3`, `d=-1` являются решением системы (19), поэтому

Далее каждый из квадратных трёхчленов можно разложить на множители.

Во многих ситуациях степень уравнения можно понизить с помощью замены переменных.

Неопределенные уравнения в математике с примерами решения и образцами выполнения

При изучении уравнений первой степени мы уже видели, что если число уравнений меньше числа неизвестных, то такая система имеет бесчисленное множество решений. Такие уравнения называются неопределёнными.

Наиболее часто в практике встречается случай одного уравнения с двумя неизвестными. Общий вид такого уравнения будет:
αx+by=c,
где x и у—неизвестные, а, b и с—данные коэффициенты.

Часто условия задачи бывают таковы, что правильный ответ на вопрос, поставленный в задаче, дают только целые значения, а иногда только целые и притом положительные значения.

Задача:

Разложить число 118 на такие два числа, из которых одно делилось бы на 11, а другое на 17.

Обозначая одно число через Их, а другое через 17у, мы получим уравнение:
11x+17y=118.

Так как в задаче ничего не сказано о знаке чисел, на которые нужно разложить число 118, то в данном случае мы можем считать ответом на задачу и отрицательные решения. Так, условию задачи удовлетворяют числа 33 и 85 (при х=3 и у=5), но также удовлетворяют и числа 220 и —102 (при х=20 и у=—6).

Задача:

Для упаковки самоваров имеются ящики, из которых в одни укладываются 4 самовара, в другие 7. Сколько нужно взять тех или других ящиков, чтобы упаковать 41 самовар?

Обозначив число малых ящиков через х, а число больших через у, будем иметь уравнение:
4x-+7y=41.

Очевидно, что по условию задачи здесь пригодны только целые и притом положительные решения. Такое решение данное уравнение допускает лишь одно, именно: x=5, у=3.

Таким образом, необходимо уметь решать неопределённые уравнения в целых числах, а также в целых и положительных числах.

Признак невозможности решения уравнения в целых числах

Если среди коэффициентов а, b и с имеются дробные, то мы можем привести все коэффициенты к одному знаменателю и затем его отбросить. Тогда все коэффициенты будут целыми числами.

Далее, если а, b и с имеют какой-либо общий множитель, то на него можно сократить обе части уравнения.

Итак, мы будем предполагать, что коэффициенты a, b и с —числа целые, не имеющие общего множителя.

Предположим теперь, что а и b имеют общим множителем некоторое целое число, отличное от 1. Пусть, например,
a=ma₁, b=mb₁.

Разделив все его члены на m, получим:

При целых значениях х и у левая часть уравнения представляет собой целое число, правая же часть — дробь, так как с, по предположению, не делится на m. Такое равенство невозможно. Следовательно:
Если коэффициенты при неизвестных неопределённого уравнения имеют общий множитель, которого не имеет свободный член, то уравнение не может иметь целых решений.

Поэтому во всех дальнейших рассуждениях мы будем предполагать числа а и b взаимно простыми.

Признак невозможности решения уравнения в положительных числах

Пусть в уравнении ax+by=c коэффициенты а и b положительны, а свободный член с — отрицателен. Тогда при всяких положительных значениях х и у левая часть уравнения будет положительной, а правая останется отрицательной. Такое равенство невозможно.

Если коэффициенты а и b отрицательны, а с — положительно, то, умножив все члены уравнения на —1, мы сведём этот случай к предыдущему. Итак:
Если коэффициенты при неизвестных неопределённого уравнения имеют знаки, противоположные знаку свободного члена, то уравнение не имеет положительных решений.

Общая формула корней неопределённого уравнения

Предположим, что каким-либо способом (например, путём непосредственных проб) мы нашли одно целочисленное решение неопределённого уравнения:
ax+by=с.

Пусть это решение будет х=а и y=β. Подставляя значение x и у в данное уравнение, получим тождество:
a a+bβ =c.

Вычитая почленно это тождество из данного уравнения, получим:
α(x-α)+b(y-β)=0,
откуда:
ax=aa — b(y—β), или

Для того чтобы x было целым числом, необходимо и достаточно, чтобы выражение было целым числом (так как а—число
целое). Другими словами, необходимо и достаточно, чтобы выражение b(y-β) нацело делилось на а. Но, по предположению, b — число взаимно простое с а, следовательно, необходимо (и достаточно), чтобы разность у—β нацело делилась на а. Обозначив целое частное от деления у— β на а через t (оно может быть и положительным и отрицательным), получим:
откуда y=β+at.

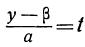
Подставляя в формулу для х число t вместо дроби 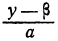, получим:
x = a-bt.

Таким образом, мы имеем для корней неопределённого уравнения формулы:
x = a-bt, y=β+at.

Давая в этих формулах t произвольные целые значения, положительные и отрицательные, мы получим бесчисленное множество целых решений данного неопределённого уравнения. В частности, при t=0 получим решение х = а; y=β, найденное нами уже ранее.

Присматриваясь к найденным формулам, легко заметить, что они составлены по следующему правилу:

Первым членом формулы является найденное частное значение данного неизвестного.
Вторым членом формул является произвольное целое число t, умноженное на коэффициент данного уравнения, причём в формуле для x берётся коэффициент при у в данном уравнении, а в формуле для у берётся коэффициент при х.
Один из коэффициентов берётся с обратным знаком.

Нетрудно видеть, что совершенно безразлично, который из коэффициентов мы берём с тем же знаком, с каким он стоит в уравнении и который берём с обратным знаком. В самом деле, формулы:
x=a-bt, y=β+at и x=a+bt, y=β -at
будут давать одни и те же решения; только те решения, которые одни формулы дают при положительных значениях t, другие будут давать при равных по абсолютной величине отрицательных значениях t.

Пример:

Непосредственной подстановкой убеждаемся, что уравнение удовлетворяется значениями х=2 и у=4. Тогда все остальные решения найдутся из формул:
x=2+5t, у=4—3t, или х=2—5t, y=4+3t.

Давая в этих формулах t произвольные целые значения, будем получать различные целочисленные решения данного уравнения. Например, взяв первые формулы, будем иметь:

t	0	1	2	3	-1	-2	…
x	2	7	12	17	-3	-8	…
y	4	1	-2	-5	7	10	…

Если бы мы взяли вторые формулы, то те же решения получили бы, давая t последовательно значения: 0; —1; —2; —3; 1; 2 и т. д.

Таким образом, задача решения в целых числах неопределенного уравнения сводится к нахождению какого-либо одного решения.

Способ подстановки

Для нахождения одного решения неопределённого уравнения можно пользоваться следующим способом. Пусть дано уравнение:
ах+by=с.

Определим из него одно из неизвестных в зависимости от другого (лучше взять то, у которого коэффициент меньше). Пусть, например, a Частный вид неопределённого уравнения

Неопределённое уравнение легко решается в общем виде, когда один из коэффициентов при неизвестных равен единице. Пусть, например, равен единице коэффициент при х. Будем иметь:
x+by=c.
Определим х:
x=c-by.

Очевидно, что любому целому значению у будет соответствовать целое же значение х.

Пример:

Дано уравнение: 5x+y=18.
Находим:
у = 18—5х.
Давая x произвольные целые значения, будем соответственно получать целые значения для у:

x 0 1 2 3 4 -1 -2 …

y 18 13 8 3 -2 23 28 …

Общее решение неопределённого уравнения

Покажем на примере способ решения неопределённого уравнения с любыми коэффициентами. Пусть дано уравнение:
23x+53y=109.

Определим из этого уравнения то неизвестное, у которого коэффициент меньше, в данном случае х:

или, исключив целую часть:

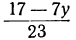
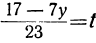
Для того чтобы x было целым при у целом, необходимо и достаточно, чтобы выражение было каким-нибудь целым числом. Обозначив последнее через t, будем иметь:
, или 17—7y=23t, 23t+7y=17

Если мы найдём для у и t такие целые значения, которые удовлетворяют уравнению 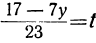, или, что то же, уравнению:
23t+7y=17,
то тем самым мы найдём соответствующие целые значения для х, и наша задача будет решена. Таким образом, решение данного уравнения мы свели к решению другого, более простого уравнения, у которого коэффициенты меньше, чем у данного.

По отношению к новому уравнению поступаем таким же образом. Определяем из него у:

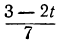
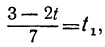
Для того чтобы у было целым, необходимо и достаточно, чтобы было целым числом. Обозначив это число через t₁, будем иметь:
, или 7t₁+2t=3.

При целых t и t₁, удовлетворяющих последнему уравнению, мы получим соответственно целые значения для х и у, удовлетворяющие данному уравнению. Следовательно, наша задача свелась к решению последнего уравнения, у которого коэффициенты ещё меньше. Поступаем с ним так же, как и прежде:

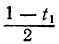
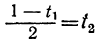
Приравняв выражение целому числу t₂, получим:
, или 2t₂+t₁=1.

Мы получили уравнение, в котором коэффициент при одном из неизвестных равен единице, а такие уравнения решать мы уже умеем. Решив его, получим:
t₁=1-2t₂.

Давая в этом уравнении произвольные целые значения t₂, будем получать целые значения для t₁. Подставляя найденные целые значения t₁ и t₂ в выражение для t: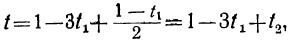

получим соответствующие целые значения для t. Подставляя соответствующие пары значений t и t₁ в выражение для у:

получим соответствующие целые значения для у. Наконец, делая подстановку найденных значений для у и t в выражение для х:

получим соответствующие целые значения для х.

Можно, однако, прямо выразить х и у в зависимости от t₂. Для этого подставим в выражение для t вместо t₁ его выражение через t₂:
t=1-3t₂+t₂=1-3 (1—2t₂)+t₂ ,
или
t=-2+7t₂ .

Подставим теперь в выражение для у вместо t и t₁ их выражения через t₂:
y=2-3t+t₁=2-3(-2+7t₂) + (1- 2t₂),
или
y=9-23t₂.

Наконец, подставляя найденные значения у и t в выражение для х, получим:
x=4-2y+t=4-2(9-23t₂)+(-2+7t₂),
или
x=- 16+53t₂ .

Таким образом, мы получим для х и у формулы:
x= — 16+53t₂, y=9-23t₂.

Давая в них произвольные целые значения для t₂, как положительные, так и отрицательные, будем получать бесчисленное множество решений данного уравнения; некоторые из них помещены в следующей таблице:

t₂ 0 1 2 -1 -2

x -16 37 90 -69 -122

y 9 -14 -37 32 55

Рассматривая операции, которые производились над коэффициентами данного и следующих уравнений, можно заметить такую последовательность:

Больший коэффициент данного уравнения 53 делили на меньший 23; получили частное 2 и остаток 7.

Меньший коэффициент данного уравнения 23 делили на остаток 7; получили частное 3 и второй остаток 2.

Первый остаток 7 делили на второй остаток 2; получили частное 3 и третий остаток 1.

Другими словами, мы поступали точно так, как если бы находили общий наибольший делитель коэффициентов данного уравнения.

Мы знаем, что два взаимно простых числа имеют общим наибольшим делителем единицу. А так как в неопределённом уравнении мы всегда предполагаем коэффициенты при неизвестных взаимно простыми, то производя над уравнением указанные выше операции, мы всегда придём к такому уравнению, у которого коэффициент при одном из неизвестных равен единице. Тем самым мы находим решения и данного уравнения. Отсюда следует:

Если коэффициенты при неизвестных неопределённого уравнения-числа взаимно простые, то уравнение всегда имеет целые решения.

Упрощение решения уравнения. Иногда при решении неопределённого уравнения можно внести некоторые упрощения, позволяющие быстрее прийти к решению.

1. В случае, когда один из коэффициентов при неизвестных и свободный член имеют общий множитель, то на него можно сократить обе части уравнения, если надлежащим образом ввести новое неизвестное.

Пример:

Коэффициент 6 и свободный член имеют общим множителем 3. Следовательно, и член 5у должен делиться на 3, а так как 5 не делится на 3, то у должен быть кратным трём. Полагая у=3t, где t— целое число, будем иметь:
6x-15t=21,
или, по сокращении на 3:
2x-5t =7.

Решаем последнее уравнение:

Подставляя найденное значение в выражения, полученные для х и у, будем иметь:
x=3+2(-1+2t₁)+t₁ =1+5t₁;
y=3(-1+2t₁) = -3+6t₁ .

Пример:

Дано уравнение: 9x+14y=105.
Полагая у=3t и сокращая обе части уравнения на 3, получим:
3x+14t=35.

Полагая в этом уравнении x=7t₁ и сокращая обе части уравнения на 7, получим:
3t₁ +2t=5.

Решаем последнее уравнение:

Произведя последовательные подстановки, получим:
t=2-(1-2t₂) + t₂ = 1+3t₂;
x=7t₁=7(1-2t₂)=7-14t₂ ;
y=3t=3(1+3t₂) = 3+9t₂ .

2. Если в приравниваемом целому числу выражении члены, находящиеся в числителе, имеют общий множитель, то решение уравнения можно упростить.

Пример:

Дано уравнение: 12x+17y=41.
Решаем его относительно х:

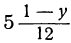
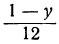
Для того чтобы выражение было целым числом, необходимо и достаточно, чтобы было целым числом.

Приравнивая это выражение целому числу t, получим: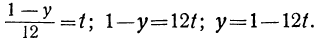

Соответственно получаем для х:
x=3-(1-12t)+5t=2+17t

3. Если при выделении целой части остаток будет более половины делителя, то удобно ввести отрицательный остаток.

Пример:

Дано уравнение: 11х—20y=49.
Решим его относительно х:

Произведя подстановки, получим:
y=2-5(1-2t₁)+t₁ = -3+11t₁;
x=4+2(-3+ 11t₁)+(1-2t₁) = -1+20t₁.

Если бы решали данное уравнение обычным способом, то получили бы для х:

и следующее уравнение было бы:

Это уравнение сложнее уравнения, полученного нами при помощи введения отрицательного остатка:
11t+2y=5.

Пример:

Дано уравнение: 15x+28y=59.
Решаем уравнение относительно х, вводя отрицательные остатки:

Попробовав решить приведённые в примерах уравнения обычным путём, легко убедимся, что без применения указанных упрощений все они потребовали бы для решения большего числа операций.

Положительные решения

Как уже говорилось ранее, часто из всех найденных решений неопределённого уравнения нужно взять лишь те, которые дают одновременно положительные значения для х и у. Найдя общие формулы для х и у, можно сразу определить, при каких значениях произвольного множителя будут получаться целые и положительные значения х и у.

Для того чтобы x и у были положительными, необходимо брать для t только такие значения, при которых:
a+bt>0; β-αt>0.

Будем считать а числом положительным. (Это мы всегда имеем право предположить, так как в противном случае мы могли бы обе части уравнения умножить на —1.) Тогда могут встретиться три различных случая.

1. Оба неравенства одинакового смысла. Это случится когда b — число отрицательное. В самом деле, пользуясь свойствами неравенства, будем иметь:
bt > — a ; at 0; 2+-5t>0,
или

Взяв для t любое целое число, большее 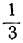(или, что то же, большее нуля), мы будем получать бесчисленное множество пар положительных значений х и у, удовлетворяющих данному уравнению.

Пример:

Решаем уравнение:

Ищем положительные решения:
1 —3t>0; 7 —8t>0,
или

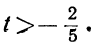
Любое целое значение t, меньшее 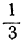(т. е. 0, —1, —2, …), даёт целые и положительные значения для х и у.

2. Неравенства противоположного смысла, причём они противоречат одно другому. Пусть, например, мы получим следующие неравенства:

Очевидно, что не существует таких значений t, которые одновременно удовлетворяли бы обоим неравенствам. В этом случае уравнение не может иметь положительных решений.

Пример:

4x+5y=-7.
Решая это уравнение, получим:
х=— 3+5t; y=1—4t.
Отсюда:
— 3+5t>0; 1 — 4t>0,
или

Неравенства противоречат друг другу; уравнение не имеет положительных решений.

3. Неравенства противоположного смысла, причём они не противоречат друг другу. Пусть, например, мы получили неравенства:

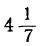
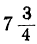
Все целые значения t, заключающиеся между и , т. е. 5,
6 и 7, дадут для х и у положительные решения. Таким образом, в этом случае:

Уравнение имеет столько целых положительных решений, сколько целых чисел заключено между найденными пределами для t.

Заметим, что, в частности, уравнение и здесь может не иметь положительных решений. Это будет тогда, когда между найденными пределами для t не содержится ни одного целого числа. Например, пусть мы получим неравенства:

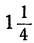
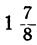
Неравенства не противоречат друг другу, но между и не
находится ни одного целого числа. Уравнение не имеет целых положительных решений.

Пример:

3x+7y=55.
Решаем уравнение: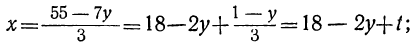

у=1 — 3t; x= 16+7t.

Отсюда:
1 —3t>0; 16+7t> 0,
или

Очевидно, для / можно взять лишь значения: 0; —1; —2. Получаем три решения уравнения:

t 0 -1 -2

x 16 9 2

y 1 4 7

Пример:

5. 5x+4y=3.
Решая уравнение, получим:
х=— 1 + 4t; у=2 —5t.
Отсюда:

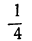
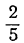
Неравенства не противоречат друг другу; но между и нет целых чисел. Уравнение не имеет целых положительных решений.

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

[spoiler title=”источники:”]

http://zftsh.online/articles/5013

http://lfirmal.com/neopredelennye-uravneniya/

[/spoiler]

Источник

ОТДЕЛЕНИЕ XI.

НЕОПРЕДЛЕННЫЙ АНАЛИЗ .
ИССЛЕДОВАНИЕ УРАВНЕНИЙ.

§ 5. Рeшениe неопредeленных уравнений первой степени.

Уравнение ах + bу = с данноe в отдeльности, имeeт бесчисленное множество пар корнeй. Значение одного нeизвeстного может быть выбрано совершенно произвольно, а соотвeтствующee значениe другого неизвeстного опредeляется данным уравнением на основании сдeланного выбора.

Сущность рeшения нeопредeленного уравневия состоит в отыскании цeлых значений для обоих неизвeстных. Для этого необходимо, чтобы в уравнeнии, окончательно сокращенном, коэффициенты а и b при нeизвeствых нe имeли никакого общего множителя. Напр., уравнениe 6x—9у=11 нe может быть рeшено в цeлых числах, т.е. х и у не могут быть одноврeмeнно цeлыми.

Когда условие возможности цeлых рeшений удовлетворяется, то число систем цeлых рeшeний неограничeнно.

Всe системы цeлых корней уравнения ах + bу = с заключeны в формулах х = т ± bt и , гдe т и п представляют одну какую-нибудь пару взаимно соотвeтствующих друг другу цeлых корней, а t есть произвольное цeлоe число. В формулу х-са входит коэффициeнт , соотвeтствующий в уравнении у-ку, а в
формулу у-ка входит коэффициeнт а,. соотвeтствующий х-су. Один из этих коэффициeнтов бeрется в формулах с перeмeной знака при нем; поэтому, когда в уравнении знаки у коэффициентов при нeизвeстных одинаковы, то в формулах члены, содeржащие t, бeрутся с разными знаками, и наоборот.

Вид прeдыдущих формул, разрeшающих данноe уравнeниe, показывает, что для составлeния этих формул нужно знать только т и п, т.-e. одну пару цeлых корнeй уравнeния, взаимно соотвeтствующих один другому. Поэтому, eсли удастся каким-нибудь способом найти подобную систему корней, то всe остальныя системы легко опредeляются. Требуемая система может быть нeрeдко пайдена догадкой, а вообще еe можно найти посредством последовательных подстановлeний, на
основании слeдующей теорeмы.

Если в уравнении ах + bу = с выразим одно из неизвeстных, напр., х, черeз другоe в видe и будeм подставлять вмeсто у ряд послeдоватeльных цeлых чисел, начиная с нуля и кончая числом а—1, то всегда, eсли только цeлые рeшения возможны, при одной из таких подстановок, числитель х-са раздeлится нацeло на его знамeнатeль.

В силу вышeуказанных замeчаний имeeтся слeдующий способ рeшения неопрeдeленного уравнения в цeлых числах, называемый способом подстановления:

Нужно выразить из уравненин то неизвeстноe, коэффициeнт которого мeньшe, затем подставлять в полученное дробноe выражениe вмeсто другого неизвeстного цeлые числа, начиная с нуля и в крайнем случаe до числа на eдиницу мeньшего знамeнатeля дроби, и, когда таким путем отыщется пара цeлых корней, то составить по этим корням и по обоим коэффициентам неизвeстных тe общие выражeния х – са и у – ка, которые заключают в себе всe системы
цeлых корнeй. Напр., имeя уравнениe 9х—7у =—6, находим , подставляем вмeсто х числа 0, 1, 2, 3 и наконeц при х = 4 находим у = 6; затeм, замeтив, что в данном уравнeнии коэффициенты нeизвeстных имeют разныe знаки, выписываeм общие формулы х = 4+ 7t и у = 6 + 9t с одинаковыми и притом, для удобства,
положитeльными знаками членов, содержащих t . Придавая количеству t произвольные, положительные или отрицательные значения, можем составить сколько угодно пар цeлых корней.

Вид общих формул х = т ± bt и показывает, что из них получаются по цeлому t цeлые х и у вслeдствие того, что неизвeстные входят в эти формулы с коэффициентами, равными единицe, отчего вычислениe х и у, не трeбуя дeлeний, и нe дает в результатах дробeй. Поэтому, если бы удалось посрeдством замeны
даннаго уравнения другими, совмeстными с ним, привести его к уравнению с коэффициентом единицей при одном из неизвeстных, то послeднеe уравнeниe разрeшалось бы в цeлых числах легко. Этого можно всегда достигнуть, умeньшая коэффициeнты послeдовательными дeлениями и вводя при этом вспомогатeльные нeизвeстные.

Такой способ рeшения, называемый способом послeдоватeльных дeлeний, объясняется подробно в курсах алгeбры. Успeх его основан на том, что при вычислениях по этому способу больший коэффициeнт дeлится на меньший, мeньший на первый остаток, пeрвый остаток на второй и т. д., а при таких дeлениях, когда притом коэффициeнты суть числа взаимно простые, мы всегда дойдeм до числа единицы. В курсах алгебры указываются также три случая, когда
процесс вычислeний может быть упрощен. Чтобы напомнить общий способ, возьмем примeр уравнeния 5х—13у=36. Выразив в нем неизвeстноe с меньшим коэффициентом и выдeлив из получeнной дроби цeлоe число, получим . Полагаем отчего получаем с одной стороны цeлую формулу х =7 + 2у + z, а с другой указанноe подстановкой вспомогательноe
уравнение между у и х. Преобразовав послeднeе таким же способом, получим Здeсь полагаем , отчего получается цeлая формула у= z + t и составляeтся ещe самой подстановкой второe вспомогатeльное уравнение мeжду z и t . Преобразовав новоe уравнeниe, находим . Здeсь полагаем , отчего получаeтся цeлая формула z = t + u и составляется уравнениe, приводящееся также к цeлой формулe t =2u—1. Всe найденные цeлые формулы мы выписываем в обратном порядкe, начиная с послeдней, и при этом всe неизвeстные послeдовательно выражаем чeрeз послeднеe неизвeстноe и. Таким образом доходим наконец до формул у
= 5и—2 и х =13и + 2, которые составлены по типу вышерассмотрeнных, разрeшающих формул и могут отличаться от подобных жe формул, найденных каким-нибудь другим способом рeшения, только частными значениями количеств т и п.

Если бы требовалось рeшить неопрeдeлeнноe уравнeние нe только в цeлых числах, но ещe нeпремeнно в положительных или отрицателных, или так, чтобы одно неизвeстное было положительно, а другоe отрицательно, то нужно найти сначала разрeшающие цeлые формулы, а затeм подчинить их подходящим неравенствам и рeшить полученные два неравенства, как совмeстные относитeльно входящего в них неопредeлeнного количества. Рeшeние неравенств даст предeлы для этого количества, при чем прeдeлы
могут оказаться, как извeстно из теории неравенств, или совпадающими, или ограничиваюшими, или в исключительном случаe противорeчащими. Принимая в соображение найденные предeлы неопредeлeнного количества, нужно нe забывать также, что это количeство должно быть во всяком случаe цeлым.

Обыкновенно неопредeленныя уравнения рeшаются только в положительных числах. При этом оказываeтся, что уравнениe вида ах + by = с, в котором всe коэффициенты положительны, имeет ограниченноe число рeшений, уравнeние ах— by = ±с, в котором знаки коэффициентов при нeизвeстных различны, имeет бесчислeнноe множество рeшений, и уравнениe ах + by = —с, в котором знак извeстного члeна
противоположен общeму знаку коэффициeнтов при нeизвeстных. совсeм нe имeет положительных рeшeний.

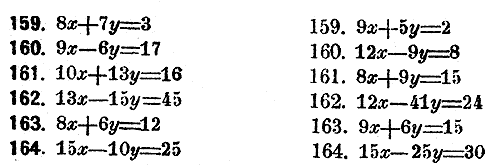
Решить слeдующие уравнения в цeлых числах способом подстановлeний:

Рeшить слeдующие уравнения в цeлых числах способом послeдовательных дeлений:

Могут ли быть рeшeны в цeлых и положительных числах слeдующие уравнения:

ответы

Следующие уравнения решить в целых и положительных числах.

Найти наименьшие положительные числа, удовлетворяющие следующим уравнениям:

Решить в целых положительных числах следующие системы уравнений:

ответы

191. Разложить число 200 на два слагаемых, из которых одно дeлилось бы без остатка на 7, а другое на 13.

191. Разложить число 116 на два слагаемых, из которых одно дeлилось бы без остатка на 8, а другое на 5

192. Сколькими и какими способами можно заплатить 149 руб, имeя билеты по 3 р. и по 5 р.?

192. Сколькими и какими способами можно заплатить 200 руб , имeя билеты по 3 р. и по 10 р.?

193. Найти два числа, разность которых 10, зная, что уменьшаемоe кратно 8-ми, а вычитаемоe кратно 17-ти.

193. Найти два числа, разность которых 12, зная, что уменьшаемоe кратно 7-ми, а вычитаемое кратно 15-ти

194. Сколькими и какими способами можно взвeсить груз в 114 фунтов, имeя гири в 5 и 3 фунта?

194. Сколькими и какими способами можно взвeсить груз в 87 фунтов, имeя гири в 5 и 2 фунта?

195. Двум артелям рабочих выдано 330 рублей. Каждый рабочий первой артели получил 16 руб., а каждый рабочий второй 9 руб.. Сколько было рабочих в каждой артели?

195. Двум артелям рабочих выдано 270 рублей. Каждый рабочий первой артели получил 13 руб., а каждый рабочий второй 8 руб.. Сколько было рабочих в каждой артели?

196. Найти двe дроби, сумма которых равна ¹⁹/₂₄, а знамeматели суть 12 и 24.

196. Найти две дроби, разность которых равна ⁸²/₁₄₃, а знаменатели суть 11 и 13.

197. Сколько можно поместить пятикопеечных и двухкопеечных монет на протяжении аршина, полагая, что диаметр первых равен ¹³/₁₆ вершка, а диаметр вторых ⁵/₈ вершка?

197. Сколько двугривенных и пятиалтынных можно поместить на протяжении фута, полагая, что диаметр первых равен ⁹/₁₀ дюйма, а диаметр вторых ⁵/₆ дюйма?

198. Дробь ⁷/₁₈ равна разности двух дробей, из которых у одной знаменатель 9, а у другой 12. Найти эти дроби.

198. Дробь 2³/₂₀ состоит из двух дробей, из которых у одной знаменатель 4, а у другой 5. Найти эти дроби. ‘

199. Из двух сортов серебра 56 и 84 пробы нужно образовать серебро 72 пробы. Как составить сплав в целых фунтах?

199. Из чистого серебра и серебра 80 пробы нужно образовать серебро 84 пробы. Как составить сплав в целых фунтах?

ответы

200. Из чистого спирта и спирта в 60 градусов нужно приготовить смесь в 75 градусов. Как составить смесь в целых ведрах?

200. Из спнрта в 90 и 55 градусов нужно приготовить смесь в 65 градусов. Как составить смесь в целых ведрах?

201. При каком значении х дробь 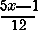обращается в положительное четное число?

201. При каком значении х дробь обращается в положительное нечетное число?

202. Найти общий вид чисел, кратных пяти, которые при делении на 8 дают в остатке 1.

202. Найти общий вид чисел, кратных семи, которые при делении на 5 дают в остатке 2.

203. При каком значении х дробь обращается в положительное число, делящееся на 4 с остатком 3?

203. При каком значении х дробь обращается в положительное число, делящееся на 7 с остатком 2?

204. Найти общий вид чисел, которые при делении на 3 дают в остатке 2, а при делении на 7 в остатке 3.

204. Найти общий вид чисел, которые при делении на 7 дают в остатке 4, а при делении на 8 в остатке 3.

205. А должен получить с В 25 рублей. Но у В есть только 40 трехрублевых билетов, а у А только 12 десятирублевых. Сколькими и какими способами они могут рассчитаться, обменивая билеты?

205. В должен получить с А 41 рубль. Но у А есть только 30 пятирублевых билетов, а у В только 25 трехрублевых. Сколькими и какими способами они могут рассчитаться, обменивая билеты?

206. Стрелок за каждый удачный выстрел получает по 8 коп., а за каждый неудачный сам платит по 27 к.. Сделав некоторое число выстрелов, меньшее 120, он выручил 97 коп.. Сколько было удачных выстрелов и сколько неудачных?

206. Стрелок за каждый удачный выстрел получает по 15 к., а за каждый неудачный сам платит по 34 коп.. Сделав некоторое число выстрелов, меньшее 150, он выручил 1 руб. 14 к. Сколько было удачных выстрелов и сколько неудачных?

207. В училище число учеников больше 100, но меньше 200. Если их рассадить на скамьи по 10 человек на каждую, то для одной скамьи недостанет полного числа, а сядут только 5 человек. Если же рассадить по 13 человек, то на одну скамью сядут 6 человек. Сколько учеников?

207. В училище число учеников больше 100, но меньше 200. Если их рассадить на скамьи по 12 человек на каждую, то для одной скамьи недостанет полного числа, а сядут только 9 человек. Если же рассадить по 10 человек, то на одну скамью сядут 7 человек. Сколько учеников?

208. Некто купил лошадей и волов на 1770 рублей, причем за каждую лошадь платил по 31 рублю, а за каждого вола по 22 р.. Известно притом, что число купленных лошадей кратно 10. Сколько куплено лошадей и волов?

208. Некто купил лошадей и волов на 2603 рубля, причем за каждую лошадь платил по 54 рубля, а за каждого вола по 23 р.. Известно притом, что число купленных лошадей кратно 7. Сколько куплено лошадей и волов?

209. Известно, что, откладывая по окружности шестую ее часть и десятую по противоположным направлениям, можно найти пятнадцатую ее часть. Какими способами может быть отделена эта искомая часть, если производить неоднократно последовательные отложения данных частей?

209. Известно, что, откладывая по окружности пятую ее часть и шестую по противоположным направлениям, можно найти тридцатую ее часть. Какими способами может быть отделена эта искомая часть, если производить неоднократно последовательные отложения данных частей?

ответы

210. При вращении двух зацепляющихся зубчатых колес, из которых одно имеет 19 зубцов, а другое 23, первый зубец одного колеса попал в первый промежуток другого. Сколко полных оборотов должны сделать оба колеса, чтобы первый зубец попал опять в первый промежуток, сколько, чтобы попал во второй промежуток, в третий и
т. д.?

210. При вращении двух зацепляющихся зубчатых колес, из которых одно имееть 25 зубцов, а другое 36, первый зубец одного колеса попал в первый промежуток другого. Сколько полных оборотов должны сделать оба колеса, чтобы первый зубец попал опять в первый промежуток, сколько, чтобы попал во второй промежуток, в третий и т. д.?

211. Разложить число 30 на три слагаемых так, чтобы сужма произведений первого слагаемого на 7, второго на 19 и третьего на 38 была равна 745.

211. Раздожить число 50 на 3 слагаемых так, чтобы сумиа произведений первого слагаемого на 8, второго на 13 и третьего на 42 была равна 1125.

212. Сколько иужно взять серебра 82-й, 66-й и 54 -й пробы, чтобы сделать слиток в 30 фунтов 72-й пробы?

212. Сколию нужно взять серебра 56-й, 72-й и 62 -й пробы, чтобы составить 27 фунтов 64-й пробы?

213. Найти трехзначное число, сумма цифр которого 20; если из этого числа вычесть 16 и остаток разделить на 2, то получится число, обозначенное прежними цифрами в обратномь порядке.

213. Найти трехзначное число, сумма цифр которого 16; если из этого числа вычесть 80 и разность умножить на 2, то получится число, обозначенное прежними цифрами в обратном порядке.

214. Продано 120 стоп бумаги трех сортов за 914 рублей. Стопа первого сорта продавалась за 13¹/₂ руб., второго за 9¹/₂ руб. и третьего за 3³/₄ руб.. Сколько продано бумаги каждого сорта?

214. Продано 100 стоп бумаги трех сортов за 465 рублей. Стопа первого сорта продавалась за 6 ³/₄руб., второго за 6 руб. ии третьего за 4¹/₂руб.. Сколько продано бумаги каждого сорта?

215. Найти трехзначное число, сумма цифр которого 16; если к этому числу прибавить 99, то получится число, обозначенное теми же цифрами в обратном порядке их.

215. Найти трехзначное число, сумма цифр которого 15;если из этого числа вычесть 297, то получится число, обозначенное теми же цифрами в обратном порядке их.

216. Найти наименьшее из чисел, которые при делении на 3, 4, 5 дают в остатках 1, 2 и 3.

216. Найти наименьшее из чисел, которые при делении на 3, 7 и 10 дают в остатках 2, 3 и 9.

217. Найти общий вид чисел, которые, будучи кратны 5- ти, при делении на 8, 11 и 3 дают остатки 1, 3 и 1.

217. Найти общий вид чисел, которые, будучи кратны 7-ми, при делении на 4, 5 и 9 дают остатки 3, 2 и 3.

218. Найти наименьшее из чисел, которые при делении ва 5, 6, 7 и 8 дают остатки 3, 1, 0 и 5.

218. Найти наименьшее из чисел, которые при делении на 3, 4, 5 и 7 дают остатки 1, 2, 3 и 4.

219. Заплатить 25 копеек монетами в 2, 3 и 5 копеек.

219. Заплатить 61 копейку монетами в 3, 5 и 10 копеек.

220. Разложить 2 в сумму трех дробей, знаменатели которых 3, 6 и 8.

220. Разложить 2 в сумму трех дробей, знаменатели которых 2, 5 и 10.

ОТВЕТЫ

Источник

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение $frac{6}{13}x^2=19frac{1}{2}$ . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь $frac{6}{13}$ умножается на x^2. А в правой части — смешанное число $19frac{1}{2}.$ Его целая часть равна 19, а дробная часть равна $frac{1}{2}.$ Запишем это число в виде неправильной дроби:

$19frac{1}{2}= frac{19cdot 2+1}{2} = frac{39}{2}.$

Получим:

$frac{6}{13}x^2=frac{39}{2};$

$x^2=frac{39cdot 13}{2cdot 6}=frac{13cdot 3cdot 13}{2cdot 6}=frac{{13}^2}{4};$

$x=pm frac{13}{2};$

или

Выбираем меньший корень.

Ответ: -6,5.

2. Решите уравнение

Возведем в квадрат левую часть уравнения. Получим:

Ответ: -6.

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как $frac{4x-5}{4x-5}$ и приведем дроби к общему знаменателю:

$frac{5x-3}{4x-5}-frac{4x-5}{4x-5}=0;$

$frac{x+2}{4x-5}=0;$

x= - 2.

Ответ: -2.

Это довольно простой тип уравнений. Главное – внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня – квадратного, кубического или n-ной степени.

4. Решите уравнение:

$sqrt{frac{6}{4{x}-54} } =frac{1}{7}.$

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

$frac{6}{4{x}-{ 54}} =frac{1}{49}.$

Решим пропорцию:

Условие при этом выполняется.

Ответ: 87.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

$left{begin{matrix} 72-x=x^2\72-xgeq 0 hfill \xgeq 0 hfill end{matrix}right.$ .

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

$sqrt{72-x}=x Leftrightarrow left{begin{matrix} 72-x=x^2\72-x geq 0 \x geq 0 end{matrix}right. Leftrightarrow$

Мы получили, что x=8 . Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: x=8 или x=-9. Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

Ответ: 8.

6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов:

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение $5^{x-7}=frac{1}{125}.$

Вспомним, что $125 = 5{}^{3}.$ Уравнение приобретает вид: $5{}^{x}{}^{-}{}^{7 }= 5{}^{-}{}^{3}.$ Функция y = 5^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

откуда x = 4.

Ответ: 4.

8. Решите уравнение ${left(frac{1}{49}right)}^{x-8}=7.$

Представим ${left(frac{1}{49}right)}^{ }$ как $7^{-2};$

${left(7^{-2}right)}^{x-8}=7;$

$7^{-2x+16}=7.$

Функция y = 7^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

x=7,5.

Ответ: 7,5.

9. Решите уравнение $left(frac{1}{9} right)^{{ x}-13} =3.$

Представим ${textstylefrac{1}{9}}$ в виде степени с основанием 3 и воспользуемся тем, что $left({ a}^{{ m}} right)^{{ n}} ={ a}^{{ mn}}.$

$left(3^{-2} right)^{{ x}-{ 13}} =3;$
$3^{-2{ x}+{ 26}} =3^{1} ;$

Ответ: 12,5.

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел.

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

${{log}_5 left(4+xright)=2 }.$

Область допустимых значений: . Значит,

Представим 2 в правой части уравнения как ${{log}_5 25 }$ , чтобы слева и справа в уравнении были логарифмы по основанию 5.

${{log}_5 left(4+xright)={{log}_5 25 } }.$

Функция $y = {{log}_5 x }$ монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом

4+x=25;
x=21.

Ответ: 21.

11. Решите уравнение: ${{log}_8 left(x^2+xright)={{log}_8 left(x^2-4right) } }.$

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: -4.

12. Решите уравнение: $2^{{{log}_4 left(4x+5right) }}=9.$

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

${{log}_4 b }=frac{{{log}_2 b }}{{{log}_2 4 }}=frac{{{log}_2 b }}{2}.$

Записываем решение как цепочку равносильных переходов.

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

${{log}_{x-5} 49=2 }.$

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Получим систему:

$small left{begin{matrix} left ( x-5 right )^2=49\x-50 \x-5 neq 1 end{matrix}right..$

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: x=12 и x=-2.

Очевидно, корень x=-2 является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения: x=12.

Ответ: 12.

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? – Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: $cos frac{pi (x+1)}{4}=frac{sqrt{2}}{2}.$ В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: $cos t=frac{sqrt{2}}{2}.$

Получаем решения: $t=pm frac{pi }{4}+2pi n, nin Z.$ Вернемся к переменной x.

$frac{pi (x+1)}{4}=pm frac{pi }{4}+2pi n, nin Z.$ Поделим обе части уравнения на и умножим на 4.

$left[ begin{array}{c}x=8n, nin Z \x=-2+8n end{array}right..$

Первой серии принадлежат решения

Вторая серия включает решения

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это x = -2.

Ответ: -2.

15. Решите уравнение: $tg frac{pi left( x+1right)}{4}= -1.$ В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: tgt=-1. Решения этого уравнения:

$t=-frac{pi }{4}+pi n, nin Z.$ Вернемся к переменной х:

$frac{pi left(x+1right)}{4}=-frac{pi }{4}+pi n, n in Z.$ Умножим обе части уравнения на 4 и разделим на .

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

Наименьший положительный корень x = 2.

Ответ: 2.

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Алгебра и начала математического анализа, 10 класс

Урок №9. Решение уравнений в целых числах.

Перечень вопросов, рассматриваемых в теме

понятие диофантовых уравнений;
теоремы для решения уравнений в целых числах;
основные методы решения уравнений в целых числах.

Глоссарий по теме

Диофантовыми уравнениями называются уравнения вида

P(x₁, x₂, …, x_n) = 0,

где P(x₁, …, x_n) – многочлен с целыми коэффициентами.

Неопределенные уравнения – уравнения, содержащие более одного неизвестного. Под одним решением неопределенного уравнения понимается совокупность значений неизвестных, которая обращает данное уравнение в верное равенство.

Теорема 1. Если НОД(а, b) = d, то существуют такие целые числа х и у, что имеет место равенство ах + bу = d.

Теорема 2. Если уравнение ах + bу = 1, если НОД(а, b) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и b.

Теорема 3. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с не делится на d, то уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с<d, то оно равносильно уравнению , в котором НОД = 1.

Теорема 5. Если в уравнении ах + bу = с НОД(а, b) = 1, то все целые решения этого уравнения заключены в формулах:

х = + bt, у = -at, где – целое решение уравнения ах + bу = 1,

t – любое целое число.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017. Шабунин М.И., Ткачева М.В., Федорова Н.Е.

Теоретический материал для самостоятельного изучения

Решение в целых числах алгебраических уравнений с целыми коэффициентами более чем с одним неизвестным представляет собой одну из труднейших и древнейших математических задач. Этими задачами много занимались самые выдающиеся математики древности, например, греческий математик Пифагор (VI век до н.э.), александрийский математик Диофант (III век н.э.), П.Ферма(XVII в.), Л.Эйлер(XVIII век), Ж.Л.Лагранж(XVIII век), П.Дирихле(XIX век), К.Гаусс(XIX век), П.Чебышев(XIX в.) и многие другие.

Решение уравнений в целых числах является важной задачей и для современной математики. Теоретический интерес уравнений в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.

Ещё в начальной школе на уроках математики перед нами часто ставили задачу выяснить, при каких допустимых значениях буквы обе части того или иного равенства принимают одинаковые числовые значения. На равенство в этом случае мы смотрели как на уравнение относительно указанной неизвестной величины. В восьмом классе мы познакомились с решением квадратных уравнений с одной переменной. Но, готовясь к олимпиадам, рассматривая контрольно- измерительные материалы Единого государственного экзамена встречаемся с заданиями, в которых предлагали уравнения с двумя переменными.

Диофантовыми уравнениями называются уравнения вида

P(x₁, x₂, …, x_n) = 0,

где P(x₁, …, x_n) – многочлен с целыми коэффициентами.

Применение теории делимости к решению неопределенных уравнений в целых числах.

Для решения в целых числах уравнения вида ах + by = c, где а, b, c – целые числа, отличные от нуля, приведем ряд теоретических положений, которые позволят установить правило решения. Эти положения основаны также на уже известных фактах теории делимости.

Теорема 1. Если НОД(а, b) = d, то существуют такие целые числа х и у, что имеет место равенство ах + bу = d.

(Это равенство называется линейной комбинацией или линейным представлением наибольшего общего делителя двух чисел через сами эти числа.)

Доказательство теоремы основано на использовании равенства алгоритма Евклида для нахождения наибольшего общего делителя двух чисел (наибольший общий делитель выражается через неполные частные и остатки, начиная с последнего равенства в алгоритме Евклида).

Пример.

Найти линейное представление наибольшего общего делителя чисел 1232 и 1672.

Решение.

1. Составим равенства алгоритма Евклида:

1672 = 1232 ∙1 + 440,

1232 = 440 ∙ 2 + 352,

440 = 352 ∙ 1 + 88,

352 = 88 ∙ 4, т.е. (1672,352) = 88.

2) Выразим 88 последовательно через неполные частные и остатки, используя полученные выше равенства, начиная с конца:

88 = 440 – 352∙1 = (1672 – 1232) – (1232 – 1672∙2 + 1232∙2) = 1672∙3 – 1232∙4, т.е. 88 = 1672∙3 + 1232∙(-4).

Справедливость этой теоремы следует из теоремы 1. Таким образом, чтобы найти одно целое решение уравнения ах + bу = 1, если НОД (а, в) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и в.

Пример.

Найти целое решение уравнения 15х + 37у = 1.

Решение.

1. 37 = 15 ∙ 2 + 7,

15 = 7 ∙ 2 + 1.

2. 1 = 15 – 7∙2 = 15 – (37 – 15∙2) ∙2 = 15∙5 + 37∙(-2),

т.е. – решение данного уравнения.

Теорема 3. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с не делится на d, то уравнение целых решений не имеет.

Для доказательства теоремы достаточно предположить противное.

Пример.

Найти целое решение уравнения 16х – 34у = 7.

Решение.

(16,34)=2; 7 не делится на 2, уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с<d, то оно равносильно уравнению , в котором НОД = 1.

При доказательстве теоремы следует показать, что произвольное целое решение первого уравнения является также решением второго уравнения и обратно.

Теорема 5. Если в уравнении ах + bу = с НОД(а, b) = 1, то все целые решения этого уравнения заключены в формулах:

х = х₀с + bt, у = y₀c-at, где х₀, y₀ – целое решение уравнения ах + bу = 1,

t – любое целое число.

При доказательстве теоремы следует показать, во-первых, что приведенные формулы действительно дают решения данного уравнения и, во-вторых, что произвольное целое решение этого уравнения заключено в приведенных формулах.

Приведенные теоремы позволяют установить следующее правило решения в целых числах уравнения ах+ bу = с НОД(а, b) = 1:

Находится целое решение уравнения ах + bу = 1 путем представления 1 как линейной комбинации чисел а и b (существуют и другие способы отыскания целых решений этого уравнения, например при использовании цепных дробей);
Составляется общая формула целых решений данного уравнения х = х₀с + bt, у = y₀c – at, где х₀, y₀ – целое решение уравнения ах + bу = 1, t – любое целое число.

Придавая t определенные целые значения, можно получить частные решения данного уравнения: наименьшие по абсолютной величине, наименьшие положительные (если можно) и т.д.

Пример.

Найти целые решения уравнения 407х – 2816у = 33.

Решение.

1. Упрощаем данное уравнение, приводя его к виду 37х – 256у = 3.

2.Решаем уравнение 37х – 256у = 1.

256 = 37∙ 6 + 34,

37 = 34 ∙1 + 3,

34 = 3 ∙11 + 1.

1 = 34 – 3∙11 = 256 – 37∙6 – 11 (37 – 256 + 37∙6) = 256∙12 – 37∙83 =

= 37∙(-83) – 256∙(-12),

т.е. х₀= -83, y₀= -12.

3. Общий вид всех целых решений данного уравнения:

х = -83∙3 – 256t = -249 – 256t,

у = -12∙3 – 37 t = -36 – 37 t.

Положив t = -1, получим х₁= 7, у₁= 1 и общие формулы решений примут вид: х = 7 – 256t, у = 1-37t.

2. Метод полного перебора всех возможных значений переменных,

входящих в уравнение.

Найти множество всех пар натуральных чисел, которые являются решениями уравнения 49х + 51у = 602.

Решение:

Выразим из уравнения переменную х через у , так как х и у – натуральные числа, то

602 – 51у ≥ 49,

51у≤553,

Полный перебор вариантов показывает, что натуральными решениями уравнения являются х=5, у=7.

Ответ: (5;7).

3. Решение уравнений методом разложения на множители.

Диофант наряду с линейными уравнениями рассматривал квадратные и кубические неопределенные уравнения. Решение их, как правило, сложно.

Рассмотрим такой случай, когда в уравнениях можно применить формулу разности квадратов или другой способ разложения на множители.

Решить уравнение в целых числах: х²+ 23 = у²

Решение:

Перепишем уравнение в виде: у²– х²= 23, (у – х)(у + х) = 23

Так как х и у – целые числа и 23 – простое число, то возможны случаи:

; ; ; ;

Решая полученные системы, находим:

; ;;;

Ответ: (-11;12);(11;12);(11;-12);(-11;-12).

4. Выражение одной переменной через другую и выделение целой части дроби.

Решить уравнение в целых числах: х²+ ху – у – 2 = 0.

Решение:

Выразим из данного уравнения у через х:

у(х – 1) =2 – х²,

Так как х, у – целые числа, то дробь должна быть целым числом.

Это возможно, если х – 1 =

; ;

Ответ: (0; -2); (2; -2).

5. Методы, основанные на выделении полного квадрата.

Найдите все целочисленные решения уравнения: х²– 6ху + 13у²= 29.

Решение:

Преобразуем левую часть уравнения, выделив полные квадраты,

х²– 6ху + 13у²= (х²– 6ху + 9у²) + 4у²= (х – 3у)²+ (2у)²= 29, значит (2у)² 29.

Получаем, что у может быть равен .

1. у = 0, (х – 0)²= 29. Не имеет решений в целых числах.

2. у = -1, (х + 3)²+ 4 =29, (х + 3)²= 25, х + 3 = 5 или х + 3 = -5

х=2 х=-8

3. у = 1, (х – 3)²+4 =29,

(х – 3)²=25, х – 3 = 5 или х – 3 = -5

х = 8 х = -2

4. у = -2, (х + 6)²+ 16 = 29, (х + 6)²= 13. Нет решений в целых числах.

5. у=2, (х-6)²+16=29, (х-6)²=13. Нет решений в целых числах.

Ответ: (2; -1); (-8; -1); (8; 1); (-2; 1).

6. Решение уравнений с двумя переменными как квадратных

относительно одной из переменных.

Решить уравнение в целых числах: 5х²+5у²+8ху+2у-2х+2=0.

Решение:

Рассмотрим уравнение как квадратное относительно х:

5х²+ (8у – 2)х + 5у²+ 2у + 2 = 0

D = (8у – 2)²– 4·5(5у²+ 2у + 2) = 64у²– 32у + 4 = -100у²– 40у – 40= = -36(у²+ 2у + 1) = -36(у + 1)²

Для того, чтобы уравнение имело решения, необходимо, чтобы D = 0.

-36(у + 1)²= 0. Это возможно при у = -1, тогда х = 1.

Ответ: (1; -1).

7. Оценка выражений, входящих в уравнение.

Решить в целых числах уравнение:

(х²+ 4)(у²+ 1) = 8ху

Решение:

Заметим, что если – решение уравнения, то – тоже решение.

И так как х = 0 и у = 0 не являются решением уравнения, то, разделив обе части уравнения на ху, получим:

Пусть х > 0, у > 0, тогда, согласно неравенству Коши,

тогда их произведение , значит,

Отсюда находим х = 2 и у = 1 – решение, тогда х = -2 и у = -1 – тоже решение.

Ответ: (2; 1); (-2; -1)

8.Примеры уравнений второй степени с тремя неизвестными.

Рассмотрим уравнение второй степени с тремя неизвестными: х²+ у²= z².

Геометрически решение этого уравнения в целых числах можно истолковать как нахождение всех пифагоровых треугольников, т.е. прямоугольник треугольников, у которых и катеты х,у и гипотенуза z выражаются целыми числами.

По формуле х = uv, , где u и v – нечетные взаимно простые числа (u > v > 0) можно найти те решения уравнения х²+ у²= z², в которых числа х,у и z не имеют общих делителей (т.е. взаимно простые).

Для начальных значений u и v формулы приводят к следующим часто встречающимся равенствам:

3²+ 4²= 5²(u = 1, v = 3), 5²+ 12²= 13²(u = 1, v = 5), 15²+ 8²= 17²(u = 3, v = 5)

Все остальные целые положительные решения этого уравнения получаются умножением решений, содержащихся в формулах, на произвольный общий множитель а.

Разбор решения заданий тренировочного модуля

№1. Тип задания: выбор элемента из выпадающего списка

Решите уравнение 9х+22у-1=0

Выпадающий список:

(-5; 2)
(5; 2)
(-5; -2)
(5; -2)

Решение: Решим данное уравнение, воспользовавшись теоремой 2:

1. 22 = 9 ∙ 2 + 4,

9 = 4 ∙ 2 + 1.

2. 1 = 9 – 4∙2 = 9 – (22 – 9∙2) ∙2 = 9∙5 + 22∙(-2),

т.е. х₀= 5, у₀= -2 – решение данного уравнения

Ответ: 4. (5; -2)

№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Найдите целое решение уравнения 3х+9у=3

х=____

у=____

Решение: Решим данное уравнение: 3х+9у=3

Разделим обе части уравнения на 3, получим:

х+3у=1

3 = 1 ∙ 2 + 1
1 = 3 – 1∙2, т.е. х₀= 1, у₀= 0 – решение данного уравнения

Ответ: х= 1, у= 0.

Источник

Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно. Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.

В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.

Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.

Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.

Понимание раздела «Тригонометрия» в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.

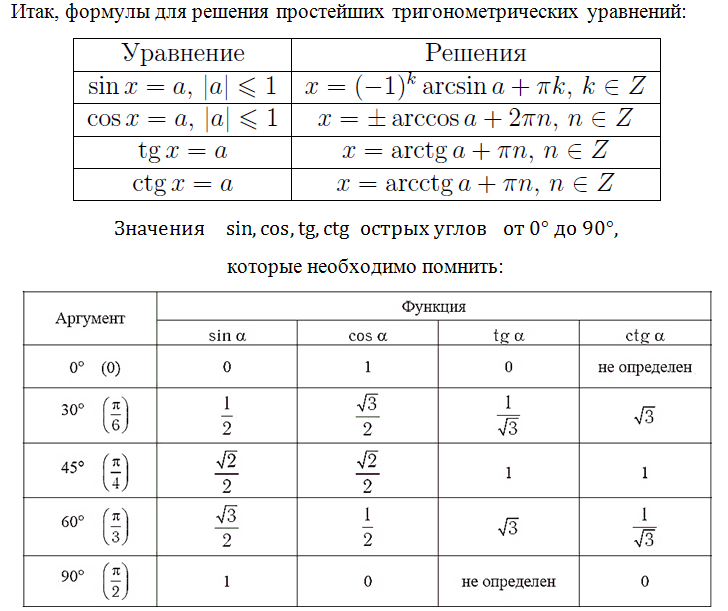
В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:

Знание этих значений необходимо, это «азбука», без которой невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да просто вы именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.

Алгоритм восстановления этих значений прост, он также приведён в теории, полученной вами во втором письме после подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».

Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с использованием угла х для соответствующих уравнений: cosx=a, sinx=a, tgx=a, где х может быть и выражением. В примерах ниже у нас аргумент задан именно выражением.

Итак, рассмотрим следующие задачи:

Найдите корень уравнения:

В ответе запишите наибольший отрицательный корень.

Решением уравнения cos x = a являются два корня:

Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.

Значит

Выразим x:

Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.

Общая рекомендация для всех подобных задач: для начала берите диапазон n от – 2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: – 3 и 3, – 4 и 4 и так далее.

Вычисляем:

При n = – 2 х₁= 3 (– 2) – 4,5 = – 10,5 х₂= 3 (– 2) – 5,5 = – 11,5

При n = – 1 х₁= 3 (– 1) – 4,5 = – 7,5 х₂= 3 (– 1) – 5,5 = – 8,5

При n = 0 х₁= 3∙0 – 4,5 = – 4,5 х₂= 3∙0 – 5,5 = – 5,5

При n = 1 х₁= 3∙1 – 4,5 = – 1,5 х₂= 3∙1 – 5,5 = – 2,5

При n = 2 х₁= 3∙2 – 4,5 = 1,5 х₂= 3∙2 – 5,5 = 0,5

Получили, что наибольший отрицательный корень равен –1,5

Ответ: –1,5

Решите самостоятельно:

Посмотреть решение

Решите уравнение:

В ответе напишите наименьший положительный корень.

Решением уравнения sin x = a являются два корня:

Либо (он объединяет оба указанные выше):

Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от – 90^о до 90^осинус которого равен a.

Значит

Выразим x (умножим обе части уравнения на 4 и разделим на Пи):

Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n = 0,1,2 …

При n = 0 х = (– 1)⁰ + 4∙0 + 3 = 4

При n = 1 х = (– 1)¹ + 4∙1 + 3 = 6

При n = 2 х = (– 1)² + 4∙2 + 3 = 12

Проверим при n = –1 х = (–1)^–1 + 4∙(–1) + 3 = –2

Значит наименьший положительный корень равен 4.

Ответ: 4

Решите самостоятельно:

Посмотреть решение

Решите уравнение:

В ответе напишите наименьший положительный корень.

Решением уравнения tg x = a является корень:

Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90^о до 90^о, тангенс которого равен a.

Значит

Выразим x (умножим обе части уравнения на 6 и разделим на Пи):

Найдём наименьший положительный корень. Подставим значения n = 1,2,3… Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:

Таким образом, наименьший положительный корень равен 0,25.

Ответ: 0,25

Решите самостоятельно:

Посмотреть решение

Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.

Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если в ходе решения вы не сможете определить угол, например, для

то данные формулы вам помогут:

Спасибо за внимание, учитесь с удовольствием!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Математический детектив: поиск положительных целых решений уравнения