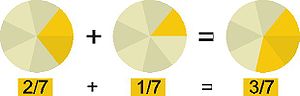
Как найти наименьшее рациональное число

Как найти наименьшее рациональное число

Рационáльное числó (от лат. ratio «отношение, деление, дробь») — число, которое можно представить в виде обыкновенной дроби {frac {m}{n}}, где m — целое число, а n — натуральное[1]. Пример: {frac {2}{3}}, где {displaystyle m=2}, а n=3.

Целые числа также могут быть записаны в виде дроби, например:

{displaystyle 1=1,0={frac {1}{1}};-4=-4,000={frac {-20}{5}}.}

Поэтому целые числа также являются рациональными. Таким образом, множество рациональных чисел представляет собой расширение множества целых чисел путём добавления к ним дробей.

Понятие дроби возникло несколько тысяч лет назад, когда, сталкиваясь с необходимостью измерять некоторые величины (длину, вес, площадь и т. п.), люди поняли, что целых чисел недостаточно и необходимо ввести понятие доли: половины, трети, четверти и т. п. Дробями и операциями над ними пользовались, например, шумеры, древние египтяне и греки.

Множество рациональных чисел[править | править код]

Множество рациональных чисел обозначается mathbb {Q} (от лат. quotient, «частное») и может быть записано в таком виде:

{displaystyle mathbb {Q} =left{{frac {m}{n}}mid min mathbb {Z} , nin mathbb {N} right}.}

При этом оказывается, что разные записи могут представлять одну и ту же дробь, например, {frac {3}{4}} и {frac {9}{12}}, (все дроби, которые можно получить друг из друга умножением или делением числителя и знаменателя на одно и то же натуральное число, представляют одно и то же рациональное число). Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:

{displaystyle mathbb {Q} =left{{frac {m}{n}}mid min mathbb {Z} , nin mathbb {N} , gcd(m,n)=1right}.}

Здесь gcd(m,n) — наибольший общий делитель чисел m и n.

Множество рациональных чисел является естественным обобщением множества целых чисел. Легко видеть, что если у рационального числа a={frac {m}{n}} знаменатель n=1, то a=m является целым числом.

Множество рациональных чисел располагается всюду плотно на числовой оси: между любыми двумя различными рациональными числами расположено хотя бы одно рациональное число (а значит, и бесконечное множество рациональных чисел). Тем не менее, оказывается, что множество рациональных чисел имеет счётную мощность (то есть все его элементы можно перенумеровать). Со времён древних греков известно о существовании чисел, не представимых в виде дроби: они доказали в частности, что {sqrt {2}} не рациональное число. Недостаточность рациональных чисел для выражения всех величин привела в дальнейшем к понятию вещественного числа. В отличие от множества вещественных чисел (которое соответствует одномерному пространству), множество рациональных чисел имеет меру нуль.

Терминология[править | править код]

Формальное определение[править | править код]

Формально рациональные числа определяются как множество классов эквивалентности пар {displaystyle left{(m,;n)mid m,nin mathbb {Z} ,nneq 0right}} по отношению эквивалентности (m,;n)sim (m',;n'), если mcdot n'=m'cdot n. При этом операции сложения и умножения определяются следующим образом:

  • left(m_{1},;n_{1}right)+left(m_{2},;n_{2}right)=left(m_{1}cdot n_{2}+m_{2}cdot n_{1},;n_{1}cdot n_{2}right);
  • left(m_{1},;n_{1}right)cdot left(m_{2},;n_{2}right)=left(m_{1}cdot m_{2},;n_{1}cdot n_{2}right).

Из определения видно, что никакие операции сложения или умножения не приводят к появлению пары вида {displaystyle (m,0).}

Связанные определения[править | править код]

Правильные, неправильные и смешанные дроби[править | править код]

Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Правильные дроби представляют рациональные числа, по модулю меньшие единицы. Дробь, не являющаяся правильной, называется неправильной и представляет рациональное число, большее или равное единице по модулю.

Неправильную дробь можно представить в виде суммы целого числа и правильной дроби, называемой смешанным числом. Например, 2{frac {3}{7}}=2+{frac {3}{7}}={frac {14}{7}}+{frac {3}{7}}={frac {17}{7}}. Подобная запись (с пропущенным знаком сложения), хотя и употребляется в элементарной арифметике, избегается в строгой математической литературе из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь.

Высота дроби[править | править код]

Высота обыкновенной дроби — это сумма модуля числителя и знаменателя этой дроби.
Высота рационального числа — это сумма модуля числителя и знаменателя несократимой обыкновенной дроби, соответствующей этому числу[2].

Например, чтобы узнать высоту дроби -{frac {15}{6}}, нужно сначала из неё получить несократимую дробь. Несократимая дробь будет выглядеть так: -{frac {5}{2}}. Потом нужно сложить модуль числителя и знаменатель: 5+2=7. Значит высота дроби -{frac {15}{6}} равна 7.

Комментарий[править | править код]

Термин дробное число (дробь) иногда[уточнить] используется как синоним к термину рациональное число, а иногда синоним любого нецелого числа. В последнем случае дробные и рациональные числа являются разными вещами, так как тогда нецелые рациональные числа — всего лишь частный случай дробных.

Свойства[править | править код]

Основные свойства[править | править код]

Множество рациональных чисел удовлетворяют шестнадцати основным свойствам, которые легко могут быть получены из свойств целых чисел.[3]

  1. Упорядоченность. Для любых рациональных чисел a и b ({displaystyle forall a,bin mathbb {Q} }) существует правило, позволяющее однозначно идентифицировать между ними одно и только одно из трёх отношений: «<», «>» или «=». Это правило называется правилом упорядочения и формулируется следующим образом:

  2. Операция сложения. Для любых рациональных чисел a и b ({displaystyle forall a,bin mathbb {Q} }) существует бинарная операция сложения, которая ставит им в соответствие некоторое рациональное число c. При этом само число c называется суммой чисел a и b и обозначается left(a+bright), а процесс отыскания такого числа называется сложением. Правило сложения имеет следующий вид: {displaystyle a={frac {m_{a}}{n_{a}}},;b={frac {m_{b}}{n_{b}}}:a+bequiv {frac {m_{a}}{n_{a}}}+{frac {m_{b}}{n_{b}}}={frac {m_{a}cdot n_{b}+m_{b}cdot n_{a}}{n_{a}cdot n_{b}}}}
  3. Операция умножения. Для любых рациональных чисел a и b ({displaystyle forall a,bin mathbb {Q} }) существует бинарная операция умножения, которая ставит им в соответствие некоторое рациональное число c. При этом само число c называется произведением чисел a и b и обозначается left(acdot bright), а процесс отыскания такого числа также называется умножением. Правило умножения имеет следующий вид: {displaystyle a={frac {m_{a}}{n_{a}}},;b={frac {m_{b}}{n_{b}}}:acdot bequiv {frac {m_{a}}{n_{a}}}cdot {frac {m_{b}}{n_{b}}}={frac {m_{a}cdot m_{b}}{n_{a}cdot n_{b}}}}
  4. Транзитивность отношения порядка. Для любой тройки рациональных чисел a, b и c {displaystyle (forall a,b,cin mathbb {Q} }) если a меньше b и b меньше c, то a меньше c, а если a равно b и b равно c, то a равно c.
    {displaystyle a<b,;b<c;Rightarrow a<c;;;;a=b,;b=c;Rightarrow a=c.}
  5. Коммутативность сложения. От перемены мест рациональных слагаемых сумма не меняется.
    forall a,bin {mathbb {Q}}~~a+b=b+a
  6. Ассоциативность сложения. Порядок сложения трёх рациональных чисел не влияет на результат.
    forall a,b,cin {mathbb {Q}}~~left(a+bright)+c=a+left(b+cright)
  7. Наличие нуля. Существует рациональное число 0, которое сохраняет любое другое рациональное число при суммировании.
    {displaystyle exists 0in mathbb {Q} :~forall ain mathbb {Q} ~~a+0=a}
  8. Наличие противоположных чисел. Любое рациональное число имеет противоположное рациональное число, при суммировании с которым даёт 0.
    {displaystyle forall ain mathbb {Q} ~exists left(-aright)in mathbb {Q} :~~a+left(-aright)=0}
  9. Коммутативность умножения. От перемены мест рациональных множителей произведение не меняется.
    forall a,bin {mathbb {Q}}~~acdot b=bcdot a
  10. Ассоциативность умножения. Порядок перемножения трёх рациональных чисел не влияет на результат.
    forall a,b,cin {mathbb {Q}}~~left(acdot bright)cdot c=acdot left(bcdot cright)
  11. Наличие единицы. Существует рациональное число 1, которое сохраняет любое другое рациональное число при умножении.
    {displaystyle exists 1in mathbb {Q} :~forall ain mathbb {Q} ~~acdot 1=a}
  12. Наличие обратных чисел. Любое ненулевое рациональное число имеет обратное рациональное число, умножение на которое даёт 1.
    {displaystyle forall ain mathbb {Q} ,;aneq 0~exists a^{-1}in mathbb {Q} :~~acdot a^{-1}=1}
  13. Дистрибутивность умножения относительно сложения. Операция умножения согласована с операцией сложения посредством распределительного закона:
    forall a,b,cin {mathbb {Q}}~~left(a+bright)cdot c=acdot c+bcdot c
  14. Связь отношения порядка с операцией сложения. К левой и правой частям рационального неравенства можно прибавлять одно и то же рациональное число.
    {displaystyle forall a,b,cin mathbb {Q} ~~a<bLeftrightarrow a+c<b+c}
  15. Связь отношения порядка с операцией умножения. Левую и правую части рационального неравенства можно умножать на одно и то же положительное рациональное число.
    {displaystyle forall a,b,cin mathbb {Q} ,;c>0:a<bLeftrightarrow acdot c<bcdot c}
  16. Аксиома Архимеда. Каково бы ни было рациональное число a, можно взять столько единиц, что их сумма превзойдёт a.
    {displaystyle forall ain mathbb {Q} ~exists nin mathbb {N} :~~sum _{k=1}^{n}1>a;;Longleftrightarrow ;forall ain mathbb {Q} ;exists nin mathbb {N} :n>a}

Дополнительные свойства[править | править код]

Все остальные свойства, присущие рациональным числам, не выделяют в основные, потому что они, вообще говоря, уже не опираются непосредственно на свойства целых чисел, а могут быть доказаны исходя из приведённых основных свойств или непосредственно по определению некоторого математического объекта. Таких дополнительных свойств очень много. Здесь имеет смысл привести лишь некоторые из них.

  • Отношение порядка «>» (с противоположным порядком аргументов) также транзитивно.
    {displaystyle forall a,b,cin mathbb {Q} :a>b,;b>cRightarrow a>c}
  • Произведение любого рационального числа на ноль равно нулю.
    forall ain {mathbb {Q}}~~acdot 0=0
  • Рациональные неравенства одного знака можно почленно складывать.
    {displaystyle forall a,b,c,din mathbb {Q} ~~a>b,;c>dRightarrow a+c>b+d}
  • Множество рациональных чисел mathbb {Q} является полем (а именно, полем частных кольца целых чисел mathbb {Z} ) относительно операций сложения и умножения дробей.
    left({mathbb {Q}},+,cdot right) — поле
  • В позиционной системе счисления рациональное число представляется периодической дробью. Более того, наличие представления в виде периодической дроби является критерием рациональности вещественного числа.
  • Каждое рациональное число является алгебраическим.
    {mathbb {Q}}subset {mathbb {A}}
  • Между любыми двумя различными рациональными числами a и b существует хотя бы одно рациональное число x, такое, что a<x и x<b. (В качестве примера такого числа можно взять x=textstyle {{frac {a+b}{2}}}.) Ясно, что между a и x, а также между x и b тоже существует хотя бы по одному рациональному числу. Отсюда следует, что между любыми двумя различными рациональными числами a и b существует бесконечно много рациональных чисел. Иначе говоря, не существует двух соседних рациональных чисел. В частности, не существует наименьшего положительного рационального числа.
  • Не существует наибольшего и наименьшего рационального числа. Для любого рационального числа x найдутся рациональные (и даже целые) числа a и b такие, что a<x и x<b.

Счётность множества рациональных чисел[править | править код]

Нумерация положительных рациональных чисел

Чтобы оценить количество рациональных чисел, нужно найти мощность их множества. Легко доказать, что множество рациональных чисел счётно. Для этого достаточно привести алгоритм, который нумерует рациональные числа, то есть устанавливает биекцию между множествами рациональных и натуральных чисел.
Примером такого построения может служить следующий простой алгоритм. Составляется бесконечная таблица обыкновенных дробей, на каждой i-ой строке в каждом j-ом столбце которой располагается дробь {frac {i}{j}}. Для определённости считается, что строки и столбцы этой таблицы нумеруются с единицы. Ячейки таблицы обозначаются left(i,jright), где i — номер строки таблицы, в которой располагается ячейка, а j — номер столбца.

Полученная таблица обходится «змейкой» по следующему формальному алгоритму.

Эти правила просматриваются сверху вниз и следующее положение выбирается по первому совпадению.

В процессе такого обхода каждому новому рациональному числу ставится в соответствие очередное натуральное число. То есть дроби 1/1 ставится в соответствие число 1, дроби 2/1 — число 2, и т. д. Нумеруются только несократимые дроби. Формальным признаком несократимости является равенство единице наибольшего общего делителя числителя и знаменателя дроби.

Следуя этому алгоритму, можно занумеровать все положительные рациональные числа. Это значит, что множество положительных рациональных чисел {mathbb {Q}}_{+} счётно. Легко установить биекцию между множествами положительных и отрицательных рациональных чисел, поставив в соответствие каждому рациональному числу противоположное ему. Таким образом множество отрицательных рациональных чисел {mathbb {Q}}_{-} тоже счётно. Их объединение {mathbb {Q}}_{+}cup {mathbb {Q}}_{-} также счётно по свойству счётных множеств. Множество же рациональных чисел {mathbb {Q}}={mathbb {Q}}_{+}cup {mathbb {Q}}_{-}cup left{0right} тоже счётно как объединение счётного множества с конечным.

Существуют и другие способы занумеровать рациональные числа. Например, воспользовавшись такими структурами как дерево Калкина — Уилфа, дерево Штерна — Броко или ряд Фарея.

Утверждение о счётности множества рациональных чисел может вызывать некоторое недоумение, так как на первый взгляд складывается впечатление, что оно гораздо обширнее множества натуральных чисел (ведь между любыми двумя натуральными числами находится бесконечное множество рациональных). На самом деле это не так, и натуральных чисел хватает, чтобы занумеровать все рациональные.

Недостаточность рациональных чисел[править | править код]

Гипотенуза такого треугольника не выражается никаким рациональным числом

В геометрии следствием так называемой аксиомы Архимеда (в более общем понимании, чем упомянуто выше) является возможность построения сколь угодно малых (то есть, коротких) величин, выражаемых рациональными числами вида 1/n. Этот факт создаёт обманчивое впечатление, что рациональными числами можно измерить вообще любые геометрические расстояния. Легко показать, что это не верно.

Из теоремы Пифагора известно, что гипотенуза прямоугольного треугольника выражается как квадратный корень суммы квадратов его катетов. Т. о. длина гипотенузы равнобедренного прямоугольного треугольника с единичным катетом равна {sqrt {2}}, то есть числу, квадрат которого равен 2.

Если допустить, что число {sqrt {2}} представляется некоторым рациональным числом, то найдётся такое целое число m и такое натуральное число n, что {sqrt {2}}={frac {m}{n}}, причём дробь {frac {m}{n}} несократима, то есть числа m и n — взаимно простые.

Если {sqrt {2}}={frac {m}{n}}, то 2={sqrt {2}}cdot {sqrt {2}}={frac {m}{n}}cdot {frac {m}{n}}={frac {m^{2}}{n^{2}}}, то есть m^{2}=2n^{2}. Следовательно, число m^{2} чётно, но произведение двух нечётных чисел нечётно, что означает, что само число m также чётно. А значит найдётся натуральное число k, такое что число m можно представить в виде m=2k. Квадрат числа m в этом смысле m^{2}=4k^{2}, но с другой стороны m^{2}=2n^{2}, значит 4k^{2}=2n^{2}, или n^{2}=2k^{2}. Как уже показано ранее для числа m, это значит, что число n — чётно, как и m. Но тогда они не являются взаимно простыми, так как оба делятся на 2. Полученное противоречие доказывает, что {sqrt {2}} не есть рациональное число.

Из вышесказанного следует, что существуют отрезки на плоскости, а, значит, и на числовой прямой, которые не могут быть измерены рациональными числами. Это приводит к возможности расширения понятия рациональных чисел до вещественных.

См. также[править | править код]

  • Дроби Фарея
  • Иррациональные числа
  • Непрерывная дробь

Примечания[править | править код]

  1. ↑ Рациональное число // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
  2. ↑ Шиханович Ю. А. Введение в современную математику (Начальные понятия). — М.: Наука, 1965. — С. 191. — 376 с.
  3. ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 30—31. — 672 с. — ISBN 5-482-00445-7.

Литература[править | править код]

  • И.Кушнир. Справочник по математике для школьников. — Киев: АСТАРТА, 1998. — 520 с.
  • П. С. Александров. Введение в теорию множеств и общую топологию. — М.: глав. ред. физ.-мат. лит. изд. «Наука», 1977
  • И. Л. Хмельницкий. Введение в теорию алгебраических систем
Источник

Приветствую Вас, уважаемые Читатели! Постоянному читателю моего канала конечно известно, что такое рациональные числа. Напомню, что это числа вида m/n, где m – целое, а n – натуральное число. Однако уже в древней Греции было известно, что есть и числа, которые нельзя представить в виде такой дроби.

Греки назвали их иррациональными, однако долгое время не удавалось построить их точную аксиоматику, определить эти самые “неразумные” (иррациональные) числа через арифметику “разумных”. Сделать это окончательно удалось лишь в 1858 году немецкому математику Рихарду Дедекинду в статье “Непрерывность и иррациональные числа”. Причем вышло у него всё настолько тривиально и одновременно красиво, что грех этим не поделиться. Поехали!

Источник: https://www.thefamouspeople.com/profiles/images/richard-dedekind-3.jpg
Источник: https://www.thefamouspeople.com/profiles/images/richard-dedekind-3.jpg

Сам Дедекинд был очарован идеей выразить иррациональные числа как следствие “простейшего арифметического акта – счёта, который представляет собой последовательное представление бесконечного ряда положительных целых чисел, каждое из которых определяется числом, ему предшествующим”. Со сложением и умножением таких чисел проблем не было : каждый результат этих операций являл собой число из этого ряда.

Возьмем все натуральные числа. Сложив 5 и 7 мы получим число 12 из того же класса. Умножим 5 на 7 получим 35 – число тоже натуральное.

Однако с вычитанием и делением ситуация проблема. Определив вычитание (например, 5 – 7 = -2 – число из другой “вселенной”, относительно натуральных) , мы дополнили натуральные числа отрицательными, выделив класс целых чисел. Операция деления (5/7 – на пальцах не посчитать) заставила ввести и рациональные числа. Выбросив из них 0, математики “замкнули круг”, определив поле рациональных чисел R, замкнутое относительно четырех арифметических операций.

Что мы знаем об этом поле? В нём существуют понятные каждому законы:

1. Если число a > b, b > c, то a > c. На числовой прямой, иначе говоря, это будет значить, что b лежит между a и c.

2. Если a и b различные числа, то между ними существует бесконечное количество других чисел.

Без потери общности можно рассматривать только положительные рациональные числа
Без потери общности можно рассматривать только положительные рациональные числа

3. Если a – есть рациональное число, то все числа в R распадаются на два класса: те, которые на числовой прямой лежат слева от а (класс А2) и те, которые лежат справа от a (класс А1). Для каждого числа из класса А1 известно, что оно меньше числа из класса А2:

Важно добавить, что число a является наибольшим элементом в A1 либо в наименьшим в A2.
Важно добавить, что число a является наибольшим элементом в A1 либо в наименьшим в A2.

Само число а можно произвольно отнести к первому или второму классу, но самые важный вывод в том, что получено определение рационального числа а как сечения (A1, A2). С другой стороны понятно, что каждое заданное таким образом сечение определяет натуральное число.

Но есть ли сечения, которые не могут быть проведены рациональными числами? Конечно, и их бесконечное количество. Самый простой пример – это √2, совершивший революцию в восприятии числовой прямой, ставший удивительным подтверждением её непрерывности и подтвердивший, что между рациональными числами есть пробелы.

Источник: https://upload.wikimedia.org/wikipedia/commons/0/0e/Dedekind_cut-_square_root_of_two.png
Источник: https://upload.wikimedia.org/wikipedia/commons/0/0e/Dedekind_cut-_square_root_of_two.png

На самом деле, сечение, производимое √2 имеет значительные различия от сечений, которые производят рациональные числа. Например, в классе А1 (красный цвет) нет наибольшего числа: мы сколько угодно можем приближать к √2 слева, применяя всё более точные рациональные дроби, но никогда не найдем “того самого наибольшего”. Такая же ситуация и справа: для класса А2 (синий цвет) никогда не найти “наименьшего” в мире рациональных чисел.

Тогда Дедекинд постановил: всегда, когда мы будем встречаться с сечением такого вида, мы будем понимать под ним иррациональное число.

Таким образом, мы закрываем всю вещественную прямую плотным слоем рациональных и иррациональных чисел, а доопределив среди них отношение порядка и арифметические операции, порождаем совокупный класс вещественных чисел, каждое из которых может быть приближено рациональными числами с любой точностью.

Ценность теории Дедекинда в том, что им на основе наглядных геометрических соображений была выявлена сущность непрерывности – центрального понятия математического анализа, которое раньше использовали, ссылаясь на очевидность.

Сочинение Дедекинда до сих пор остается одним из самых доступных изложений теории вещественных чисел. Следующая попытка – уже не геометрическая, а конструктивная. Произойдет она почти через 24 года, а её автором будем “гений бесконечности” Георг Кантор. Но это – уже совсем другая история. Спасибо за внимание!

Читайте также:

Источник

$begingroup$

I was absent from my Analysis Class for a couple days, and I’m a bit confused as to how to solve this problem… any help would be appreciated!

Does there exist a smallest possible rational number?
Given a real number x, does there exist a smallest real number y > x?

From C.C Pugh – Real Mathematical Analysis

  • real-analysis

asked Feb 10, 2015 at 2:07

Maria Sanchez's user avatar

$endgroup$

8

  • $begingroup$
    I think you’ve asked two different questions. Pay careful attention to the use of ‘rational’ and ‘real’
    $endgroup$

    Feb 10, 2015 at 2:08

  • $begingroup$
    Given a positive rational number, you can always divide by two to get a smaller one.
    $endgroup$

    Feb 10, 2015 at 2:08

  • $begingroup$
    Do you understand the problem? Think of any rational number (say, $-5/12$), is there any rational number that is less than the number you thought of? Apply the same reasoning to the other question.
    $endgroup$

    Feb 10, 2015 at 2:08

  • $begingroup$
    Make sure you talk to your professor; they more than anybody will be able to help you catch up.
    $endgroup$

    Feb 10, 2015 at 2:09

  • $begingroup$
    Note that $n+1 > n$, so what is the relationship between $1/n$ and $1/(n+1)$? What does this tell you about rational numbers in general?
    $endgroup$

    Feb 10, 2015 at 2:09

You must log in to answer this question.

Источник

Данная статья посвящена изучению темы “Рациональные числа”. Ниже приведены определения рациональных чисел, даны примеры, рассказано о том, как определить, является ли число рациональным, или нет. 

Рациональные числа. Определения

Прежде чем дать дефиницию рациональных чисел вспомним, какие еще есть множества чисел, и как они связаны между собой. 

Натуральные числа, в совокупности с противоположными им и числом ноль образуют множество целых чисел. В свою очередь, совокупность целых дробных чисел образует множество рациональных чисел.

Определение 1. Рациональные числа

Рациональные числа – числа, которые можно представить в виде положительной обыкновенной дроби ab, отрицательной обыкновенной дроби -ab или числа ноль. 

Таким образом, можно оставить ряд свойств рациональных чисел:

  1. Любое натуральное число является рациональным числом. Очевидно, каждое натуральное число n можно представить в виде дроби 1n.
  2. Любое целое число, включая число 0, является рациональным числом. Действительно, любое целое положительное и целое отрицательное число легко представляется в виде соответственно положительной или отрицательной обыкновенной дроби. Например, 15=151, -352=-3521.
  3. Любая положительная или отрицательная обыкновенная дробь ab является рациональным числом. Это следует напрямую из данного выше определения.
  4. Любое смешанное число является рациональным. Действительно, ведь смешанное число можно представить в виде обыкновенной неправильной дроби.
  5. Любую конечную или периодическую десятичную дробь можно представить в виде обыкновенной дроби. Поэтому, каждая периодическая или конечная десятичная дробь является рациональным числом. 
  6. Бесконечные и непериодическое десятичные дроби не являются рациональными числами. Их невозможно представить в форме обыкновенных дробей.

Приведем примеры рациональных чисел. Числа 5, 105, 358, 1100055 являются натуральными, положительными и целыми. Сдедовательно, это рациональные числа. Числа -2, -358, -936 представляют собой целые отрицательные числа, и они также рациональны в соответствии с определением. Обыкновенные дроби 35, 87, -358 также являются примерами рациональных чисел.  

Приведенное выше определение рациональных чисел можно сформулировать более кратко. Еще раз ответим на вопрос, что такое рациональное число.

Определение 2. Рациональные числа

Рациональные числа – это такие числа, которые можно представить в виде дроби ±zn, где z – целое число, n – натуральное число.

Можно показать, что данное определение равносильно предыдущему определению рациональных чисел. Чтобы сделать это, вспомним, что черта дроби равносильна знаку деления. С учетом правил и свойств деления целых чисел, можно записать следующие справедливые неравенства:

0n=0÷n=0; -mn=(-m)÷n=-mn.

Таким образом, можно записать:

zn=zn, при z>00, при z=0-zn, при z<0

Собственно, данная запись и является доказательством. Приведем примеры рациональных чисел, основываясь на втором определении. Рассмотрим числа -3, 0, 5, -755, 0,0125 и -135. Все эти числа являются рациональными, так как  их можно записать в виде дроби с целым числителем и натуральным знаменателем: -31, 01,-755, 12510000, 85.

Приведем еще одну эквивалентную форму определения рациональных чисел.

Определение 3. Рациональные числа

Рациональное число – это такое число, которое можно записать в виде конечной или бесконечной периодической десятичной дроби.

Данное определение напрямую следует из самого первого определения этого пункта. 

Подведем итог и сформулируем резюме по данному пункту:

  1. Положительные и отрицательные дробные и целые числа составляют множество рациональных чисел.
  2. Каждое рациональное число можно представить в виде обыкновенной дроби, числитель которой является целым числом, а знаменатель – натуральным числом.
  3. Каждое рациональное число можно также представить в виде десятичной дроби: конечной или бесконечной периодической.

Какое из чисел является рациональным?

Как мы уже выяснили, любое натуральное число, целое число, правильная и неправильная обыкновенная дробь, периодическая и конечная десятичная дробь являются рациональными числами. Вооружившись этими знаниями можно без труда определить, является ли какое-то число рациональным.

Однако на практике часто приходится иметь дело не с числами, а с числовыми выражениями, которые содержат корни, степени и логарифмы. В некоторых случаях ответ на вопрос “рационально ли число?” является далеко не очевидным. Рассмотрим методы ответа на этот вопрос.

Если число задано в виде выражения, содержащего только рациональные числа и арифметические действия между ними, то результат выражения – рациональное число.

Например, значение выражения 2·318-0,250,(3) является рациональным числом и равно 18. 

Таким образом, упрощение сложного числового выражения позволяет определить, рационально ли заданное им число.

Теперь разберемся со знаком корня.

Оказывается, что число mn, заданное в видя корня степени n от числа m рационально лишь тогда, когда m является n-ой степенью какого-то натурального числа.

Обратимся к примеру. Число 2 не является рациональным. Тогда как 9, 81 – рациональные числа. 9 и 81 – полные квадраты чисел 3 и 9 соответственно. Числа 199, 28, 151 не являются рациональными числами, так как числа под знаком корня не являются полными квадратами каких-либо натуральных чисел. 

Теперь возьмем более сложный случай. Является ли рациональным число 2435? Если возвести 3 в пятую степень, получается 243, поэтому исходное выражение можно переписать так: 2435=355=3. Следовательно, данное число рационально. Теперь возьмем число 1215. Это число нерационально, так как не существует натурального числа, возведение которого в пятую степень даст 121.

Для того, чтобы узнать, является ли логарифм какого-то числа a по основанию b рациональным числом необходимо применить метод от противного. К примеру, узнаем, рационально ли число log25. Предположим, что данное число рационально. Если это так, то его можно записать в виде обыкновенной дроби log25=mn.По свойствам логарифма и свойствам степени справедливы следующие равенства:

5=2log25=2mn5n=2m

Очевидно, последнее равенство невозможно так как в левой и правой частях находятся соответственно нечетное и четное числа. Следовательно, сделанное предположение неверно, и число log25 не является рациональным числом.

Стоит отметить, что при определении рациональности и иррациональности чисел не стоит принимать скоропостижных решений. Например, результат произведения иррациональных чисел не всегда является иррациональным числом. Наглядный пример: 2·2=2.

Также существуют иррациональные числа, возведение которых в иррациональную степень дает рациональное число. В степени вида 2log23 основание и показатель степени являются иррациональными числами. Однако само число является рациональным: 2log23=3.

Источник

Понятие дроби  и
положительного рационального числа.

Множество
положительных рациональных чисел, его свойства.

Исторически появление дробей связано с
измерением величин. Рассмотрим задачу, которая иллюстрирует необходимость
появления дробных чисел.

                        а

|——●——-|——●——-|——●|                   

|——●——-|               

   e1

      е

Решим практическую задачу по измерению длины
отрезка а меркой е.

Для этого отложим е на отрезке а. Видим, что
длина отрезка а больше, чем 2е, но меньше, чем 3е.            (2e < a < 3e)

Среди натуральных чисел нет числа, которое бы
соответствовало длине отрезка а при  измерении его  меркой е.  Тогда, измеряя
длину отрезка а другой меркой е1 , такой, что е = 2е1
получим а = 5е1 .

Вернёмся к первоначальному измерению отрезка
меркой е.

е1 = е/2 = ½ е

а= 5 • е1 =5 •
½ е = 5/2 е

а= 5/2 е

Получили дробное число 5/2, так как при
измерении отрезка а меркой е мы использовали 2 натуральных числа 5 и 2.

В общем виде понятие дроби определяется
 так:

 Пусть даны отрезок а и единичный отрезок
е, причём отрезок е является суммой   n  отрезков,
равных е1. Если  отрезок
а состоит из m отрезков, равных е1    то
его длина может быть представлена в виде  m
/n • е.

Символ m /n
 называется дробью, где числа  m    и   
n  являются
натуральными числами.

т.е. е =n
• е1     ,    а = m • е1 , , тогда => то а= m /n • е

Вернёмся к рассмотренной выше задаче и снова
сделаем чертёж.

                   a

|——●——-|——●——-|——●|                   

|——●——-|               

   e1

         2 е1 =
е

         4 е2 =
е

         8 е3 =
е

а =  5/2 е = 10/4 е  = 20/8 е   и т.д.

Этот процесс можно продолжать бесконечно, при
этом мы будем получать новые дроби, которые выражают длину одного и того же
отрезка.

Опр. 1 Дроби,
выражающие длину одного и того же отрезка при единице длины  е,
называются равными дробями.

Теорема   
(Признак равенства дробей)

Для того чтобы дроби m /n   и  p /q  были равны,
необходимо и достаточно, чтобы m • q   = n • p  

m /n   = p /q  <=> m
• q   = n • p  

 Доказательство:

1.     
Необходимость (прямая
теорема)

Дано: m /n   = p /q  (m, n, p, q Π N)

Доказать:  m • q   = n • p .

Доказательство: m /n   = m q  /n q  (“q Π N)

p /q  = p n   / q  n     (“n Π N)

Из равенства дробей    m /n   = p /q  (по условию) => равенство
дробей

m q  /n q = p n   / q  n     , из которого, в свою очередь следует,
что

m • q   = n • p  (из равенства дробей с равными знаменателями
следует, что равны числители).

2. Достаточность.

Дано:  m • q   = n • p  

Доказать:  m /n   = p /q 

Доказательство:
разделим обе части истинного равенства m • q   = n • p  

на натуральное число n q,
получим истинное равенство m q  /n q = n  p /  n  q.

Но m q  /n q = m /n   , а n  p /  n  q = p /q   =>
 m /n   = p /q 

Из этого признака вытекает основное
свойство дроби:

Если числитель и знаменатель дроби умножить
или разделить на одно и то же натуральное число, то получится дробь, равная
данной.

 Опр: Сокращение
дробей – это замена данной дроби другой, равной данной, но с меньшим
числителем и знаменателем.

Если числитель и знаменатель делятся только на
единицу, то есть являются числами взаимнопростыми, то дробь называется
несократимой.

Из этого свойства следует правило
сокращения дробей:

Сократить дробь – это значит заменить дробь
другой дробью, равной данной, но с меньшим числителем и знаменателем.

Опр: Приведение
дробей к общему знаменателю – это замена дробей равными им дробями,
имеющими одинаковые знаменатели.

Общим знаменателем двух дробей m /n    и  p /q  является общее
кратное чисел n и  q  , а наименьшим
общим знаменателем – НОК (n,  q)

Понятие
положительного рационального числа

Опр. 1.  Положительным рациональным числом
называется множество равных дробей, а каждая дробь этого множества называется
записью положительного рационального числа.

Например,  {1/2, 2/4, 3/6, 4/8, …} или {1/3, 2/6, 3/9, 4/12, …}.

Это примеры положительных
рациональных чисел. Дробь 2/4 или 3/6 – это различные записи одного и того же
положительного рационального числа.

Т.о. положительное
рациональное число и дробь – это разные понятия, но часто мы эти понятия
отождествляем для упрощения речи.

Вывод: Для любого положительного рационального числа
существует единственная несократимая дробь, которая является записью этого
числа.

Например, в первом числе ½, во втором числе 1/3.

Множество положительных
рациональных чисел обозначается символом Q+ .

Это множество бесконечно.
Можно показать, что множество натуральных чисел является подмножеством
множества положительных, рациональных чисел, например, 2 = 2/1.

Упорядоченность
множества положительных рациональных чисел

Рассмотрим отношения
«больше», «меньше», «равно» на множестве положительных рациональных чисел.

Если рациональное число а
представлено дробью 2/5, а рациональное число в – дробью 4/10, то а = в, так
как 2/5 = 4/10 (по правилу сокращения дробей).

Как узнать, какое из
рациональных чисел а и в меньше (больше)?

Определение. Пусть а и в – положительные рациональные
числа. Тогда а меньше в    (а < в), если существует такое положительное
рациональное число с, что а + с =в.

Это определение позволяет
сформулировать необходимое и достаточное условие существования разности во множестве
Q+.

Необходимое и достаточное условие существования разности во
мн-ве Q+.

Для того чтобы
разность положительных рациональных чисел а и в существовала, необходимо и
достаточно, чтобы в < а.

Если
a = m/ n,     b = p/ q, то а <  в 
тогда и только тогда, когда

1.
Если n=
q,  то
а <  в  тогда и только тогда, когда m < p .

2.
Если n ≠ q  то а
<  в  тогда и только тогда, когда m q < np .

Пример.
а = 5/11           в = 7/13               5•13 < 7•11,  65< 77

Отношение «меньше»
транзитивно и антисимметрично, то есть является отношением порядка на множестве
Q+, а само множество является упорядоченным.

Во
множестве натуральных чисел выполняются свойства:

1).
Существует наименьшее натуральное число -1.

2)
Каждое последующее число на 1 больше предыдущего.

3)
Множество N дискретно – между двумя соседними натуральными числами нет другого
натурального числа.

Во
множестве положительных рациональных чисел выполняются свойства:

1).
Нет наименьшего числа.

2)
Между любыми двумя различными положительными рациональными  числами заключено
бесконечно много чисел множества Q+.

Докажем 1 свойство.

Методом от противного. Пусть дробь m /n – наименьшее положительное
рациональное число. Образуем новое число m /n+1.

m /n > m /n+1,
тогда  m • (n+1)
> m • n, то есть нашлось такое
положительное рациональное число, которое меньше, чем m/n    => наше предположение неверно, нет наименьшего положительного
рационального числа.

Проиллюстрируем 2 свойство на примере.

Возьмём два рациональных числа 1/3    и 2/3. Найдём число,
которое будет являться средним арифметическим данных чисел.

Для этого (1/3 + 2/3) : 2 = 3/3 : 2 = 1: 2 = 1/2                   => 1/3 < ½  <   2/3  

 Существуют ещё числа между 1/3 и 2/3. для этого найдём
среднее арифметическое чисел 1/3 и ½. Получим 5/12.    1/3 < 5/12 < ½
<  2/3, то есть можно найти множество положительных рациональных чисел
между  двумя данными числами.

Вывод: Множество
положительных рациональных чисел плотно в себе, а свойство называется свойством
плотности.

Источник

Добавить комментарий