Как найти наименьшее значение функции без графика

Наибольшее и наименьшее значение функции

Все для самостоятельной подготовки к ЕГЭ

Зарегистрироваться

Русский язык
Математика (профильная)
Математика (базовая)
Обществознание
Физика
История
Биология
Химия
Английский язык
Литература
Информатика
География

Задания
Варианты
Теория

Простейшие уравнения
Вычисления и преобразования. Логарифмические выражения
Логарифмические уравнения
Начала теории вероятностей
Вычисления и преобразования выражений
Тригонометрия. Основные тождества и формулы приведения
Тригонометрия. Преобразование выражений
Тригонометрия. Простейшие уравнения
Планиметрия. Четырехугольники
Планиметрия. Задачи на окружности
Планиметрия. Вписанная и описанная окружность
Производная. Дифференцирование, физический смысл производной
Производная. Геометрический смысл
Производная. Производная сложной функции
Производная. Исследование функции
Задачи с прикладным содержанием
Текстовые задачи. Задачи на движение
Текстовые задачи. Проценты, совместная работа
Текстовые задачи. Смеси и сплавы, прогрессии
Стереометрия. Параллелепипед. Пирамида. Призма
Стереометрия. Цилиндр. Конус. Шар
Стереометрия. Комбинация тел
Тригонометрические уравнения
Уравнения
Стереометрия
Стереометрия.

Нахождение расстояний и углов
Метод интервалов
Метод рационализации
Задачи на многоугольники
Задачи на комбинацию окружностей и многоугольников
Оптимизация
Графический метод
Уравнение окружности
Плоскость xOa
Расположение корней, теорема Виетта
Другие задачи с параметром
Числа и их свойства
Планиметрия. Треугольники
Теоремы о вероятностях событий

Разбор сложных заданий в тг-канале:

Посмотреть

Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.

Чтобы найти наибольшее или наименьшее значение функции необходимо:

1. Найти производную функции $f'(х)$
2. Найти стационарные точки, решив уравнение $f'(х)=0$
3. Проверить, какие стационарные точки входят в заданный отрезок.
4. Вычислить значение функции на концах отрезка и в стационарных точках из п.3
5. Выбрать из полученных результатов наибольшее или наименьшее значение.

Чтобы найти точки максимума или минимума необходимо:

1. Найти производную функции $f'(х)$
2. Найти стационарные точки, решив уравнение $f'(х)=0$
3. Разложить производную функции на множители.
4. Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
5. Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.

Таблица производных некоторых элементарных функций:

Функция	Производная
$c$	$0$
$x$	$1$
$x^n, n∈N$	$nx^{n-1}, n∈N$
${1}/{x}$	$-{1}/{x^2}$
${1}/x{^n}, n∈N$	$-{n}/{x^{n+1}}, n∈N$
$√^n{x}, n∈N$	${1}/{n√^n{x^{n-1}}, n∈N$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	${1}/{cos^2x}$
$ctgx$	$-{1}/{sin^2x}$
$cos^2x$	$-sin2x$
$sin^2x$	$sin2x$
$e^x$	$e^x$
$a^x$	$a^xlna$
$lnx$	${1}/{x}$
$log_{a}x$	${1}/{xlna}$

Основные правила дифференцирования

1. 2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))′=f′(g(x))∙g′(x)$

Пример:

$f(x)= cos(5x)$

$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$

Пример:

Найдите точку минимума функции $y=2x-ln⁡(x+11)+4$

Решение:

1. Найдем ОДЗ функции: $х+11>0; х>-11$

2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$

3. Найдем стационарные точки, приравняв производную к нулю

${2x+21}/{x+11}=0$

Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю

$2x+21=0; x≠-11$

$2х=-21$

$х=-10,5$

4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.

$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$

5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума. 3-5=6-90-5= -89$

Наибольшее значение равно $967$

Ответ: $967$

Практика: решай 12 задание и тренировочные варианты ЕГЭ по математике (профиль)

Составим твой персональный план подготовки к ЕГЭ

Нахождение наибольшего и наименьшего значения функции — пример

Поможем понять и полюбить математику

Начать учиться

Функции и графики в математике — темы, которые не могут оставить равнодушными никого. Ученики, а порой даже учителя, делятся на два враждующих лагеря: тех, кто ненавидит этот раздел, и тех, кому он кажется проще таблицы умножения. Истина где-то посередине: функции требуют нашего особого внимания, но способны подчиниться любому, кто знает правильные алгоритмы. Давайте и мы попробуем приручить их!

В этой статье мы разберём нахождение наибольшего и наименьшего значения функции на отрезке, интервале, в
бесконечности, а также повторим основные свойства функции и связанные термины.

Что такое функция

Наш мир — это огромная коллекция взаимосвязей, которые порой явно, а порой невидимо влияют на всех, кто в них
участвует. Ваше настроение может влиять на успеваемость в школе, питание — на спортивные достижения, навыки — на
возможность поступить в университет. В физическом мире температура влияет на скорость протекания процесса,
плотность тела — на его способность к плаванию в воде, угол падения лучей — на то, каким образом они будут преломляться, пройдя
через прозрачную призму.

Некоторые из этих взаимоотношений можно описать математически: обозначить участников буквами латинского алфавита и
описать их взаимосвязь через математические действия и знаки.

Функция — это правило, формула или выражение, которое описывает взаимосвязь двух величин.

Как описать зависимость пройденного пути от времени?

Есть ли правило, которое описывает отношение ускорения тела и силы, приложенной к нему? Да:

А что, если нужно вычислить зависимость остатка денег от количества купленных товаров? Пожалуйста:

, где

— остаток денег,

— исходная сумма,

— количество товара,

— стоимость товара за одну единицу.

В каждом из этих выражений есть зависимая и независимая переменные. Зависимая переменная — это и есть функция, а
независимая — аргумент. Так, в нашем последнем примере стоимость товара за одну его единицу
является независимой переменной (цену назначил продавец, и мы на это повлиять никак не можем). Зато остаток в
кошельке поддаётся изменениям — чем меньше мы купим товара, тем больше останется денег. И так в любой зависимости!

Обратите внимание

Зависимая переменная стоит слева от знака «равно» и определяется через выражение, содержащее аргумент.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Графическое задание функции

Представьте, что для школьной научной конференции вы готовите доклад о загрязнении окружающей среды. Как вы
думаете, что произведёт больший эффект на аудиторию:

• перечисление статистических данных об увеличении количества мусора за последний год;

• наглядная демонстрация роста загрязнений в виде графика?

Верно — иллюстрации, фотографии, графики и диаграммы говорят порой громче любых слов! 📈

Для наглядного отображения зависимости одной переменной от другой мы введём систему координат, в которой построим график.
График — это прямая, кривая или ломаная линия, которая была построена чётко по уравнению
(функции).

Как мы уже говорили, функция состоит из зависимой и независимой переменной. В декартовой системе координат
независимая переменная отображается с помощью оси
зависимая — с помощью оси

В зависимости от типа функции график может выглядеть, например, так:

Наибольшее и наименьшее значение функции

На уроках алгебры учитель просит определить наибольшее и наименьшее значение функции. Что он имеет в виду?

Чтобы найти наименьшее или наибольшее значение функции, необходимо понять, какое наименьшее или наибольшее
численное значение принимает — зависимая переменная.

Наибольшее значение функции на некотором промежутке — это значение которое при любом значении делает справедливым неравенство

Теперь расшифровка! 😅 Если на данном интервале значение больше, чем значение в окрестностях точки то такой будет считаться наибольшим значением на данном промежутке.

Наименьшее значение функции на некотором промежутке — это значение которое при любом значении делает справедливым неравенство

Если на данном интервале значение меньше, чем значение в окрестностях точки то такой будет считаться наименьшим значением на данном промежутке.

Наибольшее и наименьшее значение функции на графиках

Самый простой способ определить и — рассмотреть график.

Если заданный интервал представлен прямой:

• при возрастающей функции: наименьшее значение функция примет при наименьшем аргументе и наоборот, наибольшее
  значение функции будет соответствовать наибольшему значению аргумента;

• при убывающей функции: наименьшее значение функция примет при наибольшем аргументе и наоборот, наибольшее
  значение функции будет соответствовать наименьшему значению аргумента.

Если заданный интервал представлен кривой:

• максимальное значение функции выглядит как вершина горы, возвышенности, тогда как минимальное значение мы
  можем определить как самую низкую точку относительно этого пика;

• минимальное значение функции выглядит как дно низины, оврага, тогда как максимальное значение мы можем
  определить как самую высокую точку относительно этого пика.

Возможен и такой вариант, когда горы и овраги встречаются на одном промежутке — тогда мы просто объединяем оба
пункта для нахождения и Помним главное правило: максимальное значение функции всегда представлено самой
высокой точкой относительно оси минимальное значение функции — самой низкой точкой.

Определение наименьшего и наибольшего значения через производную

Удобен ли способ нахождения и через график? Определённо!
Всегда ли его можно использовать? К сожалению, нет.

Дело в том, что большинство заданий в алгебре на эту тему даются не через график, а через уравнение функции.
Зачастую эти функции сложные, и построение их графиков займёт время. Ошибётесь в построении — допустите ошибку и в
нахождении максимального и минимального значения, а нам это не нужно.

Способ, который не уступает первому в простоте и лаконичности, заключается в определении производной функции и
поиске стационарных точек. Кажется, нам встретились два новых термина — давайте их разберём.

Производная функции — это отношение приращения функции к приращению аргумента при бесконечно
малом приращении аргумента.

Производная функции показывает, как быстро увеличивается функция при бесконечно малом увеличении

По сути, найти производную означает провести определённые действия с помощью таблицы производных
функций. Обязательно загляните в нашу статью об этом и изучите материал, а мы пока пойдём дальше.

Стационарная точка — точка, в которой значение аргумента производной функции равно нулю.

Дело в том, что по теореме Ферма в стационарных точках определяется экстремум функции, поэтому можно сделать
вывод, что на некотором промежутке в них можно определить и наибольшее/наименьшее значение функции.

Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке

Как определить наибольшее и наименьшее значения функции на отрезке?

1. Найдём область определения данной функции и проверим, входит ли в неё заданный отрезок.

2. Найдём производную данной функции.

3. Приравняем производную к нулю и найдём точки, в которых она обращается в нуль (решим уравнение).

4. Выберем из корней уравнения те точки, которые попадают в заданный промежуток, и вычислим значение функции в
   них.

5. Возьмём точки начала и конца отрезка и найдём значение функции в них.

6. Сделаем вывод о наибольшем и наименьшем значении функции.

Разберём пару примеров.

Задача 1

Найдите наибольшее и наименьшее значение функции на отрезке

Решение:

1. ОДЗ:

4. не попадает в промежуток Найдём значение функции только в крайних точках:

5. Тогда является наименьшим значением на данном отрезке, а наибольшим.

Задача 2

Найдите наибольшее и наименьшее значение функции на отрезке

Решение:

1. ОДЗ:

3. , но в таком случае знаменатель равен нулю, что невозможно. А значит, производная
   не обращается в нуль, стационарных точек нет.

4. Найдём значение функции в крайних точках отрезка:

   — точка максимума на промежутке;

   — точка минимума на промежутке.

Наименьшее и наибольшее значение функции на открытом или бесконечном интервале

В чём отличие отрезка от интервала? В отрезке определены крайние точки, в интервале же крайние точки могут не
существовать (например ), или значение функции в них мы рассматривать не будем (на интервале
мы рассмотрим значение функции в окрестностях этих точек, но не в них самих).

Вариантов задания интервала может быть множество, но каждый из них сведёт определение
и к поиску производной и вычислению пределов в крайних точках, например
и

Вернёмся на пару шагов назад. А что такое предел функции?

Если говорить коротко, то предел функции — это такое число , к которому функция стремится, в то время как аргумент стремится достичь числа

Предположим, наша функция представлена уравнением Найдём предел функции при подставив это значение вместо в уравнение:

Это означает, что функция стремится приблизиться к числу в то время как аргумент тоже приближается к этому значению. В отрыве от настоящего
уравнения мы могли бы представить это так:

Функция может стремиться не только к рациональному
числу, но также и к бесконечности. В таком случае при подстановке бесконечности в функцию возникает
неопределённость, которую необходимо решить разными методами.

В рамках этой статьи мы не можем посвятить этому много времени, поэтому ждём Вас на курсах математики в онлайн-школе
Skysmart — там ни один предел не останется незамеченным. 😉

Вернёмся к функции! Итак, как же определить наибольшее и наименьшее значение на интервале?

1. Найдём область определения данной функции и проверим, входит ли в неё заданный интервал.

2. Найдём производную данной функции.

3. Приравняем производную к нулю и найдём точки, в которых она обращается в нуль (решим уравнение).

4. Выберем из корней уравнения те точки, которые попадают в заданный промежуток, и вычислим значение функции в
   них.

5. Возьмём крайние точки интервала и вычислим значение предела в этих точках (согласно типу интервала).

6. Сделаем вывод о наибольшем и наименьшем значении функции.

Для вычисления предела вам поможет сводная таблица, которая учитывает вид интервала:

Интервал	Предел
	и
	и
	и

Если при вычислении одностороннего предела вы получаете бесконечность, то вычислить наибольшее/наименьшее
значение невозможно.

Задача 3

Необходимо найти наибольшее и наименьшее значение функции на всём промежутке области определения.

Решение:

1. ОДЗ:

3. Найдём стационарные точки:

4. Точка
   входит в промежуток области определения и является точкой минимума.

5. Так как
   — парабола, ветви которой направлены вверх, мы не можем определить точку
   максимума.

Cегодня мы на славу потрудились и разобрали множество важных вопросов:

• что такое функция, какой она бывает;

• что такое наименьшее и наибольшее значение функции;

• как определить и на отрезке;

• как находить наименьшее и наибольшее значение функции на интервале;

• что такое предел и производная.

Вот и ещё одна тема по математике стала понятнее! А если всё же остались вопросы, спешим ещё раз пригласить вас на уроки математики в Skysmart — мы постараемся ответить на них, закрепить материал и попрактиковаться в решении задач. Обещаем, будет увлекательно и безумно интересно!

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Дарья Вишнякова

К предыдущей статье

Вектор

К следующей статье

Вычисление первообразной функции

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

5.1 Максимум и минимум

точка локального максимума на функции является
точка $(x,y)$ на графике функции, координата $y$ которой равна
больше, чем все остальные координаты $y$ на графике в точках «близких
к»$(x,y)$. Точнее, $(x,f(x))$ является локальным максимумом, если существует
интервал $(a,b)$ с $allocal точкой минимума
если он имеет локально наименьшую координату $y$. Снова
точнее: $(x,f(x))$ является локальным минимумом, если существует
интервал $(a,b)$ с $локальным экстремумом
является либо локальным минимумом, либо локальным максимумом.

Локальные точки максимума и минимума хорошо различаются на графике
функцию, и поэтому полезны для понимания формы
график. Во многих прикладных задачах мы хотим найти наибольшее или
наименьшее значение, которое достигает функция (например, мы можем захотеть
найти минимальную стоимость, при которой может быть выполнена некоторая задача) и, следовательно,
определение максимальных и минимальных точек будет полезно для прикладных
также проблемы. Некоторые примеры точек локального максимума и минимума
показаны на рис. 5.1.1.

Рисунок 5.1.1. Некоторые локальные точки максимума ($A$) и точки минимума ($B$).

Если $(x,f(x))$ — точка, в которой $f(x)$ достигает локального максимума или минимума,
и если производная от $f$ существует в точке $x$, то граф имеет
касательная, а касательная должна быть горизонтальной.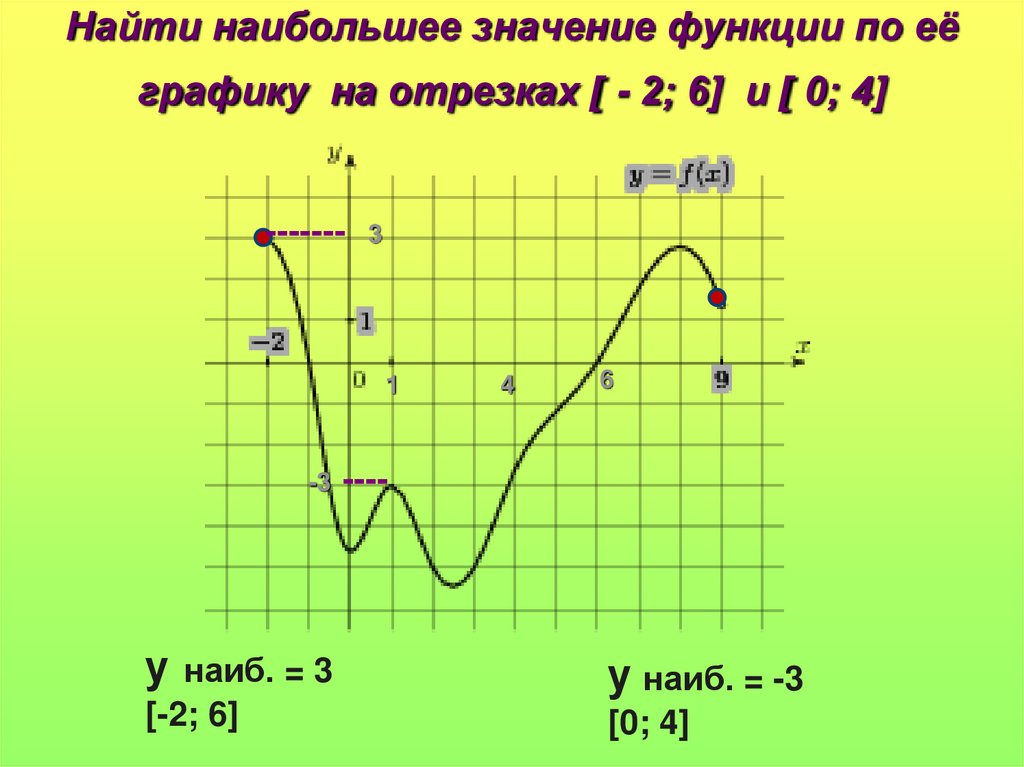 Это
достаточно важно, чтобы сформулировать его как теорему, хотя мы не будем его доказывать.

Теорема 5.1.1 (теорема Ферма). Если $f(x)$ имеет локальный экстремум в точке $x=a$ и
$f$ дифференцируема в $a$, тогда $f'(a)=0$.
$qed$

Таким образом, единственный
точки, в которых функция может иметь локальный максимум или минимум
точки, в которых производная равна нулю, как на левом графике в
рисунок 5.1.1,
или производная не определена, как на правом графике. Любое значение
$x$, для которых $f'(x)$ равно нулю или не определено, называется
критическое значение для $f$ и
точка $(x,f(x))$ на кривой называется
критическая точка для $f$.
При поиске точек локального максимума и минимума вы, вероятно,
сделать два вида ошибок: вы можете забыть, что максимум или минимум
может произойти там, где производная не существует, и поэтому забудьте проверить
везде ли существует производная. Вы также можете предположить, что
любое место, где производная равна нулю, является локальным максимумом или минимумом
точка, но это не так. 2$ и $f'(0)=0$, но нет ни максимума, ни
минимум в $(0,0)$.

Рисунок 5.1.2. Нет ни максимума, ни минимума, хотя производная равна нулю.

Поскольку производная равна нулю или не определена как в локальном максимуме, так и в
точки локального минимума, нам нужен способ определить, какие из них
на самом деле происходит. Большинство
элементарный подход, но часто утомительный или трудный, состоит в том, чтобы
непосредственно проверить, находится ли координата $y$ «близко» к потенциальному
максимум или минимум выше или ниже координаты $y$ в точке
представляет интерес. Конечно, слишком много точек «рядом» с точкой
чтобы проверить, но небольшое размышление показывает, что нам нужно проверить только два, если мы
известно, что $f$ непрерывна (напомним, что это означает, что график
В $f$ нет ни скачков, ни пробелов).

Предположим, например, что мы определили три точки, в которых
$f’$ равно нулю или не существует: $ds (x_1,y_1)$, $ds (x_2,y_2)$, $ds (x_3,y_3)$,
и $ds x_15. 1.3). Предположим, что мы вычисляем значение $f(a)$ для $ds x_1f(x_2)$? Нет: если бы они были, график шел бы вверх от
$(a,f(a))$ до $(b,f(b))$, затем вниз до $ds (x_2,f(x_2))$ и где-то в
между ними будет точка локального максимума. (Это не очевидно, это
результат теоремы об экстремальном значении, теорема 6.1.2.)
Но в этом локальном максимуме
производная от $f$ была бы нулевой или не существовала бы, но мы
уже известно, что производная равна нулю или не существует только при $ds x_1$,
$ds ​​x_2$ и $ds x_3$. В результате одно вычисление говорит нам, что
$ds ​​(x_2,f(x_2))$ имеет наибольшую координату $y$ любой точки на
график около $ds x_2$ и левее $ds x_2$. Мы можем выполнить то же самое
тест справа. Если мы обнаружим, что по обе стороны от $ds x_2$ значения
меньше, то должен быть локальный максимум в точке $ds (x_2,f(x_2))$; если
находим, что по обе стороны от $ds x_2$ значения больше, тогда
должен быть локальный минимум в $ds (x_2,f(x_2))$; если мы найдем один из каждого,
то нет ни локального максимума, ни минимума в точке $ds x_2$. 2-1$. Это определяется
везде и равен нулю в $ds x=pm sqrt{3}/3$. Глядя сначала на
$ds ​​x=sqrt{3}/3$, мы видим, что $ds f(sqrt{3}/3)=-2sqrt{3}/9$. Теперь мы тестируем
две точки по обе стороны
$ds ​​x=sqrt{3}/3$, убедившись, что ни один из них не находится дальше, чем
ближайшее критическое значение; так как $dssqrt{3}-2sqrt{3}/9$
и $ds f(1)=0>-2sqrt{3}/9$, должен быть локальный минимум при
$ds ​​x=sqrt{3}/3$. Для $ds x=-sqrt{3}/3$ мы видим, что
$ds ​​f(-sqrt{3}/3)=2sqrt{3}/9$. На этот раз мы можем использовать $x=0$ и $x=-1$,
и мы находим, что $ds f(-1)=f(0)=0

Конечно, этот пример сделан очень простым благодаря нашему выбору точек для
тест, а именно $x=-1$, $0$, $1$. Мы могли бы использовать другие значения, например
$-5/4$, $1/3$ и $3/4$, но это сделало бы расчеты
значительно утомительнее.

Пример 5.1.3
Найдите все локальные точки максимума и минимума для
$f(x)=sinx+cosx$. Производная равна $f'(x)=cos x-sin x$. Это
всегда определен и равен нулю всякий раз, когда $cos x=sin x$.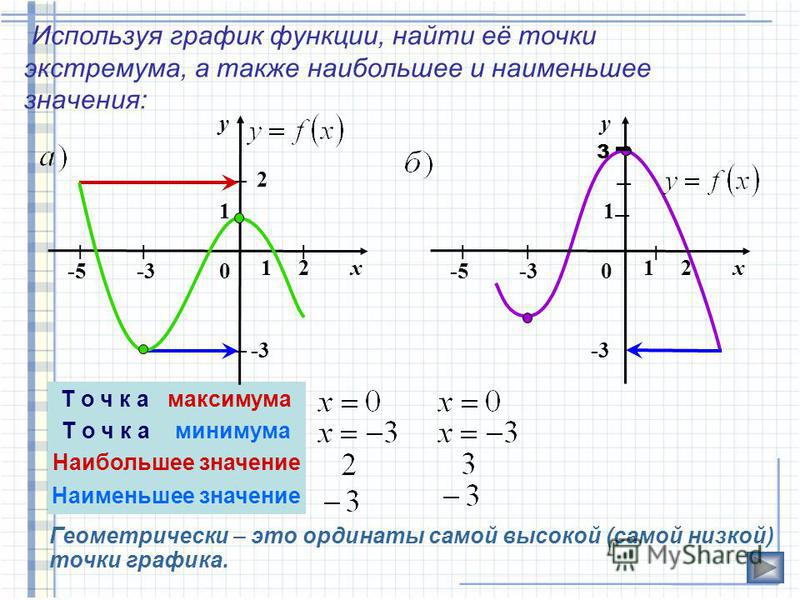 напоминая, что
$cos x$ и $sin x$ — координаты $x$ и $y$ точек на
единичный круг, мы видим, что $cos x=sin x$, когда $x$ равно $pi/4$,
$pi/4pmpi$, $pi/4pm2pi$, $pi/4pm3pi$ и т. д. Поскольку оба синуса
и косинус имеют период $2pi$, нам нужно только определить состояние
$x=pi/4$ и $x=5pi/4$. Мы можем использовать $0$ и $pi/2$ для проверки
критическое значение $x= pi/4$.
Получаем, что $ds f(pi/4)=sqrt{2}$, $ds f(0)=1

Мы используем $pi$ и $2pi$ для проверки критического значения $x=5pi/4$.
соответствующие значения: $ds f(5pi/4)=-sqrt2$, $ds f(pi)=-1>-sqrt2$,
$ds ​​f(2pi)=1>-sqrt2$, поэтому существует локальный минимум при $x=5pi/4$,
$5pi/4pm2pi$, $5pi/4pm4pi$ и т. д. Более кратко:
локальные минимумы при $5pi/4pm 2kpi$ для
каждое целое число $k$.
$квадрат$

В задачах 1–12 найти все локальные максимумы и минимумы
точек $(x,y)$ методом, описанным в этом разделе.

Пример 5.1.1 92 &$x neq 0$cr}$
(отвечать)

Пример 5. 1.13
Для любого действительного числа $x$ существует единственный
целое число $n$ такое, что $n leq x

Пример 5.1.14
Объясните, почему функция $f(x)=1/x$ не имеет локальных
максимумы или минимумы.

Пример 5.1.15
Сколько критических точек может иметь квадратичная полиномиальная функция?
(отвечать)

Пример 5.1.16
Покажите, что кубический многочлен может иметь не более двух критических
точки. Приведите примеры, показывающие, что кубический многочлен может иметь нуль,
одна или две критические точки.
92 + Ьх = (ах + Ь)х.
end{выравнивание}
Следовательно, если $(x,c)$ находится на кривой, то либо $ax + b = 0$, либо $x = 0$.
Установив $x_1 = -dfrac ba$ и $x_2 = 0$, мы можем подставить эти два значения
для $x$ и подтвердите, что действительно две точки
$left(-frac ba, cright)$ и $(0, c)$ лежат на кривой.

Используя предположение, что кривая симметрична относительно вертикальной оси,
вертикальная ось должна быть на полпути между
$left(-frac ba, cright)$ и $(0, c)$, т.

Наибольшее и наименьшее значение функции

Как найти?

Постановка задачи

Найти наибольшее и наименьшее значение функции $ f(x) $ на отрезке $ [a,b] $

План решения

Наибольшее и наименьшее значение непрерывной функции $ f(x) $ на промежутке $ [a,b] $ достигаются в критических точках, то есть в точках в которых производная функции равна нулю $ f'(x) = 0 $, бесконечности $ f'(x) = pm infty $, не существует, либо на концах отрезка $ [a,b] $

1. Проверяем на непрерывность функцию $ f(x) $ на заданном отрезке
2. Если функция непрерывная, то находим производную $ f'(x) $ и приравниваем её к нулю
3. Решая уравнение $ f'(x) = 0 $ получаем корни, являющиеся критическими точками
4. Выбираем критические точки, принадлежащие отрезку $ [a,b] $
5. Вычисляем значения функции $ f(x) $ в оставшихся критических точках, а так же на концах промежутка $ [a,b] $. Затем выбираем из них наибольшее $ M $ и наименьшее $ m $

Примеры решений

Пример 1

Найти наибольшее и наименьшее значение функции $ y = 2x^3 – 3x^2 – 4 $ на отрезке $ [0;2] $

Решение

Функция представляет собой кубический многочлен. Точек разрыва нет, значит функция непрерывна на отрезке $ [0;2] $. Находим производную: $$ y’ = (2x^3 – 3x^2 – 4)’ = 6x^2 – 6x $$ Приравниваем производную к нулю. Решаем уравнение и получаем критические точки: $$ 6x^2 – 6x = 0 $$ $$ 6x(x – 1) = 0 $$ $$ x_1 = 0, x_2 = 1 $$ Проверяем принадлежность полученных точек отрезку $ [0;2] $: $$ x_1 in [0;2], x_2 in [0;2] $$ Так как обе точки принадлежат отрезку, то вычисляем в них значение функции $ f(x) $, так же значение этой функции на концах интервала $ [0;2] $: $$ y(x_1) = y(a) = f(0) = 2 cdot 0^3 – 3 cdot 0^2 – 4 = -4 $$ $$ y(x_2) = y(1) = 2 cdot 1^3 – 3 cdot 1^2 – 4 = -5 $$ $$ y(b) = y(2) = 2 cdot 2^3 – 3 cdot 2^2 – 4 = 0 $$ Среди полученных значений наибольшее $ M = 0 $, наименьшее $ m = -5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ M = 0, m = -5 $$

Пример 2

Найти наименьшее и наибольшее значение функции $ y = frac{4x^2}{3+x^2} $ на $ [-1;1] $

Решение

Функция непрерывна на $ x in [-1;1] $ так как знаменатель не обращается в ноль ни при каком $ x $. Выполняем нахождение производной: $$ y’ = (frac{4x^2}{3+x^2})’ = frac{(4x^2)'(3+x^2)-(4x^2)(3+x^2)’}{(3+x^2)^2} = $$ $$ = frac{8x(3+x^2)-(4x^2)(2x)}{(3+x^2)^2} = frac{24x+8x^3-8x^3}{3+x^2)^2} = frac{24x}{(3+x^2)^2} $$ Приравниваем полученную производную к нулю и вычисляем критические точки: $$ frac{24x}{(3+x^2)^2} = 0 $$ $$ 24x = 0, 3+x^2 neq 0 $$ $$ x = 0 $$ Получена единственная критическая точка $ x = 0 $, которая принадлежит $ [-1; 1] $. Вычисляем значение функции $ f(x) $ в критической точке и на концах интервала $ [-1;1] $: $$ y(-1) = frac{4cdot (-1)^2}{3+(-1)^2} = frac{4}{4}=1 $$ $$ y(0) = frac{0}{3} = 0 $$ $$ y(1) = frac{4cdot 1^2}{3+1^2} = frac{4}{4} = 1 $$ Из полученных значений видно, что максимальное значение $ M = 1 $ и минимальное значение $ m = 0 $.

Ответ

$$ m = 0, M = 1 $$

Математики и Data Science-специалисты должны хорошо разбираться в функциях. Предлагаем попрактиковаться в решении задач на обнаружение максимальных и минимальных значений у заданных функций.

Максимум

Задумываясь над тем, как найти максимальное значение функции, нужно четко понимать, с чем предстоит иметь дело. Для этого нужно запомнить такое определение:

Наибольшее значение функции y = f(x) на промежутке x – это max y = f(x₀). Оно будет при любом значении x€ X, x≠x₀ делает справедливым неравенство: f(x)≤f(x₀).

Максимальное значение (максимум) – это точка на функции, в которой значение функции больше, чем в соседних «отметках».

Минимум

Наименьшее значение функции находить так же легко, как и наибольшее. Но сначала нужно понимать, что это такое.

Значение функции на отрезке будет считаться минимумом, если оно меньше, чем в соседних «отметках». Здесь действует такое определение:

Наименьшее значение функции y=f(x) на промежутке x – это miny=f(x₀), которое при любом значении x€ X, x≠x₀ делает справедливым неравенство f(x)≥f(x₀).

Соответствующие определения являются достаточными и очевидными. Если говорить простыми словами, то максимум функции – это ее самое большое значение на заданном промежутке (участке) при абсциссе x₀, а минимум – самое маленькое.

Стационарные точки

При решении вопроса о том, как найти наибольшее или наименьшее значение функции, стоит обратить внимание на так называемые «стационарные точки». Это – значения аргумента функции, при которых ее производная будет равняться нулю.

Стационарная точка – это «отметка», в которой расположен экстремум дифференцируемой функции. А именно – локальный минимум или максимум. В одной из таких «отметок» записанное выражение будет достигать своих предельных параметров.

Здесь рекомендуется запомнить следующее:

1. Экстремум функции – это минимумы и максимумы.
2. Если определить производную в точках экстремумов, она будет равно 0.
3. Когда говорят «экстремумы», подразумевается значение функции. Если же речь идет об «отметках» экстремумов, рассматривать стоит x, в которых достигаются соответствующие пределы.

 Этого достаточно для того, чтобы разобраться, как найти наибольшее на заданном отрезке у выражения. Для реализации поставленной задачи вовсе не обязательно составлять график. Поэтому сначала воспользуемся записями формул и вычислений.

План действий

Пример – дана функция f(x) на отрезке [a, b]. Наибольшее и наименьшее значение такой непрерывной функции достигаются в определенных местах. Это – критические точки. Там, где производная записанного выражения будет равно нулю.

Для того, чтобы найти наибольшие значения уравнения, потребуется придерживаться следующего алгоритма:

1. Узнайте, какая перед вами функция. Для этого нужно проверить ее на непрерывность. В расчет обязательно берется заданный отрезок.
2. Если запись непрерывная – ищем производную.
3. После того, как найдем производную, приравниваем ее к нулю. Это поможет найти точки экстремумов. В результате получаются корни.
4. Образовавшиеся корни – это критические точки. Нужно выбрать те «параметры», что относятся к промежутку [a, b].
5. Вычислить значения функции на концах отрезка [a, b].
6. Определить значения имеющегося выражения в критических «отметках».

Теперь понятно, как найти наибольшие функции на заданном отрезке. После произведенных подсчетов остается выбрать из результатов M (максимум) и m (минимум).

На отрезке

Разобравшись в тем, как найти наибольшие «параметры» выражения «на бумаге», стоит рассмотреть соответствующий процесс на графиках. Определять максимумы/минимумы в данном случае будет проще.

Первый график указывает на выражение, у которого точка минимума и максимума находятся в стационарных точках на промежутке [-6;6]. Соответствующие «пределы» обозначены жирным.

Второй график указывает на изменение отрезка. Теперь он будет [1;6]. Минимальное значение останется прежним. А вот максимальное – изменится. Оно образуется в правой части в точке с абсциссой. Поиск минимального «параметра» окажется в критической точке.

Задумываясь, как найти наименьшие или «самые крупные» параметры выражения на графике, можно также рассмотреть третий рисунок. Здесь функция принадлежала промежутку [-3;2]. Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы.

Открытый интервал

Если промежуток задан конкретным числом, определить экстремумы будет не так сложно. Иначе происходит, если интервал открыт.

Здесь:

1. Функция будет принимать максимум/минимум по значению в стационарных точках на открытом интервале от -6 до 6. Ответ – на 4 рисунке.
2. Если взять отрезок [1;6), минимум будет достигнут в стационарной точке. А вот максимум – неизвестен. Связано это с тем, что 6 не принадлежит к заданному интервалу. Если бы «шестерка» относилась к соответствующему промежутку, ответ на вопрос относительно определения максимума оказался понятным. Максимальный параметр был бы в точке с абсциссой 6.
3. На рисунке 6, задумываясь, как найти наименьшие «параметры», нужно обратить внимание на заданный интервал. Он равен (-3;2]. Минимум будет достигнут в правой границе. А вот максимум – не определен.

Найти значения на графиках обычно проще, чем «в чистых формулах». Соответствующие задания можно отыскать тут.

Бесконечность

Иногда значения функций нужно найти на бесконечном промежутке. Графически возможны такие ситуации:

На 7 рисунке функция достигает максимума в стационарной точке с абсциссой 1. Минимум окажется на границе интервала справа. На минус бесконечности значения приближаются к y=3 асимптотически.

Если взять интервал от 2-х до «плюс бесконечности», заданная функция не будет иметь ни максимумов, ни минимумов. Значения здесь стремятся к бесконечности. Связано это с тем, что x=2 является вертикальной асимптотой. Если абсцисса стремится к плюс бесконечности, значения будут асимптотически подходить к y=3. Соответствующий пример показан на рисунке 8.

Чтобы не приходилось долго разбираться с тем, как найти наименьшее у заданной функции, не путаться с тем, какие знаки производной использовать, а также легко строить графики, можно воспользоваться специальными онлайн калькуляторами. А еще – закончить тематические дистанционные онлайн курсы.

Исследование функций и их графиков – это тема, которой уделяется особое внимание в рамках школьной программы старших классов. Некоторые основы математического анализа – дифференцирования – включены в профильный уровень экзамена по математике. У некоторых школьников возникают проблемы с этой темой, так как они путают графики функции и производной, а также забывают алгоритмы. В этой статье будут рассмотрены основные типы заданий и способы их решения.

Что такое значение функции?

Вам будет интересно:Проверочное слово к слову «скворец», корень и лексическое значение

Математическая функция представляет собой особое уравнение. Оно устанавливает взаимосвязь между числами. Функция зависит от значения аргумента.

Значение функции рассчитывается по заданной формуле. Для этого следует подставить любой аргумент, который соответствует области допустимых значений, в эту формулу на место х и выполнить необходимые математические операции. Какие?

Как можно найти наименьшее значение функции, используя график функции?

Вам будет интересно:Горизонтальный перенос генов: основы генетики, история открытия, принцип действия и примеры

Графическое изображение зависимости функции от аргумента называется графиком функции. Он строится на плоскости с определенным единичным отрезком, где по горизонтальной оси абсцисс откладывается значение переменной, или аргумента, а по вертикальной оси ординат – соответствующее ему значение функции.

Чем больше значение аргумента, тем правее он лежит на графике. И чем больше значение самой функции, тем выше находится точка.

О чем это говорит? Самым маленьким значением функции будет являться точка, которая лежит ниже всего на графике. Для того чтобы найти его на отрезке графика, нужно:

1) Найти и отметить концы этого отрезка.

2) Визуально определить, какая точка на этом отрезке лежит ниже всего.

3) В ответ записать ее числовое значение, которое можно определить, спроецировав точку на ось ординат.

Точки экстремума на графике производной. Где искать?

Вам будет интересно:Покои – это многозначное слово. Что именно оно означает?

Однако при решении задач иногда дан график не функции, а ее производной. Для того чтобы случайно не допустить глупую ошибку, лучше внимательно читать условия, так как от этого зависит, где нужно искать точки экстремума.

Итак, производная – это мгновенная скорость возрастания функции. Согласно геометрическому определению производная соответствует угловому коэффициенту касательной, которая непосредственно проведена к данной точке.

Известно, что в точках экстремума касательная параллельна оси Ox. Это значит, что ее угловой коэффициент – 0.

Из этого можно сделать вывод, что в точках экстремума производная лежит на оси абсцисс или обращается в ноль. Но кроме того, в этих точках функция меняет свое направление. То есть после периода возрастания начинает убывать, а производная, соответственно, сменяется с положительной на отрицательную. Или наоборот.

Если производная из положительной становится отрицательной – это точка максимума. Если из отрицательной становится положительной – точка минимума.

Важно: если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если требуется найти значение функции, то предварительно нужно подставить соответствующее значение аргумента в функцию и рассчитать его.

Как находить точки экстремума с помощью производной?

Рассмотренные примеры в основном относятся к заданию под номером 7 экзамена, которое подразумевает работу с графиком производной или первообразной. А вот задание 12 ЕГЭ – найти наименьшее значение функции на отрезке (иногда – наибольшее) – выполняется без каких-либо чертежей и требует базовых навыков математического анализа.

Для его выполнения нужно уметь находить точки экстремума с помощью производной. Алгоритм их нахождения таков:

• Найти производную от функции.
• Приравнять ее к нулю.
• Найти корни уравнения.
• Проверить, являются ли полученные точки точками экстремума или перегиба.

Для этого нужно начертить схему и на получившихся промежутках определить знаки производной, подставляя числа, принадлежащие отрезкам, в производную. Если при решении уравнения вы получили корни двойной кратности – это точки перегиба.

• Применив теоремы, определить какие точки являются точками минимума, а какие – максимума.

Вычисление наименьшего значения функции с применением производной

Однако, выполнив все эти действия, мы найдем значения точек минимума и максимума по оси абсцисс. Но как найти наименьшее значение функции на отрезке?

Что необходимо сделать для того, чтобы найти число, которому соответствует функция в конкретной точке? Нужно подставить в данную формулу значение аргумента.

Точки минимума и максимума соответствуют наименьшему и наибольшему значению функции на отрезке. Значит, чтобы найти значение функции, нужно рассчитать функцию, используя полученные значения х.

Важно! Если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если нужно найти значение функции, то предварительно следует подставить соответствующее значение аргумента в функцию и выполнить необходимые математические операции.

Что делать, если на данном отрезке отсутствуют точки минимума?

Но как найти наименьшее значение функции на отрезке, на котором отсутствуют точки экстремума?

Это значит, что на нем функция монотонно убывает или возрастает. Тогда в функцию нужно подставить значение крайних точек этого отрезка. Есть два пути.

1) Рассчитав производную и промежутки, на которых она положительна или отрицательна, сделать вывод о том, убывает функция на данном отрезке или возрастает.

В соответствии с ними подставить в функцию большее или меньшее значение аргумента.

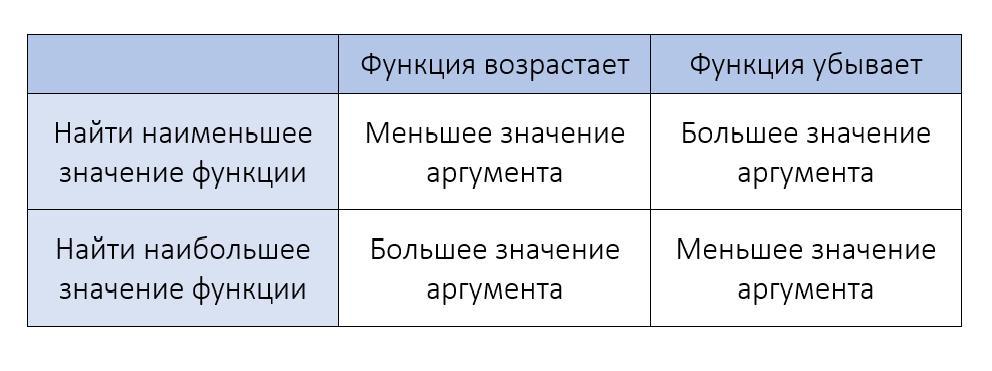
2) Просто подставить в функцию обе точки и сравнить полученные значения функции.

В каких заданиях нахождение производной необязательно

Как правило, в заданиях ЕГЭ все же нужно находить производную. Есть только пара исключений.

1) Парабола.

Вершина параболы находится по формуле.

Если a < 0, то ветви параболы направлены вниз. И ее вершина является точкой максимума.

Если a > 0, то ветви параболы направлены вверх, вершина – точка минимума.

Рассчитав точку вершины параболы, следует подставить ее значение в функцию и вычислить соответствующее значение функции.

2) Функция y = tg x. Или y = ctg x.

Эти функции являются монотонно возрастающими. Поэтому, чем больше значение аргумента, тем больше значение самой функции. Далее мы рассмотрим, как найти наибольшее и наименьшее значение функции на отрезке с примерами.

Основные типы заданий

Задание: наибольшее или наименьшее значение функции. Пример на графике.

На рисунке вы видите график производной функции f (x) на интервале [-6; 6]. В какой точке отрезка [-3; 3] f (x) принимает наименьшее значение?

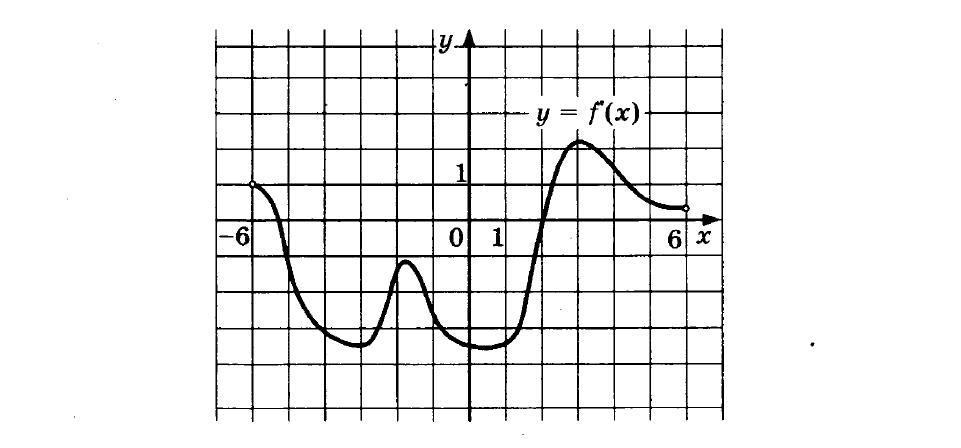
Итак, для начала следует выделить указанный отрезок. На нем функция один раз принимает нулевое значение и меняет свой знак – это точка экстремума. Так как производная из отрицательной становится положительной, значит, это точка минимума функции. Этой точке соответствует значение аргумента 2.

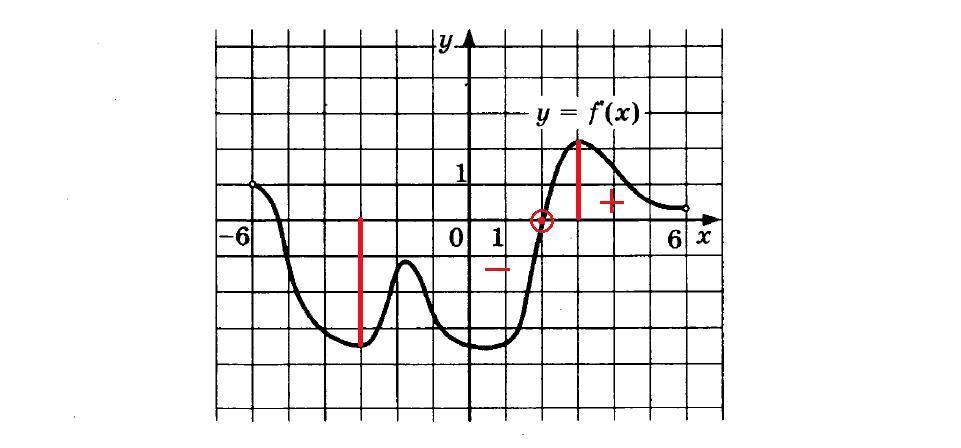
Ответ: 2.

Продолжаем рассматривать примеры. Задание: найти наибольшее и наименьшее значение функции на отрезке.

Найдите наименьшее значение функции y = (x – 8) ex-7 на отрезке [6; 8].

1. Взять производную от сложной функции.

y’ (x) = (x – 8) ex-7 = (x – 8)’ (ex-7) + (x – 8) (ex-7)’ = 1 * (ex-7) + (x – 8) (ex-7) = (1 + x – 8) (ex-7) = (x – 7) (ex-7)

2. Приравнять полученную производную к нулю и решить уравнение.

y’ (x) = 0

(x – 7) (ex-7) = 0

x – 7 = 0, или ex-7 = 0

x = 7; ex-7 ≠ 0, нет корней

3. Подставить в функцию значение крайних точек, а также полученные корни уравнения.

y (6) = (6 – 8) e6-7 = -2e-1

y (7) = (7 – 8) e7-7 = -1 * e0 = -1 * 1 = -1

y (8) = (8 – 8) e8-7 = 0 * e1 = 0

Ответ: -1.

Итак, в этой статье была рассмотрена основная теория о том, как найти наименьшее значение функции на отрезке, необходимая для успешного решения заданий ЕГЭ по профильной математике. Также элементы математического анализа применяются при решении заданий из части С экзамена, но очевидно, они представляют иной уровень сложности, и алгоритмы их решений сложно уместить в рамки одного материала.