Как найти наименьшее значение функции дискриминант

Была ли эта статья полезной?

Если Вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет Вам потом огромную помощь во всей вашей работе

М.И. Калинин 

Одной из главных функций школьной математики, для которой построена полная теория и доказаны все свойства, является квадратичная функция. Учащихся должны четко понимать и знать все эти свойства. При этом задач на квадратичную функцию существует великое множество – от очень простых, которые вытекают непосредственно из теории и формул, до самых сложных, решение которых требует анализа и глубокого понимания всех свойств функции.

При решении задач на квадратичную функцию большое практическое значение имеет наличие соответствия между алгебраическим описание задачи и ее геометрической интерпретацией – изображением на координатной плоскости эскиза графика функции. Именно благодаря этой особенности у вас всегда есть возможность проверить правильность и непротиворечивость своих теоретических рассуждений.

Рассмотрим несколько задач по теме «Квадратичная функция» и остановимся на подробном их решении.   

Задача 1.

Найти сумму целых значений числа p, при которых вершина параболы y = 1/3x² – 2px + 12p расположена выше оси Ox.

Решение.

Ветви параболы направлены вверх (a = 1/3 > 0). Так как вершина параболы лежит выше оси Ox, то парабола не пересекает ось абсцисс (рис. 1).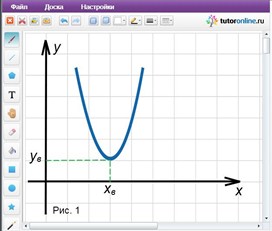 Значит, функция

y = 1/3x² – 2px + 12p не имеет нулей,

а уравнение

1/3x² – 2px + 12p = 0 не имеет корней.

Это возможно, если дискриминант последнего уравнения окажется отрицательным.

Вычислим его:

D/4 = p² – 1/3·12p = p² – 4p;

p² – 4p < 0;

p(p – 4) < 0;

p принадлежит интервалу (0; 4).

Сумма целых значений числа p из промежутка (0; 4): 1 + 2 + 3 = 6.

Ответ: 6.

Заметим, что для ответа на вопрос задачи можно было решить неравенство

y_в > 0 или (4ac – b²) / 4a > 0.

Задача 2.

Найти количество целых значений числа a, при которых абсцисса и ордината вершины параболы y = (x – 9a)² + a² + 7a + 6 отрицательны.

Решение.

Если квадратичная функция имеет вид

y = a(x – n)² + m, то точка с координатами (m; n) является вершиной параболы.

В нашем случае

х_в = 9a; y_в = a² + 7a + 6.

Так как и абсцисса, и ордината вершины параболы должны быть отрицательны, то составим систему неравенств:

{9a < 0,
{a² + 7a + 6 < 0;

Решим полученную систему:

{a < 0,
{(a+ 1)(a + 6) < 0;

Изобразим решение неравенств на координатных прямых и дадим окончательный ответ:

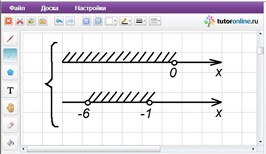
a принадлежит промежутку (-6; -1).

Целые значения числа a: -5; -4; -3; -2. Их количество: 4.

Ответ: 4.

Задача 3.

Найти наибольшее целое значение числа m, при котором квадратичная функция
y = -2x² + 8x + 2m принимает только отрицательные значения.

Решение.

Ветви параболы направлены вниз (a = -2 < 0). Данная  функция будет принимать только отрицательные значения, если ее график не будет иметь общих точек с осью абсцисс, т.е. уравнение -2x² + 8x + 2m = 0 не будет иметь корней. Это возможно, если дискриминант последнего уравнения будет отрицательным.

-2x² + 8x + 2m = 0.

Разделим коэффициенты уравнения на -2, получим:

x² – 4x – m = 0;

D/4 = 2² – 1 · 1 · (-m) = 4 + m;

4 + m < 0;

m < -4.

Наибольшее целое значение числа m: -5.

Ответ: -5.                                                        

Для ответа на вопрос задачи можно было решить неравенство y_в < 0 или

(4ac – b²) / 4a < 0.

Задача 4.

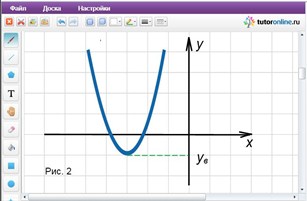
Найти наименьшее значение квадратичной функции y = ax² – (a + 6)x + 9, если известно, что прямая x = 2 является осью симметрии ее графика.

Решение.

1) Так как прямая x = 2 является осью симметрии данного графика, то x_в = 2. Воспользуемся формулой

x_в = -b / 2a, тогда x_в = (a + 6) / 2a. Но x_в = 2.

Составим уравнение:

(a + 6) / 2a = 2;

a + 6 = 4a;

3a = 6;

a = 2.

Тогда функция принимает вид

y = 2x² – (2 + 6)x + 9;

y = 2x² – 8x + 9.

2) Ветви параболы

y = 2x² – 8x + 9 направлены вверх (a = 2 > 0).

Наименьшее значение данной функции равно ординате вершины параболы (рис. 2), которую легко найти, воспользовавшись формулой

y_в = (4ac – b²) / 4a.

y_в = (4 · 2 · 9 – 8²) /4 · 2 = (72 – 64) / 8 = 8/8 = 1.

Наименьшее значение рассматриваемой функции равно 1.

Ответ: 1.

Задача 5.

Найти наименьшее целое значение числа a, при котором множества значений функции  y = x² – 2x + a и y = -x² + 4x – a не пересекаются.

Решение.

Найдем множество значений каждой функции.

I способ.

y₁ = x² – 2x + a.  

Применим формулу

y_в = (4ac – b²) / 4a.

y_в = (4 · 1 · a – 2²) /4 · 1 = (4a – 4) / 4 = 4(a – 1) / 4 = a – 1.

Так как ветви параболы направлены вверх, то

E(y) = [y_в; +∞), т.е. E(y₁) = [a – 1; +∞).

Множество значений функции

y₂ = -x² + 4x – a найдем, выделив полный квадрат в формуле функции.

II способ.

y₂ = -(x² – 4x + a);

y₂ = -(x² – 4x + 4 – 4 + a);

y₂ = -((x – 2)² – 4 + a);

y₂ = -(x – 2)² +  4 – a;

y_в = 4 – a.

Так как ветви параболы направлены вниз, то  

E(y) = (-∞; y_в].

E(y₂) = (-∞; 4 – a].

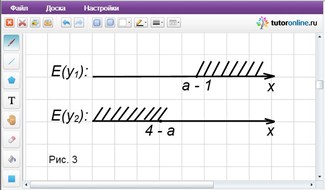
Изобразим полученные множества на координатных прямых (рис. 3).

Полученные множества не будут пересекаться, если точка с координатой 4 – a будет располагаться левее точки с координатой a – 1, т.е.

4 – a < a – 1;

-2a < -5;

a > 2,5.

Наименьшее целое значение числа a: 3.

Ответ: 3.

Задачи на расположение корней квадратичной функции, задачи с параметрами и задачи, сводящиеся к квадратичным функциям, очень популярны на ЕГЭ. Поэтому при подготовке к экзаменам стоит обратить на них пристальное внимание.

 Остались вопросы? Не знаете, как построить график квадратичной функции?
Чтобы получить помощь репетитора – зарегистрируйтесь.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Решение задач на нахождение наибольших и наименьших значений

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Квадратичная функция

Часто квадратичную функцию применяют при решении различных задач, которые сводятся к нахождению тех или иных наибольших или наименьших значений. Но перед рассмотрением таких задач стоит напомнить, какая функция является квадратичной и как найти наибольшее/наименьшее значение.

Определение 1

Функция, имеющая вид $y=ax^2+bx+c$, где $a$ не равняется нулю, называется квадратичной функцией.

График такой функции принято называть параболой. Отметим, что если $a >0$ то ее ветви будут направлены вверх и ее вершина будет принимать минимальное значение, а если $a

Наибольшее и наименьшее значение

Определение 2

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наибольшее значение в точке $x’in X$, если выполняется

[fleft(xright)le f(x’)]

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Бесплатное пробное занятие

*количество мест ограничено

Определение 3

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наименьшее значение в точке $x’in X$, если выполняется

[fleft(xright)ge f(x’)]

Чтобы найти наименьшее и наибольшее значение заданной функции на каком либо отрезке необходимо произвести следующие действия:

1. Найти $f'(x)$;
2. Найти точки, в которых $f’left(xright)=0$;
3. Найти точки, в которых $f'(x)$ не будет существовать;
4. Выкинуть из точек, найденных в пунктах 2 и 3 те, которые не лежат в отрезке $[a,b]$;
5. Вычислить значения в оставшихся точках и на концах $[a,b]$;
6. Выбрать из этих значений наибольшее и наименьшее.

Приведем пример на нахождение наибольшего и наименьшего значения функции.

Пример 1

Найти наибольшее и наименьшее значения на [0,6]:$fleft(xright)=x^3-3x^2-45x+225$

Решение.

1. $f’left(xright)=3x^2-6x-45$;

2. $f’left(xright)=0$;

   [3x^2-6x-45=0] [x^2-2x-15=0] [x=5, x=-3]

3. $f'(x)$ существует на всей $D(f)$;

4. $5in left[0,6right]$;

5. Значения:

   [fleft(0right)=225] [fleft(5right)=50] [fleft(6right)=63]

6. Наибольшее значение равняется $225$, наименьшее равняется $50.$

Ответ: $max=225, min=50$.

«Решение задач на нахождение наибольших и наименьших значений» 👇

Рассмотрим далее задачи на использование наибольшего и наименьшего значений квадратичной функции.

Примеры задач

Пример 2

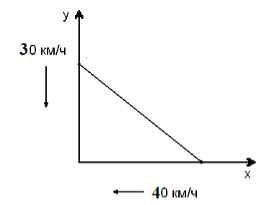
По перекрестным дорогам движутся два автомобиля в сторону перекрестка. Каждому автомобилю до перекрестка ехать по $50$ км. Автомобили движутся со скоростями $30$ и $40$ км/ч, соответственно. Найти, когда автомобили будут друг от друга на наименьшем расстоянии и на каком.

Решение.

Изобразим ситуацию на рисунке (рис. 1).

Рисунок 1.

Пусть наименьшее расстояние между автомобилями будет в момент времени $t$.

В это время одному автомобилю до перекрестка остается ехать

[50-30t км]

А второму

[50-40t км]

Расстояние между ними, по теореме Пифагора, будет равняться

[Sleft(tright)={(50-30t)}^2+{(50-40t)}^2=2500-3000t+{900t}^2+2500-4000t+{1600t}^2={2500t}^2-7000t+5000]

Найдем наименьшее значение такой функции

[t=-frac{b}{2a}=-frac{-7000}{5000}=frac{7}{5}=1,4] [Sleft(tright)=2500cdot frac{49}{25}-7000cdot frac{7}{5}+5000=4900-9800+5000=100]

Ответ: $1$ ч $24$ мин, $100$ км.

Пример 3

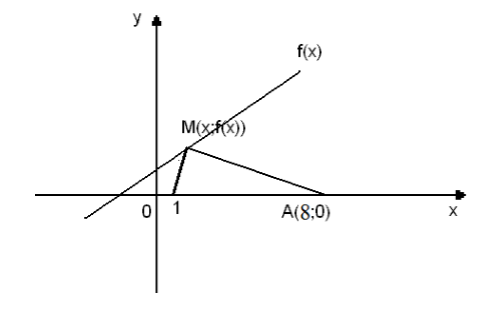
Найти на графике функции $y=x+2$ точку, которая дает наименьшую сумму квадратов расстояний от него до точки $(8,0)$ и $(1,0)$.

Решение.

Рассмотрим рисунок:

Рисунок 2.

Обозначим абсциссу искомой точки через $x$. Точка искомая точка имеет вид $(x,x+1)$.

Найдем расстояние до точки $(8,0)$: $sqrt{{(8-x)}^2+{(x+1)}^2}$

Найдем расстояние до точки $(1,0)$: $sqrt{{(1-x)}^2+{(x+1)}^2}$

Получаем, сумма равна

[Sleft(xright)={(8-x)}^2+{(x+1)}^2+{(1-x)}^2+{(x+1)}^2=64-16x+x^2+1+2x+x^2+1-2x+x^2+1+2x+x^2=4x^2+18x+67]

Наименьшее значение

[x=-frac{18}{8}=-frac{9}{4}=-2,25] [y=frac{81}{4}-frac{162}{4}+frac{268}{4}=frac{187}{4}=46,75]

Ответ: $(-2,25;46,75)$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 13.07.2022

На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно осуществить поиск и определить оптимальное значение какого-либо параметра или количество. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.

Обычно нами строится выражение этих значений в рамках некоторого интервала x, который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [a; b], так и открытый интервал (a; b), (a; b], [a; b), бесконечный интервал (a; b), (a; b], [a; b) либо бесконечный промежуток -∞; a, (-∞; a], [a; +∞), (-∞; +∞).

В этом материале мы расскажем, как найти наибольшее и наименьшее значение явно заданной функции с одной  переменной y=f(x)y=f(x), чтобы вам не нужно было искать это самостоятельно онлайн.

Основные определения

Начнем, как всегда, с формулировки основных определений: какое значение называют максимальным и минимальным?.

Наибольшее значение функции y=f(x) на некотором промежутке x – это значение max y=f(x0)x∈X, которое при любом значении xx∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).

Минимальное значение функции y=f(x) на некотором промежутке x– это значение minx∈Xy=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(Xf(x)≥f(x0).

Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее наибольшее число, которое она может принимать на известном интервале при абсциссе x0, а наименьшее – это самое маленькое принимаемое значение на том же интервале при x0.

Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0.

Зачем нам нужно знать, что такое стационарные точки?  Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или то, что больше всего, значение на некотором промежутке именно в одной из стационарных точек.

Еще  функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.

Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы можем определить наибольшее или найти наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с  границами области определения, или если мы имеем дело с интервалом, не имеющим конца. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения (мало и много). В этих случаях определить или найти наибольшее и/или наименьшее значение не представляется возможным.

Более понятными эти моменты станут после изображения на графиках:

Наибольшее и наименьшее значение функции на отрезке

Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [-6;6].

Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.

На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [-3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.

Наибольшее и наименьшее значение функции на открытом интервале

Теперь посмотрим на четвертый рисунок. В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).

Если мы возьмем интервал [1;6), то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x, равном 6, если бы x=6 принадлежала интервалу. Именно этот случай нарисован на графике 5.

На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (-3;2], а о наибольшем значении мы не можем сделать определенных выводов.

Наибольшее и наименьшее значение функции на бесконечности

На рисунке 7 мы видим, что функция будет иметь max y в стационарной точке, имеющей абсциссу, равную 1. Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y=3.

Если мы возьмем интервал x∈2; +∞, то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2, то значения функции будут стремиться к минус бесконечности, поскольку прямая x=2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.

Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке

Как найти наибольшее и наименьшее значение функции на отрезке?

В этом пункте мы приведем последовательность действий, которую нужно выполнить, чтобы найти наибольшее значение функции на некотором отрезке или как найти наименьшее значение функции.

1. Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
2. Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
3. Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
4. Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x=a и x=b.
5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.

Посмотрим, как правильно применить этот алгоритм при решении задач.

См. на рисунке:

Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале

Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнавать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.

1. Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
2. Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
3. Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0, решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям.  Их определяет вид интервала.

• Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b-0f(x).
• Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+0f(x).
• Если интервал имеет вид  (a;b), то нам надо вычислить односторонние пределы limx→b-0f(x),limx→a+0f(x).
• Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
• Если интервал выглядит как (-∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→-∞f(x).
• Если -∞; b, то считаем односторонний предел limx→b-0f(x) и предел на минус бесконечности limx→-∞f(x)
• Если же -∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x),  limx→-∞f(x).

1. В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4-8 в первой части материала.

Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.

Это все, что мы  хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.

Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.

Наибольшее и наименьшее значение функции

Как найти?

Постановка задачи

Найти наибольшее и наименьшее значение функции $ f(x) $ на отрезке $ [a,b] $

План решения

Наибольшее и наименьшее значение непрерывной функции $ f(x) $ на промежутке $ [a,b] $ достигаются в критических точках, то есть в точках в которых производная функции равна нулю $ f'(x) = 0 $, бесконечности $ f'(x) = pm infty $, не существует, либо на концах отрезка $ [a,b] $

1. Проверяем на непрерывность функцию $ f(x) $ на заданном отрезке
2. Если функция непрерывная, то находим производную $ f'(x) $ и приравниваем её к нулю
3. Решая уравнение $ f'(x) = 0 $ получаем корни, являющиеся критическими точками
4. Выбираем критические точки, принадлежащие отрезку $ [a,b] $
5. Вычисляем значения функции $ f(x) $ в оставшихся критических точках, а так же на концах промежутка $ [a,b] $. Затем выбираем из них наибольшее $ M $ и наименьшее $ m $

Примеры решений

Пример 1

Найти наибольшее и наименьшее значение функции $ y = 2x^3 – 3x^2 – 4 $ на отрезке $ [0;2] $

Решение

Функция представляет собой кубический многочлен. Точек разрыва нет, значит функция непрерывна на отрезке $ [0;2] $. Находим производную: $$ y’ = (2x^3 – 3x^2 – 4)’ = 6x^2 – 6x $$ Приравниваем производную к нулю. Решаем уравнение и получаем критические точки: $$ 6x^2 – 6x = 0 $$ $$ 6x(x – 1) = 0 $$ $$ x_1 = 0, x_2 = 1 $$ Проверяем принадлежность полученных точек отрезку $ [0;2] $: $$ x_1 in [0;2], x_2 in [0;2] $$ Так как обе точки принадлежат отрезку, то вычисляем в них значение функции $ f(x) $, так же значение этой функции на концах интервала $ [0;2] $: $$ y(x_1) = y(a) = f(0) = 2 cdot 0^3 – 3 cdot 0^2 – 4 = -4 $$ $$ y(x_2) = y(1) = 2 cdot 1^3 – 3 cdot 1^2 – 4 = -5 $$ $$ y(b) = y(2) = 2 cdot 2^3 – 3 cdot 2^2 – 4 = 0 $$ Среди полученных значений наибольшее $ M = 0 $, наименьшее $ m = -5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ M = 0, m = -5 $$

Пример 2

Найти наименьшее и наибольшее значение функции $ y = frac{4x^2}{3+x^2} $ на $ [-1;1] $

Решение

Функция непрерывна на $ x in [-1;1] $ так как знаменатель не обращается в ноль ни при каком $ x $. Выполняем нахождение производной: $$ y’ = (frac{4x^2}{3+x^2})’ = frac{(4x^2)'(3+x^2)-(4x^2)(3+x^2)’}{(3+x^2)^2} = $$ $$ = frac{8x(3+x^2)-(4x^2)(2x)}{(3+x^2)^2} = frac{24x+8x^3-8x^3}{3+x^2)^2} = frac{24x}{(3+x^2)^2} $$ Приравниваем полученную производную к нулю и вычисляем критические точки: $$ frac{24x}{(3+x^2)^2} = 0 $$ $$ 24x = 0, 3+x^2 neq 0 $$ $$ x = 0 $$ Получена единственная критическая точка $ x = 0 $, которая принадлежит $ [-1; 1] $. Вычисляем значение функции $ f(x) $ в критической точке и на концах интервала $ [-1;1] $: $$ y(-1) = frac{4cdot (-1)^2}{3+(-1)^2} = frac{4}{4}=1 $$ $$ y(0) = frac{0}{3} = 0 $$ $$ y(1) = frac{4cdot 1^2}{3+1^2} = frac{4}{4} = 1 $$ Из полученных значений видно, что максимальное значение $ M = 1 $ и минимальное значение $ m = 0 $.

Ответ

$$ m = 0, M = 1 $$