Как найти наименьшее значение функции гиперболы - Сайт, где вы сможете решить свои вопросы

Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Функция у = k/x, ее свойства и график

Функция у = k/x, ее свойства и график

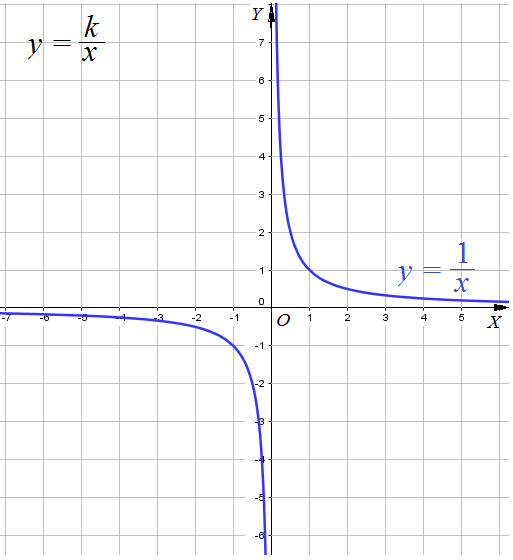
В этом параграфе мы познакомимся с новой функцией — функцией Коэффициент k может принимать любые значения, кроме k = 0. Рассмотрим сначала случай, когда k = 1; таким образом, сначала речь пойдет о функции .

Чтобы построить график функции , поступим так же, как и в предыдущем параграфе: дадим независимой переменной х несколько конкретных значений и вычислим (по формулe ) соответствующие значения зависимой переменной у. Правда, на этот раз удобнее проводить вычисления и построения постепенно, сначала придавая аргументу только положительные значения, а затем — только отрицательные.

Первый этап. Если х = 1, то у = 1 (напомним, что мы пользуемся формулой );

Короче говоря, мы составили следующую таблицу:

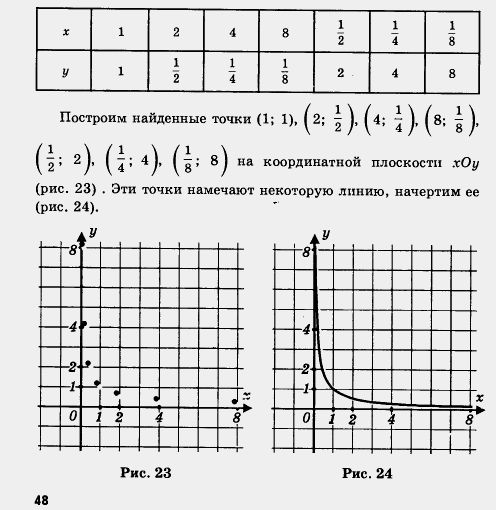
Второй этап.

Короче говоря, мы составили следующую таблицу:

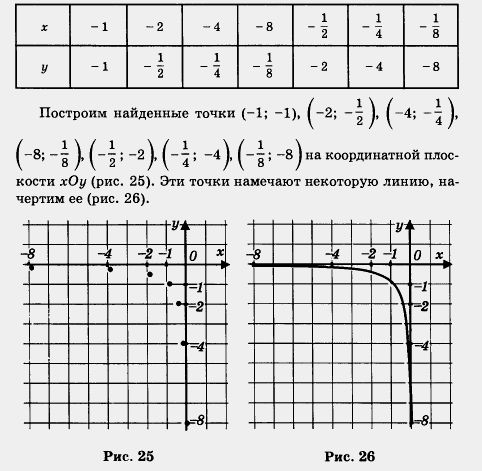
А теперь объединим два этапа в один, т. е. из двух рисунков 24 и 26 сделаем один (рис. 27). Это и есть график функции его называют гиперболой.
Попробуем по чертежу описать геометрические свойства гиперболы.

Во-первых, замечаем, что эта линия выглядит так же красиво, как парабола, поскольку обладает симметрией. Любая прямая, проходящая через начало координат О и расположенная в первом и третьем координатных углах, пересекает гиперболу в двух точках, которые лежат на этой прямой по разные стороны от точки О, но на равных расстояниях от нее (рис. 28). Это присуще, в частности, точкам (1; 1) и (- 1; – 1),

и т. д.Значит – О центр симметрии гиперболы. Говорят также, что гипербола симметрична относительно начала координат.

Во-вторых, видим, что гипербола состоит из двух симметричных относительно начала координат частей; их обычно называют ветвями гиперболы.

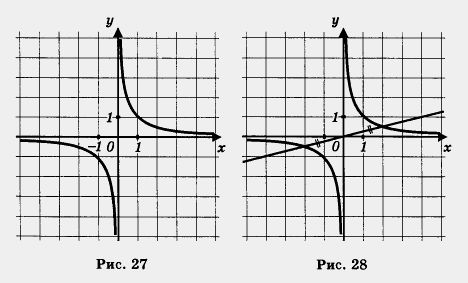
В-третьих, замечаем, что каждая ветвь гиперболы в одном направлении подходит все ближе и ближе к оси абсцисс, а в другом направлении — к оси ординат. В подобных случаях соответствующие прямые называют асимптотами.

Значит, график функции , т.е. гипербола, имеет две асимптоты: ось х и ось у.

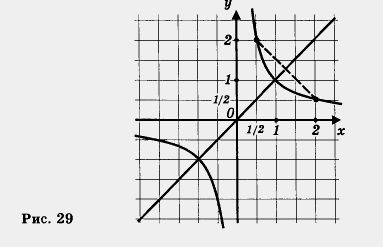
Если внимательно проанализировать построенный график, то можно обнаружить еще одно геометрическое свойство, не такое очевидное, как три предыдущих (математики обычно говорят так: «более тонкое свойство»). У гиперболы имеется не только центр симметрии, но и оси симметрии.

В самом деле, построим прямую у = х (рис. 29). А теперь смотрите: точки расположены по разные стороны от проведенной прямой, но на равных расстояниях от нее. Они симметричны, относительно этой прямой. Тоже можно сказать о точках , где, конечно Значит, прямая y =x – ось симетрии гиперболы ( равно как и y = -x)

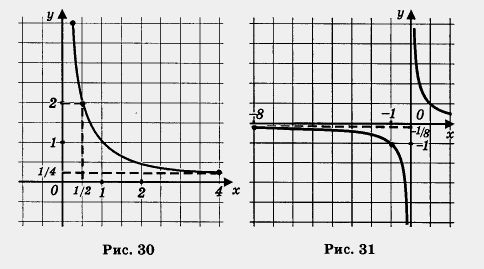
Пример 1. Найти наименьшее и наибольшее значения функции а) на отрезке ; б) на отрезке [- 8, – 1].
Решение, а) Построим график функции и выделим ту его часть, которая соответствует значениям переменной х из отрезка (рис. 30). Для выделенной части графика находим:

б) Построим график функции и выделим ту его часть, которая соответствует значениям переменной х из отрезка [- 8, – 1] (рис. 31). Для выделенной части графика находим:

Итак, мы рассмотрели функцию для случая, когда k= 1. Пусть теперь k — положительное число, отличное от 1, например k = 2.

Рассмотрим функцию и составим таблицу значений этой функции:

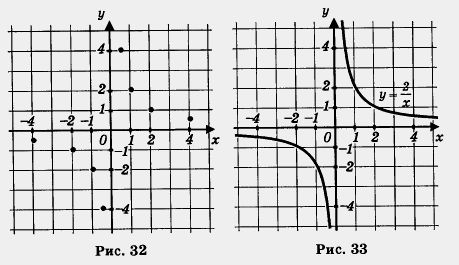
Построим точки (1; 2), (2; 1), (-1; -2), (-2; -1),

на координатной плоскости (рис. 32). Они намечают некоторую линию, состоящую из двух ветвей; проведем ее (рис. 33). Как и график функции , эту линию называют гиперболой.

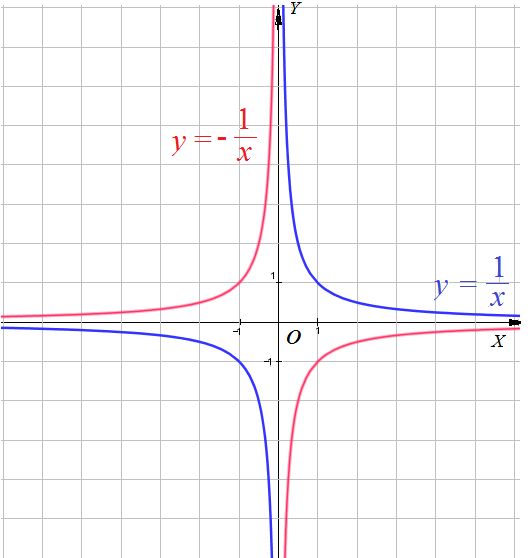
Рассмотрим теперь случай, когда k < 0; пусть, например, k = – 1. Построим график функции (здесь k = – 1).

В предыдущем параграфе мы отметили, что график функции у = -f(x) симметричен графику функции у = f(x) относительно оси х. В частности, это значит, что график функции y = – f(x) симметричен графику функции у = f(x) относительно оси x. В частности, это значит, что график функции , симетричен графику односительно оси абсцисс ( рис. 34) Таким образом, мы получим гиперболу, ветви которой расположены во втором и четвертом координатных углах.

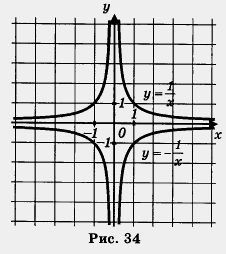
Вообще, графиком функции является гипербола, ветви которой расположены в первом и третьем координатных углах, если k > 0 (рис. 33), и во втором и четвертом координатных углах, если k < О (рис. 34). Точка (0; 0) — центр симметрии гиперболы, оси координат — асимптоты гиперболы.

Обычно говорят, что две величины х и у обратно пропорциональны, если они связаны соотношением ху = k (где k — число, отличное от 0), или, что то же самое, . По этой причине функцию называют иногда обратной пропорциональностью (по аналогии с функцией у – kx, которую, как вы, наверное,
помните, называют прямой пропорциональностью); число k — коэффициент обратной пропорциональности.

Свойства функции при k > 0

Описывая свойства этой функции, мы будем опираться на ее геометрическую модель— гиперболу (см., рис. 33).

1. Область определения функции состоит из всех чисел, кроме х = 0.

2. у > 0 при х>0;у<0 при х<0.

3. Функция убывает на промежутках (-°°, 0) и (0, +°°).

4. Функция не ограничена ни снизу, ни сверху.

5. Ни наименьшего, ни наибольшего значений у функции

6. Функция непрерывна на промежутках (-оо, 0) и (0, +оо) и претерпевает разрыв при х = 0.

Свойства функции при k < 0
Описывая свойства этой функции, мы будем опираться на ее геометрическую модель — гиперболу (см. рис. 34).

1. Область определения функции состоит из всех чисел, кроме х = 0.

2. у > 0 при х < 0; у < 0 при х > 0.

3. Функция возрастает на промежутках (-оо, 0) и (0, +оо).

4. Функция не ограничена ни снизу, ни сверху.

5. Ни наименьшего, ни наибольшего значений у функции нет.

6. Функция непрерывна на промежутках (-оо, 0) и (0, +оо) и претерпевает разрыв при х = 0.

Пример 2. Решить уравнение

Решение.
1) Рассмотрим две функции: и у = 5 – х.
2) Построим график функции гиперболу (рис. 35).
3) Построим график линейной функции Это — прямая, ее можно построить по двум точкам (0; 5) и (5; 0). Она изображена на том же чертеже (рис. 35).

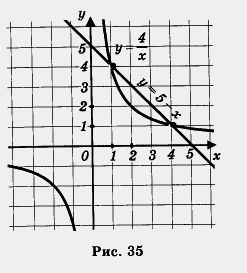
4) По чертежу устанавливаем, что гипербола и прямая пересекаются в точках А (1; 4) и В (4; 1). Проверка показывает, что это на самом деле так.

Значит, данное уравнение имеет два корня: 1 и 4 — это абсциссы точек А и Б.

Ответ: 1,4.

Пример 3. Построить и прочитать график функции у = f(x), где

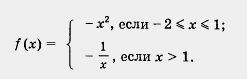
Решение. Построение графика, как обычно в таких случаях, осуществим «по кусочкам». Сначала построим параболу у = – х² и выделим ее часть на отрезке [- 2, 1] (рис. 36).

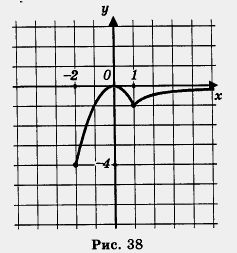
Затем построим гиперболу у и выделим ее часть на открытом луче (1, +оо) (рис. 37). Наконец, оба «кусочка» изобразим в одной системе координат — получим график функции у = f(x) (рис. 38).

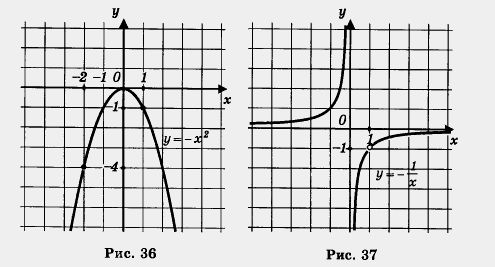
Перечислим свойства функции у = f(x), т.е. прочитаем график.

1. Область определения функции — луч [-2, +оо).

2. у = 0 при х = 0; у < 0 при – 2 < д; < 0 и при я > 0.

3. Функция возрастает на промежутке [-2, 0] и [1, +оо), убывает на отрезке [0, 1].

4. Функция ограничена и снизу и сверху.

5. унаим = – 4 (достигается при х = – 2); _yнаиб = 0 (достигается при х = 0).

6. Функция непрерывна в заданной области определения.

(И В заключение рассмотрим пример, считающийся достаточно сложным.

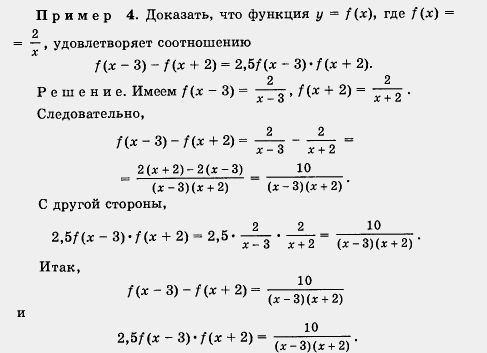
Значит, f(x – 3) – f(x + 2) = 2,5f (х – 3) . f(х + 2), что и требовалось доказать.

Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.

_{Видео по математикескачать, домашнее задание, учителям и школьникам на помощь онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.

Разработка – Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email:

Источник

График дробно-рациональной функции. Гипербола.

Функция $y=frac{k}{x}$ . Гипербола. Свойства.

Пример 1: Построить график для функции $y=frac{1}{x}$, $fleft(xright)=frac{1}{x}$

Вычислим значения функции в разнознаковых точках и нанесем точки с вычисленными координатами в системе $XOY$.
$x=1$ $fleft(1right)=1$ $x=frac{1}{2}$ $fleft(frac{1}{2}right)=2$ $x=-1$ $fleft(-1right)=-1$ $x=-frac{1}{2}$ $fleft(-frac{1}{2}right)=-2$
$x=2$ $fleft(2right)=frac{1}{2}$ $x=frac{1}{4}$ $fleft(frac{1}{4}right)=4$ $x=-2$ $fleft(-2right)=-frac{1}{2}$ $x=-frac{1}{4}$ $fleft(-frac{1}{4}right)=-4$
$x=4$ $fleft(4right)=frac{1}{4}$ $x=frac{1}{8}$ $fleft(1right)=8$ $x=-4$ $fleft(-4right)=-frac{1}{4}$ $x=-frac{1}{8}$ $fleft(-frac{1}{8}right)=-8$ .
В системе координат укажем точки $(1;1)$, $(2;1/2)$, $(4;1/4)$, $(1/2;2)$, $(1/4;4)$, $(1/8;8)$, $(-1;-1)$, $(-2;-1/2)$,
Еще точки: $(-4;-1/4)$, $(-1/2;-2)$, $(-1/4;-4)$, $(-1/8;-8)$ . По всем точкам построим кривые – график функции $y=frac{1}{x}$
Функция $y=frac{1}{x}$ не вычисляется при $x=0$, О.Д.З. $xne0$ . График имеет разрыв по вертикальной линии $x=0$. Ветви “прижаты” к ней.
Ветви графика прижимаются к горизонтальной линии $y=0$. Функция $y=frac{1}{x}$ ни при каких $x$ не принимает значение $y=0$

Графиком функции $y=frac{k}{x}$ $kne0$ является гипербола , ветви прижимаются к асимптотическим линиям.

если коэффициент $k > 0$ , в I и III координатных четвертях. Точка $(0;0)$ – центр симметрии.
если $k < 0$ , то во II и IV координатных четвертях. Точка $(0;0)$ – центр симметрии.
Асимптоты: Вертикальная асимптота, линия $x=0$, Горизонтальная асимптота, линия $y=0$

Cвойства функции $y=frac{k}{x}$ при $k > 0$ ( ветви гиперболы расположены в первом и третьем координатных углах) .

Свойство 1: Область Определения Функции – вся числовая прямая , кроме $x=0$.
Свойство 2: $y > 0$ при $x > 0$; $y < 0$ при $x < 0$.
Свойство 3: Функция убывает на промежутках $( – ∞ ; 0 )$ и $( 0 ; + ∞)$
Свойство 4: Функция не ограничена ни снизу, ни сверху.
Свойство 5: Ни наименьшего, ни наибольшего значений $у$ функций нет.
Свойство 6: Функция непрерывна на $( – ∞ ; 0 )$ и $( 0 ; + ∞)$.
Свойство 7: Область значений функции – $( – ∞ ; 0 )$ U $( 0 ; + ∞)$. имеет разрыв в точке $x=0$.

Cвойства функции $y=frac{k}{x}$ при $k < 0$ (ветви гиперболы расположены во втором и четвертом координатных углах).

Свойство 1: Область Определения Функции – вся числовая прямая , кроме $x=0$.
Свойство 2: $y > 0$ при $x < 0$ ; $y < 0$ при $x > 0$.
Свойство 3: Функция возврастает на промежутках $( – ∞ ; 0 )$ и $( 0 ; + ∞)$
Свойство 4: Функция не ограничена ни снизу, ни сверху.
Свойство 5: Ни наименьшего, ни наибольшего значений $у$ функций нет.
Свойство 6: Функция непрерывна на $( – ∞ ; 0 )$ и $( 0 ; + ∞)$
Свойство 7: Область значений функции – объединение $( – ∞ ; 0 )$ U $( 0 ; + ∞)$ . имеет разрыв в точке $x=0$.

Метод Замены для построения Графика Функции.

Мысль: Умеем строить график функции по-проще … используем его для построения функции при “сдвинутых” аргументах и значениях.

Как построить график функции $y=kcdot fleft(xright)$, если известен график функции $y=fleft(xright)$.

График $y=5cdot fleft(xright)$: Растянуть вертикально вверх по оси $OY$ 5 раз все, что над $OX$ графика $y=fleft(xright)$ , $k$ раза.
График $y=5cdot fleft(xright)$: Расстянуть вертикально вниз по оси $OY$ 5 раз все, что под $OX$ графика $y=fleft(xright)$ , $k$ раза.
График $y=frac{1}{3}cdot fleft(xright)$: Сжать по вертикали, оси $OY$ график $y=fleft(xright)$ 3 раза.
Еще способ: Перемасштабирование. Для $y=5cdot fleft(xright)$ … построить $y=fleft(xright)$, изменить масштаб: “1” станет “5”, “-2” станет “-10”, и т.д.

Как построить график функции $y=-fleft(xright)$, если известен график функции $y=fleft(xright)$.

Эти функции принимают ровно противоположные значения. Значит: график $y=fleft(xright)$ надо отразить по оси $OX$, “перевернуть”.

Как построить график функции $y=fleft(x+lright)$, если известен график функции $y=fleft(xright)$.

Построить график $y=fleft(x+lright)$, где $l > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OX$ на $l$ единиц масштаба влево.
Построить график $y=fleft(x-lright)$, где $l < 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OX$ на $l$ единиц масштаба вправо.

Как построить график функции $y=fleft(xright)+m$, если известен график функции $y=fleft(xright)$.

Построить график $y=fleft(xright)+m$, где $m > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OY$ на $m$ единиц масштаба вверх;
Построить график $y=fleft(xright)-m$, где $m > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OY$ на $m$ единиц масштаба вниз.

Как построить график функции $y=fleft(x+lright)+m$, если известен график функции $y=fleft(xright)$.

График функции $y=fleft(x+lright)+m$ можно получить из графика $y=fleft(xright)$ параллельными сдвигами по осям $OX$ и $OY$.

График Дробной Функции.

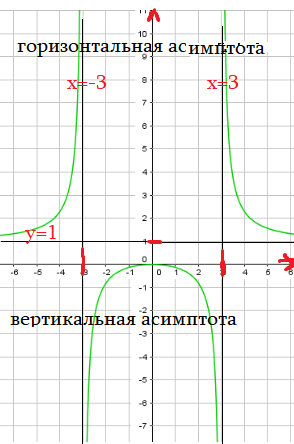
Пример 2: Построить график функции $y=-frac{5}{x+3}$ .

сначала построим график функции $y=-frac{5}{x}$ … от графика $y=frac{1}{x}$ … отразим от $OX$ и растянем по вертикали 5 раз.
сдвинем получившуюся гиперболу вдоль оси $OX$ на $3$ единицы влево, получится требуемый график.
это гипербола с асимптотами $x=-3$; $y=0$. “почему так?” – как мы строим графики?
берем несколько $x$ – точек и находим для каждого свои $y$ – значения в соответствии “с формулой функции”.
По точкам проводим график. Очевидно, если, скажем, $x=0,52$ функция $y=-frac{5}{x+3}$ дает какое-то значение,
… то, конечно для $x=3,52$ другая функция, $y=-frac{5}{x}$ дает ровно такое же значение.
значит, точки графиков будут различаться на $3$ единицы по $x$ – координате и совпадать по $y$ – координате.
Ровно так и для всех точек. “Сравни две функции и вообрази их графики: каковы различия и что общего?”

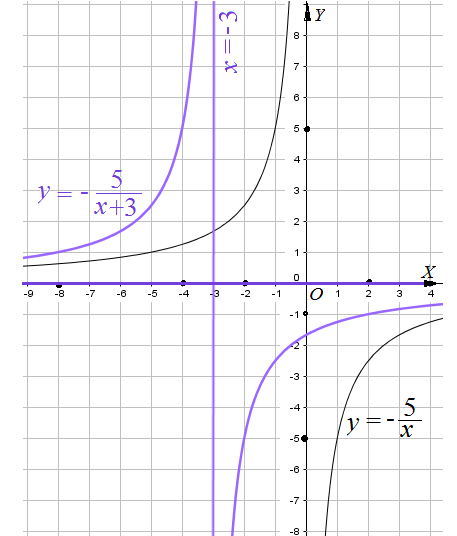
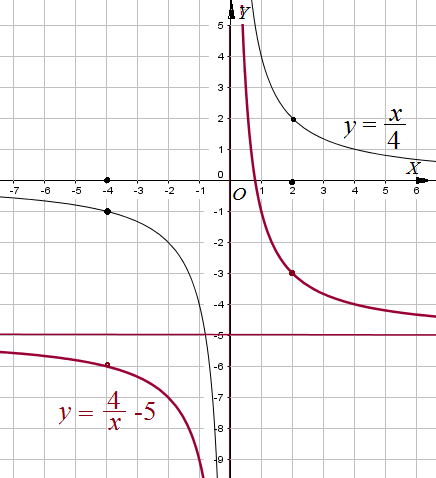
Пример 3: Построить график функции $y=frac{4}{x}-5$ .

Сначала надо построить график функции $y=frac{4}{x}$ . Гиперболу $y=frac{1}{x}$ “растянем” четыре раза.
Сдвинуть получившуюся гиперболу вдоль оси $OY$ на $5$ клеточек вниз. Т.к. каждое значение должно отличаться на 5 единиц.
получится требуемый график. Это гипербола с асимптотами $x=0$; $y=-5$.
Важно знать где пересекается с нулем. Решение, корень $frac{4}{x}-5=0$ дает абсциссу $x=0.8$. Точка графика $left(0,8;0right)$.

Вертикальная асимптота – $x=0$, проходит в полюсе, точке разрыва функции. Точка обнуления знаменателя. Параллельно $OY$.

Горизонтальная асисмптота -$y=-5$, линия, на которую “ложится” график при значениях $х$ около $+-infty$. Параллельно $OX$.

Гипербола – график простой дроби, две асимптоты делят на 4 четверти, ветви гиперболы “зажаты – прижаты” к асимптотическим линиям .

Наклонная асимптота – линия типа $y=2x+3$, к которой “прижимаются” ветви графика “на” или “около” + – бесконечнoсти.

Пример 4: Построить график функции $y=frac{x-5}{x^2-25}$

Если выражение функции упрощается, то следует это сделать. Ибо получится функция проще, легче вычисляемая и рисуемая.
Тождественное преобразование, сокращение $frac{x-5}{x^2-25}=frac{x-5}{(x+5)(x-5)}=frac{1}{x+5}$. Так, что график $y=frac{1}{x+5}$ ?
Не спеши! Мы сократили на $x-5$ , которое незаконно для $x=5$. Нарушается О.Д.З – в исходной функции нет места $x=5$.
Значит: можем строить гиперболу $y=frac{1}{x+5}$ взамен нашей $y=frac{x-5}{x^2-25}$, но “без точки $x=5$”.
Точка $x=5$ разрывает “гладкий” график гиперболы. Она называется “выколотая точка с координатами $left(5;0,1right)$”.

Важно уметь исследовать функцию – график около точек разрыва. + / – поблизости. Куда тянется?

Исследуем около $x=-5$. Возьмем “близкие” точки $-5,01$ и $-4,99$. Вычислим приближенные значения.
Чуть левее … $fleft(-5,01right)=frac{-5,01-5}{(-5,01)^2-5^2}approx -100$. Чуть правее … $fleft(-4,99right)=frac{-4,99-5}{(-4,99)^2-5^2}approx 100$.
Прямая $x=-5$ – вертикальная асимптота. Ветвь слева прижимается “вниз”, к $-infty$ . А справа поднимается вверх к $+infty$.
Около $x=5$. Чуть левее $fleft(4,99right)=frac{4,99-5}{4,99^2-5^2}approx0,101$. $fleft(5,01right)=frac{5,01-5}{5,01^2-5^2}approx0,099$.
Значит, $x=5$ точка разрыва, на графике выколотая точка $left(5;0,1right)$. Т.к. в ней $y=frac{1}{5+5}=0,1$.
“О нулях”: при $x=0$ $y=0,2$ . Но функция нигде не обнуляется, $yne0$. Прямая $y=0$ – горизонтальная асимптота.

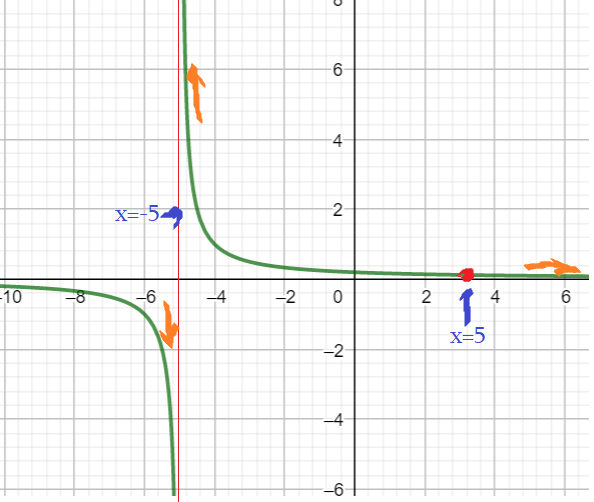
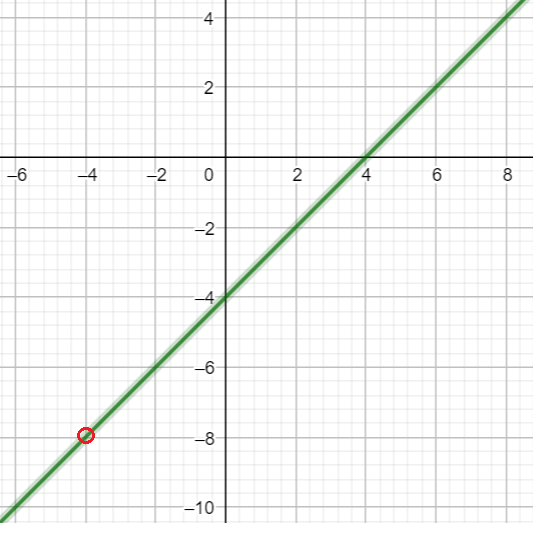
Пример 5: Построить график функции $y=frac{x^2-16}{x+4}$

О.Д.З функции $xne-4$. Оговорив это, со спокойной совестью сократим $y=frac{x^2-16}{x+4}=x-4$.
График нащей функции – прямая линия $y=x-4$ с выколотой точкой $left(-4;-8right)$ при $x=-4$.
“Близко чуть левее”: $x=-4,01$ значение $fleft(-4,01right)=frac{(-4,01)^2-16}{-4,01+4}=-8,01$. Ближе? … Предел $approx-8$.
“О нулях”. при $x=0$ $y=-4$ . Обнуление функции $y=0$ при $x=4$ – пересечение с $x$ – осью.

График Дробно – Рациональной Функции.

Определение: дробно-рациональной порядка $left(n;mright)$ называется функция вида $y=frac{acdot x^n+5x^3-x+c}{bcdot x^m-4x^2-7x+d}$

Числитель – многочлен степени $n$ , знаменатель – многочлен степени $m$ . Общий вид: $y=frac{Pleft(xright)}{Qleft(xright)}$

Нули функции – корни числителя $Pleft(xright)=0$ , Асимптоты (полюсы) – корни знаменателя $Qleft(xright)=0$.

Пример 6: Построить график функции $y=frac{x^2}{x^2-9}$.

Функция $fleft(xright)=frac{x^2}{x^2-9}$ – четная: $fleft(xright)=fleft(xright)$ $fleft(8right)=fleft(-8right)$ – Слева и справа от $OY$ симметрично.
Вычисления: $fleft(-4right)=frac{left(-4right)^2}{left(-4right)^2-9}=frac{16}{7}approx2,3$ $fleft(-10right)=frac{100}{91}approx 1,1$ $fleft(-5right)=frac{25}{16}approx 1,6$ $fleft(-3,5right)=frac{12.25}{3,25}approx 3,8$
$fleft(-2right)=fleft(2right)=frac{4}{-5}approx -0,8$ $fleft(-1right)=fleft(1right)approx -0,1$ $fleft(3,5right)approx 3,8$ $fleft(4right)approx 2,3$ $fleft(5right)approx 1,6$ $fleft(10right)approx 1,1$
Наша функция имеет нули в точке $x=0$ , а вертикальные асимтоты – линии $x=-3$ , $x=3$
Асимптота – прямая линия, к которой “прижимается” график функции, “подходя” к ней бесконечно близко.
Чему равно $frac{x^2}{x^2-9}$ при очень больших $x$ ? $xapproxpm1000$ ? Конечно, $yapprox1$ горизонтальная асимптота $y=1$ .
Анализ графика: 1) Обнуляется при $x=0$ . 2) Значение в нуле : $y=frac{x^2}{x^2-9}$ в $x=0$ равно $y=0$.
3) Поведение в разрывах: “чуть левее” полюса $xapprox-3-0,01$ значение $y > 0$ – “большое положительное”.
“чуть правее” разрыва $xapprox-3+0,01$ значение функции “большое отрицательное”.
Поведение около другого разрыва: когда $x$ “чуть левее” , например $xapprox3-0,01$ , то $y < 0$ ;
когда $x$ “чуть правее” , например $xapprox3+0,01$ , то $y > 0$.
4) Поведение на бесконечности: при $xapproxpminfty$ значение “ложится” около $yapprox1$.
5) Область определения функции – все точки оси $x$ , кроме $x=pm3$
6) Функция положительна $y > 0$ на интервалах $x < -3$ , $x > 3$.
7) Функция отрицательна $y < 0$ на интервалах $-3 < x < 0$ , $0 < x < 3$.

пробaп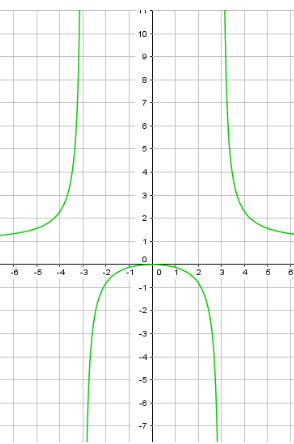

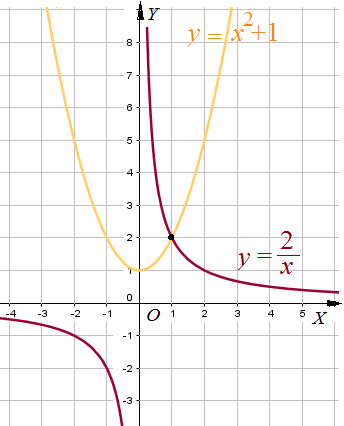
Графический способ решения уравнений

Пример 7: Решить уравнение $frac{2}{x}=x^2+1$ графическим способом.

Рассмотрим две функции : $y=frac{2}{x}$ и $y=x^2+1$ построим гиперболу $y=frac{2}{x}$ и параболу $y=x^2+1$ по
чертежу видно, что графики пересекаются в точке с координатами $left(1;2right)$. если подставить $x=1$ в уравнение,
то равенство выполняется: $frac{2}{1}=1^2+1$ обе функции принимают одно и то же значение $2=2$.
ответ: $x=1$. при таком $x$ графики пересекаются.
“почему?”: при каких $x$ – числах выравниваются обе части уравнения? при тех $x$ – числах, при которых левая
функция и правая функция приобретают одинаковые значения … это то же самое, что графики этих функций
пересекаются в точках с такими $x$ – координатами.

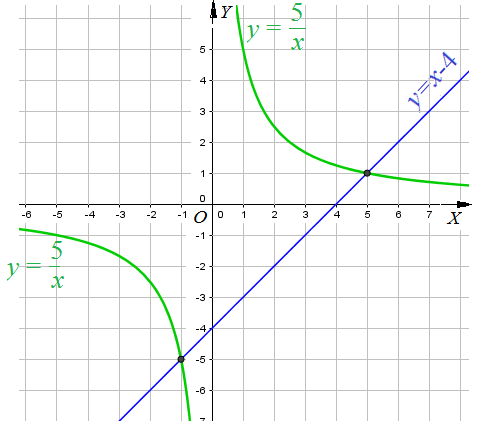
Пример 8: Решить уравнение $frac{5}{x}=x-4$.

рассмотрим две функции: $y=frac{5}{x}$ и $y=x-4$, построим их графики: гиперболу $y=frac{5}{x}$ и прямую $y=x-4$.
по чертежу видно, что гипербола и прямая пересекаются в точках $(-1;-5)$ и $(5;1)$. проверим, подставим
$x=-1$ и $x=5$ в уравнение : $frac{5}{-1}=-1-4$ $Leftrightarrow$ $-5=-5$ и $frac{5}{5}=5-4$ $Leftrightarrow$ $1=1$ . равенство
выполняется, значит данное уравнение имеет два корня – абсциссы точек пересечения графиков.
ответ: $x_1=-1$; $x_2=5$.

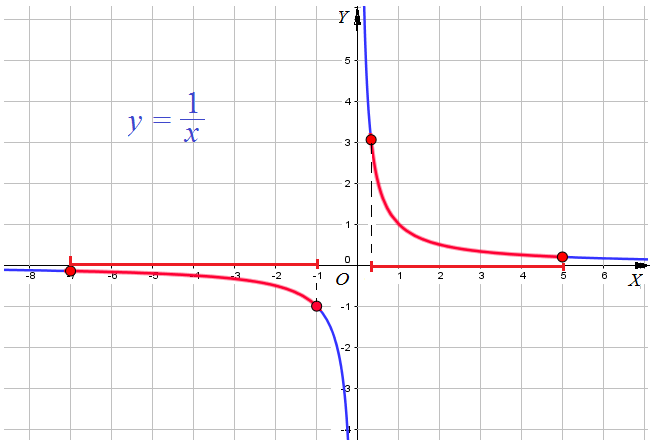
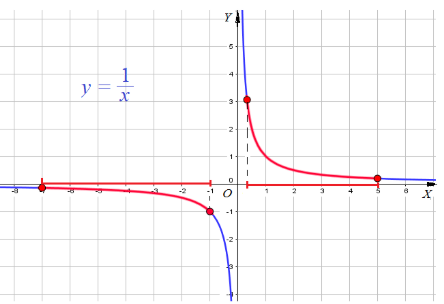
Пример 9: Найти наименьшее и наибольшее значения функции $y=frac{1}{x}$ на отрезках а) $left[frac{1}{3};5right]$ и б) $left[-7;-1right]$.

Построим график функции $y=frac{1}{x}$ .
Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $left[frac{1}{3};5right]$.
Для выделенной части графика находим: наименьшее значение $y=frac{1}{5}$ при $x=5$ , наибольшее $y=3$ при $x=frac{1}{3}$.
Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $left[-7;-1right]$.
Для выделенной части графика находим: наименьшее значение $y=-frac{1}{7}$ при $x=-7$ наибольшее $y=-1$ при $x=-1$.

Пример 10: Доказать, что функция $y=fleft(xright)$ , где $fleft(xright)=frac{4}{x}$

удовлетворяет соотношению $fleft(x-5right)-fleft(x+1right)=1,5cdot fleft(x-5right)cdot fleft(x+1right)$.

Подставим в аргументы функций значения $x-5$ и $x+1$, получим: $fleft(x-5right)=frac{4}{x-5}$ и $fleft(x+1right)=frac{4}{x+1}$ .
распишем левую часть тождества $fleft(x-5right)-fleft(x+1right)=frac{4}{x-5}-frac{4}{x+1}=frac{4left(x+1right)-4left(x-5right)}{left(x-5right)left(x+1right)}=frac{24}{left(x-5right)left(x+1right)}$. аналогично,
с правой стороны получим $1,5cdot fleft(x-5right)cdot fleft(x+1right)=1,5frac{4}{x-5}cdotfrac{4}{x+1}=frac{1,5cdot16}{left(x-5right)left(x+1right)}=frac{24}{left(x-5right)left(x+1right)}$. одинаковые! ч.т.д.

Упражнения

Источник

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Декартова система координат

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

Функция

Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.

Прямая

Линейная функция – функция вида y = a x + b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :

Если a > 0 , прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y .

Если a < 0 , прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .

Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Парабола

Графиком функции y = a x 2 + b x + c является парабола.

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :

Коэффициент a указывает на то, куда направлены ветки параболы.

Если a > 0 , ветки параболы направлены вверх.
Если a < 0 , ветки параболы направлены вниз.

Коэффициент c указывает, в какой точке парабола пересекает ось y.
Коэффициент b помогает найти x в – координату вершины параболы.

x в = − b 2 a

Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .

Если D > 0 – две точки пересечения.
Если D = 0 – одна точка пересечения.
Если D < 0 – нет точек пересечения.

Гипербола

Графиком функции y = k x является гипербола.

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

Если k < 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .

Квадратный корень

Функция y = x имеет следующий график:

Возрастающие/убывающие функции

Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.

Скачать домашнее задание к уроку 5.

Источник

Свойства гиперболы

1) Область определения и область значений

По аналитическому заданию функции видно, что х ≠-a, поскольку знаменатель дроби не может ровняться нулю. Таким образом получим:

D(f)=(-∞;-а) U (-a;+∞)

Область значений

Е(f)=(-∞;+∞)

2) Нули функции

Если b=0, то график функции не пересекает ось ОХ;

Если b≠0, то гипербола имеет одну точку пересечения с ОХ:*

x=-(k+ab)/b

3) Промежутки знакопостоянства

Рассмотрим только 2 простых случая, остальные случаи вы можете рассмотреть аналитически самостоятельно по алгоритму из раздела Свойства функций -> Знакопостоянство

Случай 1: a=0, b=0, k>0

f(x)>0, при x ∈ (0; +∞)

f(x)<0, при x ∈ (-∞;0)

Случай 1: a=0, b=0, k<0

f(x)<0, при x ∈ (0; +∞)

f(x)>0, при x ∈ (-∞;0)

4) Промежутки монотонности

Аналогично с промежутками знакопостоянства рассмотрим только 2 случая

Случай 1: a=0, b=0, k>0

Функция убывает при

x ∈ (-∞;0) U (0; +∞)

Функция возрастает при

x ∈ (-∞;0) U (0; +∞)

5) Четность и нечетность

Функция является нечетной при a=0, b=0, то есть если имеет вид y=k/x

Источник

График функции - гипербола. Готовимся к ОГЭ по математике. Модуль 1. Урок 39

График функции, заданной формулой вида $displaystyle y=frac{k}{x}$ или $displaystyle y=frac{k}{x-m}+n$ , displaystyle kneq 0 , — гипербола.
Область определения функции, заданной формулой $displaystyle y=frac{k}{x}$ , — все действительные числа, кроме 0, значит, график этой функции не пересекает ось ординат. Аналогично график, заданный $displaystyle y=frac{k}{x-m}+n$ , не будет проходить ни через одну точку плоскости с абсциссой (то есть не пересекает вертикальную прямую x=m ).
В зависимости от значений, которые принимают параметры , гипербола $displaystyle y=frac{k}{x}$ – может быть по-разному расположена на декартовой плоскости. При

Рис.1

При наличии параметров и график гиперболы получается из графика $displaystyle y=frac{k}{x}$ параллельным переносом вправо вдоль оси на и вверх вдоль оси на (см. рис. 2).

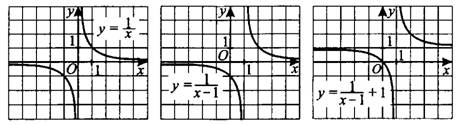
Рис.2

Пример 1. Установите соответствие между графиками функций (см. рис. 3) и формулами, которые их задают.

Рис. 3

1) $displaystyle y=-frac{2}{x}$ ; 2) $displaystyle y=frac{2}{x+1}$ ; 3 ) $displaystyle y=frac{1}{x}$ ; 4) $displaystyle y=-frac{1}{x}$ .
Решение. Все три графика — гиперболы, то есть заданы формулами вида $displaystyle y=frac{k}{x}$ или $displaystyle y=frac{k}{x-m}+n$ .
Для графика А значение параметра k<0 , значит, он может быть задан формулами 1 или 4. Проверим точку (1; -2), через которую проходит этот график. Формула номер 1: $displaystyle y(1)=-frac{2}{1}=-2$ — подходит. Формула номер 4: $displaystyle y(1)=-frac{1}{1}=-1neq -2$ — не подходит. Следовательно, из предложенных формул графику А соответствует формула 1. Для графика Б выполняется

Источник

График дробно-рациональной функции. Гипербола.

Упражнения

Декартова система координат

Функция

Прямая

Парабола

Гипербола

Квадратный корень

Возрастающие/убывающие функции

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.

Вам также может понравиться

Континент ап ошибка 628 как исправить

Как найти массу льда в физике

Как составить должностную инструкцию для работников предприятия

Добавить комментарий Отменить ответ