- Развертка ординаты движения точки по числовой окружности в функцию от угла
- Свойства функции y=sinx
- Примеры
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).
Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.
В результате получаем график y=sinx для любого (xinmathbb{R}).
График y=sinx называют синусоидой.
Часть синусоиды для 0≤x≤2π называют волной синусоиды.
Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды.
п.2. Свойства функции y=sinx
1. Область определения (xinmathbb{R}) – множество действительных чисел.
2. Функция ограничена сверху и снизу
$$ -1leq sinxleq 1 $$
Область значений (yin[-1;1])
3. Функция нечётная
$$ sin(-x)=-sinx $$
4. Функция периодическая с периодом 2π
$$ sin(x+2pi k)=sinx $$
5. Максимальные значения (y_{max}=1) достигаются в точках
$$ x=fracpi2+2pi k $$
Минимальные значения (y_{min}=-1) достигаются в точках
$$ x=-fracpi2+2pi k $$
Нули функции (y_{0}=sinx_0=0) достигаются в точках (x_0=pi k)
6. Функция возрастает на отрезках
$$ -fracpi2+2pi kleq xleqfracpi2+2pi k $$
Функция убывает на отрезках
$$ fracpi2+2pi kleq xleqfrac{3pi}{2}+2pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=sinx на отрезке:
a) (left[fracpi6; frac{3pi}{4}right]) $$ y_{min}=sinleft(fracpi6right)=frac12, y_{max}=sinleft(fracpi2right)=1 $$ б) (left[frac{5pi}{6}; frac{5pi}{3}right]) $$ y_{min}=sinleft(frac{3pi}{2}right)=-1, y_{max}=sinleft(frac{5pi}{6}right)=frac12 $$
Пример 2. Решите уравнение графически:
a) (sinx=3x)
Один корень: x = 0
б) (sinx=2x-2pi)
Один корень: x = π
в) (sinx-sqrt{x-pi}=0)
(sinx=sqrt{x-pi}) 
Один корень: x = π
г*) (sinx=left(x-fracpi2right)^2-frac{pi^2}{4})
(y=left(x-fracpi2right)^2-frac{pi^2}{4}) – парабола ветками вверх, с осью симметрии (x_0=fracpi2) и вершиной (left(fracpi2; -frac{pi^2}{4}right)) (см. §29 справочника для 8 класса)
Два корня: (x_1=0, x_2=pi)
Пример 3. Постройте в одной системе координат графики функций $$ y=sinx, y=-sinx, y=2sinx, y=sinx+2 $$ 
(y=-sinx) – отражение исходной функции (y=sinx) относительно оси OX. Область значений (yin[-1;1]).
(y=2sinx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=sinx+2) – исходная функция поднимается вверх на 2. Область значений (yin[1;3]).
Пример 4. Постройте в одной системе координат графики функций $$ y=sinx, y=sin2x, y=sinfrac{x}{2} $$ 
Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под синусом изменяет период колебаний.
(y=sin2x) – период уменьшается в 2 раза, полная волна укладывается в отрезок (0leq xleq pi).
(y=sinfrac{x}{2}) – период увеличивается в 2 раза, полная волна укладывается в отрезок (0leq xleq 4pi).
Тригонометрические функции
Основная сложность тригонометрических функций состоит в том, что при решении уравнений возникает бесконечное множество корней. Например, уравнение имеет корни Ну и как отмечать их на координатной прямой, если таких чисел бесконечно много?
Ответ прост: надо подставлять конкретные значения n . Ведь в задачах B15 с тригонометрическими функциями всегда есть ограничение — Поэтому для начала берем а затем до тех пор, пока соответствующий корень не «вылезет» за пределы Аналогично, очень скоро получим корень, который меньше нижней границы.
Несложно показать, что никаких корней, кроме полученных в рассмотренном процессе, не существует. Рассмотрим теперь этот процесс на конкретных примерах.
Задача. Найдите точку максимума функции, принадлежащую
y = sin x − 5 x sin x − 5cos x + 1
y ’ = (sin x − 5 x sin x − 5cos x + 1)’ = . =
Затем решаем уравнение:
y ’ = 0;
(1 − 5 x ) cos x = 0;
.
x 1 = 0,2;
x 2 = π /2 + πn , n ∈ Z .
С корнем все понятно, а вот формула требует дополнительной обработки. Будем подставлять разные
Но π /2 > π /3, поэтому корень не входит в исходный отрезок. Кроме того, поэтому нет смысла рассматривать
Но − π /2 < − π /3 — этот корень тоже придется отбросить. А вместе с ним — и все корни
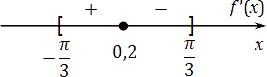
Получается, что на отрезке лежит только корень Отметим его вместе со знаками и границами на координатной прямой:
Чтобы удостовериться, что справа производная действительно отрицательная, достаточно подставить в производную значение Мы же просто отметим, производная меняет знак с плюса на минус, а следовательно, это точка максимума.
Задача. Найдите наибольшее значение функции на отрезке
y = 4 tg x − 4 x + π − 5
y ’ = (4tg x − 4 x + π − 5)’ =
Затем решаем уравнение:
y ’ = 0 ⇒ 4/cos 2 x − 4 = 0 ⇒ . ⇒
Снова выделим из этой формулы корни, подставляя
n = 0 ⇒ x = 0. Этот корень нам подходит.
n = 1 ⇒ x = π . поэтому надо вычеркнуть.
n = −1 ⇒ x = − π . тоже вычеркиваем.
Из всего многообразия корней остался лишь один: Поэтому вычисляем значение функции для Имеем:
y (0) = 4tg 0 − 4 · 0 + π − 5 = π − 5;
y ( π /4) = 4tg π /4 − 4 · π /4 + π − 5 = 1;
y (− π /4) = 4tg (− π /4) − 4 · (− π /4) + π − 5 = . =
Теперь заметим, Получается одно положительное число и два отрицательных. Мы ищем наибольшее — очевидно,
Заметим, что в последней задаче можно было и не сравнивать числа между собой. Ведь из чисел в бланк ответов можно записать лишь единицу.
Действительно, как написать в бланке, скажем, А никак. Это важная особенность первой части ЕГЭ по математике, которая значительно упрощает решение многих задач. И работает она не только в B15.
Случай пустого множества решений
Иногда при исследовании функции возникают уравнения, у которых нет корней. В таком случае задача становится еще проще, поскольку остается рассмотреть лишь концы отрезка.
Однако будьте предельно внимательны, поскольку такие задачи встречаются в ЕГЭ крайне редко. Если в процессе решения выясняется, что корней нет, лучше еще раз проверить все выкладки. И только когда убедитесь, что ошибок нет, можно расслабиться: вам досталась легкая задача!
Задача. Найдите наименьшее значение функции
y = 7sin x − 8 x + 5
Сначала находим производную:
y ’ = (7sin x − 8 x + 5)’ =
Попробуем решить уравнение:
y ’ = 0 ⇒ 7cos x − 8 =
Но значения cos x всегда лежат Поэтому корней нет.
Если корней нет, то и вычеркивать ничего не надо. Переходим к последнему шагу — вычисляем значение функции:
y (−3 π /2) = 7sin (−3 π /2) − 8 · (−3 π /2) + 5 = . =
y(0) = 7sin 0 − 8 · 0 + 5 = 5.
Поскольку число 1 в бланк ответов не записать, остается лишь


 , часть 1
, часть 1 


Наибольшее и наименьшее значения функции на отрезке
Наибольшее и наименьшее значения функции на множестве
(основные определения)
Пусть X – некоторое множество, входящее в область определения D ( f ) функции y = f (x) .
Определение 1. Значение f (x0) функции y = f (x) в точкеназывают наибольшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство
Наибольшее значение функции f (x) на множестве X часто обозначают
Определение 2. Значение f (x0) функции y = f (x) в точке называют наименьшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство
Наименьшее значение функции f (x) на множестве X часто обозначают
Определение 3. Наибольшее значение функции на множестве X часто называют максимальным значением функции f (x) на множестве X или максимумом функции f (x) на множестве X . Наименьшее значение функции на множестве X часто называют минимальным значением функции f (x) на множестве X или минимумом функции f (x) на множестве X .
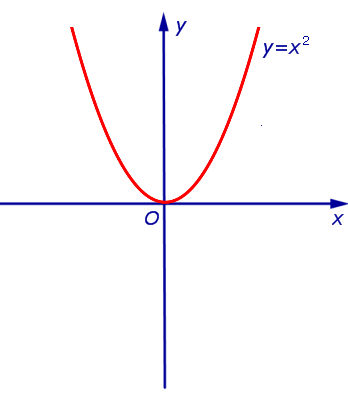
Пример 1. Минимальным значением функции y = x 2 на множестве является число 0 (рис. 1).
Максимального значения функция y = x 2 на множестве не имеет.
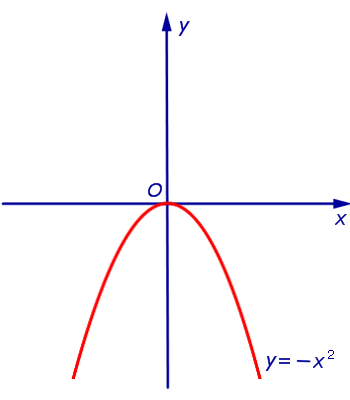
Пример 2. Максимальным значением функции y = – x 2 на множестве является число 0 (рис. 2).
Минимального значения функция y = – x 2 на множестве не имеет.
Пример 3. Функция y = x на множестве не имеет ни максимального, ни минимального значений (рис. 3).
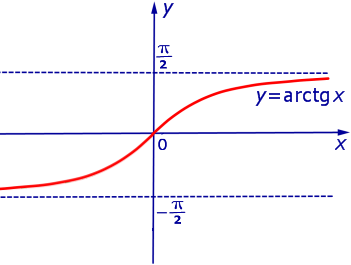
Пример 4. Функция y = arctg x на множестве не имеет ни максимального, ни минимального значений (рис. 4).
Существование наибольшего и наименьшего значений функции на отрезке. Теорема Вейерштрасса
Как мы видели в примерах 1 — 4, даже такие хорошо известные функции, как
не имеют наибольших или наименьших значений на множестве. Однако, если бы в качестве множества X мы взяли произвольный отрезок, то ситуация стала бы принципиально иной, что вытекает из следующей теоремы.
Теорема Вейерштрасса. Если функция непрерывна на отрезке, то на этом отрезке существует точка, в которой функция принимает наибольшее значение, а также точка, в которой функция принимает наименьшее значение.
Доказательство теоремы Вейерштрасса выходит за рамки школьного курса математики и здесь не приводится.
Примеры решения задач
| y = 2x 3 + 3x 2 – 36x + 30 | (1) |
Из формулы (2) получаем, что критическими точками функции (1) являются точки x = – 3 , x = 2, причем только точка x = 2 принадлежит отрезку [–2, 4] . Вычисляя значения функции (1) в критической точке x = 2, а также на концах отрезка x = – 2 и x = 4 , получим:
| y (2) = – 14 , |
| y (– 2) = 98 , |
| y (4) = 62 . |
Ответ. Наибольшее значение функции (1) на отрезке [–2, 4] равно 98 , а наменьшее значение функции (1) на отрезке [–2, 4] равно – 14 .
на отрезке [–1, 27] .
Решая уравнение y’ = 0 , получим
Заметим также, что производная (4) функции (3) не существует в точке x = 0 . Следовательно, у функции (3) есть три критические точки: x = 0, и , причем все эти точки лежат на отрезке [–1, 27] . Вычисляя значения функции (3) в критических точках x = 0, и , а также на концах отрезка x = – 1 и x = 27 , получим:
| y (0) = 0 , |
| y (– 1) = – 1 , |
| y (27) = 99 . |
Ответ. Наибольшее значение функции (3) на отрезке [–1, 27] равно 99 , а наменьшее значение функции (3) на отрезке [–1, 27] равно – 1 .
Решение. Для того, чтобы найти критические точки функции (5), перепишем правую часть формулы (5), используя определение модуля:
В точке x = 0 производная функции (5) не существует. Критическими точками являются точки
Все критические точки принадлежат отрезку [–1, 6] . Вычисляя значения функции (5) в критических точках x = 0, x = 3, x = 5, а также на концах отрезка x = – 1 и x = 6 , получим:
| y (0) = – 4 , |
| y (3) = – e 3 , |
| y (5) = e 5 , |
| y (– 1) = – 5e , |
| y (6) = 2e 6 . |
Ответ. Наибольшее значение функции (5) на отрезке [–1, 6] равно 2e 6 , а наменьшее значение функции (5) на отрезке [–1, 6] равно – e 3 .
| y = (x – 27) e 28 – x | (6) |
на отрезке [23, 40] .
Решая уравнение y’ = 0 , получаем, что функция (6) имеет единственную критическую точку x = 28 , причем эта точка лежит на отрезке [23, 40] . При переходе через точку x = 28 производная функции (7) меняет знак с «+» на «–» , откуда вытекает, что точка x = 28 является точкой максимума функции (6) на множестве . Следовательно, точка x = 28 является точкой максимума функции (6) и на отрезке [23, 40] . Найдем значение функции (6) в точке x = 28 :
Задание 11 Профильного ЕГЭ по математике
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.
В точке производная меняет знак с «минуса» на «плюс». Значит, — точка минимума функции
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция монотонно возрастает, точка максимума функции .будет при том же , что и точка максимума функции А ее найти легко.
при . В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции .
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.
В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции . Поскольку при функция убывает, В этой задаче значение функции на концах отрезка искать не нужно.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
Найдем знаки производной.
Точка — точка минимума функции . Точка не лежит на отрезке Поэтому
и Значит, наименьшее значение функции на отрезке достигается при Найдем это значение.
7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если то Если , то
Значит, — точка минимума функции . В этой точке и достигается наименьшее значение функции на отрезке
8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
Найдем знаки производной на отрезке
При знак производной меняется с «плюса» на «минус». Значит, — точка максимума функции
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции
При знак производной меняется с «минуса» на «плюс». Значит, — точка минимума функции
10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
По условию, . На этом отрезке условие выполняется только для Найдем знаки производной слева и справа от точки
В точке производная функции меняет знак с «плюса» на «минус». Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. — нет решений.
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку , получим, что для всех , и функция монотонно возрастает при
Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при
Тригонометрические функции
6 августа 2012
Основная сложность тригонометрических функций состоит в том, что при решении уравнений возникает бесконечное множество корней. Например, уравнение sin x = 0 имеет корни x = πn, n ∈ Z. Ну и как отмечать их на координатной прямой, если таких чисел бесконечно много?
Ответ прост: надо подставлять конкретные значения n. Ведь в задачах B15 с тригонометрическими функциями всегда есть ограничение — отрезок [a; b]. Поэтому для начала берем n = 0, а затем увеличиваем n до тех пор, пока соответствующий корень не «вылезет» за пределы отрезка [a; b]. Аналогично, уменьшая n, очень скоро получим корень, который меньше нижней границы.
Несложно показать, что никаких корней, кроме полученных в рассмотренном процессе, на отрезке [a; b] не существует. Рассмотрим теперь этот процесс на конкретных примерах.
Задача. Найдите точку максимума функции, принадлежащую отрезку [−π/3; π/3]:
y = sin x − 5x sin x − 5cos x + 1
Вычисляем производную:
y’ = (sin x − 5x sin x − 5cos x + 1)’ = … = cos x − 5x cos x = (1 − 5x) cos x
Затем решаем уравнение:
y’ = 0;
(1 − 5x) cos x = 0;
…
x1 = 0,2;
x2 = π/2 + πn, n ∈ Z.
С корнем x = 0,2 все понятно, а вот формула x = π/2 + πn требует дополнительной обработки. Будем подставлять разные значения n, начиная с n = 0.
n = 0 ⇒ x = π/2
Но π/2 > π/3, поэтому корень x = π/2 не входит в исходный отрезок. Кроме того, чем больше n, тем больше x, поэтому нет смысла рассматривать n > 0.
n = −1 ⇒ x = − π/2
Но −π/2 < −π/3 — этот корень тоже придется отбросить. А вместе с ним — и все корни для n < −1.
Получается, что на отрезке [−π/3; π/3] лежит только корень x = 0,2. Отметим его вместе со знаками и границами на координатной прямой:
Чтобы удостовериться, что справа от x = 0,2 производная действительно отрицательная, достаточно подставить в производную значение x = π/4. Мы же просто отметим, что в точке x = 0,2 производная меняет знак с плюса на минус, а следовательно, это точка максимума.
Задача. Найдите наибольшее значение функции на отрезке [−π/4; π/4]:
y = 4 tg x − 4x + π − 5
Вычисляем производную:
y’ = (4tg x − 4x + π − 5)’ = 4/cos 2x − 4.
Затем решаем уравнение:
y’ = 0 ⇒ 4/cos 2x − 4 = 0 ⇒ … ⇒ x = πn, n ∈ Z.
Снова выделим из этой формулы корни, подставляя конкретные n, начиная с n = 0:
n = 0 ⇒ x = 0. Этот корень нам подходит.
n = 1 ⇒ x = π. Но π > π/4, поэтому корень x = π и значения n > 1 надо вычеркнуть.
n = −1 ⇒ x = −π. Но −π < −π/4, поэтому x = −π и n < −1 тоже вычеркиваем.
Из всего многообразия корней остался лишь один: x = 0. Поэтому вычисляем значение функции для x = 0, x = π/4 и x = −π/4. Имеем:
y(0) = 4tg 0 − 4 · 0 + π − 5 = π − 5;
y(π/4) = 4tg π/4 − 4 · π/4 + π − 5 = 1;
y(−π/4) = 4tg (−π/4) − 4 · (−π/4) + π − 5 = … = 2π − 9.
Теперь заметим, что π = 3,14… < 4, поэтому π − 5 < 4 − 5 < 0 и 2π − 9 < 8 − 9 < 0. Получается одно положительное число и два отрицательных. Мы ищем наибольшее — очевидно, это y = 1.
Заметим, что в последней задаче можно было и не сравнивать числа между собой. Ведь из чисел π − 5, 1 и 2π − 9 в бланк ответов можно записать лишь единицу.
Действительно, как написать в бланке, скажем, число π? А никак. Это важная особенность первой части ЕГЭ по математике, которая значительно упрощает решение многих задач. И работает она не только в B15.
Случай пустого множества решений
Иногда при исследовании функции возникают уравнения, у которых нет корней. В таком случае задача становится еще проще, поскольку остается рассмотреть лишь концы отрезка.
Однако будьте предельно внимательны, поскольку такие задачи встречаются в ЕГЭ крайне редко. Если в процессе решения выясняется, что корней нет, лучше еще раз проверить все выкладки. И только когда убедитесь, что ошибок нет, можно расслабиться: вам досталась легкая задача!
Задача. Найдите наименьшее значение функции на отрезке [−3π/2; 0]:
y = 7sin x − 8x + 5
Сначала находим производную:
y’ = (7sin x − 8x + 5)’ = 7cos x − 8
Попробуем решить уравнение:
y’ = 0 ⇒ 7cos x − 8 = 0 ⇒ cos x = 8/7
Но значения cos x всегда лежат на отрезке [−1; 1], а 8/7 > 1. Поэтому корней нет.
Если корней нет, то и вычеркивать ничего не надо. Переходим к последнему шагу — вычисляем значение функции:
y(−3π/2) = 7sin (−3π/2) − 8 · (−3π/2) + 5 = … = 12π + 12;
y(0) = 7sin 0 − 8 · 0 + 5 = 5.
Поскольку число 12π + 12 в бланк ответов не записать, остается лишь y = 5.
Смотрите также:
- Задача B15: Линейные выражения под знаком тригонометрической функции
- Сложные задачи B15: комбинация тригонометрии и многочленов
- Тест к уроку «Что такое числовая дробь» (средний)
- Метод коэффициентов, часть 1
- Задача B5: вычисление площади методом обводки
- Углы и отрезки в стереометрии — 2
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Исследование тригонометрических функций
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 11 № 26692
i
Найдите наибольшее значение функции на отрезке
Аналоги к заданию № 26692: 3401 70043 517179 … Все
Источник: Пробный ЕГЭ по математике Санкт-Петербург 2015. Вариант 2
Решение
·
Видеокурс
·
Помощь
2
Тип 11 № 26693
i
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26693: 70087 3417 3419 … Все
Решение
·
Видеокурс
·
Помощь
3
Тип 11 № 26694
i
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26694: 3437 70133 70137 … Все
Решение
·
Видеокурс
·
Помощь
4
Тип 11 № 26695
i
Найдите наибольшее значение функции на отрезке
Аналоги к заданию № 26695: 3457 70187 509500 … Все
Источник: Пробный ЕГЭ по профильной математике Санкт-Петербург 05.04.2016. Вариант 2
Решение
·
Видеокурс
·
Помощь
5
Тип 11 № 26696
i
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26696: 3475 70237 3477 … Все
Решение
·
Видеокурс
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5