Как найти наименьшее значение графика производной функции

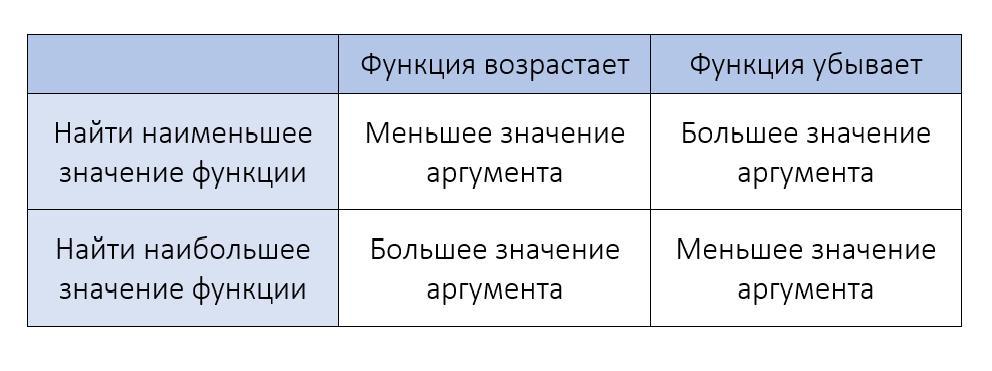
Рассмотрим примеры, в которых дан график производной и требуется определить, в какой точке данного отрезка функция принимает наименьшее значение.

№1

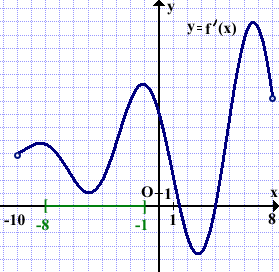
На рисунке изображён график производной функции f(x), определённой на интервале (-10;8). В какой точке отрезка [-8;-1] функция f(x) принимает наименьшее значение?

Решение:

Выделяем отрезок [-8;-1].

На этом отрезке производная f'(x) принимает положительные значения.

Значит, на [-8;-1] функция f(x) возрастает, то есть бо́льшему значению аргумента соответствует бо́льшее значение функции:

x₁,x₂ ∈[-8;-1], x₂>x₁, ⇒ f(x₂)>f(x₁).

Следовательно, наименьшее значение f(x) принимает при наименьшем значении аргумента, то есть на левом конце отрезка, при x=-8.

Ответ: -8.

№2

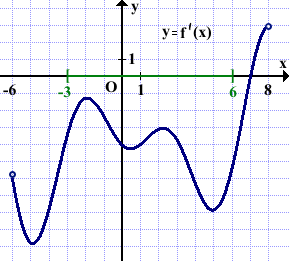
На рисунке изображён график производной функции f(x), определённой на интервале (-6;8). В какой точке отрезка [-3;6] функция f(x) принимает наименьшее значение?

Решение:

Выделяем отрезок [-3;6].

На этом отрезке f'(x)<0, поэтому f(x) убывает, то есть бо́льшему значению аргумента соответствует меньшее значение функции:

x₁,x₂ ∈[-3;6], x₂>x₁, ⇒ f(x₂)<f(x₁).

Поэтому наименьшее значение функция f(x) в этом случае принимает при наибольшем значении аргумента, то есть на правом конце отрезка, при x=6.

Ответ: 6.

№3

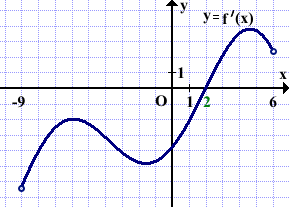
Функция y=f(x) определена на промежутке (-9;6). На рисунке изображён график её производной. Найти абсциссу точки, в которой функция y=f(x) принимает наименьшее значение.

Решение:

В точке с абсциссой x=2 производная меняет знак с минуса на плюс.

Значит, x=2 — точка минимума.

Производная f'(x) существует на всём интервале (-9;6), следовательно, функция f(x) на (-9;6) непрерывна.

Если непрерывная функция f(x) имеет на заданном интервале (a;b) только одну точку экстремума x_o и это точка минимума, то на (a;b) функция принимает своё наименьшее значение в точке x_o.

Таким образом, наименьшее значение функция f(x) принимает в точке с абсциссой x=2.

Ответ: 2.

№4

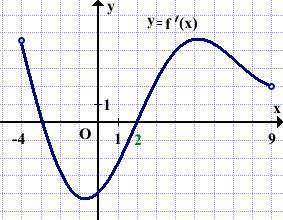
Функция y=f(x) определена и непрерывна на отрезке [-4;9]. На рисунке изображён график её производной. Найти точку x_o, в которой функция принимает наименьшее значение, если f(9)≤f(-4).

Решение:

На промежутках (-4;-3) и (2;9) производная f'(x) принимает положительные значения, поэтому функция f(x) на этих промежутках возрастает.

На промежутке (-3;2) производная f'(x)<0, поэтому функция f(x) убывает.

Так как функция определена и непрерывна на отрезке [-4;9], то точки -4, -3, 2 и 9 можно включить в промежутки монотонности.

Следовательно, функция f(x) возрастает на промежутках [-4;-3] и [2;9] и убывает на [-3;2].

На промежутках возрастания своё наименьшее значение функция принимает на левом конце отрезка. На отрезке [2;9] наименьшее значение f(x) принимает в точке x=2 (точке минимума), на [-4;-3] — в точке x=-4.

Так как на [2;9] функция f(x) возрастает, то f(2)<f(9).

По условию, f(9)≤f(-4). Значит, f(2)<f(-4).

Таким образом, наименьшее значение функция f(x) принимает в точке x=2.

Ответ: 2.

Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).

Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.

Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.

Ответ: (11.)

Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.

Инфоурок

›

Алгебра

›Презентации›Нахождение наибольшего и наименьшего значения производной по графику функции

Нахождение наибольшего и наименьшего значения производной по графику функции

Исследование функций и их графиков – это тема, которой уделяется особое внимание в рамках школьной программы старших классов. Некоторые основы математического анализа – дифференцирования – включены в профильный уровень экзамена по математике. У некоторых школьников возникают проблемы с этой темой, так как они путают графики функции и производной, а также забывают алгоритмы. В этой статье будут рассмотрены основные типы заданий и способы их решения.

Что такое значение функции?

Вам будет интересно:Проверочное слово к слову «скворец», корень и лексическое значение

Математическая функция представляет собой особое уравнение. Оно устанавливает взаимосвязь между числами. Функция зависит от значения аргумента.

Значение функции рассчитывается по заданной формуле. Для этого следует подставить любой аргумент, который соответствует области допустимых значений, в эту формулу на место х и выполнить необходимые математические операции. Какие?

Как можно найти наименьшее значение функции, используя график функции?

Вам будет интересно:Горизонтальный перенос генов: основы генетики, история открытия, принцип действия и примеры

Графическое изображение зависимости функции от аргумента называется графиком функции. Он строится на плоскости с определенным единичным отрезком, где по горизонтальной оси абсцисс откладывается значение переменной, или аргумента, а по вертикальной оси ординат – соответствующее ему значение функции.

Чем больше значение аргумента, тем правее он лежит на графике. И чем больше значение самой функции, тем выше находится точка.

О чем это говорит? Самым маленьким значением функции будет являться точка, которая лежит ниже всего на графике. Для того чтобы найти его на отрезке графика, нужно:

1) Найти и отметить концы этого отрезка.

2) Визуально определить, какая точка на этом отрезке лежит ниже всего.

3) В ответ записать ее числовое значение, которое можно определить, спроецировав точку на ось ординат.

Точки экстремума на графике производной. Где искать?

Вам будет интересно:Покои – это многозначное слово. Что именно оно означает?

Однако при решении задач иногда дан график не функции, а ее производной. Для того чтобы случайно не допустить глупую ошибку, лучше внимательно читать условия, так как от этого зависит, где нужно искать точки экстремума.

Итак, производная – это мгновенная скорость возрастания функции. Согласно геометрическому определению производная соответствует угловому коэффициенту касательной, которая непосредственно проведена к данной точке.

Известно, что в точках экстремума касательная параллельна оси Ox. Это значит, что ее угловой коэффициент – 0.

Из этого можно сделать вывод, что в точках экстремума производная лежит на оси абсцисс или обращается в ноль. Но кроме того, в этих точках функция меняет свое направление. То есть после периода возрастания начинает убывать, а производная, соответственно, сменяется с положительной на отрицательную. Или наоборот.

Если производная из положительной становится отрицательной – это точка максимума. Если из отрицательной становится положительной – точка минимума.

Важно: если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если требуется найти значение функции, то предварительно нужно подставить соответствующее значение аргумента в функцию и рассчитать его.

Как находить точки экстремума с помощью производной?

Рассмотренные примеры в основном относятся к заданию под номером 7 экзамена, которое подразумевает работу с графиком производной или первообразной. А вот задание 12 ЕГЭ – найти наименьшее значение функции на отрезке (иногда – наибольшее) – выполняется без каких-либо чертежей и требует базовых навыков математического анализа.

Для его выполнения нужно уметь находить точки экстремума с помощью производной. Алгоритм их нахождения таков:

• Найти производную от функции.
• Приравнять ее к нулю.
• Найти корни уравнения.
• Проверить, являются ли полученные точки точками экстремума или перегиба.

Для этого нужно начертить схему и на получившихся промежутках определить знаки производной, подставляя числа, принадлежащие отрезкам, в производную. Если при решении уравнения вы получили корни двойной кратности – это точки перегиба.

• Применив теоремы, определить какие точки являются точками минимума, а какие – максимума.

Вычисление наименьшего значения функции с применением производной

Однако, выполнив все эти действия, мы найдем значения точек минимума и максимума по оси абсцисс. Но как найти наименьшее значение функции на отрезке?

Что необходимо сделать для того, чтобы найти число, которому соответствует функция в конкретной точке? Нужно подставить в данную формулу значение аргумента.

Точки минимума и максимума соответствуют наименьшему и наибольшему значению функции на отрезке. Значит, чтобы найти значение функции, нужно рассчитать функцию, используя полученные значения х.

Важно! Если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если нужно найти значение функции, то предварительно следует подставить соответствующее значение аргумента в функцию и выполнить необходимые математические операции.

Что делать, если на данном отрезке отсутствуют точки минимума?

Но как найти наименьшее значение функции на отрезке, на котором отсутствуют точки экстремума?

Это значит, что на нем функция монотонно убывает или возрастает. Тогда в функцию нужно подставить значение крайних точек этого отрезка. Есть два пути.

1) Рассчитав производную и промежутки, на которых она положительна или отрицательна, сделать вывод о том, убывает функция на данном отрезке или возрастает.

В соответствии с ними подставить в функцию большее или меньшее значение аргумента.

2) Просто подставить в функцию обе точки и сравнить полученные значения функции.

В каких заданиях нахождение производной необязательно

Как правило, в заданиях ЕГЭ все же нужно находить производную. Есть только пара исключений.

1) Парабола.

Вершина параболы находится по формуле.

Если a < 0, то ветви параболы направлены вниз. И ее вершина является точкой максимума.

Если a > 0, то ветви параболы направлены вверх, вершина – точка минимума.

Рассчитав точку вершины параболы, следует подставить ее значение в функцию и вычислить соответствующее значение функции.

2) Функция y = tg x. Или y = ctg x.

Эти функции являются монотонно возрастающими. Поэтому, чем больше значение аргумента, тем больше значение самой функции. Далее мы рассмотрим, как найти наибольшее и наименьшее значение функции на отрезке с примерами.

Основные типы заданий

Задание: наибольшее или наименьшее значение функции. Пример на графике.

На рисунке вы видите график производной функции f (x) на интервале [-6; 6]. В какой точке отрезка [-3; 3] f (x) принимает наименьшее значение?

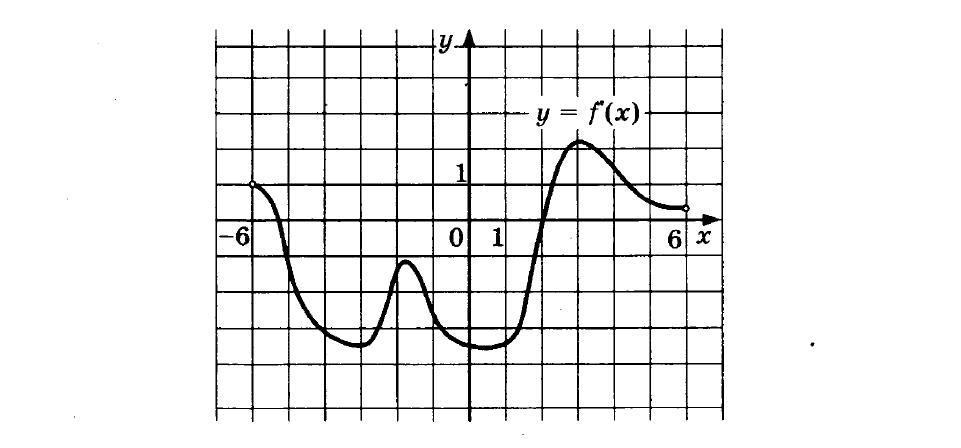
Итак, для начала следует выделить указанный отрезок. На нем функция один раз принимает нулевое значение и меняет свой знак – это точка экстремума. Так как производная из отрицательной становится положительной, значит, это точка минимума функции. Этой точке соответствует значение аргумента 2.

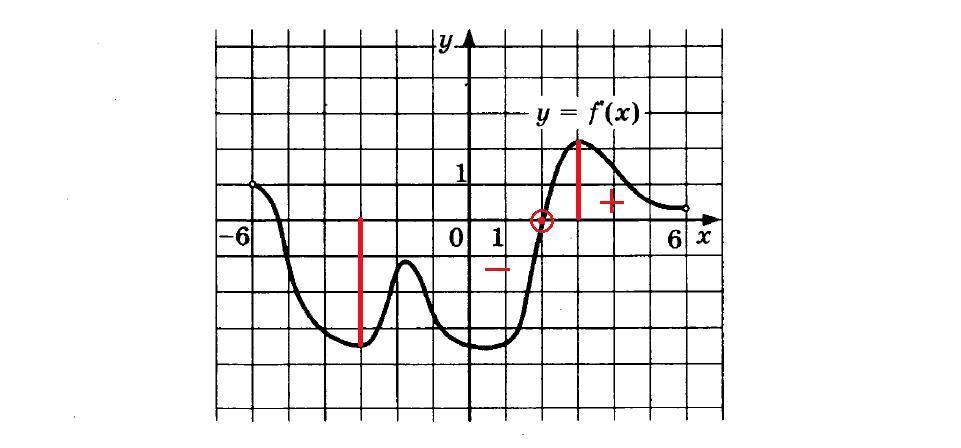
Ответ: 2.

Продолжаем рассматривать примеры. Задание: найти наибольшее и наименьшее значение функции на отрезке.

Найдите наименьшее значение функции y = (x – 8) ex-7 на отрезке [6; 8].

1. Взять производную от сложной функции.

y’ (x) = (x – 8) ex-7 = (x – 8)’ (ex-7) + (x – 8) (ex-7)’ = 1 * (ex-7) + (x – 8) (ex-7) = (1 + x – 8) (ex-7) = (x – 7) (ex-7)

2. Приравнять полученную производную к нулю и решить уравнение.

y’ (x) = 0

(x – 7) (ex-7) = 0

x – 7 = 0, или ex-7 = 0

x = 7; ex-7 ≠ 0, нет корней

3. Подставить в функцию значение крайних точек, а также полученные корни уравнения.

y (6) = (6 – 8) e6-7 = -2e-1

y (7) = (7 – 8) e7-7 = -1 * e0 = -1 * 1 = -1

y (8) = (8 – 8) e8-7 = 0 * e1 = 0

Ответ: -1.

Итак, в этой статье была рассмотрена основная теория о том, как найти наименьшее значение функции на отрезке, необходимая для успешного решения заданий ЕГЭ по профильной математике. Также элементы математического анализа применяются при решении заданий из части С экзамена, но очевидно, они представляют иной уровень сложности, и алгоритмы их решений сложно уместить в рамки одного материала.

Дорогие друзья! В  группу заданий связанных с производной входят  задачи —  в условии дан график функции, несколько точек на этом графике и стоит вопрос:

В какой точке значение производной наибольшее (наименьшее)?

Данные задачи очень просты, не требуется никаких вычислений, решаются устно. Главное что необходимо – это понимать геометрический смысл производной, свойства производной для исследования функций. По представленным ссылкам вы можете повторить (изучить) материал на сайте, также краткая информация есть в справочнике.

Кратко повторим:

Производная в точке равна угловому коэффициенту касательной проходящей через эту точку графика.

Угловой коэффициент касательной в свою очередь равен тангенсу угла наклона этой касательной.

*Имеется ввиду угол между касательной и осью абсцисс.

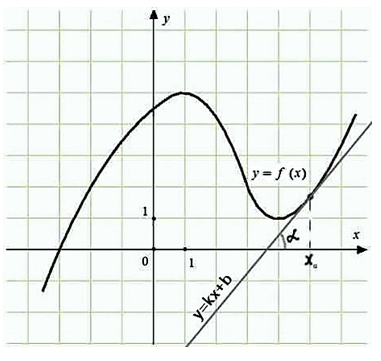
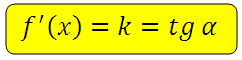
Далее:

1. На интервалах возрастания функции производная имеет положительное значение.

2. На интервалах её убывания производная имеет отрицательное значение.

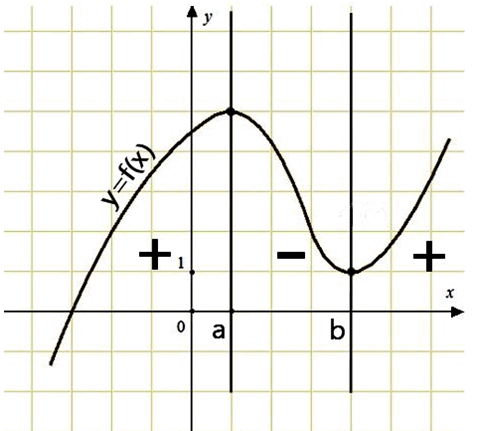
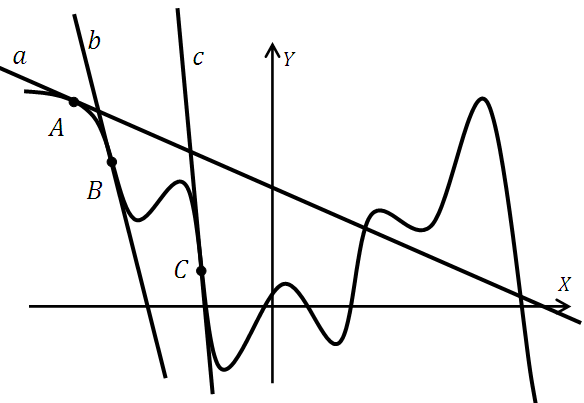
Рассмотрим следующий эскиз:

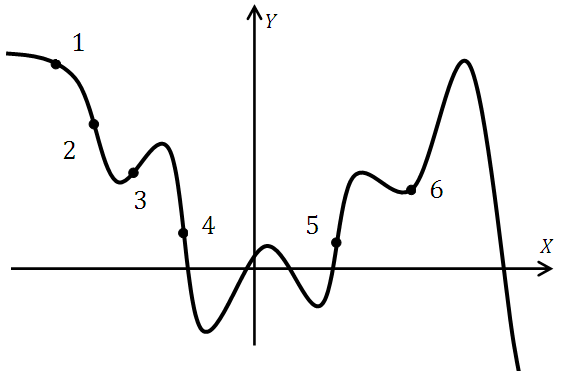
В точках 1,2,4 производная функции имеет отрицательное значение, так как данные точки принадлежат интервалам убывания.

В точках 3,5,6 производная функции имеет положительное значение, так как данные точки принадлежат интервалам возрастания.

Как видим, со значением производной всё ясно, то есть определить какой она имеет знак (положительный или отрицательный) в определённой точке графика совсем несложно.

При чём, если мы мысленно построим касательные в этих точках, то увидим, что прямые проходящие через точки  3, 5 и 6  образуют с осью оХ углы лежащие в пределах от  0 до 90^о, а прямые  проходящие через точки  1, 2 и 4   образуют с осью оХ углы в пределах от  90^о до 180^о.

*Взаимосвязь понятна: касательные проходящие через точки принадлежащие интервалам возрастания функции образуют с осью оХ острые углы, касательные проходящие через точки принадлежащие интервалам убывания функции образуют с осью оХ тупые углы.

Теперь важный вопрос!

А как изменяется значение производной? Ведь касательная в разных точках  графика непрерывной функции образует разные углы, в зависимости от того, через какую точку графика она проходит.

*Или, говоря простым языком, касательная расположена как бы «горизонтальнее» или «вертикальнее». Посмотрите:

Прямые образуют с осью оХ углы в пределах от 0 до 90^о

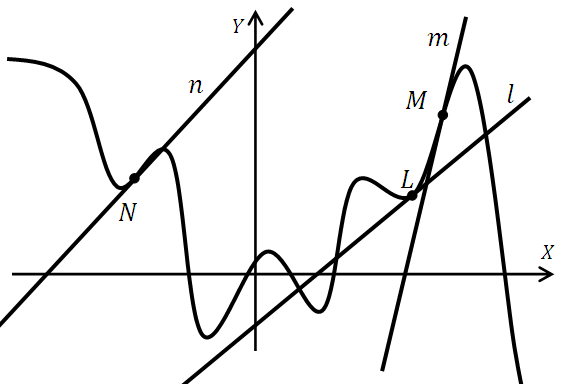
Прямые образуют с осью оХ  углы в пределах от 90^о до 180^о

Поэтому, если будут стоять вопросы:

— в какой из данных точек графика значение производной имеет наименьше значение?

— в какой из данных точек графика значение производной имеет наибольшее  значение?

то для ответа необходимо понимать, как изменяется значение тангенса угла касательной в пределах от 0 до 180^о.

*Как уже сказано, значение производной функции в точке равно тангенсу угла наклона касательной к оси оХ.

Значение тангенса изменяется следующим образом:

При изменении угла наклона прямой от 0^о до 90^о  значение тангенса, а значит и производной, изменяется соответственно от 0 до +∞;

При изменении угла наклона прямой от  90^о до 180^о   значение тангенса, а значит и производной, изменяется соответственно  –∞ до 0.

Наглядно это видно  по графику функции тангенса:

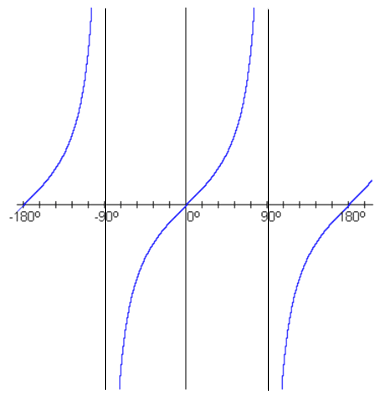
Говоря простым языком:

При угле наклона касательной от 0^о до 90^о

Чем  он  ближе к 0^о, тем  больше значение производной будет близко к нулю (с положительной стороны).

Чем  угол  ближе к 90^о, тем больше значение производной будет увеличиваться  к  +∞.

При угле наклона касательной от 90^о до 180^о

Чем  он  ближе к 90^о, тем больше значение производной будет уменьшаться к  –∞.

Чем  угол  будет ближе к 180^о, тем больше значение производной будет близко к нулю (с отрицательной стороны).

317543. На рисунке изображен график функции y = f(x)  и  отмечены точки –2, –1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

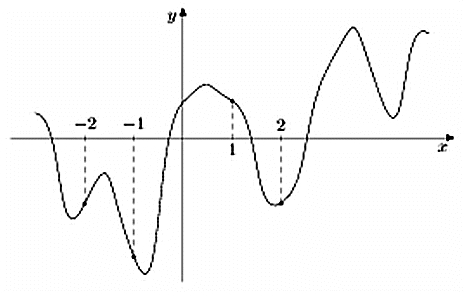
Имеем четыре точки: две из них принадлежат интервалам на которых функция убывает (это точки  –1 и 1) и две  интервалам на которых функция возрастает (это точки  –2 и 2).

Можем сразу же сделать вывод о том, что в точках –1 и 1 производная имеет отрицательное значение, в точках –2 и 2 она имеет положительное значение. Следовательно в данном случае необходимо проанализировать точки –2 и 2 и определить в какой из них  значении будет наибольшим. Построим касательные проходящие через указанные точки:

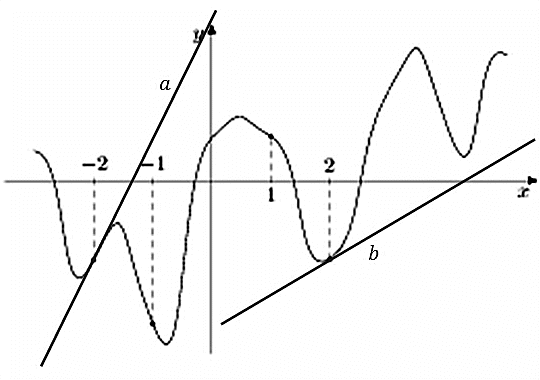
Значение тангенса угла между прямой a  и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке  –2  будет наибольшим.

Ответим на следующий вопрос: в какой из точек –2, –1, 1 или 2 значение производной является наибольшим отрицательным? В ответе укажите эту точку.

Производная будет иметь отрицательное значение в точках, принадлежащим интервалам убывания, поэтому рассмотрим точки –2 и 1. Построим касательные проходящие через них:

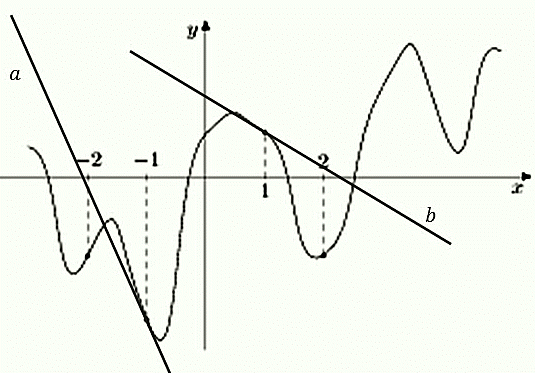
Видим, что тупой угол между прямой b и осью оХ  находится «ближе» к 180^о, поэтому его тангенс  будет больше тангенса угла, образованного прямой а и осью оХ. 

Таким образом, в точке х = 1, значение производной будет наибольшим отрицательным.

317544. На рисунке изображен график функции y = f(x)  и отмечены точки –2, –1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

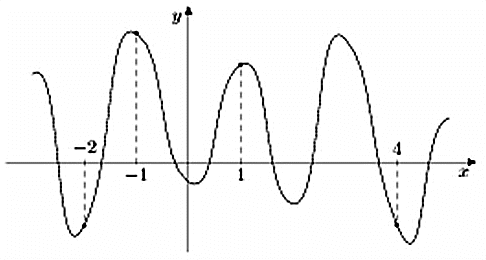
Имеем четыре точки: две из них принадлежат интервалам, на которых функция убывает (это точки  –1 и 4) и две  интервалам, на которых функция возрастает (это точки  –2 и 1).

Можем сразу же сделать вывод о том, что в точках –1 и 4 производная имеет отрицательное значение, в точках  –2 и 1 она имеет положительное значение. Следовательно, в данном случае, необходимо проанализировать точки –1 и 4 и определить – в какой из них значении будет наименьшим. Построим касательные проходящие через указанные точки:

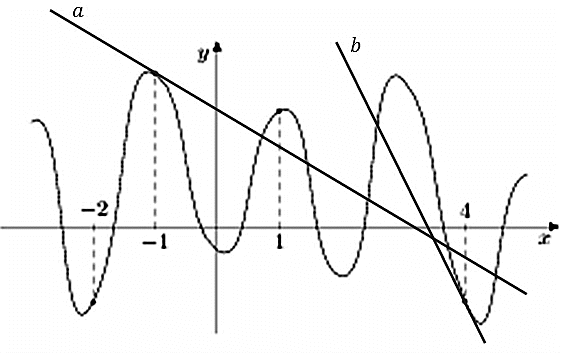
Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке  х = 4  будет наименьшим.

Ответ: 4

Надеюсь, что «не перегрузил» вас количеством написанного. На самом деле, всё очень просто, стоит только понять свойства  производной, её геометрический смысл и как изменяется значение тангенса угла от 0 до 180^о.

Общие рекомендации:

1. Сначала определите знаки производной в данных точках  (+ или -) и выберете необходимые точки (в зависимости от поставленного вопроса).

2. Постройте касательные в этих точках.

3. Пользуясь графиком тангесоиды, схематично отметьте углы и отобразите соответствующие им значения.

4. Далее в зависимости от поставленного вопроса в задаче, вы без труда определите точку.

*Если вы понимаете, как изменяется значение тангенса, то можно обойтись без  графика.

На этом всё. Успехов Вам!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.