12. Исследование функций с помощью производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Поиск наибольшего/наименьшего значения у произведения
(blacktriangleright) Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке ([a,b]), необходимо схематично изобразить график функции на этом отрезке.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).
(blacktriangleright) Не стоит забывать, что наибольшее/наименьшее значение функция может принимать не только во внутренних точках отрезка ([a,b]), а также на его концах.
(blacktriangleright) Наибольшее/наименьшее значение функции — это значение координаты (y=f(x)).
(blacktriangleright) Если функция задана как произведение двух других функций, то [{Large{(fcdot g)’=f’cdot g+fcdot g’}}]
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]
Задание
1
#2824
Уровень задания: Равен ЕГЭ
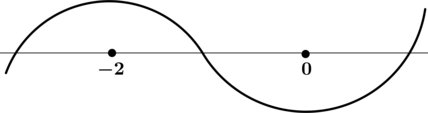
Найдите наименьшее значение функции (y = 2x^2cdot e^{x} – 3).
1) [y’ = 4xcdot e^{x} + 2x^2cdot e^{x} = 2x(x + 2)cdot e^x]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2x(x + 2)cdot e^x = 0qquadLeftrightarrowqquad x(x + 2) = 0,,] откуда находим корни (x_1 = -2), (x_2 = 0). Производная функции (y) существует при любом (x). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
По полученному эскизу нельзя сказать наверняка, действительно ли в точке локального минимума (x = 0) значение функции наименьшее, или же при каком-то отрицательном (x) значение функции окажется меньше, чем при (x = 0). Найдём (y(0)): [y(0) = 2cdot 0cdot e^{0} – 3 = -3,.] Рассмотрим произвольное (x_0 < 0), тогда [y(x_0) = 2{x_0}^2cdot e^{x_0} – 3,,] но ({x_0}^2geqslant 0) и (e^{x_0}geqslant 0), тогда [y(x_0) = 2{x_0}^2cdot e^{x_0} – 3geqslant 0 – 3geqslant -3,,] следовательно, наименьшее значение функции (y) равно (y(0) = -3).
Ответ: -3
Задание
2
#904
Уровень задания: Равен ЕГЭ
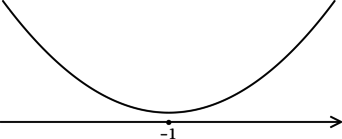
Найдите наименьшее значение функции (y = xcdot e^{x}cdot e – 11).
1) (y’ = e^{x}cdot e + xcdot e^{x}cdot e = (x + 1)cdot e^{x + 1}).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (x + 1)cdot e^{x + 1} = 0qquadLeftrightarrowqquad x = -1] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = -1) – точка минимума функции (y).
(y(-1) = -1cdot e^0 – 11 = -12),
Итого: наименьшее значение функции (y) равно (-12).
Ответ: -12
Задание
3
#905
Уровень задания: Равен ЕГЭ
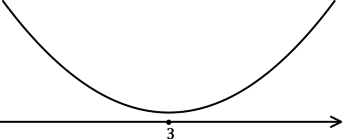
Найдите наименьшее значение функции (y = (2 – x)cdot e^{-x}cdot e^3 – 2).
1) (y’ = -e^{-x}cdot e^3 – (2 – x)cdot e^{-x}cdot e^3 = (x – 3)cdot e^{-x + 3}).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (x – 3)cdot e^{-x + 3} = 0qquadLeftrightarrowqquad x = 3] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = 3) – точка минимума функции (y).
(y(3) = -1cdot e^0 – 2 = -3),
Итого: наименьшее значение функции (y) равно (-3).
Ответ: -3
Задание
4
#909
Уровень задания: Равен ЕГЭ
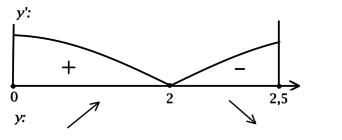
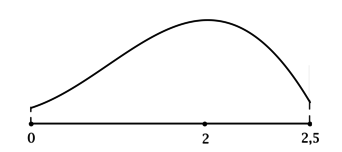
Найдите наименьшее значение функции (y = (x^2 – 14x + 34)e^{x}) на отрезке ([0; 2,5]).
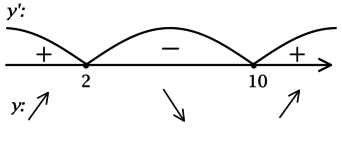
1) (y’ = (2x – 14)e^{x} + e^{x}(x^2 – 14x + 34) = e^{x}(x^2 – 12x + 20)).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad e^{x}(x^2 – 12x + 20) = 0qquadLeftrightarrowqquad x^2 – 12x + 20 = 0] (так как (e^x > 0) при любом (x) и на неё можно поделить), откуда находим корни (x_1 = 2, x_2 = 10). Таким образом, [y’ = e^{x}(x – 2)(x – 10).] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([0; 2,5]):
4) Эскиз графика на отрезке ([0; 2,5]):
Таким образом, (x = 2) – точка локального максимума функции (y) и наименьшее значение на ([0; 2,5]) функция достигает либо в (x = 0), либо в (x = 2,5). Сравним эти значения:
(y(0) = 34cdot e^0 = 34),
(y(2,5) = (6,25 – 35 + 34)e^{2,5} = 5,25cdot e^{2,5}). Так как (e > 2,7), то (5,25cdot e^{2,5} > 5,25cdot 2,7^{2,5} > 5,25cdot 2,7^{2} = 38,2725 > 34 = y(0)).
Итого: наименьшее значение функции (y) на ([0; 2,5]) равно (34).
Ответ: 34
Задание
5
#910
Уровень задания: Равен ЕГЭ
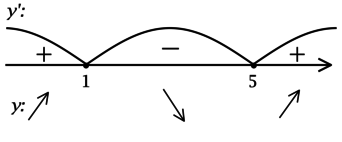
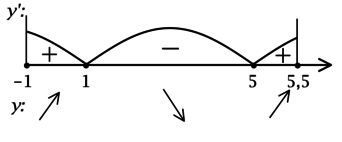
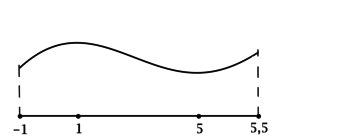
Найдите наибольшее значение функции (y = e^{-1}(x^2-8x+13)e^{x}) на ([-1; 5,5]).
Заметим, что (e^{-1}) – просто число, тогда
1) (y’ = e^{-1}((2x-8)e^{x}+e^{x}(x^2-8x+13)) = e^{-1}(x^2-6x+5)e^{x}).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad e^{-1}(x^2-6x+5)e^{x} = 0qquadLeftrightarrowqquad x^2-6x+5 = 0] (так как (e^x > 0) при любом (x) и на неё можно поделить), откуда находим корни (x_1 = 1, x_2 = 5). Таким образом, [y’ = e^{-1}(x – 1)(x – 5)e^{x}.] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-1; 5,5]):
4) Эскиз графика на отрезке ([-1; 5,5]):
Таким образом, (x = 1) – точка локального максимума функции (y), (x = 5) – точка локального минимума функции и наибольшее значение на ([-1; 5,5]) функция достигает либо в (x = 1), либо в (x = 5,5). Сравним эти значения:
(y(1) = e^{-1}(1-8+13)e^{1} = 6cdot e^{-1 + 1} = 6cdot e^{0} = 6),
(y(5,5) = e^{-1}(30,25-44+13)e^{5,5} = -0,75cdot e^{-1 + 5,5} = -0,75cdot e^{4,5} < 0 < 6 = y(1)).
Итого: наибольшее значение функции (y) на ([-1; 5,5]) равно (6).
Ответ: 6
Задание
6
#907
Уровень задания: Равен ЕГЭ
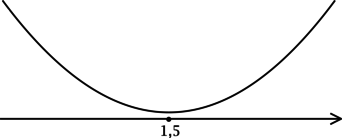
Найдите наименьшее значение функции (y = (-2x + 1)cdot e^{-x}cdot e^{1,5}).
1) (y’ = -2e^{-x}cdot e^{1,5} – (-2x + 1)cdot e^{-x}cdot e^{1,5} = (2x – 3)cdot e^{-x + 1,5}).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (2x – 3)cdot e^{-x + 1,5} = 0qquadLeftrightarrowqquad x = 1,5] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = 1,5) – точка минимума функции (y).
(y(1,5) = -2cdot e^0 = -2),
Итого: наименьшее значение функции (y) равно (-2).
Ответ: -2
Задание
7
#906
Уровень задания: Равен ЕГЭ
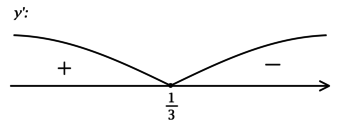
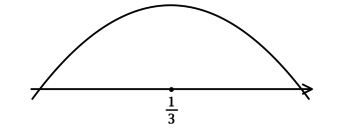
Найдите наибольшее значение функции (y = (3x + 2)cdot e^{-x}cdot e^{frac{1}{3}}).
1) (y’ = 3e^{-x}cdot e^{frac{1}{3}} – (3x + 2)cdot e^{-x}cdot e^{frac{1}{3}} = (-3x + 1)cdot e^{-x + frac{1}{3}}).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (-3x + 1)cdot e^{-x + frac{1}{3}} = 0qquadLeftrightarrowqquad x = dfrac{1}{3}] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = dfrac{1}{3}) – точка максимума функции (y).
(yleft(dfrac{1}{3}right) = 3cdot e^0 = 3),
Итого: наибольшее значение функции (y) равно (3).
Ответ: 3

УСТАЛ? Просто отдохни
Определение
Произведением чисел в математике называется результат их умножения.
Пример: Найдите произведение чисел.
14×15=210
Здесь 14 и 15 называются — множители.
Свойства
1. Коммутативность.
Пример: Вычислить произведение чисел.
17×12=204 и 12×17=204
Переместительный закон: При перестановке множителей результат не меняется.
2. Ассоциативность.
Пример:
11×19×32=6688
(11×19)×32=6688
11×(19×32)=6688
Сочетательный закон: Если группу множителей заменить их произведением, результат не изменится.
3. Дистрибутивность.
Пример:
(15+12)×9=243 и 15×9+12×9=243
Распределительный закон: Умножая сумму на число, можно на это число каждое слагаемое умножить и результаты сложить.
Большие числа, а также десятичные дроби умножают в столбик.
Нет времени решать самому?
Наши эксперты помогут!
Произведение цифр числа
Пример: найти произведение цифр числа 428
4×2×8=64
Произведение суммы и разности чисел
(23+14)×(23-14)=37×9=333
Наименьшее произведение чисел
При умножении любого числа на 0, получится ноль. Наименьшее произведение чисел равно нулю.
Сумма двух произведений чисел
(7×8)+(9×3)=56+27=83
Ответ: 83
Пример: Найди сумму и произведение чисел 14 и 72
Решение:
14+72=86 — сумма
14×72=1008 — произведение
From the 2018 Moroccan Mathematics Olympiad:
Let $(a,b) in mathbb{Z^2}$ such that $a+b$ is a solution of the equation $x^2+ax+b=0$. Find the smallest value of the product $ab$. ($mathbb Z$ contains 0)
My Approach:
I’ve solved it by an extremely bashy method, which I don’t think is worth showing. I just used the properties of quadratic equations, and basic divisibility properties. I then got all the possible solutions, and simply calculated the possible products. I found the m
Question :
Can one find the desired minimum without finding all solutions to the given equation?
Edit: Basically what I did, is find the equivalent equation: $(2a+b)^2=-b(b+2a+2)$, Now notice: $gcd(2a+b;b+2a+2)=1$ or $=2$, try all cases and get all solutions.
Edit 2: The solution given in the first edit, isn’t the long bashy solution.
Скачать материал

Скачать материал


- Сейчас обучается 389 человек из 62 регионов




- Сейчас обучается 268 человек из 65 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Методы решения задач на нахождение наибольшего и наименьшего значения величин.
(задания для учащихся 8-9 классов, углубленное изучение математики)
Чупрова О.С.
Комсомольск-на-Амуре
МБОУ лицей №1
2012 год -
2 слайд
Алгоритм изучения темы
Знакомство с понятиями прикладных задач математики.
Схема решения оптимизационных задач.
Теоремы, применяемые при решении таких задач.
Методы решения оптимизационных задач:
применение некоторых теорем;
использование свойств квадратного трехчлена;
применение неравенства Коши. -
3 слайд
Знакомство с понятиями прикладных задач математики.
Задачи на нахождение наибольшего и наименьшего значений какой-либо величины, часто применяемые в практической деятельности, называются оптимизационными. Для правильного решения таких задач необходимо выполнить их переформулировку, стремясь формализировать условия, первоначально заданные в описательной форме.
-
4 слайд
Схема решения оптимизационных задач
Проанализировав условие задачи, определить, наибольшее или наименьшее значение какой величины требуется найти (т.е. какую величину нужно оптимизировать).
Принять за независимую переменную одну из неизвестных величин и обозначить её буквой x. Определить её границы изменения.
Задать функцию y=f(x).
Найти средствами математики наибольшее или наименьшее значение на промежутке изменения х.
Интерпретировать результат для рассматриваемой задачи. -
5 слайд
Пример решения оптимизационных задач.
Число 36 записать в виде произведения двух натуральных чисел, сумма которых наименьшая.
Пусть х – первый множитель, тогда 𝟑𝟔 х – второй множитель, где 1<x<36.
Составим функцию f(x)=х+ 36 х .
Анализируя, приходим к выводу, что при х=6 составленная функция принимает наименьшее значение (6+6=12)
Ответ: 36=6·6 -
6 слайд
Теоремы и следствия из них для решения оптимизационных задач .
Теорема 1 Произведение двух положительных множителей, сумма которых постоянна, имеет наибольшее значение при равенстве множителей
(если множители могут иметь равные значения). Т.е. max xy=¼ (х+у) 𝟐
Следствие. Произведение двух положительных сомножителей х и у, связанных соотношением mx+ny=a, где m,n-положительные числа, будет наибольшим при mx=ny=a, т.е. при x=a/m; y=a/n.
Теорема 2 Сумма двух положительных слагаемых, произведение которых постоянно, имеет наименьшее значение при равенстве слагаемых.
Следствие. Если произведение ху постоянно, то mx+ny, где m,n-положительные числа, имеет наименьшее значение при mx=ny. -
7 слайд
Доказательство теорем
Теорема 1 Рассмотрим равенство, которое следует из формул сокращенного умножения, т.е.
ху = 1 4 ((х+у) 2 – (х−у) 2 ).(По условию х+у- постоянно). Произведение ху будет наибольшее при наименьшем значении (х−у) 2 , т.е. при х=у. Отметим, что
ху = 1 4 (х+у) 2 .
Теорема 2 Из тождества (х+у) 2 = (х−у) 2 +4ху ясно, что (х+у) 2 , а значит и х+у будет наибольшим, если х-у=0.
Теоремы 1 и 2 могут быть обобщены на большее число слагаемых.
Теорема 3 произведение нескольких переменных положительных сомножителей, сумма которых постоянна, достигает наибольшее значение при равенстве сомножителей (если только множители могут принимать равные значения).
Теорема 4 Если произведение положительных сомножителей х 𝟏, х 𝟐, …, х 𝐧 постоянно, то их сумма будет наибольшей, если они равны между собой. -
8 слайд
Решение оптимизационных задач с применением доказанных теорем
Задача №1 Найти наибольшее значение функции y=x³(a-x), если 0<x<a.
Решение
Т.к. сумма x³+a-х не является постоянной, то перепишем функцию в виде у = 1 3 (х·x·x(3a-3x))
Функция принимает наибольшее значение в том случае, если функция z= х·x·x(3a-3x) принимает наибольшее значение. Найдем сумму сомножителей: х+х+х+3a-3х=3a – не зависит от х, поэтому является постоянной. По теореме 3 функция z=x³(3a-3x)( а, значит, у= 1 3 z) принимает наибольшее значение в том случае, если х=3a-3x. Это получается при х= a 4 .
Mаx y=y( a 4 ) = ( a³ 4 ) ·(a- a 4 ) = 3 a 4 256 . -
9 слайд
Задача №2. Даны две параллельные прямые и точка А между ними, служащая вершиной прямого угла прямоугольного треугольника, у которого две другие вершины лежат на каждой из прямых. Какое положение должен занимать треугольник, чтобы его площадь была наибольшей?
1) Пусть ДЕ- перпендикуляр к
данным прямым. Обозначим
АД=а, АЕ=b, ЕС=х. Рассмотрим ∆ АВС,
удовлетворяющий условию задачи.
2) Построим математическую
модель задачи. Пусть ЕС=х.
Т.к. ∆ АВС – прямоугольный и проведен перпендикуляр, то
∠ЕСА+ ∠ ЕАС=90° и ∠ ЕАС+ ∠ BAД=90°, поэтому ∠ ЕСА= ∠ BAД и ∠ ЕАС= ∠ АВД =>∆EAC≈∆ДАВ, поэтому АС ЕС = АВ АД => АС х = АВ а => АС² х = АС·АВ а
Отсюда S АВС =½AC·AB=½ а·АС² х = а 2х (b²+x²)= а 2 ( b² х +х).
Т.к. а и b- постоянные, то S АВС будет наибольшим, если b² х +х будет принимать наибольшее значение. Т.о. требуется найти такое х>0, где у= b² х +х принимает наибольшее значение. Т.к. b² х ·х =b²(не зависит от х). Отсюда min S будет при х=b, т.е.ВД=а. Т.о. наибольшее значение площади будет тогда и только тогда, когда ∆EAC и ∆ДАВ равнобедренные и прямоугольные.
А
Е
С
В
Д -
10 слайд
Теорема об использовании свойств квадратного трехчлена
Преобразуем квадратичную функцию y=аx²+bx+c = а(x²+ bx а ) +с =
а(x²+ 2 b 2а х + b² 4а² – b² 4а² )+с = а(х+ b 2а )² + 4ас−b² 4а .
Отсюда следует теорема: а) если а>0, то функция y=аx²+bx+c при х=- b 2а принимает наименьшее значение, равное 4ас−b² 4а ;
б)если а<0, то функция y=аx²+bx+c при х=- b 2а принимает наибольшее значение, равное 4ас−b² 4а . -
11 слайд
Решение задач с использованием свойств квадратного трехчлена
Пример №1 Найти наименьшее и наибольшее значения функции у= 𝟐х 𝟏+х² .
решение
Дана не квадратичная функция. Поэтому рассмотрим более общую задачу: найти множество значений функции Т.е. переформулируем задание: «При каких у уравнение
у= 𝟐х 𝟏+х² относительно х имеет решение?”.
(у= 𝟐х 𝟏+х² )<=>(x²y-2x+y=0).
У=0 только при х=0. Пусть у≠0. Квадратное уравнение
уx²-2x+y=0 в этом случае имеет решение тогда и только тогда, когда D≥0.
(D≥0) <=>(4-4уу ≥0) <=>((y²≤1) <=>(-1 ≤y≤1) . Тогда множество значений данной функции совпадает с отрезком[-1;1]. Отсюда получаем: min y=y(-1)=-1; max y=y(1)=1. -
12 слайд
Пример №2. На плоскости даны три точки А,В,С, не лежащие на одной прямой. Найти на прямой ВС такую точку М, сумма квадратов расстояний которой до А,В и С была бы наименьшей.
Решение.
Проведем АД⊥ ВС и введем
обозначения АД=а, ВД=b, ДС=с
(а, b и с считать неизвестными)
МД=х, у=АМ²+BM²+CM², отсюда АМ²= АД²+MД²=x²+а²; ВМ²=(ВД-МД)²=(b-x)²; МС²=(c+x)². Получили выражение для у:
y=(a²+x²)+(b-x)²+(c+x)²=3x²-2(b-c)x+b²+c² – это квадратичная функция. Преобразуем её: У=3(х – (b−c)² 3 )²+ a²+b²+c² – (b−c)² 3 .
При х= (b−c)² 3 функция имеет наименьшее значение,
равное a²+b²+c² – (b−c)² 3 .
А
В
С
Д
М -
13 слайд
Классическое неравенство Коши
Теорема. Если а₁, а₂, …, а n −неотрицательные числа, то
а₁+а₂+ …+ а n n ≥ n а₁·а₂·… ·а n , при этом равенство выполняется тогда и только тогда, когда а₁=а₂=…= а n .
Частный случай: а+в 2 ≥ ав . -
14 слайд
Применение неравенства Коши
Из всех равновеликих треугольников найти треугольник наименьшего периметра.
Пусть х, у, z – стороны треугольника, тогда имеет место : x+y+z= 3 4 ( x+y+z 3 + x+y−z 1 + x−y+z 1 + −x+y+z 1 ). Каждое из выражений в скобках положительно, поэтому к числам x+y+z 3 ; x+y−z 1 ; x−y+z 1 ; −x+y+z 1 применим неравенство Коши при n=4. Получим:
x+y+z≥3∙ 4 x+y+z 3 · x+y−z 1 · x−y+z 1 · −x+y+z 1 = =3· 1 3 · x+y+z 2 · x+y−z 2 · x−y+z 2 · −x+y+z 2 = 3· 1 3 S = 3 S
Отсюда следует, что наименьшее значение периметра равно 𝟑 S и достигается при х=у=z. -
15 слайд
Решить самостоятельно.
Окно имеет форму прямоугольника, завершенного полукругом. Дан периметр фигуры. Каковы должны быть размеры окна, чтобы оно пропускало наибольшее количество света? (ответ: 2Р 4+𝜋 ; 2Р 4+𝜋 ).
Найти наименьшее значение функции у= х х²+1 , х>0. (ответ: min y=-1/2 при х=-1).
Найти наименьшее значение функции у= х² – 6х + 5. (ответ: min y=-4 при х=3).
Через точку М, лежащую внутри заданного угла, проводятся различные прямые. Определить ту из прямых, которая отсекает от сторон угла треугольник наименьшей площади. (ответ: min S=- (max z)² = у(3)= -4).
Используя неравенство Коши, найти: а)наименьшее значение функции у=х+ 4 х , где х>0; б) наибольшее значение функции
у= 2х 1+х² ( ответ: а) при х=2 min y=4 ; б) max y=1 при х=1) -
16 слайд
Используемая литература.
И.Я. Виленкин и др. Алгебра и математический анализ для 9 класса. М. Просвещение. 1983.
В.В. Мельников и др. Начала анализа. М. Наука. 1990.
Н.И. Зильберберг. Алгебра и начала анализа в 10 классе. Для углубленного изучения математики. Псков. 1994.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 262 023 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Тест по Новой истории Латинской Америки
- Учебник: «Всеобщая история. Новейшая история», Юдовская А.Я., Баранов П.А., Ванюшкина Л.М. и др./Под ред. Искендерова А.А.
- Тема: Глава 3. Азия, Африка и Латинская Америка в XIX – начале ХХ в.
- 11.01.2021
- 6320
- 138

Отчет работы кружка “Дари добро”
- Учебник: «Экономика: история и современная организация хозяйственной деятельности», Липсиц И.В.
- Тема: Тема 2. Как устроена хозяйственная жизнь человечества
- 11.01.2021
- 2894
- 1

- 11.01.2021
- 2681
- 0
- 11.01.2021
- 2713
- 0
- 11.01.2021
- 2963
- 3

- 11.01.2021
- 2996
- 1
- 11.01.2021
- 2710
- 0
Вам будут интересны эти курсы:
-
Курс профессиональной переподготовки «Организация и предоставление туристских услуг»
-
Курс повышения квалификации «Экономика и право: налоги и налогообложение»
-
Курс повышения квалификации «Введение в сетевые технологии»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС технических направлений подготовки»
-
Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
-
Курс повышения квалификации «Финансы: управление структурой капитала»
-
Курс повышения квалификации «Психодинамический подход в консультировании»
-
Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»
-
Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»
-
Курс повышения квалификации «Финансовые инструменты»
-
Курс профессиональной переподготовки «Техническая диагностика и контроль технического состояния автотранспортных средств»
-
Курс профессиональной переподготовки «Теория и методика музейного дела и охраны исторических памятников»
-
Курс профессиональной переподготовки «Стратегическое управление деятельностью по дистанционному информационно-справочному обслуживанию»