Ученик
(64),
закрыт
9 лет назад
Naumenko
Высший разум
(856084)
9 лет назад
д=9 из а2-а1
формула а1+д (н-1)>0
решается подстановкой известного относительно н
проверяете. что при полученном н (нужно натуральное значение взять в большую сторону ) .а с номером н положительно и это все.
Булатова Римма
Искусственный Интеллект
(126407)
9 лет назад
d=a2-a1=(-81)-(-100)=19.
a(n)=a1+d(n-1); a(n)=-100+19(n-1); a(n)=19n-119. a(n)>=1; 19n-119>=1; 19n>=120; n>=120/19; n>=6,3. Но т. к. n должно быть целым числом, то отвечать этому решению будет n=7. а (7)=14 будет наименьшим положительным членом заданной прогрессии.
Комментарии преподавателя
На этом уроке мы рассмотрим арифметическую прогрессию и ее свойства.
Вначале дадим определение арифметической прогрессии и приведем ряд примеров. Далее выведем формулу n-го члена арифметической прогрессии и докажем, что арифметическая прогрессия – это линейная функция. В конце решим ряд примеров на пройденный материал.
Тема: Прогрессии
Урок: Определение и свойства арифметической прогрессии, формула n-го члена
1. Определение арифметической прогрессии
Вспомним, что числовая последовательность – частный случай функции, функции, определенной на множестве натуральных чисел. Арифметическая прогрессия – частный случай числовой последовательности.
Рассмотрим примеры, дающие представление об арифметической прогрессии.
1. Задана последовательность чисел: 
Закономерность образования данной последовательности: каждый последующий член больше предыдущего на 4 (обозначим это число буквой d), т.е. 
 Данную последовательность можно задать рекуррентно:
Данную последовательность можно задать рекуррентно:  . Заметим, что эта последовательность является возрастающей (
. Заметим, что эта последовательность является возрастающей ( ) .
) .
2. Задана последовательность чисел:  В этой последовательности все числа равны между собой,
В этой последовательности все числа равны между собой,  .
.
3. Задана последовательность чисел: 
Закономерность образования данной последовательности: каждый последующий член меньше предыдущего на 2. Чтобы получить последующий член надо к предыдущему прибавить число (-2), т.е. 
 Данную последовательность можно задать рекуррентно:
Данную последовательность можно задать рекуррентно:  . Заметим, что эта последовательность является убывающей (
. Заметим, что эта последовательность является убывающей ( ) .
) .
Дадим определение арифметической прогрессии.
Числовая последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называется арифметической прогрессией, число d называется ее разностью.
Арифметическая прогрессия обозначается следующим образом: .
.
Арифметическая прогрессия может быть задана рекуррентно: 
Непосредственно из определения арифметической прогрессии следуют такие свойства:
– если  , то арифметическая прогрессия
, то арифметическая прогрессия  – возрастающая;
– возрастающая;
– если  , то арифметическая прогрессия
, то арифметическая прогрессия  – убывающая.
– убывающая.
2. Формула n-го члена арифметической прогрессии
Из определения арифметической прогрессии следует истинность равенств:  . Тогда
. Тогда


 и т.д. Значит,
и т.д. Значит, 
Т.е., зная первый член и разность арифметической прогрессии, можно найти любой ее член.
Арифметическую прогрессию считают заданной, если известен ее первый член и разность.
Формулу  называют формулой n-го члена арифметической прогрессии.
называют формулой n-го члена арифметической прогрессии.
3. Доказательство формулы n-го члена арифметической прогрессии
Формулу n-го члена арифметической прогрессии можно доказать с помощью метода математической индукции.
Дано:  ,
,  .
.
Доказать:  (1)
(1)
Доказательство.
Формула (1) верна при n=1. Действительно,  .
.
Предположим, что формула (1) верна при n=k, т.е.  .
.
Докажем, что формула (1) верна и при n=k+1, т.е.  .
.
Из условия  и предположения
и предположения  получаем:
получаем:
 .
.
Согласно принципу математической индукции формула (1) верна для любого натурального числа.
4. Исследование арифметической прогрессии
Из формулы n-го члена арифметической прогрессии следует, что
 . Это означает, что арифметическая прогрессия зависит от n, т.е. является функцией натурального аргумента.
. Это означает, что арифметическая прогрессия зависит от n, т.е. является функцией натурального аргумента.
Вывод: арифметическая прогрессия – это линейная функция натурального аргумента  , где
, где  .
.
Если  , то линейная функция возрастает и арифметическая прогрессия
, то линейная функция возрастает и арифметическая прогрессия  – возрастающая;
– возрастающая;
если  , то линейная функция убывает и арифметическая прогрессия
, то линейная функция убывает и арифметическая прогрессия  – убывающая.
– убывающая.
5. Примеры
Пример 1.
Дано:  =
= .
.
Найти: формулу n-го члена арифметической прогрессии  .
.
Доказать:  – возрастающая.
– возрастающая.
Дать: геометрическую иллюстрацию.
Решение.
 .Тогда
.Тогда  , т.е.
, т.е.  .
.
Поскольку  , заданная арифметическая прогрессия – возрастающая.
, заданная арифметическая прогрессия – возрастающая.
Чтобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции  и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 1).
и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 1).

Рис. 1. График функции 
Пример 2.
Дано:  =
= .
.
Найти: формулу n-го члена арифметической прогрессии  .
.
Дать: геометрическую иллюстрацию.
Решение.
 .
.
Тогда  для любого натурального числа.
для любого натурального числа.
Чтобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции  и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 2).
и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 2).

Рис. 2. График функции 
Пример 3.
Дано:  =
= .
.
Найти: формулу n-го члена арифметической прогрессии  .
.
Доказать:  – убывающая.
– убывающая.
Дать: геометрическую иллюстрацию.
Решение.
 .
.
Тогда  , т.е.
, т.е.  .
.
Поскольку  , заданная арифметическая прогрессия – убывающая.
, заданная арифметическая прогрессия – убывающая.
Чтобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции  и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 3).
и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 3).

Рис. 3. График функции 
Пример 4.
Дано:  ,
,  .
.
Найти:  ; наименьший положительный член.
; наименьший положительный член.
Решение.
Формула n-го члена арифметической прогрессии:  .
.
Тогда  , т.е.
, т.е.  .
.
Чтобы найти наименьший положительный член, надо опять воспользоваться формулой n-го члена арифметической прогрессии.
 . Тогда
. Тогда  , и значит
, и значит  .
.
Наименьший положительный член прогрессии  .
.
Ответ:  ;
;  – наименьший положительный член.
– наименьший положительный член.
Пример 5.
Дано:  ,
,  .
.
Найти:  .
.
Решение.
Формула n-го члена арифметической прогрессии:  .
.
Тогда  ,
,  ,
,  .
.
Ответ:  .
.
Урок: Формула суммы членов конечной арифметической прогрессии
1. Вступление
Рассмотрим задачу: найти сумму натуральных чисел от 1 до 100 включительно.
Дано: 1, 2, 3, …, 98, 99, 100.
Найти: S100=1+2+3 … +98 + 99 + 100.
Решение: S100=(1+100)+(2+99)+(3+98)+…+(50+51)=101+101+101+…+101=101 х 50=5050.
Ответ: 5050.
Последовательность натуральных чисел 1, 2, 3, …, 98, 99, 100 является арифметической прогрессией: а1=1, d=1.
Мы нашли сумму первых ста натуральных чисел, т.е. сумму первых n членов арифметической прогрессии.
Рассмотренное решение предложил великий математик Карл Фридрих Гаусс, живший в 19 веке. Задача была им решена в возрасте 5-ти лет.

Историческая справка: Иога́нн Карл Фри́дрих Га́усс (1777 — 1855) — немецкий математик, механик, физик и астроном. Считается одним из величайших математиков всех времён, «королём математиков». Лауреат медали Копли (1838), иностранный член Шведской (1821) и Российской (1824) Академий наук, английского Королевского общества. Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных в одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 101×50=5050.
2. Вывод формулы суммы первых n членов арифметической прогрессии
Рассмотрим аналогичную задачу для произвольной арифметической прогрессии.
Дано:  :
: 
Найти: сумму первых n членов арифметической прогрессии.
Решение:



Покажем, что все выражения в скобках равны между собой, а именно выражению  . Пусть d – разность арифметической прогрессии. Тогда:
. Пусть d – разность арифметической прогрессии. Тогда:
 ;
;
 ; и т.д. Следовательно, мы можем записать:
; и т.д. Следовательно, мы можем записать:
 . Откуда получаем формулу суммы первых n членов арифметической прогрессии:
. Откуда получаем формулу суммы первых n членов арифметической прогрессии:
 .
.
3. Решение задач на применение формулы суммы первых n членов арифметической прогрессии
1. Решим задачу о сумму натуральных чисел от 1 до 100 с помощью формулы суммы первых n членов арифметической прогрессии:
Решение: а1=1, d=1, n=100.
Общая формула:
 .
.
В нашем случае:  .
.
Ответ: 5050.
2. Дано:  .
.
Найти:  .
.
Решение.
Общая формула:
 . Найдем
. Найдем  по формуле n–го члена арифметической прогрессии:
по формуле n–го члена арифметической прогрессии:  .
.
 .
.
В нашем случае:  .
.
Ответ:  .
.
3. Дано:  .
.
Найти:  .
.
Решение:
Чтобы найти  , сначала надо найти
, сначала надо найти  .
.
Это можно сделать по общей формуле  .Сначала применим эту формулу для нахождения разности арифметической прогрессии.
.Сначала применим эту формулу для нахождения разности арифметической прогрессии.
 , т.е.
, т.е.  . Значит
. Значит  .
.
Теперь можем найти  .
.
 .
.
Используя формулу суммы первых n членов арифметической прогрессии
 , найдем
, найдем  .
.
 .
.
 .
.
Ответ:  .
.
4. Вывод второй формулы суммы первых n членов арифметической прогрессии
Получим вторую формулу для суммы первых n членов арифметической прогрессии, а именно: докажем, что  .
.
Доказательство:
В формулу суммы первых n членов арифметической прогрессии  подставим выражение для
подставим выражение для  , а именно
, а именно  . Получим:
. Получим:  , т.е.
, т.е.  . Что и требовалось доказать.
. Что и требовалось доказать.
Проанализируем полученные формулы. Для вычислений по первой формуле  надо знать первый член, последний член и n по второй формуле
надо знать первый член, последний член и n по второй формуле  – надо знать первый член, разность и n.
– надо знать первый член, разность и n.
И в заключение заметим, что в любом случае Sn– это квадратичная функция от n, потому что  .
.
5. Решение задач на применение второй формулы суммы первых n членов арифметической прогрессии
1. Дано:  .
.
Найти:  .
.
Решение:
Общая формула:
 .
.
В нашем случае: .
.
Ответ: 403.
2. Найти сумму всех двузначных чисел, кратных 4.
Решение:
{12; 16; 20; …; 96} – множество чисел, удовлетворяющих условию задачи.
Значит, имеем арифметическую прогрессию  .
.
n найдем из формулы для  :
: .
.
 , т.е.
, т.е.  . Значит
. Значит  .
.
Используя вторую формулу суммы первых n членов арифметической прогрессии
 , найдем
, найдем  .
.
 .
.
Ответ:  .
.
3. Дано:  .
.
Найти: S= .
.
Требуется найти сумму всех членов с 10 по 25-й включительно.
Один из способов решения заключается в следующем:
 .
.
Следовательно,  .
.
 .
.
 .
.
 .
.
Ответ:  .
.
Источник конспекта: http://interneturok.ru/ru/school/algebra/9-klass/progressii/opredelenie-i-svoystva-arifmeticheskoy-progressii-formula-ee-n-go-chlena?konspekt&chapter_id=38
Источник видео: http://www.youtube.com/watch?v=tQEVKFGcjL0
-
Алгебра
Предыдущий вопрос
Следующий вопрос
THEPIKACHUUHD
4 года назад
Ответ
Проверено экспертом
Ответ дан
mmb1
a1 = -26
d=a2 – a1 = -20 – (-26) = -20 + 26 = 6
an=a1 + d(n-1) > 0
-26 + 6(n -1) > 0
-26 + 6n – 6 > 0
6n > 32
n > 32/6 ≈ 5.33
так как n – число наткральное
n = 6
начиная с 6-го
Ответы и объяснения
- THEPIKACHUUHD
Не тот ответ, который тебе нужен?
Найди нужный
Для нецелочисленной прогрессии решения нет (оно равно минус бесконечности).
При условии целочисленности прогрессии:
s = int(input())
if s <= 0: print(s)
else: print(-s+1)
На случай, если прогрессия не только целочисленна, но и неотрицательна (и такова же и ее сумма, понятно)…
Первый член прогрессии a связан с суммой S и числом членов n формулой

Очевидно, что чтобы a было целым, надо либо чтобы S делилось нацело на n и n было нечетным, либо n четно, но тогда 2S должно делиться на n.
Так что надо просто поискать соответствующие n в диапазоне [1,2S].
Проще всего — переборно, единственным циклом (условие же — без вложенных :))
Т.е. что-то типа (сделано топорно из-за слабого знания питона, по сути перевод с С плюс отсутствие оптимизации (тупой перебор). Кто умеет — можете смело исправлять код):
def a(S: int):
m: int
m = S
for n in range(2,2*S+1):
q = 2*S-n*(n-1)
if q < 0: break
if q%(2*n) == 0:
q = q / (2*n)
if q < m: m = q
return m
s = int(input())
print(int(a(s)))
Суперполезная формула! Позволяет легко и просто (и главное — быстро!) искать любой член арифметической прогрессии! Да-да, любой! Какой хотите.) А заодно и массу других самых разных задач по прогрессии решать. Имеет смысл освоить и разобраться, правда?
Вот поэтому осваиваем и разбираемся. В этом уроке.)
Вывод и смысл формулы n-го члена
Итак, прошу любить и жаловать:
an = a1 + (n-1)·d
Это и есть формула n-го члена арифметической прогрессии, собственной персоной.) Какие-то индексы, буковки непонятные. Ничего страшного! Сейчас всё расшифрую.
В формуле:
a1 — первый член арифметической прогрессии;
d — разность арифметической прогрессии;
n — номер члена;
an — энный (n-й) член арифметической прогрессии.
Как вы видите, большая часть входящих в формулу буковок (первый член, разность прогрессии, номер члена) уже должна быть вам хорошо знакома из прошлого урока. Если не читали, настоятельно рекомендую заглянуть. Там всё просто и доступно. Осталось лишь разобраться, что же такое n-й член.
Мы с вами знаем (надеюсь), что любую арифметическую прогрессию в общем виде всегда можно записать в виде последовательности чисел:
a1, a2, a3, a4, a5, …
Символ a1 означает первый член прогрессии, a2 — второй член, a5 — пятый и так далее. Если нас интересует, скажем, десятый член прогрессии, то работаем с a10. Если сто тридцатый, то, соответственно, с a130. Элементарно, Ватсон!)
А как можно обозначить в общем виде любой член арифметической прогрессии прогрессии с любым номером? Тоже элементарно! Вот так:
an
Это и есть n-й член арифметической прогрессии. Под буковкой n здесь скрываются сразу все номера членов: и 1, и 23 и 101 — все без исключения!
И что нам даёт такая запись? Казалось бы, всего лишь вместо цифры буковка появилась — и что из этого? А вот что.
Запись эта представляет собой очень мощный инструмент для работы с арифметической прогрессией. Сомневаетесь? Не надо.) Используя обозначение an, мы можем легко и просто искать любой член любой арифметической прогрессии! Как? Читаем дальше.)
Возвращаемся снова к нашей формуле:
an = a1 + (n-1)·d
Со всеми обозначениями мы успешно разобрались, а теперь разбираемся, в чём же её суть.
Эта формула позволяет нам найти любой член арифметической прогрессии по его номеру “n“.
Заманчиво, правда? Знаем номер члена — сразу же можем найти и сам этот член! Естественно, для этого нам надо знать ещё первый член a1 и разность прогрессии d. Ну так без этих двух ключевых параметров конкретную прогрессию и не задашь вовсе.
Формула эта связывает четыре главных параметра любой арифметической прогрессии — аn, a1, d и n. Именно вокруг этих четырёх параметров и крутятся все-все задачки по прогрессии!
Откуда же берётся эта формула и как её запомнить? А то уж больно часто сомнения грызут — то ли n там, то ли n-1, то ли n+1… Особенно на контрольных и экзаменах.
Спокойствие! Сейчас мы с вами эту формулку выведем! Не очень строго, правда, но зато с полным пониманием всего происходящего. Что, как и откуда. И у вас сразу же отпадут все сомнения!
Итак, рисуем числовую ось и последовательно отмечаем на ней члены нашей прогрессии:
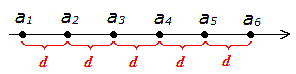
А теперь смотрим на рисунок и соображаем. Чему равен второй член прогрессии?
Второй член равен первому члену плюс одно d:
a2 = a1 + 1·d
А третий член чему равен?
Не вопрос! Третий член равен первому члену плюс два d:
a3 = a1 + 2·d
Ну как, улавливаете закономерность? Я же не просто так некоторые слова и цифры выделяю жирным шрифтом! Нет? Что ж, ладно. Ещё один шаг.)
Чему равен четвёртый член?
Четвёртый член равен первому члену плюс три d:
a4 = a1 + 3·d
Пора бы уже догадаться, что количество интервалов (т.е. d) всегда на единичку меньше, чем номер нужного нам члена n. Поэтому до номера n количество интервалов всегда будет n-1.
Стало быть, наша формула, уже безо всяких сомнений, будет вот такой:
an = a1 + (n-1)·d
Вот и весь секрет.)
Совсем строгое доказательство данной формулы проводится так называемым методом математической индукции. Но метод этот — для особых гурманов.) Не каждый с ходу разберётся и поймёт, что к чему. А вот по картинке всё просто и наглядно! Да и вообще, картинка — очень мощный инструмент решения многих математических задач! И не только по прогрессиям. Так что не пренебрегаем ими. Скажем, в сложной боевой обстановке ЕГЭ вы переволновались и подзабыли случайно эту формулу. Ну, вот не помните, с кем не бывает! Ничего страшного. Есть пара-тройка минуток времени – рисуем картинку, отмечаем члены прогрессии и промежутки между членами — и всё сразу становится как на ладони!
Разумеется, всё от конкретной задачи зависит. Бывают и такие задачи, рисовать картинку к которым весьма затруднительно, а то и вовсе невозможно. Тогда — только формула, да…) Ибо формула — это тяжёлая артиллерия, позволяющая подключить к решению задачи весь мощный арсенал математики — уравнения, неравенства, системы и т.д. Картинку ведь в уравнение не вставишь!
Ну что, коли уж мы заговорили о задачках, то пора бы уже и порешать!
Решение задач с помощью формулы n-го члена арифметической прогрессии.
Прямое применение формулы.
Начнём с прямого применения формулы. В самом конце прошлого урока была вот такая задачка:
В арифметической прогрессии известно, что a1 = 4 и d = 0,4. Найдите a141.
Конечно, эту задачку можно и безо всяких формул решить. Исходя из смысла арифметической прогрессии. Прибавлять себе по 0,4 да считать. Часок-другой…)
Зато по формуле решение осуществляется в одну строчку и занимает меньше минуты! Можете засекать время.)
Итак, у нас имеются все данные для применения формулы.
Известен первый член: a1 = 4.
Известна также разность прогрессии: d = 0,4.
Остаётся только сообразить, чему равен номер члена n. Не вопрос! Нам надо найти a141. Так прямо и пишем:
a141 =
А вот здесь сосредотачиваемся! Вместо индекса n у нас появилось конкретное число 141. Что вполне естественно. Ибо нас интересует член прогрессии номер сто сорок один. Вот именно это и будет наше n! Именно это значение n = 141 мы и подставим в формулу n-го члена в скобки.
Подставляем все наши данные в формулу и считаем:
a141 = 4 + (141-1)·0,4 = 4+56 = 60
Вот и всё, никаких фокусов. Так же быстро можно найти и четыреста третий член, и тысяча первый — любой! Какой хотим, такой и отыщем. Просто подставляем нужный номер в формулу вместо индекса n и в скобки. И считаем.)
Рассмотрим теперь задачку похитрее.
В арифметической прогрессии с разностью 3 пятнадцатый член равен 50. Найдите первый член этой прогрессии.
Ну и как вам? Знаете, с чего начинать? Если знаете — вперёд и с песнями. Не знаете? Что ж, тогда подскажу.
Пишем формулу n-го члена арифметической прогрессии!
Да-да! Прямо на черновике или в тетрадке.)
an = a1 + (n-1)·d
А теперь глядим внимательно на нашу формулу и соображаем, какие данные у нас уже есть, а чего не хватает.
Во-первых, нам известна разность прогрессии d:
d = 3
Во-вторых, нам известен пятнадцатый член прогрессии. Так и пишем:
a15 = 50
Всё? Не-а! У нас есть ещё номер n! Дело в том, что в условии a15 = 50 скрыты сразу два параметра прогрессии. Это, во-первых, значение самого пятнадцатого члена (50) и, во-вторых, его номер (15). То есть, n=15.
Вот теперь уже можно подставить все известные нам данные в формулу:
50 = a1 + 3·(15-1)
Решаем это простенькое линейное уравнение и получаем ответ:
a1 = 8
Вот и все дела.)
Ещё одна популярная задачка:
Найдите разность арифметической прогрессии (an), если
a1 = 6; a21 = -14.
Первый шаг тот же самый: пишем формулу n-го члена арифметической прогрессии!
an = a1 + (n-1)·d
А теперь снова соображаем, что нам дано по условию задачи:
a1 = 6
a21 = -14
n = 21
Вот и всё. Всю ценную информацию из условия скачали. Подставляем наши известные величины в формулу и считаем банальную арифметику:
-14 = 6 + (21-1)·d
-14 = 6 + 20d
-20 = 20d
d = -1
Всё. Это правильный ответ.)
Так, задачки на поиск an, a1 и d порешали. Осталось научиться ещё номер члена находить.)
Известно, что число 43 является членом арифметической прогрессии (an) c первым членом, равным 3 и разностью 0,4. Найдите номер этого члена.
Вы удивитесь, но первый шаг снова точно такой же.
Пишем формулу!
an = a1 + (n-1)·d
На первый взгляд кажется, что здесь две неизвестные величины — an и n. Но an — это какой-то член арифметической прогрессии под номером n. И этот член нам известен! Это 43. Нам неизвестен номер n этого члена. Так этот самый номер, как раз, и требуется отыскать!
Подставляем член прогрессии 43 в формулу n-го члена вместе с остальными известными нам параметрами:
43 = 3 + (n-1)·0,4
Считаем простецкую арифметику и выражаем номер n:
(n-1)·0,4 = 40
n-1 = 100
n = 101
Готово дело.)
Как вы видите, запись формулы в общем виде и подстановка в неё известных величин — весьма популярный приём в решении очень многих задач на прогрессии! Если вы, конечно, умеете выражать переменную из формулы. Ну так без этого умения математику можно и вовсе не изучать. Как, впрочем, и остальные точные науки тоже, да…
А теперь ещё одна задачка на эту тему, но более творческая.
Определите, будет ли число 74 членом арифметической прогрессии
(an): -5,6; -4; -2,4; …
Снова (да-да!) пишем формулу:
an = a1 + (n-1)·d
Начинаем подставлять известные нам данные. Гм… не подставляется что-то…
Что, не видите никаких данных? Серьёзно? Ну, тогда срочно к окулисту. Без обид.) Что же всё-таки можно увидеть из предложенной нам последовательности? Первый член видим? Видим! Это -5,6. А разность d? Пока не видим, но… её можно посчитать, да.) Если, конечно, вы в курсе, что такое разность арифметической прогрессии:
d = -4 — (-5,6) = 1,6
Ну вот, уже кое-что. Осталось лишь разобраться с неизвестным нам номером n и загадочным числом 74. В предыдущей задачке нам прямым текстом было указано, что дан именно член прогрессии. А здесь про число 74 ничего непонятно — член оно, не член… Что делать?
Что-что… Включим смекалку! Мы предположим, что число 74 — это всё-таки член нашей прогрессии! С неизвестным номером n. И снова попробуем отыскать, найти этот номер! Смело подставляем в формулу все наши числа:
74 = -5,6 + (n-1)·1,6
И выражаем n:
(n-1)·1,6 = 79,6
n — 1 = 49,75
n = 50,75
Во как! Номер получился дробный! А дробных номеров в прогрессиях не бывает. Уравнению ведь без разницы, с какими числами работать — целыми, дробными, отрицательными. Уравнение со всякими работает.) Вот оно нам честно и ответило: “В этой арифметической прогрессии число 74 имеет номер 50,75!”
И какой же вывод можно сделать из полученного результата? Да! Число 74 не является членом нашей прогрессии! Оно находится где-то между пятидесятым и пятьдесят первым членами. Вот, если бы наш номер получился натуральным, то тогда — да, число 74 было бы членом нашей прогрессии. С найденным номером n.
А так, ответ задачи: нет.
Более сложные задачи.
Рассмотрим теперь более хитрые задачки на применение формулы n-го члена. Например, такую:
Известно, что в арифметической прогрессии a3 = 2,1 и a6 = 6,3. Найдите a4.
Эту задачку мы с вами уже решали в прошлом уроке. Для её успешного решения мы рисовали с вами вот такую незамысловатую картинку:
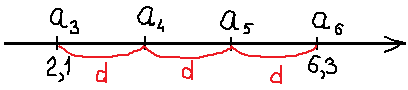
Из этой картинки мы легко определили разность прогрессии d и затем так же легко, прямо по смыслу арифметической прогрессии, посчитали нужный нам четвёртый член.
Получили ответ: a4 = 3,5.
Вспомнили? Отлично!
То был графический способ. А сейчас мы с вами решим эту же задачку, но другим способом! Аналитическим.) С помощью формулы n-го члена, да. Нам ведь с формулой размяться нужно, правда?) Вот и разминаемся.
Итак, что нам дано в условии задачи? Нам даны два члена некоторой арифметической прогрессии. А именно — третий и шестой её члены.
Вот и расписываем их по формуле n-го члена!
Именно так! Просто берём формулу n-го члена арифметической прогрессии и поочерёдно подставляем в неё известные нам данные для каждого члена.
Для третьего члена a3 = 2,1 получим:
2,1 = a1 + (3-1)·d
2,1 = a1 + 2d
Так, отлично. Одно уравнение составилось.
То же самое проделываем и для шестого члена a6 = 6,3.
Получим:
6,3 = a1 + (6-1)·d
6,3 = a1 + 5d
Итак, мы получили два уравнения. Эти два уравнения относятся к одной и той же прогрессии. Стало быть, они должны выполняться одновременно. И, следовательно, они должны быть записаны в виде системы уравнений.
Вот так:
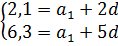
Всё. Мы перевели задание по арифметической прогрессии в чистую алгебру. И дальше можно уже временно вообще забыть про прогрессию и просто решить эту систему уравнений.
Системка не самая трудная. Решаем самым простым способом — подстановкой. Из первого уравнения выражаем a1 и подставляем во второе:
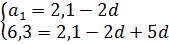
Приводим подобные во втором уравнении и получаем:
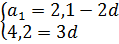
Из второго уравнения легко находится d:
d = 1,4
Подставляем d = 1,4 в первое уравнение и получаем первый член:
a1 = 2,1-2·1,4
a1 = 2,1-2,8
a1 = -0,7
Вот и отлично. Знаем первый член a1, знаем разность d. И теперь мы без проблем можем найти любой интересующий нас член прогрессии. В том числе и четвёртый, да.)
Пишем формулу n-го члена для n = 4:
a4 = a1 + (4-1)·d = a1 + 3d
Подставляем найденные числа и считаем:
a4 = a1 + 3d = -0,7+3·1,4 = -0,7+4,2 = 3,5
Вот и всё. Как и следовало ожидать, ответ получился тем же самым.)
Ну как, хлопотно? Да, я согласен. Но зато аналитическому способу (алгебре) любые задачи по плечу! Если её знать, конечно.) А вот картинка годится лишь для маленьких кусочков прогрессии.
Например, такая задачка:
Известно, что в арифметической прогрессии a81 = 26 и a271 = 83. Найдите a11.
Что, неохота картинку рисовать да безошибочно пальчиком считать промежутки? И правильно! Не надо.) Зато второму способу, алгебре, совершенно безразлично, какие числа стоят в задании! Большие числа или маленькие… Алгебра — это тяжёлая артиллерия. С любыми числами справляется.)
Снова, как и в предыдущей задаче, расписываем каждый член прогрессии по формуле n-го члена:
26 = a1 + 80d
83 = a1 + 270d
Объединяем эти уравнения в систему:
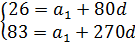
А дальше решаем точно так же, как и в предыдущей задаче. Один в один. Дорешайте, чего уж там!
Должно получиться:
a11 = 5
Рассмотрим ещё более хитрую задачку. С подвохом. Если невнимательно читать задание…
Сумма первого и седьмого членов возрастающей арифметической прогрессии равна 14, а произведение третьего и шестого членов равно 10. Найдите двадцатый член прогрессии.
Что, внушает? Решение по картинке и “на пальцах” не катит, да… Попробуем перевести всё задание в чистую алгебру? А та — всё сможет.)
Ничего не боимся и используем главное правило всей математики: “Не знаешь, что нужно, делай что можно.”
Вот и прикидываем, что в этой эпичной задачке можно сделать. Можно хотя бы расписать все данные нам члены (1-й, 7-й, 3-й, 6-й) в виде формул n-го члена, подставляя те числа, которые даны в условии.
Вот и расписываем каждый член! Прямо по формуле!
Ну, с первым членом всё и так ясно. Его вообще расписывать не надо.) Идём дальше.
Для седьмого члена мы можем записать:
a7 = a1 + (7-1)·d = a1 + 6d
Третий член:
a3 = a1 + (3-1)·d = a1 + 2d
Шестой член:
a6 = a1 + (6-1)·d = a1 + 5d
А дальше снова читаем задачку и скачиваем всю остальную полезную информацию. А именно — связь между членами.
Сумма первого и седьмого членов равна 14:
a1 + a1 + 6d = 14
2a1 + 6d = 14
Так, одно уравнение готово. Читаем дальше.)
Произведение третьего и шестого членов равно 10:
(a1 + 2d)(a1 + 5d) = 10
Получили два уравнения. Раз они относятся к одной и той же прогрессии, то должны выполняться одновременно. Объединяем наши полученные уравнения в систему:
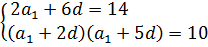
Вот и всё. Всю ценную информацию по прогрессии мы скачали и записали в виде системы уравнений. А дальше дело за алгеброй. Решение систем — уже её работа. И наша с вами, к сожалению, тоже, да…
Начнём с первого уравнения. Оно попроще будет. Выражаем из него a1. Для этого переносим 6d вправо и делим всё на двойку. Обычные тождественные преобразования, да.)
2a1 = 14 — 6d
a1 = 7 — 3d
Теперь, ясное дело, подставляем это выражение во второе уравнение:
(7 — 3d + 2d)(7 — 3d + 5d) = 10
Приводим подобные в скобках:
(7 — d)(7 + 2d) = 10
Раскрываем скобки, приводим подобные и собираем всё слева:
49 + 14d — 7d — 2d2 — 10 = 0
-2d2 + 7d + 39 = 0
Решаем это квадратное уравнение (помножив обе части на минус 1) и получаем корни:
d1 = -3
d2 = 6,5
А вот и обещанный подводный камень! Что дальше? Получилось два значения разности d! Какое из них выбрать? Тупик?
Вовсе нет! Просто ещё раз внимательно читаем условие задачи в поисках дополнительной информации! Там зачем-то употребляется слово “возрастающей”. А составители задач излишним словоблудием обычно не занимаются, да.) Вспоминаем из первого урока, что у возрастающей арифметической прогрессии разность всегда положительна.
Стало быть, из двух вариантов выбираем d = 6,5.
Так, отлично. Разность прогрессии найдена. По первому уравнению системы считаем первый член:
a1 = 7 — 3d = 7 – 3·6,5 = -3,5
Вот, практически, и всё. Что там от нас в задаче требуют? Двадцатый член? Да, пожалуйста!
a20 = a1 + (20 — 1)·d = -3,5 + 19·6,5 = 120
Ответ: 120
А теперь мы рассмотрим с вами ещё несколько коротких и простых задачек. Они, по своей сути, и вправду очень простые, но многих учеников ставят в тупик своей непривычностью и нестандартной подачей условия. Вот и пугается народ. И спотыкается на ровном месте, теряя драгоценные баллы на экзамене…
Работаем с видоизменённой формулой!
Первым делом, давайте с вами вспомним, как мы обычно задаём любую арифметическую прогрессию? Варианта два:
1) Отдельными параметрами прогрессии (скажем, a1 и d или a1 и an и т.п.);
2) В виде последовательности чисел.
Например:
(an): 1, 5, 9, 13, 17, …
К этим двум вариантам задания прогрессии мы уже попривыкли.) Но оказывается, есть ещё и третий вариант задания арифметической прогрессии! А именно – в виде формулы n-го члена. Да-да! Любую арифметическую прогрессию в общем виде можно задать формулой её n-го члена. Для каждой прогрессии — своей.)
Смотрите сами.
Пусть, например, в арифметической прогрессии a1 = 3 и d = 5. Запишем для неё формулу n-го члена:
an = 3 + 5·(n-1)
Раскрываем скобки и упрощаем:
an = -2 + 5n
Это выражение — тоже формула n-го члена! Только не общая, а уже для конкретной прогрессии. Задачки с такой видоизменённой формулой очень часто попадаются на экзамене. И частенько народ, не подумав, тут же радостно ответ пишет и… приехали.) Чем же эта формула так коварна? Здесь есть подводный камень: некоторые, глядя на формулу, сразу думают, что первый член — минус два. Хотя реально первый член — тройка…
Например, такая задачка на основе реального варианта ОГЭ:
Арифметическая прогрессия задана условием an = 5 — 1,5n. Найдите сумму первого и девятого её членов.
Здесь прогрессия задана не совсем привычно. Формула какая-то… Ничего страшного. Бывает.) Эта формула — тоже формула n-го члена арифметической прогрессии. Она тоже позволяет найти любой член прогрессии по его номеру!
Вот и ищем наши члены. Начинаем с первого члена. Тот, кто думает, что первый член — пятёрка, фатально ошибается! Потому что формула в задаче — видоизменённая. И первый член прогрессии в ней спрятан. Не беда, сейчас мы его отыщем.)
Просто берём и подставляем n=1 в формулу:
a1 = 5 — 1,5·1 = 3,5
Вот так! Первый член — три с половиной! А вовсе не пятёрка…
Подставляем теперь n=9 и считаем девятый член:
a9 = 5 — 1,5·9 = -8,5
Ну и считаем требуемую сумму:
a1 + a9 = 3,5 + (-8,5) = -5
Ответ: -5
Вот и все дела. Теперь, надеюсь, видоизменённая формула n-го члена арифметической прогрессии не поставит вас навечно в тупик.)
Работаем с рекуррентной формулой!
Рассмотрим теперь ещё один сюрприз. Частенько в задачах на арифметическую прогрессию встречается ещё одно обозначение — an+1. Это, как вы уже, наверное, догадались, “эн плюс первый” член прогрессии. Всё очень просто. Это член прогрессии, номер которого больше номера n на единичку. И всё.) Например, если в какой-нибудь задаче мы берём за an третий член, то an+1 будет четвёртым членом. И тому подобное.
Чаще всего обозначение an+1 встречается в так называемых рекуррентных формулах. Не пугаемся этого страшного слова!) Рекуррентная формула – это всего лишь способ задания любого члена арифметической прогрессии через предыдущий член. И всё.) Это ещё один, четвёртый способ задания арифметической прогрессии. Поработаем и с ним.
Допустим, арифметическая прогрессия нам задана рекуррентной формулой:
an+1 = an+4
a1 = 3
Можно посчитать второй член этой прогрессии? Легко! Если за an принять первый член прогрессии a1, то второй член будет, как раз, a1+1 = a2. Первый член нам уже дан отдельно. Это тройка. Вот и считаем по формуле:
a2 = a1 + 4 = 3+4 = 7
Третий член можно посчитать через второй:
a3 = a2 + 4 = 7+4 = 11
Четвёртый можно посчитать через третий, пятый – через четвёртый, и так далее. Продолжая эту цепочку, можно таким способом добраться до любого интересующего нас члена. А как можно посчитать сразу, скажем, 25-й член a25? К сожалению, никак… Пока предыдущий, 24-й член, не узнаем, 25-й не посчитаем. В этом и состоит принципиальное отличие рекуррентной формулы от формулы n-го члена. Рекуррентная формула работает по принципу домино, только через предыдущий член, в то время как формула n-го члена — через первый и позволяет сразу находить любой член прогрессии по его номеру. Не просчитывая всю последовательность по порядочку.)
Кстати, а как вы думаете, почему в рекуррентной формуле
an+1 = an+4
a1 = 3
первый член a1 нам задан отдельно? Ответ прост: для последовательного подсчёта членов рекуррентным способом, нам всегда необходима некая точка отсчёта. А именно — некоторый стартовый член, с которого следует начинать. Это, кстати, не обязательно может быть именно первый член. Можно начать счёт со второго члена, с третьего — с любого! С того члена, который дополнительно указан в условии в качестве стартового.
Подведём итог. Как вы видите, если число последовательно просчитываемых членов не очень большое (скажем, три или пять), то рекуррентные формулы вовсе не так уж и плохи на практике. А вот если считать предстоит много, то уже начинаются неудобства, да…
К счастью, в арифметической прогрессии рекуррентную формулу очень легко превратить в обычную. Как? Просто посчитать пару последовательных членов, вычислить разность d, найти первый член (если надо), записать формулу n-го члена в привычном виде, да и работать с ней.
В ОГЭ подобные задания частенько встречаются. Например, такая задачка:
Арифметическая прогрессия задана условиями:
an+1 = an+2,8
a2 = 3
Найдите 112-й член этой прогрессии.
Здесь прогрессия задана рекуррентным способом. Ну и ничего страшного. Любой член прогрессии можно посчитать через предыдущий. Второй член нам уже известен. Это тройка. Через него можно посчитать третий член, через третий — четвёртый и так далее вплоть до нужного нам 112-го члена. Мрачноватая перспектива, вообще-то.) А времени на экзамене немного, да…
Но! У нас же есть такой мощный инструмент, как формула n-го члена! Которая сразу выдаст нам любой член с любым номером! Вот и запустим её в дело. Для начала просто запишем в тетрадке:
an = a1 + (n-1)·d
А теперь смотрим на формулу и соображаем, какие данные у нас уже есть, а что нужно дополнительно посчитать.
Пока у нас есть только номер члена n = 112. А вот первого члена a1 и разности d — пока не хватает. Не беда, сейчас отыщем!
Читаем ещё раз задачку и видим, что:
an+1 = an+2,8 и a2 = 3
Можно посчитать третий член по известному второму? Можно!
Считаем:
a3 = a2+2,8 = 3+2,8 = 5,8
Ну вот. Теперь нам стали известны два последовательных члена прогрессии — второй и третий. Считаем разность прогрессии:
d = a3 — a2 = 5,8 — 3 = 2,8
Внимание! Ещё раз напоминаю, что разность прогрессии d — это не просто разница между двумя соседними членами! Это именно разность между членом и предыдущим членом! Стало быть, для определения разности, надо всегда от члена с большим номером отнять член с меньшим номером.
Кстати сказать, а можно ли было сразу найти разность прогрессии, не вычисляя третий член? Можно! Давайте ещё разок посмотрим на нашу рекуррентную формулу:
an+1 = an+2,8
Переводим формулу на человеческий язык: каждый член (an+1) больше предыдущего члена (an) на 2,8. Прямо по смыслу и определению арифметической прогрессии, величина 2,8 и есть разность d! Вот и всё.)
Так, разность прогрессии найдена. Осталось отыскать первый член. Не вопрос! Второй член нам уже дан по условию, а разность мы нашли только что. Вот и отнимаем разность прогрессии от второго члена:
a1 = a2 — d = 3 — 2,8 = 0,2
Вот и финишная прямая. Подставляем все чиселки в формулу n-го члена и считаем 112-й член:
a112 = a1 + (112-1)·d = 0,2 + 111·2,8 = 311
Ответ: 311
Ну как, прониклись? Мощная штука формула n-го члена, правда? Тогда решаем самостоятельно.
Для разминки:
1. Записаны первые три члена арифметической прогрессии:
20; 17; 14; …
Какое число стоит в этой арифметической прогрессии на 91-м месте?
2. В третьем ряду киноконцертного зала 34 места, а в пятнадцатом — 58 мест. Сколько мест в одиннадцатом ряду, если считать число мест в каждом ряду арифметической прогрессией?
Эта чуть покруче будет:
3. Дана арифметическая прогрессия:
32; 31,6; 31,2; …
Найдите номер первого отрицательного члена этой прогрессии.
Картинку рисовать муторно, да. Слишком уж медленно наша прогрессия к отрицательным числам приближается… Но вы же формулу n-го члена знаете! Вперёд! Ну, и элемент творчества небольшой надо проявить, да.)
А вот это уже не разминка:
3. Известно, что в арифметической прогрессии a6 = 6 и a251 = -190. Найдите a101.
4. Третий член арифметической прогрессии в три раза меньше шестого, а сумма второго и пятого членов равна 16. Найдите пятнадцатый член этой прогрессии.
5. Сумма восьмого и четырнадцатого членов убывающей арифметической прогрессии равна нулю, а произведение третьего и двенадцатого членов равно -32. Найдите девятнадцатый член прогрессии.
Задачки попроще, для отдыха:
6. Арифметическая прогрессия задана условием: an = -0,6+8,6n. Найдите произведение первого и шестнадцатого её членов.
7. Арифметическая прогрессия задана условиями:
an+1 = an — 0,3
a1 = 10
Найдите 51-й член прогрессии.
Ответы (в беспорядке): 54; -5; 82; -70; -250; 1096; -16; 50;
Ну вот и второй этап знакомства с арифметической прогрессией успешно пройден! Осталось ещё научиться быстро складывать её члены. Такие задачки тоже часто встречаются! Об этом — в следующем уроке.
