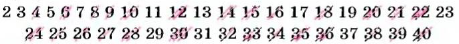Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given a number N, find the smallest prime divisor of N.
Examples:
Input: 25
Output: 5Input: 31
Output: 31
Approach:
- Check if the number is divisible by 2 or not.
- Iterate from i = 3 to sqrt(N) and making a jump of 2.
- If any of the numbers divide N then it is the smallest prime divisor.
- If none of them divide, then N is the answer.
Below is the implementation of the above algorithm:
C++
#include <bits/stdc++.h>
using namespace std;
int smallestDivisor(int n)
{
if (n % 2 == 0)
return 2;
for (int i = 3; i * i <= n; i += 2) {
if (n % i == 0)
return i;
}
return n;
}
int main()
{
int n = 31;
cout << smallestDivisor(n);
return 0;
}
Java
import java.io.*;
class GFG {
static int smallestDivisor(int n)
{
if (n % 2 == 0)
return 2;
for (int i = 3; i * i <= n; i += 2) {
if (n % i == 0)
return i;
}
return n;
}
public static void main (String[] args) {
int n = 31;
System.out.println (smallestDivisor(n));
}
}
Python3
def smallestDivisor(n):
if (n % 2 == 0):
return 2;
i = 3;
while(i * i <= n):
if (n % i == 0):
return i;
i += 2;
return n;
n = 31;
print(smallestDivisor(n));
C#
using System;
class GFG
{
static int smallestDivisor(int n)
{
if (n % 2 == 0)
return 2;
for (int i = 3;
i * i <= n; i += 2)
{
if (n % i == 0)
return i;
}
return n;
}
static public void Main ()
{
int n = 31;
Console.WriteLine(smallestDivisor(n));
}
}
PHP
<?php
function smallestDivisor($n)
{
if ($n % 2 == 0)
return 2;
for ($i = 3; $i * $i <= $n; $i += 2)
{
if ($n % $i == 0)
return $i;
}
return $n;
}
$n = 31;
echo smallestDivisor($n);
?>
Javascript
<script>
function smallestDivisor(n) {
if (n % 2 == 0)
return 2;
for (var i = 3; i * i <= n; i += 2) {
if (n % i == 0)
return i;
}
return n;
}
var n = 31;
document.write(smallestDivisor(n));
</script>
Time Complexity: O(sqrt(N)), as we are using a loop to traverse sqrt (N) times. As the condition is i*i<=N, on application of sqrt function on both the sides we get sqrt (i*i) <= sqrt(N), which is i<= sqrt(N), therefore the loop will traverse for sqrt(N) times.
Auxiliary Space: O(1), as we are not using any extra space.
Last Updated :
13 Jun, 2022
Like Article
Save Article
В данной статье мы поговорим о том, как найти все делители числа. Начнем с доказательства теоремы, с помощью которой можно задать вид всех делителей определенного числа. Далее возьмем примеры нахождения всех нужных делителей и покажем, как именно определить, сколько делителей имеет конкретное число. В последнем пункте подробно рассмотрим примеры задач на нахождение общих делителей нескольких чисел.
Как найти все делители числа
Чтобы понять материал, изложенный в данном пункте, нужно хорошо знать, что вообще из себя представляют кратные числа и делители. Здесь мы поговорим только о поиске делителей натуральных чисел, т.е. целых положительных. Этим можно ограничиться, поскольку свойство делимости гласит, что делители целого отрицательного числа аналогичны делителям целого положительного, которое будет противоположным по отношению к этому числу. Также сразу уточним, что у нуля есть бесконечно большое число делителей, и находить их смысла не имеет, поскольку в итоге все равно получится 0.
Если речь идет о простом числе, то его можно разделить только на единицу и на само себя. Значит, у любого простого числа a есть всего 4 делителя, два из которых больше 0 и два меньше: 1, -1, a, -a. Возьмем простое число 7: у него есть делители 7, -7, 1 и -1, и все. Еще один пример: 367 – тоже простое число, которое можно разделить лишь на 1, -1, 367 и -367.
Сложнее определить все делители составного числа. Сформулируем теорему, которая лежит в основе данного действия.
Допустим, у нас есть выражение, означающее каноническое разложение числа на простые множители, вида a=p1s1·p2s2·…·pnsn. Тогда натуральными делителями числа a будут следующие числа: d=p1t2·p2t2·…·pntn, где t1=0, 1, …, s1, t2=0, 1, …, s2, …, tn=0, 1, …, sn.
Перейдем к доказательству этой теоремы. Зная основное определение делимости, мы можем утверждать, что a можно разделить на d, если есть такое число q, что делает верным равенство a=d·q, т.е. q=p1(s1−t1)·p2(s2-t2)·…·pn(sn-tn).
Любое число, делящее a, будет иметь именно такой вид, поскольку, согласно свойствам делимости, других простых множителей, кроме p1, p2, …, pn, оно иметь не может, а их показатели в данном случае не превысят s1, s2, …, sn.
Учитывая доказательство этой теоремы, мы можем сформировать схему нахождения всех положительных делителей данного числа.
Для этого нужно выполнить следующие действия:
- Выполнить каноническое разложение на простые множители и получить выражение вида a=p1s1·p2s2·…·pnsn.
- Найти все значения d=p1t2·p2t2·…·pntn, где числа t1, t2, …, tn будут принимать независимо друг от друга каждое из значений t1=0, 1, …, s1, t2=0, 1, …, s2, …, tn=0, 1, …, sn.
Самым трудным в таком расчете является именно перебор всех комбинаций указанных значений. Разберем подробно решения нескольких задач, чтобы наглядно показать применение данной схемы на практике.
Условие: найти все делители 8.
Решение
Разложим восьмерку на простые множители и получим 8=2·2·2. Переведем разложение в каноническую форму и получим 8=23. Следовательно, a=8, p1=2, s1=3.
Поскольку все делители восьмерки будут значениями p1t1=2t1, то t1 может принять значения нуля, единицы, двойки, тройки. 3 будет последним значением, ведь s1=3. Таким образом, если t1=0, то 2t1=20=1, если 1, то 2t1=21=2, если 2, то 2t1=22=4, а если 3, то 2t1=23=8.
Для нахождения делителей удобно все полученные значения оформлять в виде таблицы:
| t1 | 2t1 |
| 0 | 20=1 |
| 1 | 21=2 |
| 2 | 22=4 |
| 3 | 23=8 |
Значит, положительными делителями восьмерки будут числа 1, 2, 4 и 8, а отрицательными −1, −2, −4 и −8.
Ответ: делителями данного числа будут ±1, ±2, ±4, ±8.
Возьмем пример чуть сложнее: в нем при разложении числа получится не один, а два множителя.
Условие: найдите все делители числа 567, являющиеся натуральными числами.
Решение
Начнем с разложения данного числа на простые множители.
56718963217133337
Приведем разложение к каноническому виду и получим 567=34·7. Затем перейдем к вычислению всех натуральных множителей. Для этого будем присваивать t1 и t2 значения 0, 1, 2, 3, 4 и 0, 1, вычисляя при этом значения 3t1·7t2. Результаты будем вносить в таблицу:
| t1 | t2 | 3t1·7t2 |
| 0 | 0 | 30·70=1 |
| 0 | 1 | 30·71=7 |
| 1 | 0 | 31·70=3 |
| 1 | 1 | 31·71=21 |
| 2 | 0 | 32·70=9 |
| 2 | 1 | 32·71=63 |
| 3 | 0 | 33·70=27 |
| 3 | 1 | 33·71=189 |
| 4 | 0 | 34·70=81 |
| 4 | 1 | 34·71=567 |
Ответ: натуральными делителями 567 будут числа 27, 63, 81, 189, 1, 3, 7, 9, 21 и 567.
Продолжим усложнять наши примеры – возьмем четырехзначное число.
Условие: найти все делители 3 900, которые будут больше 0.
Решение
Проводим разложение данного числа на простые множители. В каноническом виде оно будет выглядеть как 3 900=22·3·52·13. Теперь приступаем к нахождению положительных делителей, подставляя в выражение 2t1·3t2·5t3·13t4 значения t1, равные 0, 1 и 2, t2=0,1, t3=0, 1, 2, t4=0, 1. Результаты представляем в табличном виде:
| t1 | t2 | t3 | t4 | 2t1·3t2·5t3·13t4 |
| 0 | 0 | 0 | 0 | 20·30·50·130=1 |
| 0 | 0 | 0 | 1 | 20·30·50·131=13 |
| 0 | 0 | 1 | 0 | 20·30·51·130=5 |
| 0 | 0 | 1 | 1 | 20·30·51·131=65 |
| 0 | 0 | 2 | 0 | 20·30·52·130=25 |
| 0 | 0 | 2 | 1 | 20·30·52·131=325 |
| 0 | 1 | 0 | 0 | 20·31·50·130=3 |
| 0 | 1 | 0 | 1 | 20·31·50·131=39 |
| 0 | 1 | 1 | 0 | 20·31·51·130=15 |
| 0 | 1 | 1 | 1 | 20·31·51·131=195 |
| 0 | 1 | 2 | 0 | 20·31·52·130=75 |
| 0 | 1 | 2 | 1 | 20·31·52·131=975 |
| t1 | t2 | t3 | t4 | 2t1·3t2·5t3·13t4 |
| 1 | 0 | 0 | 0 | 21·30·50·130=2 |
| 1 | 0 | 0 | 1 | 21·30·50·131=26 |
| 1 | 0 | 1 | 0 | 21·30·51·130=10 |
| 1 | 0 | 1 | 1 | 21·30·51·131=130 |
| 1 | 0 | 2 | 0 | 21·30·52·130=50 |
| 1 | 0 | 2 | 1 | 21·30·52·131=650 |
| 1 | 1 | 0 | 0 | 21·31·50·130=6 |
| 1 | 1 | 0 | 1 | 21·31·50·131=78 |
| 1 | 1 | 1 | 0 | 21·31·51·130=30 |
| 1 | 1 | 1 | 1 | 21·31·51·131=390 |
| 1 | 1 | 2 | 0 | 21·31·52·130=150 |
| 1 | 1 | 2 | 1 | 21·31·52·131=1950 |
| t1 | t2 | t3 | t4 | 2t1·3t2·5t3·13t4 |
| 2 | 0 | 0 | 0 | 22·30·50·130=4 |
| 2 | 0 | 0 | 1 | 22·30·50·131=52 |
| 2 | 0 | 1 | 0 | 22·30·51·130=20 |
| 2 | 0 | 1 | 1 | 22·30·51·131=260 |
| 2 | 0 | 2 | 0 | 22·30·52·130=100 |
| 2 | 1 | 0 | 1 | 22·30·52·131=1300 |
| 2 | 1 | 0 | 0 | 22·31·50·130=12 |
| 2 | 1 | 0 | 1 | 22·31·50·131=156 |
| 2 | 1 | 1 | 0 | 22·31·51·130=60 |
| 2 | 1 | 1 | 1 | 22·31·51·131=780 |
| 2 | 1 | 2 | 0 | 22·31·52·130=300 |
| 2 | 1 | 2 | 1 | 22·31·52·131=3900 |
Ответ: делителями числа 3 900 будут:195, 260, 300, 325, 390, 650, 780, 975, 75, 78, 100, 130, 150, 156, 13,15, 20, 25, 26, 30, 39, 50,52, 60, 65, 1, 2, 3, 4, 5, 6, 10, 12, 1 300, 1 950, 3 900
Как определить количество делителей конкретного числа
Чтобы узнать, сколько положительных делителей у конкретного числа a, каноническое разложение которого выглядит как a=p1s1·p2s2·…·pnsn, нужно найти значение выражения (s1+1) ·(s2+1) ·…·(sn+1). О количестве наборов переменных t1, t2, …, tn мы можем судить по величине записанного выражения.
Покажем на примере, как это вычисляется. Определим, сколько будет натуральных делителей у числа 3 900, которое мы использовали в предыдущей задаче. Каноническое разложение мы уже записывали: 3 900=22·3·52·13. Значит, s1=2, s2=1, s3=2, s4=1. Теперь подставим значения s1, s2, s3 и s4 в выражение (s1+1) ·(s2+1) ·(s3+1) ·(s4+1) и вычислим его значение. Имеем (2+1)·(1+1)·(2+1)·(1+1)=3·2·3·2=36. Значит, это число имеет всего 36 делителей, являющихся натуральными числами. Пересчитаем то количество, что у нас получилось в предыдущей задаче, и убедимся в правильности решения. Если учесть и отрицательные делители, которых столько же, сколько и положительных, то получится, что у данного числа всего будет 72 делителя.
Условие: определите, сколько делителей имеет 84.
Решение
Раскладываем число на множители.
844221712237
Записываем каноническое разложение: 84=22·3·7. Определяем, сколько у нас получится положительных делителей: (2+1)·(1+1)·(1+1) =12. Для учета отрицательных нужно умножить это число на 2:2·12=24.
Ответ: всего у 84 будет 24 делителя – 12 положительных и 12 отрицательных.
Как вычислить общие делители нескольких чисел
Зная свойства наибольшего общего делителя, можно утверждать, что количество делителей некоторого набора целых чисел будет совпадать с количеством делителей НОД тех же чисел. Это будет справедливо не только для двух чисел, но и для большего их количества. Следовательно, чтобы вычислить все общие делители нескольких чисел, надо определить их наибольший общий множитель и найти все его делители.
Разберем пару таких задач.
Условие: сколько будет натуральных общих делителей у чисел 140 и 50? Вычислите их все.
Решение
Начнем с вычисления НОД (140, 50).
Для этого нам потребуется алгоритм Евклида:
140=50·2+40, 50=40·1+10, 40=10·4, значит, НОД (50, 140)=10.
Далее выясним, сколько положительных делителей есть у десяти. Разложим его на простые множители и получим 20·50=1, 20·51=5, 21·50=2 и 21·51=10. Значит, все натуральные общие делители исходного числа – это 1, 2, 5 и 10, а всего их четыре.
Ответ: данные числа имеют четыре натуральных делителя, равные 10, 5, 2 и 1.
Условие: выясните, сколько общих положительных делителей есть у чисел 585, 315, 90 и 45.
Решение
Вычислим их наибольший общий делитель, разложив число на простые множители. Поскольку 90=2·3·3·5, 45=3·3·5, 315=3·3·5·7 и 585=3·3·5·13, то таким делителем будет 5: НОД (90, 45, 315, 585) =3·3·5=32·5.
Чтобы узнать количество этих чисел, нужно выяснить, сколько положительных делителей имеет НОД.
Считаем:
НОД (90, 45, 315, 585) =32·5:(2+1)·(1+1) =6.
Ответ: у данных чисел шесть общих делителей.
Делимость
До того как начать разбирать эти две аббревиатуры, рассмотрим сначала понятие делимости. Что значит фраза “число А делится на число Б”? Например, 24 делится на 6. И что значит “не делится”? Например, 27 не делится на 2.
Когда мы говорим о делимости, то речь идет о целочисленном делении целых чисел. И делимость означает, что число делится на делитель нацело, без остатка.
24 делится на 6, частное равно 4, а остаток нулю.
27 не делится на 2, частное равно 13, а остаток равен одному.
Признаки делимости
Проверить, делится ли одно число на заданное, можно просто выполнив деление. Но если число большое, а результат самого деления нам не так чтобы нужен? Можно ли не находя частное, определить, делится ли число?
Существуют несколько признаков делимости, когда по внешнему вида числа мы можем определить, делится ли оно на заданное. Рассмотрим только некоторые из них, те, которые легко проверяются.
По последней цифре
Число делится на 2, если его последняя цифра – четная.
Число делится на 5, если его последняя цифра – 5 или 0.
Число делится на 10, если его последняя цифра – 0.
Например, 234 делится на 2, так как 4 – четная.
235 делится на 5, так как последняя цифра – 5.
190 делится на 10 и на 5, так как последняя цифра – 0.
По сумме цифр числа
Число делится на 3, если сумма цифр этого числа делится на 3.
Число делится на 9, если сумма цифр этого числа делится на 9.
Например, 393 делится на 3, так как сумма цифр этого числа 3+9+3=15 делится на 3.
180 делится на 9, так как сумма цифр этого числа 1+8+0=9 делится на 9.
Число делится на 6, если оно делится на 2 и на 3 одновременно.
Например, 36 делится на 2 (6 четная) и на 3 (3+6=9 – делится на 3), поэтому оно делится на 6.
Простые и составные числа
Среди натуральных чисел выделяют такие числа, которые делятся только на 1 и на самого себя. Такие числа называются простыми. Остальные числа, имеющие больше двух делителей, называют составными. Отдельно выделяют 1, у нее только один делитель.
Пример простого числа – 2, 3, 5, 7, 11, 13, 17, 19 и так далее. Существуют специальные таблицы простых чисел, но многие проблемы простых чисел до сих пор не решены.
Разложение на простые множители
Для составных чисел можно найти такие множители, которые будут только простыми числами, а произведение этих множителей будет равно исходному числу.
Например, 24=2*2*2*3.
Это произведение и называется разложением на простые множители. Если множители отсортированы по возрастанию, то для каждого конкретного числа это разложение будет единственным.
Для построения такого разложения существует четкий алгоритм.
- Записываем в левый столбец исходное число, проводим вертикальную черту, отделяя правый столбец.
- Проверяем, делится ли число на 2. Если да, то записываем 2 в правый столбец, в левый столбец в следующей строке записываем кратное исходного числа и 2.
- Проверяем, делится ли полученное число на 2, если да, то действуем как в пункте 2.
- Если нет, то проверяем, делится ли наше число на 3. Если да, то 3 записываем в правый столбец, а в левый столбец строчкой ниже пишем кратное от деления на 3 и переходим к пункту 3.
- Если число не делится на 3, то переходим к следующему числу в списке простых чисел – 5.
- Каждый раз начинаем проверку делимости с 2, постепенно переходя к все большим и большим простым числам, если это необходимо.
- Так действуем до тех пор, пока число в левом столбце не станет равно 1. Тогда останавливаемся.
- В правом столбце у нас записаны все простые множители числа.
Наибольший общий делитель
НОД или наибольший общий делитель для нескольких чисел – это такое наибольшее число, на которое делятся все эти числа.
Например, НОД(12, 18)=6.
Зная разложение чисел на простые множители, легко найти их НОД. Выписываем совпадающие множители, их произведение и даст нам НОД.
Наименьшее общее кратное
НОК или наименьшее общее кратное нескольких чисел – это такое наименьшее число, которое делится на все эти числа.
Например, НОК(4, 6)=12.
Зная разложение чисел на простые множители, легко найти их НОК. К множителям меньшего числа дописываем несовпадающие множители. Это произведение и даст нам НОК.
Взаимно простые числа
Если у двух составных чисел нет общих простых множителей, то такие числа называются взаимно простыми. НОК таких чисел равен их произведению, а НОД равен 1.
Содержание:
Делимость натуральных чисел
Делители и кратные натурального числа. простые числа
Посмотрите на рисунок 1. Вы видите, что 6 яблок разделили на 2 кучки по 3 яблока в каждой. Тут число 6 является делимым, число 2 — делителем, а число 3 — частным. Однако 6 яблок можно разделить и иначе — разложить их на 3 кучки по 2 яблока в каждой. Тогда для делимого 6 число 3 является делителем, а число 2 — частным. Это значит, что числа 2 и 3 являются делителями числа 6. В то же время число 6 является кратным для каждого из своих делителей — и для числа 2, и для числа 3. Делители и кратные являются натуральными числами.
Определение:
Делителем числа называется такое число, на которое делится данное число.
Kpaтным числа называется такое число, которое делится на данное число.
Пример:
Есть ли другие делители у числа 6? Да. Число 6 делится ещё на 1 и само на себя. Значит, всего у числа 6 есть четыре делителя: 1; 2;3;6.
Обратите внимание:
каждое натуральное число, начиная с числа 2. имеет по меньшей мере два делителя — число 1 и само это число. Другие делители находят по специальным правилам.
Пример:
Найдите все делители числа: 1) 7; 2) 12; 3)25.
Решение:
1) У числа 7 есть по меньшей мере два делителя — 1 и 7. Ни на одно другое натуральное число 7 не делится, поэтому у него всего два делителя: 1 и 7.
2) Число 12 имеет по меньшей мере два делителя — 1 и 2. Далее последовательно проверяем делимость числа 12 на натуральные числа от 2 до 11.
3) У числа 25 есть как минимум два делителя: 1 и 25 На 2, 3 и 4, а также на числа от 6 до 24 это число не делится. 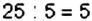
Запомните: Натуральное число, у которого есть только два делителя (1 и само число), называется простым. Натуральное число, у которого больше двух делителей, называется составным.
Например, 7 — простое число, а 12 и 25 — составные.
Пример:
Является ли 1 простым числом? А составным? Нет, поскольку у числа 1 только один делитель. Значит, число 1 особенное. Оно и не простое, и не составное.
Обратите внимание:
наименьшим простым числом является число 2.
Чтобы выписать некоторое количество простых чисел, можно воспользоваться способом, придуманным ещё в III в до н.э. Эратосфеном Киренским (27бг. до н. э. — 194 г. до н. э ). греческим математиком, астрономом, географом и поэтом. В честь учёного этот способ называется «решето Эратосфена». На рисунке (с. 4) вы видите, как находили простые числа от 2 до 50. Попробуйте самостоятельно объяснить, как это делали.
Признаки делимости на 2, 10, 5
Запишем натуральный ряд чисел:
1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12…
Умножим каждое число на 2. Получили ряд чисел, кратных числу 2:
2; 4; 6; 8; 10; 12; 14; 16; 18; 20; 22; 24…
Такие числа называют чётными. Их можно задать формулой:
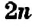
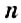
В натуральном ряде чётные числа чередуются с нечётными числами — они не делятся на 2. Например, числа 3, 5, 11 — нечётные. Их также можно задать формулой:
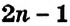
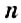
Пример:
Как выяснить, является ли чётным данное число? Для этого пользуются признаком делимости на 2.
Признак делимости на 2
На 2 делятся те и только те числа, запись которых заканчивается чётной цифрой.
Например, запись числа 538 заканчивается цифрой 8, которая является чётной, поэтому число 538 делится на 2. Действительно, 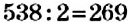
Опираясь на натуральный ряд чисел, запишем ряд чисел, кратных числу 10:
Как видим, запись каждого числа этого ряда заканчивается цифрой 0. Именно в этом и состоит признак делимости на 10.
Признак делимости на 10
На 10 делятся те и только те числа, запись которых заканчивается цифрой 0.
Например, число 1000 делится на 10, а число 1001 не делится.
Пример:
Можно ли считать признак делимости на 10 признаком делимости на 5? Нет, так как существуют числа, которые делятся на 5, но не делятся на 10. Например, число 2055.
Опираясь на натуральный ряд чисел, запишем ряд чисел, кратных числу 5:
Как видим, запись каждого числа этого ряда заканчивается либо цифрой 5, либо цифрой 0. Именно в этом и состоит признак делимости на 5.
Признак делимости на 5
На 5 делятся те и только те числа, запись которых заканчивается либо цифрой 5, либо цифрой 0.
Например, число 85 делится на 5, а число 86 – не делится.
Пример:
Найдите все нечётные числа от 10 до 40, которые делятся на 5.
Решение:
Способ 1. Сначала выберем все нечётные числа от 10 до 40:
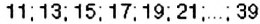
Применив к этим числам признак делимости на 5, получим искомые числа: 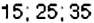
Способ 2. Искомые числа — нечётные и делятся на 5. Поэтому : среди них не должно быть чисел, запись которых заканчивается цифрой 0. поскольку такие числа — чётные. Итак, среди чисел от : 10 до 40 достаточно выбрать числа, запись которых заканчивается только цифрой 5. Отсюда искомым и будут числа: 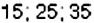
Обратите внимание:
среди чисел, делящихся на 5. чётные числа делятся и на 10. а нечётные — нет.
Признак делимости на 4. Число делится на 4 тогда и только тогда, когда на 4 делится число, образованное двумя последними цифрами данного числа. Например, число 3436 делится на 4, поскольку число 36 делится на 4.
Признак делимости на 8. Число делится на 8 тогда и только тогда, когда на 8 делится число, образованное тремя последними цифрами данного числа. Например, число 29176 делится на 8, поскольку число 176 делится на 8.
Признак делимости на 25. Число делится на 25 тогда и только тогда, когда на 25 делится число, образованное двумя последними цифрами данного числа Например, число 6575 делится на 25, поскольку число 75 делится на 25.
Признак делимости на 125. Число делится на 125 тогда и только тогда, когда на 125 делится число, образованное тремя последними цифрами данного числа. Например, число 36 375 делится на 125, поскольку число 375 делится на 125.
Признаки делимости на 9, 3
Запишем ряд чисел, кратных числу 9:
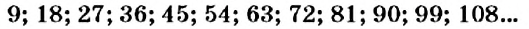
Как видим, признак делимости на 9 не связан с последней цифрой в записи числа. Он связан с сумой цифр в этой записи. Позже вы сможете это обосновать.
Признак делимости на 9
На 9 делятся те и только те числа, сумма цифр которых делится на 9.
Например, число 1476 делится на 9, поскольку 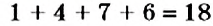
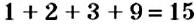
Пример:
Как выяснить, делится ли число на 3? Для этого пользуются признаком делимости на 3.
Признак делимости на 3
На 3 делятся те и только те числа, сумма цифр которых делится на 3.
Например, в числе 237 сумма цифр равна: 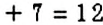
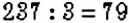
Пример:
Можно ли считать, что числа, которые делятся на 9, делятся и на 3? Да. Поскольку сумма цифр чисел, кратных числу 9, делится на 9, то она делится и на 3. Однако обратное утверждение не будет верным: числа, которые делятся на 3, не всегда делятся на 9. Например, числа 12, 33, 213 делятся на 3, но не делятся на 9.
Пример:
Найдите все трёхзначные числа, которые содержат цифры 5 и 1 и делятся на 9.
Решение:
Обозначим неизвестную цифру звездочкой. Сумма цифр искомого числа равна: 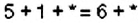
У вас мог возникнуть вопрос: «Как объяснить, почему сумма цифр в записи числа может показывать, делится ли число на 9?» Разберёмся на примерах.
Числа 99 и 999 делятся на 9, а числа 100 и 1000 на 9 не делятся. Представим эти числа в виде сумм:
Проанализируем полученные суммы. В столбике слева каждое слагаемое суммы делится на 9, а в столбике справа — нет. Вообще, если каждое слагаемое делится на данное число, то их сумма делится на данное число; если одно из слагаемых не делится на данное число, а сумма всех остальных слагаемых делится на данное число, то сумма не делится на данное число. Запишем число 351 в виде суммы разрядных слагаемых и преобразуем её:
В полученной сумме каждое слагаемое делится на 9, поэтому число 351 делится на 9. Как видим, результат зависит от последнего слагаемого, которое получили как сумму: 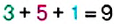
Разложение чисел на множители. Наибольший общий делитель
Вы знаете, что каждое натуральное число, большее 1, имеет несколько делителей, поэтому его можно представить в виде произведения своих делителей. Например: 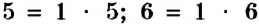
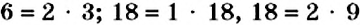
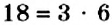
Число 5 — простое. Его можно разложить на множители только одним способом. Числа 6 и 18 — составные. Для них существует два и более разложений на множители. Однако эти разложения отличаются. В разложении 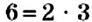
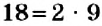
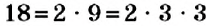
Определение:
Разложение числа на множители, в котором все множители — простые числа, называется разложением числа на простые множители.
Пример:
Является ли разложением на простые множители равенство 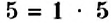
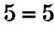
Пример:
Разложите на простые множители число 210.
Решение:
С помощью разложения числа на простые множители ищут общие делители двух чисел. Например, у чисел 12 и 30 есть два простых общих делителя — числа 2 и 3. Но числа 12 и 30 делятся и на число 6, то есть на произведение своих общих делителей. Число 6 — наибольшее число, на которое одновременно делится и число 12, и число 30. Такое число называют наибольшим общим делителем двух чисел 12 и 30.

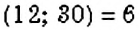
Пример:
Найдите НОД чисел 18 и 45.
Решение:
Определение:
Наибольшим общим делителем двух чисел называется наибольшее число, на которое делится каждое из данных чисел.
Правило нахождения НОД
Чтобы найти НОД двух чисел:
1) разложите данные числа на простые множители;
2) найдите произведение общих делителей данных чисел.
Пример:
Можно ли найти НОД двух чисел, не имеющих общих делителей, кроме числа 1? Да. Но НОД таких чисел равен 1.
Два числа, НОД которых равен 1, называют взаимно простыми. Например, 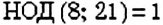
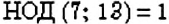
Пример:
Можно ли найти НОД нескольких чисел? Да. Для этого выполняют те же действия, что и в задаче 3, но для нескольких чисел. Например, найдём 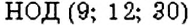
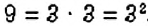
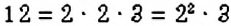
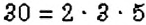
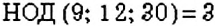
Интересный способ нахождения НОД двух чисел описал Евклид (около 365 – 300 лет до н. э.) в своей книге «Начала». В честь учёного этот способ называется «алгоритмом Евклида». Пусть нужно найти НОД двух чисел 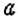
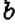
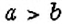
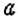
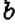
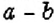
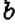
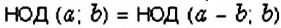
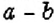
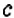
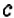
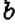
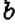
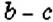
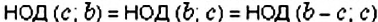
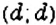
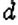
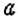
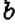
Например,
Наименьшее общее кратное
Найдём кратные числа 4. Для этого достаточно умножить число 4 на числа натурального ряда:
Аналогично найдём кратные числа 6:
Среди кратных числа 4 и числа 6 есть такие числа, которые делятся на оба данных числа:
Эти числа являются общими кратными чисел 4 и 6. Наименьшим среди них является число 12. Это — наименьшее общее кратное двух чисел 4 и 6.
Записывают: 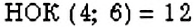
Определение:
Наименьшим общим кратным двух чисел называется наименьшее число, которое делится на каждое из данных чисел.
Общие кратные нескольких чисел можно находить при помощи разложений данных чисел на простые множители.
Пример:
Найдите НОК чисел 18 и 45.
Решение:
Правило находжения НОК
Чтобы найти НОК двух чисел:
- разложите данные числа на простые множители;
- запишите разложение одного из данных чисел;
- допишите к этому разложению такие множители из разложения другого числа, которые ещё не вошли в произведение;
- вычислите полученное произведение.
Пример:
Как найти НОК двух взаимно простых чисел? Нескольких чисел?
Поскольку у взаимно простых чисел нет других общих делителей, кроме 1, то НОК взаимно простых чисел равно их произведению. Например,
НОК нескольких чисел находят так же, как и двух чисел. Например, найдём 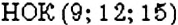
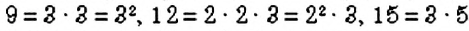
Оказывается, между НОК и НОД чисел 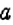
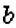
Например, для чисел 54 и 48 получим:
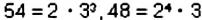
Отсюда 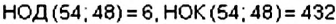
——–
Делимость натуральных чисел
В этом разделе рассматриваются важнейшие сведения из теории чисел. Это очень древняя и интересная математическая наука, которая исследует свойства натуральных чисел, связанные с их делением. Кратко основное содержание раздела выглядит так.
- Деление и делители числа.
- Признаки делимости на 10, 5 и 2.
- Признаки делимости на 3 и 9.
- Разложение чисел на простые множители.
- Наибольший общий делитель.
- Наименьшее общее кратное.
Эти темы часто используются в последующих разделах математики. В частности, без их знания невозможно успешно изучать обыкновенные дроби. Поэтому раздел 1 учебника можно считать введением к разделу 2.
Деление и делители числа
Складывать и умножать можно любые числа. Вычитание возможно лишь тогда, когда вычитаемое не больше уменьшаемого. Сложнее с делением. Деление – это действие, обратное умножению.
20 : 4 = 5, потому что 5*4 = 20.
Разделить одно число на другое — значит найти такое третье число, которое при умножении на второе дает первое число. То есть, если 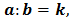
Вы уже знаете, что иногда при делении одного числа на другое получают неполное частное и остаток. Вы также знаете, что делить можно и дробные числа. В этом разделе мы будем рассматривать деление только натуральных чисел, причем без остатка.
Например, число 21 делится на 7. Говорят, что число 7 является делителем числа 21. Делителями числа 21 являются также числа 1, 3 и 21. Никакое другое число не является делителем числа 21.
Если 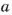
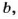
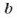
Например, число 22 имеет четыре делителя: 1,2,11 и 22;
- число 9 имеет три делителя: 1, 3 и 9;
- число 7 имеет два делителя: 1 и 7.
Число, которое имеет только два делителя, называется простым числом. Можно сказать и так. Число, которое делится только на 1 и само на себя, называется простым.
Простыми являются числа 2, 3, 5, 7, 11, 13, 17, 19, … . Простых чисел существует бесконечно много. Таблица простых чисел, меньших 1000, представлена на форзаце учебника.
Число, имеющее больше двух делителей, называется составным.
Простое 7 = 1-7.
Составное 14=1-2-7.
1 — не простое и не составное.
Составными, например, являются числа 4, (5, 8, 9, 10, 12, 14. Составных чисел также бесконечно много.
Число 1 имеет только один делитель: 1. Его не принято называть ни простым, ни составным числом.
В зависимости от количества делителей все натуральные числа делятся на три класса: простые числа, составные числа, число 1.
Если простые числа записать в порядке их возрастания, то образуется последовательность простых чисел:
2,3, 5, 7, 11, 13, 17…..
Последовательность простых чисел имеет много интересных свойств и тайн. Например, еще ученые Древней Греции заметили, что среди простых чисел много таких, разность которых равна 2, например: 3 и 5, 5 и 7, 11 и 13, 17 и 10 и т. д. Такие пары чисел называются простыми числами близнецами.
Уже более 25 веков математики пытаются выяснить, существуют ли наибольшие числа-близнецы, но и до сих пор ответа на этот вопрос мы не знаем.
Существует также много других проблем (еще не решенных задач), связанных с простыми числами.
Выполнение заданий:
Пример №1
Проверьте, является ли число 7 делителем числа 63. А числа 67?
Решение:
63 : 7 = 9, поэтому число 7 – делитель 63.
67:7 = 9 (остаток 4), поэтому 7 – не делитель числа 67.
Пример №2
Найдите наибольший делитель и наибольший простой делитель числа 20.
Решение:
Делителями числа 20 являются 1, 2, 4, 5, 10, 20. Наибольший из них – 20, наибольший простой делитель – 5.
Признаки делимости на 10, 5 и 2
Как узнать, делится ли то или иное число на 10? Очень легко. Нужно лишь посмотреть на его последнюю цифру. Если она 0, то данное число делится на 10. Если же последняя цифра не 0, то это число на 10 не делится. Два последние предложения можно заменить одним, которое называется признаком делимости чисел на 10.
На 10 делятся все те и только те числа, которые оканчиваются цифрой 0.
Используя этот признак, можно сразу (не выполняя деления) сказать, что числа 130, 3700, 4080 делятся на 10, а числа 83, 305, 1001 на 10 не делятся.
Признак делимости на 5 можно сформулировать так.
На 5 делятся все те и только те числа, которые оканчиваются цифрой 5 или 0.
Например, каждое из чисел 95, 375, 70, 4900 делится на 5, а каждою из чисел 37, 559, 5008 на 5 не делится. Убедитесь в этом, разделив каждое из этих чисел на 5.
На 2 делится каждое натуральное число, которое оканчивается цифрой 0, 2, 4, 6 или 8. Эти цифры называют четными. Поэтому признак делимости на 2 можно сформулировать так.
На 2 делятся все те и только те числа, которые оканчиваются четной цифрой.
Примеры чисел, которые делятся на 2:
0, 2, 4, 6, 8, 10, 12, 14, 16, 376, 11 108.
Числа, которые делятся на 2, называются четными.
Цифры 1, 3, 5, 7, 9 называются нечетными. Каждое натуральное число, которое оканчивается нечетной цифрой, – нечетное. Нечетное число не делится на 2. В зависимости отделимости на 2 все натуральные числа можно разбить на два класса: четные и нечетные числа.
11а координатном луче за каждым четным числом следует нечетное, а за каждым нечетным – четное (рис. 2).
Выполнение заданий:
Пример №3
Найдите наибольшее четное трехзначное число.
Решение:
Наибольшее трехзначное число 999 – нечетное. Ему предшествует четное число 998. Следовательно, наибольшее четное трехзначное число 998.
Пример №4
Сколько существует нечетных чисел, которые больше 90 и меньше 100?
Решение:
Такими являются числа 91,93, 95, 97 и 99. Их всего 5.
Пример №5
Докажите, что сумма двух нечетных чисел – число четное.
Решение:
Если числа 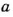
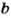
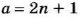
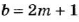
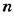
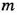
Тогда 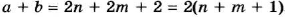
Признаки делимости на 3 и 9
Чтобы узнать, делится число на 3 или нет, находят его сумму цифр. Например, сумма цифр числа 21 204 равна 9, поскольку 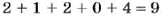
На 3 делятся все те и только те числа, сумма цифр которых делится на 3.
Примеры: Сумма цифр числа 31 104 равна 9, а 9 делится на 3, поэтому и число 31 104 делится на 3. Сумма цифр числа 5051 равна 11, она не делится на 3. Поэтому и число 5051 па 3 не делится. Проверьте!
Аналогично формулируется и признак делимости на 9.
На 9 делятся все те и только те числа, сумма цифр которых делится на 9.
Примеры: Число 5742 делится на 9, поскольку сумма его цифр 5 + 7 + 4 + 2 = 18, а 18 делится на 9. А число 5051 на 9 не делится, так как его сумма цифр 5 + 0 + 5+1 = 11, а 11 на 9 не делится.
Каждое число, которое делится на 9, называется кратным числа 9. Каждое число, которое делится на 3, называется кратным числа 3.
Вообще, если одно число делится на другое, то первое называется кратным другого.
3, 6, 9, 12, 15, 18, … – последовательность натуральных чисел, кратных 3. Таких чисел бесконечно много. Наименьшее из них число 3, наибольшего не существует.
Говорят: «кратное трех», но «кратно трем».
Если число 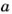
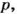
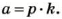
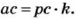
Если каждое из чисел 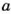
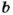
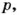
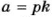
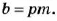
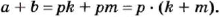
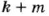
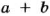
О признаках делимости на 4,6, 7,11,13 читайте на с. 37.
- Заказать решение задач по высшей математике
Выполнение заданий:
Пример №6
Какое утверждение верно:
а) если число делится на 9, то оно делится и на 3.
б) если число делится на 3, то оно делится и на 9?
Решение:
Если число делится на 9, то сумма его цифр делится на 9. Эта сумма делится и на 3. Поэтому первое утверждение верно.
Второе утверждение неверно. Например, 30 делится на 3, но не делится на 9.
Пример №7
Запишите наибольшее четырехзначное число, которое кратно 3, но не кратно 9.
Решение:
Наибольшее четырехзначное число 9999. Оно делится и на 9, и на 3. Если это число уменьшить на 3, то получим число 9996. Оно кратно 3, но не кратно 9.
Разложение чисел на простые множители
Какие простые числа нужно умножить, чтобы получить 15? Нетрудно догадаться, что такими числами являются 3 и 5. Следовательно, 15 = 3 • 5. Такое представление числа 15 называется его разложением на простые множители.
Другие примеры:
30 = 2 • 3 • 5; 45 = 3 • 3 • 5; 88 = 2 • 2 • 2 • 11.
Каждое составное число можно разложить на два или больше простых множителей.
Как это делать покажем на примере. Пусть нужно разложить па простые множители число 104. Пишем это число, и справа от него проводим вертикальную черту. По признаку делимости определяем, что число 104 делится на 2 – наименьшее простое число. За чертой пишем число 2, а 52 – частное отделения 104 на 2 – записываем под числом 104. То же самое делаем с частным 52 и новым частным 26. Разделив 26 на его наименьший делитель 2, получим простое число 13. Его пишем тоже справа от черты. 13 делится на 13. Частное равно 1. На этом процесс определения простых множителей числа 104 завершен. Все они записаны справа от черты. Итак, 104 = 2 • 2 • 2 • 13. Это и есть разложение числа 104 на простые множители.
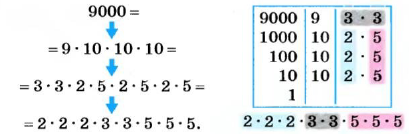
В отдельных случаях разложение числа на простые множители можно упростить. Например, число 9000 на простые множители можно разложить так:
Число 9000 раскладывается на восемь простых множителей. Каждый из них является делителем числа 9000. Вообще, каждый из множителей, на какие раскладывается число а, является делителем этого числа.
Разных простых делителей число 9000 имеет три: 2, 3 и 5. А разных натуральных делителей это число имеет очень много: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 4500, 9000.
Как вы уже знаете, произведение 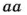
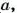
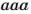
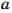
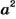
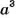
Аналогично,
Такие произведения равных чисел называют соответственно четвертой, пятой, шестой степенью числа
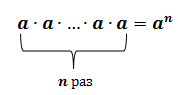
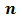
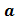
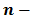
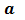
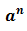
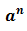
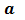
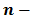
Используя понятие степени, разложение числа на простые множители можно записать короче:
Разложить на простые множители числа, которые делятся на 2, 3, 5, 9, 10, сравнительно несложно. В иных случаях это бывает сделать сложно. Попытайтесь, например, разложить на простые множители число 323. Специалисты, которым часто приходиться заниматься разложением чисел на множители, пользуются специальными таблицами. Часть такой таблицы (для небольших чисел, которые не делятся на 2, 3, 5) представлена на форзаце учебника. Пользуясь этой таблицей, можно сразу записать: 323 = 17 • 19.
Выполнение заданий:
Пример №8
Можно ли разложить на простые множители число 1?
Решение:
Нет, нельзя. Каждое простое число больше 1. А произведение чисел, каждое из которых больше 1, не может равняться 1.
Пример №9
Можно ли равенство 17=1 • 17 считать разложением числа на простые множители?
Решение:
Нельзя. Хотя в произведении 1 • 17 каждое число множитель, но первое из них – число не простое.
Пример №10
Разложите на простые множители число 600.
Решение:
Пример №11
Разложите на простые множители число 266.
Решение:
Число 266 делится на 2, поэтому 266 = 2 • 133. Число 133 не делится ни на какое из чисел 2, 3, 5. Его нет и в таблице простых чисел. Ищем его в таблице разложения чисел на простые множители: 133 = 7 • 19. Следовательно, 266 = 2 • 7 • 19.
Пример №12
Какое наименьшее трехзначное число можно разложить на два одинаковых простых множителя?
Решение:
7 • 7 = 49 – число не трехзначное, 11 • 11 = 121 – трехзначное. Значит искомое число равно 121.
Наибольший общий делитель
Часто возникает необходимость находить общие делители двух или нескольких чисел. Попытаемся найти, например, общие делители чисел 30 и 45.
30 делится на: 1 , 2, 3 , 5 , 6, 10, 15 , 30;
45 делится на: 1 , 3 , 5 , 9, 15 , 45.
Числа 30 и 45 имеют четыре общих делителя: 1, 3, 5 и 15. Наибольшее из этих четырех чисел 15. Это – наибольший общий делитель чисел 30 и 45.
Наибольшим общим делителем (ПОД) нескольких чисел называется наибольшее число, на которое делится каждое из данных чисел.
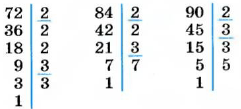
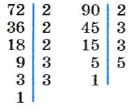
Найдем, например, НОД (72, 84, 90). Разложим каждое из этих чисел на простые множители:
Числа 72, 84, 90 имеют два общих простых делителя: 2 и 3. Умножив их, получим:
НОД (72, 84, 90) = 2 • 3 = 6.
Чтобы найти наибольший общий делитель нескольких чисел, необходимо разложить их на простые множители и умножить все их общие множители.
Найдем НОД (65, 32). Поскольку
65 = 5 • 13, 32 = 2 • 2 • 2 • 2 • 2,
то числа 65 и 32 имеют только один общий делитель – число 1. Поэтому НОД (65, 32) = 1.
Два числа, наибольший общий делитель которых равен 1, называются взаимно простыми. Числа 65 и 32 взаимно простыми.
Замечание. Не путайте взаимно простые числа с простыми. Некоторое число может быть простым, но не взаимно простым. (Взаимно – значит с каким-то другим.) Взаимно простыми могут быть и составные числа.
Взаимно простыми могут быть не только два числа, но и три, и больше. Например, числа 8, 9 и 25 – взаимно простые. Эти три числа не только взаимно простые, но и попарно взаимно простые, поскольку каждые два из них -числа взаимно простые. А вот числа 6, 8 и 9 – взаимно простые, но не попарно взаимно простые, поскольку НОД (6, 8) = 2, НОД (6, 9) = 3.
Выполнение заданий:
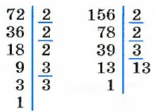
Пример №13
Найдите НОД (72, 156).
Решение:
В разложениях чисел 72 и 156 на простые множители общими являются такие простые множители: 2, 2 и 3.
Поэтому
Пример №14
Какое наибольшее количество одинаковых букетов можно составить из 6 васильков и 9 ромашек?
Решение:
Необходимо найти наибольшее число, на которое делится 6 и 9, то есть наибольший общий делитель этих чисел. НОД (6, 9) = 3. Следовательно, можно составить 3 букета (рис. 6)
Наименьшее общее кратное
Запишем несколько натуральных чисел, которые делятся на 8: 8, 16, 24, 32, 40, 48, 56, 64, … .
Каждое из этих чисел кратно 8. Любое число, которое делится на 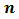
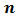
Числа, кратные 6,-это: 6, 12 , 18, 24 , 30, 36 , 42, 48…..
Числа, кратные 4, – это: 4,8, 12, 16, 20, 24 , 28, 32, 36 , … .
Общими кратными чисел 4 и 6 являются: 12, 24, 36 и много других чисел. Наибольшего общего кратного числа 6 и 4 не имеют. А наименьшее существует.
Наименьшим общим кратным (НОК) нескольких чисел называется такое наименьшее натуральное число, которое делится на каждое данное число. НОК (4, 6) = 12.
Наименьшее общее кратное двух чисел можно найти, разложив эти числа на простые множители. Найдем, например, НОК (72, 90). Для этого разложим числа 72 и 90 на простые множители. Их НОК должно содержать все простые множители числа 72 и все простые множители числа 90. Следовательно, 35 чтобы найти НОК (72, 90), необходимо простые множители числа 72 дополнить такими простыми множителями числа 90, которых нет в разложении числа 72. В данном случае к произведению 2 • 2 • 2 • 3 • 3 надо дописать множитель 5. Имеем: НОК (72, 90) = 2 • 2 • 2 • 3 • 3 • 5 = 72 • 5 = 360.
Наименьшее общее кратное двух взаимно простых чисел равно их произведению. Например, НОК (5, 8) = 40. Почему?
А как найти НOK трех чисел?
Чтобы найти наименьшее общее кратное чисел 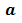
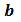
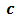
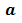
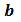
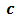
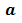
Найдем, например, НОК чисел 72, 90 и 80. Поскольку
72 = 2 • 2 • 2 • 3 • 3,
90 = 2 • 3 • 3 • 5,
80 = 2 • 2 • 2 • 2 • 5,
то НОК (72, 90, 80) = 2 • 2 • 2 • 3 • 3 • 5 • 2 = 720.
Рассмотрим пример. Пусть 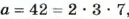
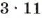
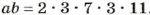
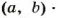
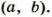
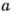
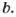
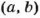
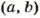
Поэтому, чтобы найти наименьшее общее кратное двух чисел, можно произведение этих чисел разделить на их наибольший общий делитель.
Из этого утверждения вытекают важные следствия:
- Если НОД
= 1, то НОК
- Если число
делится на
, то НОК
Выполнение заданий:
Пример №15
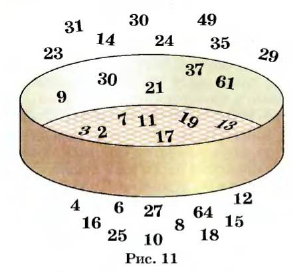
Найдите наибольшее двузначное число, кратное чисел 2 и 7.
Решение:
Если число 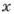
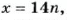
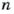
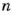
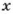
Ответ. 98.
Пример №16
Во время тренировки на стадионе два велосипедиста стартовали одновременно. Первый велосипедист проезжает полный круг за 75 с, а второй — за 100 с. Через какое время велосипедисты вновь встретятся на старте?
Решение:
Искомый интервал времени должен быть кратным чисел 75 и 100. Найдем НОК (75, 100).
75 = 3 • 5 • 5, 100 = 2 • 2 • 5 • 5. IIOK (75, 100) = 100 • 3 = 300. 300 с = 5 мин.
Следовательно, спустя 5 мин велосипедисты вновь встретятся на старте.
Исторические сведения:
Деление натуральных чисел некоторые ученые древности умели выполнять еще несколько тысячелетий назад. Это математическое действие тогда считалось наиболее трудным, поскольку люди не знали современных правил деления, а числа записывали не так, как их записывают теперь. Попытайтесь, например, разделить число 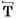
Признаки делимости на 2 и на 9 древнегреческие математики знали еще в III в. до н. э. Только формулировали их не так, как теперь. Издавна известны и другие признаки делимости.
На 4 делятся все те и только те числа, в которых две последние цифры выражают число, которое делится на 4.
На в делятся все те и только те числа, которые делятся и на 2, и на 3.
Интересный признак делимости на 7, 11 и 13. Пусть имеется какое-то число, например 1 057 958. Отделив три последние цифры, разобьем данное число на два меньших: 1057 и 958. Если разность образованных таким способом чисел делится на 7, 11 или 13, то и данное число делится соответственно на 7, 11 или 13. Поскольку разность 1057 – 958 равна 99, а 99 делится на 11 и не делится на 7 и 13, то и данное число делится на 11, но не делится на 7 и 13. Проверьте!
Простые числа были известны еще в VI в. до н. э. Евклид в III в. до н. э. доказал, что множество простых чисел бесконечно, то есть последовательность
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, … не имеет конца.
Интересный способ составления таблиц простых чисел предложил в III в. до н. э. Оратосфен. Выписав подряд все натуральные числа от 2 до какого-то 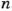
Отсеивание составных чисел образно показано па рисунке 11.
Поэтому такой способ составления таблиц простых чисел назвали «решетом Эратосфена». Ниже показано, как с помощью «решета Эратосфена» можно составить таблицу простых чисел, меньших 40.
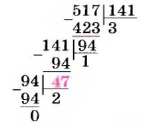
Раскладывать числа на простые множители древнегреческие математики умели еще в VI в. до н. э. Интересный способ нахождения НОД предложил Евклид. Пусть, надо найти НОД (517, 141). Для этот делим большее число на меньшее, меньшее – на полученный первый остаток, первый остаток – на второй и т. д. Последний отличный от 0 остаток – искомый НОД.
В данном примере НОД (517, 141) = 47. Математики и теперь часто используют этот способ, его называют алгоритмом Евклида.
Главное в разделе:
Если числа 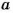
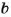
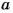
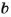
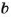
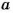
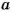
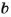
Каждое число, которое делится только на 1 и на само себя, называют простым. Если число имеет более двух делителей, его называют составным. Число 1 имеет только один делитель, оно – ни простое, ни составное.
2, 3, 5, 7, 11, 13, 17, 19, … – последовательность простых чисел. Простых чисел бесконечно много.
На 2 делятся все те и только те числа, которые оканчиваются четной цифрой. Четные цифры: 0, 2, 4, 6, 8. Все остальные цифры (1, 3, 5, 7, 9) – нечетные. Числа, которые делятся на 2, называются четными, а которые не делятся на 2, нечетными.
1, 3, 5, 7, 9, 11, 13,… – последовательность нечетных чисел;
0, 2, 4, 6, 8, 10, 12,… – последовательность четных чисел.
На 5 делятся все те и только те числа, которые оканчиваются цифрой 5 или 0.
На 10 делятся все те и только те числа, которые оканчиваются цифрой 0.
На 3 делятся все те и только те числа, сумма цифр которых делится на 3.
На 9 делятся все те и только те числа, сумма цифр которых делится на 9.
Если каждое слагаемое делится на некоторое число, то их сумма тоже делится на это число. Если хотя бы один из множителей делится на некоторое число, то и все произведение делится на это число.
Разложить число на простые множители – это значит представить его в виде произведения простых чисел. Например, 2 • 3 • 5 -разложение на простые множители числа 30.
Наибольшее число, на которое делится каждое из данных чисел, называется наибольшим общим делителем этих чисел (НОД). Чтобы найти НОД нескольких чисел, надо разложить их на простые множители и умножить все их общие множители. Два числа, НОД которых равен 1, называют взаимно простыми. Например, числа 15 и 32 – взаимно простые, потому что НОД (15, 32) =1.
Наименьшим общим кратным нескольких чисел (НОК) называют наименьшее натуральное число, которое делится на каждое из данных чисел. Чтобы найти НОК чисел 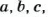
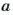
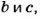
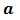
- Выражения и уравнения
- Линейное уравнение с одной переменной
- Целые выражения
- Одночлены
- Делимость чисел в математике
- Обыкновенные дроби
- Отношения и пропорции
- Рациональные числа и действия над ними

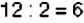
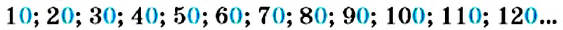
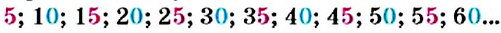
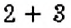


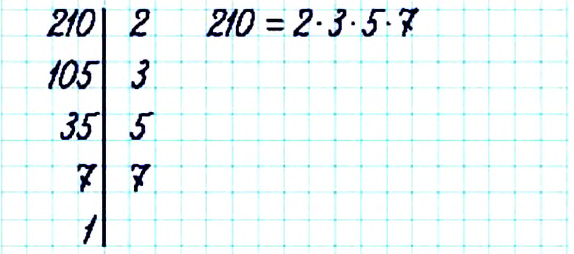
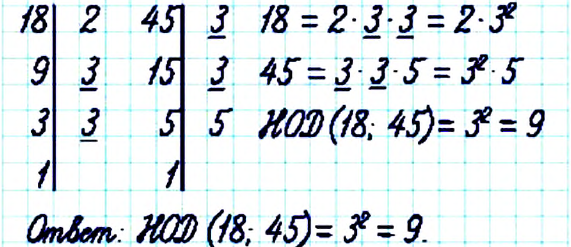
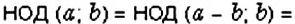
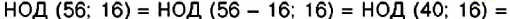
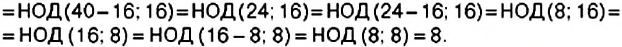
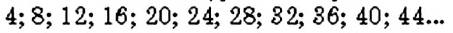
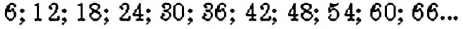
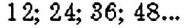
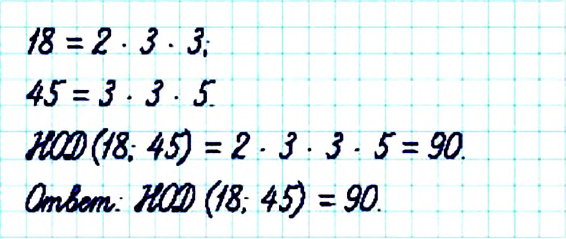
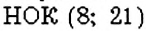
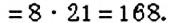
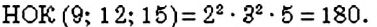
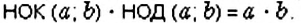
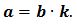
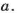


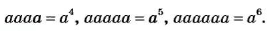
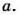
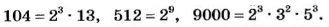
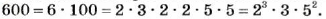
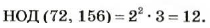

 = 1, то НОК
= 1, то НОК 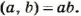
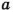 делится на
делится на 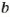 , то НОК
, то НОК