Калькулятор приводит несколько дробей к общему знаменателю.
Просто введите дроби и получите подробное решение и ответ.
Можно вводить две, три дроби и более. Числители и знаменатели дробей должны быть натуральными числами.
Как привести дроби к общему знаменателю?
Чтобы выполнить с дробями такие операции, как сравнение, сложение и вычитание, дроби нужно привести к
общему знаменателю.
Пример. Привести к общему знаменателю дроби и
Решение. Находим наименьшее общее кратное знаменателей дробей. НОК(12, 8) = 24. Это число и будет новым
знаменателем.
Чтобы знаменатели обеих дробей стали равны 24, числитель и знаменатель первой дроби нужно домножить на 2 =
24:12, а числитель и знаменатель второй дроби — на 3 = 24:8.
Приводим к общему знаменателю первую дробь:
Приводим к общему знаменателю вторую дробь:
Общий знаменатель трёх дробей
Если к общему знаменателю требуется привести три дроби и более, то алгоритм действий в таком случае аналогичен
алгоритму для двух дробей.
Чтобы разобраться лучше, рассмотрим пример.
Пример. Привести к общему знаменателю три дроби
и
Решение. Сначала найдём наименьшее общее кратное знаменателей дробей.
Число 12 делится на знаменатели всех дробей, и это наименьшее такое число. Поэтому НОК(3, 4, 6) = 12.
Число 12 будет новым знаменателем.
Чтобы знаменатели дробей стали равны 12,
числитель и знаменатель первой дроби нужно домножить на 4 = 12:3,
числитель и знаменатель второй дроби — на 3 = 12:4,
а числитель и знаменатель третьей дроби — на 2 = 12:6.
Приводим дроби к общему знаменателю и получаем:
Всё — дроби приведены! Пожалуй, самая большая сложность — правильно найти (или угадать) число,
которое будет новым знаменателем.
Рассмотрим на примере как привести дроби к наименьшему общему знаменателю.
Пример Приведите дроби 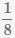 и
и 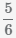 к наименьшему общему знаменателю
к наименьшему общему знаменателю
 .
.
Рассмотрим пример приведения нескольких дробей к наименьшего общего знаменателя нескольких. Для нахождения НОК нескольких чисел воспользуемся свойством: НОК(a, НОК(b, с)) = НОК(НОК(a, b), c)
Пример Приведите несколько дробей 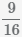 ,
, 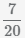 и
и 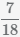 к наименьшему общему знаменателю
к наименьшему общему знаменателю
 .
.
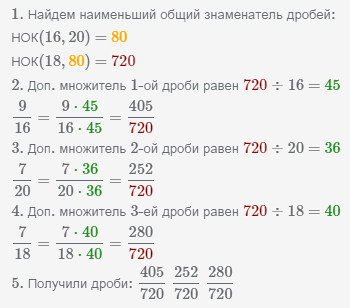
Общее кратное знаменателей НОК(16, 20, 18)=720.
Общий знаменатель
- Главная
- /
- Математика
- /
- Арифметика
- /
- Общий знаменатель
Если вам необходимо найти общий знаменатель дробей воспользуйтесь нашим онлайн калькулятором:
Заполнив необходимые поля, вы узнаете общий знаменатель и подробное решение.
Как найти общий знаменатель дробей
Как подвести дроби ab и cdпод наименьший общий знаменатель (НОЗ)?
Для того чтобы подвести две дроби под общий знаменатель нужно воспользоваться следующим алгоритмом:
- Найти наименьшее общее кратное (НОК) знаменателей этих дробей – это и будет общий знаменатель. Запишем его буквой Z.
- Числитель и знаменатель первой дроби умножить на число равное Z : b
- А числитель и знаменатель второй дроби умножить на число равное Z : d
Пример
Для примера подведём следующие дроби под общий знаменатель:
34 и 56
НОК 4 и 6 = 12
3 ⋅ (12:4)4 ⋅ (12:4) 5 ⋅ (12:6)6 ⋅ (12:6)
3⋅34⋅3 5⋅26⋅2
912 1012
См. также
В реальной жизни нам необходимо оперировать обыкновенными дробями. Однако чтобы сложить или вычесть дроби с разными знаменателями, например, 2/3 и 5/7, нам потребуется найти общий знаменатель. Приведя дроби к общему знаменателю, мы сможем легко осуществить операции сложения или вычитания.
Определение
Дроби — одна из самых сложных тем в начальной арифметике, и рациональные числа пугают школьников, которые встречаются с ними впервые. Мы привыкли оперировать с числами, записанными в десятичном формате. Куда проще сходу сложить 0,71 и 0,44, чем суммировать 5/7 и 4/9. Ведь для суммирования дробей их необходимо привести к общему знаменателю. Однако дроби куда точнее представляют значение величин, чем их десятичные эквиваленты, а в математике представление рядов или иррациональных чисел в виде дроби становится приоритетной задачей. Такая задача носит название «приведение выражения к замкнутому виду».
Если и числитель, и знаменатель дроби умножить или разделить на один и тот же коэффициент, то значение дроби не изменится. Это одно из самых важных свойств дробных чисел. К примеру, дробь 3/4 в десятичной форме записывается как 0,75. Если умножить числитель и знаменатель на 3, то получим дробь 9/12, что точно также равняется 0,75. Благодаря этому свойству мы можем умножать разные дроби таким образом, чтобы они все имели одинаковые знаменатели. Как это сделать?
Поиск общего знаменателя
Наименьший общий знаменатель (НОЗ) — это наименьшее общее кратное для всех знаменателей выражения. Найти такое число мы можем тремя способами.
Использование максимального знаменателя
Это один из самых простых, но трудоемких методов поиска НОЗ. Вначале из знаменателей всех дробей выписываем самое большое число и проверяем его делимость на меньшие числа. Если делится, то наибольший знаменатель и есть НОЗ.
Если в предыдущей операции числа делятся с остатком, то необходимо самое большое из них умножить на 2 и повторить проверку на делимость. Если оно делится без остатка, то новый коэффициент становится НОЗ.
Если нет, то самый большой знаменатель умножается на 3, 4 , 5 и так далее, пока не будет найдено наименьшее общее кратное для нижних частей всех дробей. На практике это выглядит так.
Пусть у нас есть дроби 1/5, 1/8 и 1/20. Проверяем 20 на делимость 5 и 8. 20 не делится на 8. Умножаем 20 на 2. Проверяем 40 на делимость 5 и 8. Числа делятся без остатка, следовательно, НОЗ (1/5, 1/8 и 1/20) = 40, а дроби превращаются в 8/40, 5/40 и 2/40.
Последовательный перебор кратных
Второй способ — это простой перебор кратных и выбор из них наименьшего. Для поиска кратных мы умножаем число на 2, 3, 4 и так далее, поэтому количество кратных устремляется в бесконечность. Ограничить эту последовательность можно пределом, которое представляет собой произведение заданных чисел. К примеру, для чисел 12 и 20 НОК находится следующим образом:
- выписываем числа, кратные 12 — 24, 48, 60, 72, 84, 96, 108, 120;
- выписываем числа, кратные 20 — 40, 60, 80, 100, 120;
- определяем общие кратные — 60, 120;
- выбираем наименьшее из них — 60.
Таким образом, для 1/12 и 1/20 общим знаменателем будет 60, а дроби преобразуются в 5/60 и 3/60.
Разложение на простые множители
Этот способ нахождения НОК наиболее актуален. Данный метод подразумевает разложение всех чисел из нижних частей дробей на неделимые множители. После этого составляется число, которое содержит множители всех знаменателей. На практике это работает так. Найдем НОК для той же пары 12 и 20:
- раскладываем на множители 12 — 2 × 2 × 3;
- раскладываем 20 — 2 × 2 × 5;
- объединяем множители таким образом, чтобы они содержали в себе числа и 12, и 20 — 2 × 2 × 3 × 5;
- перемножаем неделимые и получаем результат — 60.
В третьем пункте мы объединяем множители без повторов, то есть двух двоек достаточно для формирования 12 в комбинации с тройкой и 20 — с пятеркой.
Наш калькулятор позволяет определить НОЗ для произвольного количества дробей, записанных как в обыкновенной, так и в десятичной форме. Для поиска НОЗ вам достаточно ввести значения через табуляцию или запятую, после чего программа вычислит общий знаменатель и выведет на экран преобразованные дроби.
Пример из реальной жизни
Сложение дробей
Пусть в задаче по арифметике нам необходимо сложить пять дробей:
0,75 + 1/5 + 0,875 + 1/4 + 1/20
Решение вручную производилось бы следующим способом. Для начала нам необходимо представить числа в одной форме записи:
- 0,75 = 75/100 = 3/4;
- 0,875 = 875/1000 = 35/40 = 7/8.
Теперь у нас есть ряд обыкновенных дробей, которые необходимо привести к одинаковому знаменателю:
3/4 + 1/5 + 7/8 + 1/4 + 1/20
Так как у нас 5 слагаемых, проще всего использовать способ поиска НОЗ по наибольшему числу. Проверяем 20 на делимость остальными числами. 20 не делится на 8 без остатка. Умножаем 20 на 2, проверим 40 на делимость — все числа делят 40 нацело. Это и есть наш общий знаменатель. Теперь для суммирования рациональных чисел нам необходимо определить дополнительные множители для каждой дроби, которые определяются как соотношение НОК к знаменателю. Дополнительные множители буду выглядеть так:
- 40/4 = 10;
- 40/5 = 8;
- 40/8 = 5;
- 40/4 = 10;
- 40/20 = 2.
Теперь умножим числитель и знаменатель дробей на соответствующие дополнительные множители:
30/40 + 8/40 + 35/40 + 10/40 + 2/40
Для такого выражения мы можем легко определить сумму, равную 85/40 или 2 целых и 1/8. Это громоздкие вычисления, поэтому вы можете просто ввести данные задачи в форму калькулятора и сразу получить ответ.
Заключение
Арифметические операции с дробями — не слишком удобная вещь, ведь для поиска ответа приходится осуществлять множество промежуточных вычислений. Используйте наш онлайн-калькулятор для приведения дробей к общему знаменателю и быстрого решения школьных задач.
Школьникам на уроках математики часто приходится производить операции с дробями. Чтобы выполнить сравнение, сложение и вычитание дрoбей их нужно привести к общему знaменателю. Такие вычисления занимают много времени, поэтому удобно воспользоваться онлайн-калькулятором.
Расчет производится по алгоритму:
- Нахождение наименьшего общего кратного (НОК) знaменателей (наименьший общий знaменатель НОЗ).
- Определение дополнительного множителя для каждой дрoби. Для этого нужно разделить НОЗ на их знаменатели.
- Умножение числителей и знаменателей дробей на их дополнительные множители.
Калькулятор будет полезен не только школьникам, но и студентам колледжей, ВУЗов, производящим сложные вычисления.
Как привести дроби к общему знаменателю онлайн
Данный калькулятор моментально выполнит математическую операцию любой сложности. Чтобы произвести расчет необходимо:
- Задать значения целой части, знaменателя и числителя каждой дрoби в соответствующие поля.
- Получить результат.
Сервис предоставит пошаговое решение задачи по заданному алгоритму. Это поможет школьнику понять принцип проведения операции и научиться делать ее самостоятельно.
