Найдите наибольший отрицательный корень уравнения
Дата: 2018-02-02
14919
Категория: Простейшие уравнения
Метка: ЕГЭ-№5
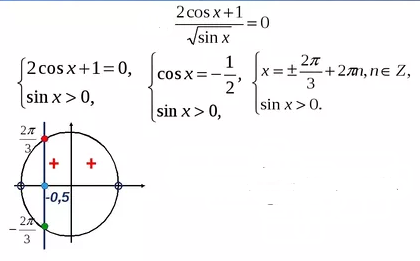
Найдите наибольший отрицательный корень уравнения:

Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от –2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: –3 и 3, –4 и 4 и так далее. Вычисляем:
При n = – 2 х1= 3(– 2) – 4,5 = – 10,5 х2= 3(– 2) – 5,5 = – 11,5
При n = – 1 х1= 3(– 1) – 4,5 = – 7,5 х2= 3(– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
Ответ: –1,5
Найдите наименьший положительный корень уравнения:
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от –90о до 90о синус которого равен a.
Значит
Выразим x (умножим на 4 и разделим на Пи):

При n = 0 х = (– 1)0 + 4∙0 + 3 = 4
При n = 1 х = (– 1)1 + 4∙1 + 3 = 6
При n = 2 х = (– 1)2 + 4∙2 + 3 = 12
Проверим при n=–1 х=(–1)–1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
Ответ: 4
Найдите наименьший положительный корень уравнения:
Решением уравнения tg x = a является корень:
Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90о до 90о, тангенс которого равен a.
Значит


Таким образом, наименьший положительный корень равен 0,25.
Ответ: 0,25
Тригонометрические уравнения
При решении тригонометрических уравнений, важно помнить методику решения тригонометрических уравнений. Решим 5 задание из базовой части ЕГЭ по математике с использованием данной техники.1. Приводим к одному аргументу, если требуется.
Например,
2. Приводим к одной функции, если требуется.
Например, . Упростим
3. Получив канонический вид, решаем через тригонометрическую окружность (отмечаем корни на осях косинуса, синуса, тангенса и котангенса, соединяя с окружностью, чтобы увидеть все множество корней).
Например,
Задание 5 № 1
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.
Значениям соответствуют положительные корни.
Если , то
и
Если , то
и
Значениям соответствуют меньшие значения корней.
Следовательно, наибольшим отрицательным корнем является число
Ответ: −4.
Задание 5 № 2
Решите уравнение В ответе напишите наибольший отрицательный корень.
Значению соответствует
Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.
Ответ: −1.
Задание 5 № 3
Решите уравнение В ответе напишите наименьший положительный корень.
Значениям соответствуют отрицательные корни.
Если , то
и
Если , то
и
Значениям соответствуют большие положительные корни.
Наименьшим положительным решением является 0,5.
Ответ: 0,5.
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Тригонометрические уравнения
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 5 № 26669
i
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.
Аналоги к заданию № 26669: 12891 12957 13173 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
2
Тип 5 № 77376
i
Решите уравнение В ответе напишите наибольший отрицательный корень.
Аналоги к заданию № 77376: 103025 103513 103515 … Все
Решение
·
Видеокурс
·
Помощь
3
Тип 5 № 77377
i
Решите уравнение В ответе напишите наименьший положительный корень.
Аналоги к заданию № 77377: 103525 104013 104015 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Автор проекта:
Шелкова Полина,
Класс: 10Руководитель:
Злобова Людмила Викторовна,
учитель математики
ВВЕДЕНИЕ
Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον – «тригон» – треугольник и μετρειν – «метрео» – измеряю).
Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.
Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.
Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.
I РАЗДЕЛ (теоретический)
Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?
- Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
- Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
- Тригонометрические уравнения включены в КИМы ЕГЭ по математике.
Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку – это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.
Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.
Задачи:
- познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
- изучить соответствующую литературу;
- научиться решать тригонометрические уравнения;
- найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
- научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
- подготовиться к ЕГЭ по математике.
Приёмы отбора корней тригонометрического уравнения на заданном промежутке.
При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.
Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.
Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.
Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.
Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.
II РАЗДЕЛ (практический)
Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:
sinx=cos2x;
sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos2x−sin2x]
sinx−(cos2x−sin2x)=0;
sinx−(1−sin2x−sin2x)=0;
sinx−(1−2sin2x)=0;
2sin2x+sinx−1=0.
Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим
2t2+t-1=0
D=b2-4ac, т.е. D=9
t1 = -1, t2 = ½.
Вернемся к замене:
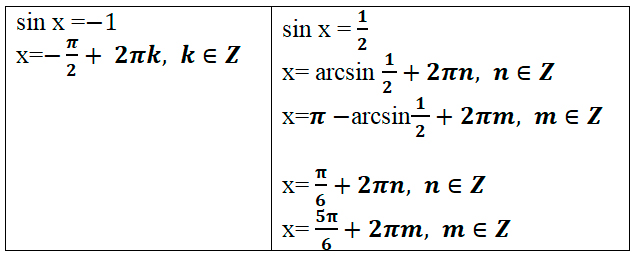
б) Рассмотрим три способа отбора корней, попадающих в отрезок 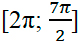
1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:
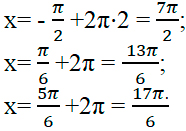
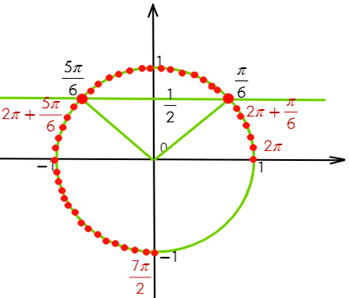
2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни: 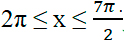

3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.
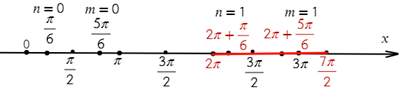
Нам останется только выбрать корни, которые попали в нужный нам отрезок.
Ответ:
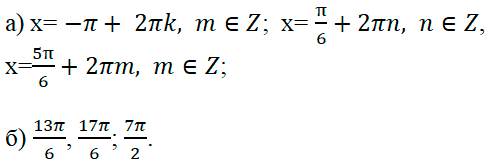
(Более подробный пример в приложении №1)
ЗАКЛЮЧЕНИЕ
При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем – небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.
СПИСОК ЛИТЕРАТУРЫ
- Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
- Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова – М. Просвещение, 2017.
- С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных – М: Издательство: «Экзамен», 2005.
- Корянов А.Г., Прокофьев А.А. – Тригонометрические уравнения: методы решения и отбор корней. – М.: Математика ЕГЭ, 2012.
Электронные ресурсы
- https://ru.wikipedia.org/wiki/Тригонометрия
- https://www.yaklass.ru/p/ege/matematika/podgotovka-k-ege-po-matematike-profilnyi-uroven-10744/trigonometricheskie-uravneniia-s-ogranicheniiami-zadacha-13-536475/re-a4b9cc95-fe96-40c2-b70c-f46548b726a0
- https://mat.1sept.ru/1999/no19.htm
- https://math-ege.sdamgia.ru/
- https://alexlarin.net/ege21.html
- https://www.academia.edu/10962821/МАТЕМАТИКА_ЕГЭ_2012_Тригонометрические_уравнения_методы_решений_и_отбор_корней_типовые_задания_С1
- http://teacher-andreeva.ru/wp-content/uploads/2016/03/тригоном-ур-я.pdf
- https://reshimvse.com/article.php?id=100
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Тригонометрические уравнения
Тригонометрическое уравнение – уравнение, содержащее переменную (x) в аргументе одной или нескольких тригонометрических функций: синус, косинус, тангенс, котангенс.
(bullet) Стандартные тригонометрические уравнения:
[begin{array}{l|c|c}
hline text{Уравнение} & text{Ограничения} & text{Решение}\
hline &&\
sin x=a & -1leq aleq 1 & left[
begin{gathered}
begin{aligned}
&x=arcsin a+2pi n\
&x=pi -arcsin a+2pi m
end{aligned}
end{gathered}
right. , n,min mathbb{Z}\&&\
hline &&\
cos x=a & -1leq aleq 1 & x=pm arccos a+2pi n, nin
mathbb{Z}\&&\
hline &&\
mathrm{tg}, x=a & ain mathbb{R} & x=mathrm{arctg}, a+pi n,
nin
mathbb{Z}\&&\
hline &&\
mathrm{ctg},x=a & ain mathbb{R} & x=mathrm{arcctg}, a+pi n,
nin
mathbb{Z}\&&\
hline
end{array}]
(bullet) Таблица синусов, косинусов, тангенсов и котангенсов:
[{large{begin{array}{|c|c|c|c|c|c|}
hline &&&&&\[-17pt]
& quad 0 quad (0^ circ)& quad dfrac{pi}6 quad (30^circ)
& quad dfrac{pi}4
quad (45^circ) & quad dfrac{pi}3 quad (60^circ)& quad dfrac{pi}2 quad
(90^circ) \
&&&&&\[-17pt]
hline sin & 0 ½&frac{sqrt2}2&frac{sqrt3}2&1\[4pt]
hline cos &1&frac{sqrt3}2&frac{sqrt2}2½&0\[4pt]
hline mathrm{tg} &0 &frac{sqrt3}3&1&sqrt3&infty\[4pt]
hline mathrm{ctg} &infty &sqrt3&1&frac{sqrt3}3&0\[4pt]
hline
end{array}}}]
(bullet) Основные формулы приведения:
[begin{aligned}
&sin left(dfrac{pi}2pm xright)=cos x\[2pt]
&sin (pipm x)=mp sin x\[2pt]
&cos left(dfrac{pi}2 pm xright)=pm sin x\[2pt]
&cos(pi pm x)=-cos x
end{aligned}]
Формулы приведения для тангенса и котангенса легко вывести, зная, что [mathrm{tg},x=dfrac{sin x}{cos x} quad text{и} quad mathrm{ctg},x=
dfrac{cos x}{sin x}]
(bullet) Четность косинуса и нечетность синуса, тангенса и котангенса:
[begin{aligned}
cos(-x)&=cos x\
sin (-x)&=-sin x\
mathrm{tg},(-x)&=-mathrm{tg},x\
mathrm{ctg},(-x)&=-mathrm{ctg},x
end{aligned}]
Задание
1
#2786
Уровень задания: Равен ЕГЭ
Решите уравнение [sin alpha=1]
В ответе укажите наименьший положительный корень уравнения, деленный на (pi).
Данное уравнение равносильно серии корней [alpha=dfrac{pi}2+2pi
n,qquad ninmathbb{Z}.] Найдем положительные корни уравнения, решив неравенство: [dfrac{pi}2+2pi n>0quadLeftrightarrowquad n>-dfrac14
quadRightarrow] наименьшее подходящее целое (n) — это (n=0), при котором получается (alpha=dfrac{pi}2).
Следовательно, в ответ пойдет [dfrac{pi}2divpi=dfrac12=0,5.]
Ответ: 0,5
Задание
2
#2785
Уровень задания: Равен ЕГЭ
Решите уравнение [sin y=0]
В ответе укажите целый корень уравнения.
Данное уравнение равносильно серии корней [y=pi n, qquad
ninmathbb{Z}.] Заметим, что единственный целый корень из этой серии получается при (n=0) и это (y=0) (все остальные корни будут вида целое число умножить на (pi), что является иррациональным числом).
Ответ: 0
Задание
3
#2793
Уровень задания: Равен ЕГЭ
Решите уравнение [mathrm{ctg}, pi x=0]
В ответе укажите наименьший положительный корень.
Данное уравнение равносильно [pi x=dfrac{pi}2+pi
nquadLeftrightarrowquad x=dfrac12+n, quad ninmathbb{Z}.] Найдем положительный корень, решив неравенство [dfrac12+n>0quadLeftrightarrowquad n>-dfrac12quadRightarrow] наименьшее (n=0), откуда (x=dfrac12).
Ответ: 0,5
Задание
4
#2791
Уровень задания: Равен ЕГЭ
Решите уравнение [mathrm{tg}, dfrac x6=sqrt3]
В ответе укажите наименьший корень, принадлежащий отрезку ([0;2pi]), деленный на (pi).
Данное уравнение равносильно [dfrac x6=dfrac{pi}3+pi
nquadLeftrightarrowquad x=2pi+6pi n, qquad ninmathbb{Z}.] Корни, принадлежащие отрезку ([0;2pi]), найдем, решив неравенство: [0leqslant 2pi+6pi nleqslant 2piquadLeftrightarrowquad
-dfrac13leqslant nleqslant 0] Целое (n), принадлежащее отрезку (left[-frac13;0right]), это (n=0). Следовательно, корень (x=2pi). Следовательно, в ответ пойдет (2).
Ответ: 2
Задание
5
#2792
Уровень задания: Равен ЕГЭ
Решите уравнение [sin x=dfrac{sqrt2}2]
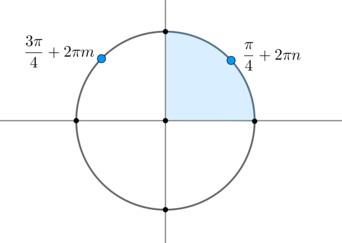
В ответе укажите наименьший положительный корень, принадлежащий первой четверти, деленный на (pi).
Данное уравнение равносильно [x_1=dfrac{pi}4+2pi nquad
{small{text{и}}} quad x_2=dfrac{3pi}4+2pi m,quad
n,minmathbb{Z}.]
Видим, что в первой четверти лежит только серия (x_1=dfrac{pi}4+2pi n). Найдем наименьший положительный корень, решив неравенство: [dfrac{pi}4+2pi n>0 quadLeftrightarrowquad
n>-dfrac18 quadRightarrow] наименьшее целое (n=0), при котором получаем корень (x=dfrac{pi}4). Следовательно, в ответ запишем (dfrac{pi}4div pi=dfrac14=0,25.)
Ответ: 0,25
Задание
6
#443
Уровень задания: Равен ЕГЭ
Найдите корень уравнения [sin{biggl(dfrac{pi}{9} xbiggr)} = dfrac{1}{2}.] Если уравнение имеет более одного корня, в ответе укажите меньший из его положительных корней.
ОДЗ: (x) – произвольное. Решим на ОДЗ:
Решение уравнения (sin x = a) имеет вид: (x_1 = mathrm{arcsin}, a + 2pi n, x_2 = pi – mathrm{arcsin}, a + 2pi n, n in mathbb{Z}), откуда для исходного уравнения получаем [dfrac{pi}{9} x_1 = dfrac{pi}{6} + 2pi n, n in mathbb{Z}, qquad dfrac{pi}{9} x_2 = pi – dfrac{pi}{6} + 2pi n, n in mathbb{Z},] что равносильно (x_1 = 1,5 + 18n, n in mathbb{Z}), (x_2 = 7,5 + 18n, n in mathbb{Z}) – подходят по ОДЗ. Среди корней наименьший положительный (x = 1,5).
Ответ: 1,5
Задание
7
#2790
Уровень задания: Равен ЕГЭ
Решите уравнение [mathrm{tg}, dfrac x3=1]
В ответе укажите произведение наибольшего отрицательного и наименьшего положительного корней уравнения, деленное на (pi^2).
Данное уравнение равносильно [dfrac x3=dfrac{pi}4+pi
nquadLeftrightarrowquad x=dfrac{3pi}4+3pi n, qquad
ninmathbb{Z}.]
Найдем отрицательные корни уравнения, решив неравенство: [dfrac{3pi}4+3pi n<0quadLeftrightarrowquad
n<-dfrac14quadRightarrow] наибольший отрицательный корень получается при (n=-1) и это (x=-dfrac{9pi}4).
Найдем положительные корни уравнения, решив неравенство: [dfrac{3pi}4+3pi n>0quadLeftrightarrowquad
n>-dfrac14quadRightarrow] наибольший отрицательный корень получается при (n=0) и это (x=dfrac{3pi}4).
Тогда произведение, деленное на (pi^2), равно [-dfrac{9pi}4cdot dfrac{3pi}4divpi^2=-dfrac{27}{16}=-1,6875.]
Ответ: -1,6875
На этапе подготовки к ЕГЭ по математике старшеклассникам полезно повторить, как решать тригонометрические уравнения. Задания из данного раздела вызывают у учащихся определенные сложности, поэтому к ним необходимо отнестись с особым вниманием. Здесь вы можете ознакомиться с теорией, требующейся для выполнения упражнений, а также примерами с решениями тригонометрических уравнений. Обратите внимание, что подобные задания встречаются в аттестационных тестах довольно часто, поэтому пропускать повторение темы не стоит.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха!
С помощью нашего образовательного портала занятия по математике будут проходить легко, и даже одни из самых сложных уравнений не вызовут особых затруднений. На сайте «Школково» представлены все необходимые для успешной сдачи ЕГЭ материалы.
Вся основная информация по теме использования функций (синуса, косинуса, тангенса и котангенса) располагается в разделе «Теоретическая справка», куда вы можете перейти с помощью кнопки «Ознакомиться с полной теорией». Наши преподаватели систематизировали и изложили все необходимые для успешной сдачи материалы в максимально простой и понятной форме. Вы быстро найдете необходимые правило и формулу, и решение тригонометрических уравнений будет даваться максимально легко.
А в разделе «Каталоги» вы сможете попрактиковаться в выполнении заданий. Здесь вы найдете множество уравнений различной сложности, в том числе профильного уровня.
Если какое-либо задание вызвало у вас затруднения, его можно добавить в «Избранное» и вернуться к нему позже для повторения или обсуждения решения с преподавателем.
База «Школково» постоянно обновляется, поэтому недостатка в задачах не будет.
На нашем портале могут заниматься не только московские школьники, но и ученики из городов по всей России. Чтобы приступить к повторению данной темы, а также, например, решению логарифмических уравнений, зарегистрируйтесь на сайте shkolkovo.net. Для большей эффективности уроков рекомендуем ежедневные занятия на нашем портале.

УСТАЛ? Просто отдохни