Как найти наименьший периметр квадрата

Формула периметра прямоугольника

Для начала вспомним формулу периметра.

В геометрии периметр любой фигуры равен сумме длин его сторон.

У прямоугольника 4 стороны: 2 длины и 2 ширины.

Обозначим длину как а, ширину – как b. Периметр обозначается заглавной буквой Р.

Отсюда получаем:

Р = а + а + b + b = 2*a + 2*b = 2*(a + b);

Итак, формула периметра прямоугольника:

Р = 2*(a + b);

Формула периметра квадрата

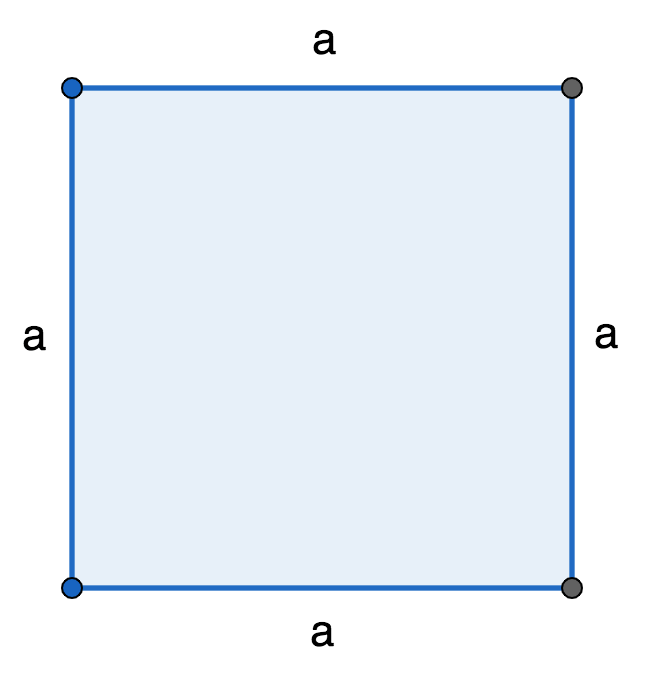
Формула периметра квадрата находится аналогичным способом. Так как все его стороны равны, 1 его сторону берем за а. Тогда периметр квадрата равен:

Р = а + а + а + а = 4*а;

Если у квадрата все 4 стороны равны, следовательно, длина его сторон должна быть кратна длине и ширине прямоугольников, которые образуют данный квадрат.

В данном случае, сторона квадрата должна быть кратна длине (18 см) и ширине (8 см) прямоугольников, на которые он делится. То есть сторона квадрата должна делиться одновременно и на длину прямоугольников, и на ширину прямоугольников без остатка.

Итак, найдем наименьшее общее кратное (НОК) чисел 18 и 8.

НОК (18; 8) = 72;

Итак, сторона квадрата должна составлять как минимум 72 см. Она может быть также равна:

• 72 * 2 = 144 см;
• 72 * 3 = 216 см;
• 72 * 4 = 288 см и т. д.

Наименьшим возможным значением при этом является 72. 

Найдем периметр данного квадрата со стороной 72 см. Он будет равен:

Р = 4*а = 4 * 72 = 288 см.

Ответ: 288 см.

Периметр

Периметр — это сумма длин всех сторон многоугольника.

Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.

Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».

Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.

AB = 3 см, BC = 7 см

P_ABCD = (AB + BC) · 2
P_ABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)

Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».

KE = 7 см

P_EKFM = 4 · KE
P_EKFM = 4 · 7 = 28 (см)

Как найти периметр многоугольника

Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.

P_ABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)

Источник

Наименьший периметр многоугольника через площадь

Наверное часть из вас, знает легенду о возникновении города Карфаген.

В этой красивой легенде, есть математическая часть, которую не все замечают.

Каким образом царица должна разместить разрезанные полосы, что бы получить максимальную площадь?

Прямоугольник? Квадрат? Многоугольник?

В общем случае, задача совсем нетривиальная и ей посвящены работы серъезных ученых..

Но если говорить о геометрических фигурах, не «прижатых» к побережью, то здесь проще.

Итак задача формулируется так: Какая из геометрических фигур при одинаковой площади S имеет наименьший периметр P?

Рассматриваем только правильные геометрические фигуры, которые имеют одинаковые стороны.

Общая формула связывающая количество сторон (n) многоугольника, длину стороны (a) с площадью (S) выглядит вот так

тогда периметр (P) будет находится как

Для четырехугольника (квадрата)

Как видно при постоянной площади, минимальный периметр будет у шестиугольника. Конечно, если будем сравнивать 6-ти угольник с 12-ти угольников то 12 угольник выиграет по минимальному преиметру.

И естественно что лидером будет простая окружность которая является такой геометрической фигурой у которой при той же самой площади, периметр будет минимальным.

В природе однако встречаются чаще всего шестиугольники. Это строение глаз (фасетки) насекомых, это и строительство сот у пчёл, и еще много чего имеет шестиугольную форму.

Почему так? Просто шестиугольник обладает еще одним преимуществом, с помощью которого можно закрыть любую площадь с минимальными «потерями» — пустым местом между ячейками.

Посмотрите на игру «Мозаика». Какую форму имеют детали игры?

Поэтому шестиугольник так распространен в природе.

— закрывает всю площадь

— для строительтсва такой «соты» необходимо потратить минимальное количество материала, по сравнению например с треугольной или квадратной формой.

Источник

Как найти периметр фигуры

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение периметра

Периметр — это сумма длин всех сторон многоугольника.

Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.

Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.

Формулы нахождения периметра

Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.

Равносторонний многоугольник

У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.

P = 3 ⋅ a, где a — длина стороны.

Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.

А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.

Прямоугольник и параллелограмм

У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.

P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

Окружность

У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.

L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?

• Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
• Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
• Далее подставляем известные данные в формулу: (10 + 8) × 2 = 36 см;

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

• Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
• Известно, что равнобедренный треугольник имеет две равные стороны;
• Далее делим получившуюся сумму на два: 34 : 2 = 17 см;

Ответ: две другие стороны равны по 17 см.

Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.

• Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
• Длина окружности равна π × 2 × 20 = 40π см;

Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!

Источник

Что значит наименьший периметр

Слово «изопериметрический» происходит от слов «изос» (по-гречески «равный») и «периметр». Изопериметрическая задача (на плоскости) состоит в нахождении фигуры, имеющей наибольшую площадь среди всех фигур с одним и тем же периметром. Решение изопериметрической задачи является также решением и другой задачи, а именно: найти фигуру наименьшего периметра среди всех равновеликих фигур.

В самом деле, пусть среди фигур, имеющих периметр наибольшая площадь – у фигуры и эта площадь равна Рассмотрим произвольную другую фигуру той же площади. Пусть ее периметр равен Рассмотрим подобную ей фигуру с периметром Площади фигур и относятся так же, как квадраты периметров, то есть как к , поэтому площадь фигуры равна Поскольку ее периметр, по предположению, равен ее площадь меньше, чем у фигуры то есть меньше А значит, откуда Получается, что фигура имеет меньший периметр, чем любая другая равновеликая ей фигура.

Вообще, поскольку у подобных фигур площади пропорциональны квадратам периметров, у всех них одинакова величина 2 , а у фигур разной формы эта величина может отличаться. У фигур, представляющих решение изопериметрической задачи (независимо от размера), величина 2 должна быть наибольшей.
(В дальнейшем будем называть эту величину изопериметрическим частным ).

Заметим, что задача о наименьшей площади фигур с одним и тем же периметром особого смысла не имеет: например, при данном периметре можно делать все меньше и меньше одну из сторон прямоугольника (), другая же его сторона, равная (/2 – ), ограничена сверху величиной /2, а значит, площадь этой фигуры будет не больше /2. Даже если, например, = 1 000 000 км, можно сделать площадь 2 , если положить = 2∙10 –8 мм; если надо получить еще в 1000 раз меньшую площадь, надо и уменьшить в 1000 раз, и т. д. Таким образом, минимальной площади при данном периоде не существует: площадь может сколь угодно мало отличаться от нуля.

По аналогии с указанной изопериметрической задачей на плоскости можно рассмотреть и пространственную изопериметрическую задачу: какое трехмерное тело среди всех тел той же площади поверхности имеет наибольший объем. Уже древнегреческим математикам был известен ответ в изопериметрической задаче: в плоском случае искомая фигура – это круг (а в пространственном – шар). На эту мысль, наводит, во-первых, непосредственное сравнение площадей некоторых фигур равного периметра (или равной площади поверхности). Посмотрите на зависимость изопериметрического частного от формы плоских фигур.

Во-вторых, некоторые физические соображения также показывают, что ответ в изопериметрической задаче – это круг или шар. Например, капельки воды и мыльные пузыри не случайно имеют форму шара: силы поверхностного натяжения действуют так, чтобы уменьшать площадь поверхности. Характерно также, что кошки, когда холодно, спят, максимально сворачиваясь в клубок: так они уменьшают площадь поверхности тела, поскольку, чем меньше поверхность, тем меньше тепла они расходуют во внешнее пространство.

В третьих, древние греки считали круг наиболее совершенной фигурой (она максимально симметрична, именно такую форму имеют небесные тела и их орбиты). Это соображение увеличивало их уверенность в том, что именно круг, помимо других своих интересных свойств, должен также быть решением изопериметрической задачи.

Но вот геометрически древние греки доказать этого не могли, хотя и пришли к ряду частных, но важных результатов на эту тему, в том числе, в решении разнообразных задач о том, у какой фигуры определенного типа с заданными условиями площадь имеет наибольшее значение. Исследования такого рода имели не только теоретическое, но и практическое значение: при разделе земли в древности иногда совершались махинации, связанные с выдачей кусков большого периметра и маленькой площади; периметр легче измерить, чем площадь, поэтому некоторые доверчивые клиенты судили о величине участка земли по периметру.

Наверное, один из самых простых результатов на тему изопериметрических фигур – теорема о том, что из всех прямоугольников одинакового периметра наибольшую площадь имеет квадрат. В самом деле, пусть периметр всех рассматриваемых прямоугольников равен 4, а у данного прямоугольника две большие стороны равны каждая, а две меньшие, соответственно, каждая. Тогда площадь прямоугольника равна , то есть она не меньше 2 и достигает своего наибольшего значения тогда, когда прямоугольник является квадратом со стороной .

В «Началах» Евклида имеется единственная задача на максимум площади. Требуется в данный треугольник вписать параллелограмм наибольшей площади. Попробуйте экспериментальным путем найти искомый параллелограмм.

Ответ в этой задаче таков: параллелограмм имеет наибольшую площадь, когда точка делит сторону пополам. Евклид доказывает этот результат с помощью подобия треугольников. На первый взгляд кажется, что данная задача не имеет большого отношения к изопериметрическим задачам: в самом деле, периметры рассматриваемых параллелограммов не равны друг другу. Тем не менее, если «сдвинуть» вершину параллельно стороне , то площади параллелограмма и треугольников , и не изменятся (потому что не изменятся их высоты и основания). Задача при этом сводится к такой: в данный прямоугольный треугольник вписать прямоугольник наибольшей площади.

Далее: если пропорционально сжать или растянуть этот прямоугольный треугольник вдоль одного из катетов так, чтобы катеты стали равны, то высоты данных прямоугольника и треугольников изменятся в одном и том же отношении, а задача примет следующий вид: в данный прямоугольный равнобедренный треугольник вписать прямоугольник наибольшей площади.

Это задача вполне изопериметрическая: нетрудно видеть, что все рассматриваемые прямоугольники имеют один и тот же периметр – насколько увеличивается одна сторона, настолько уменьшается другая. Но решение изопериметрической задачи для прямоугольников мы уже знаем, это квадрат, а его вершина делит гипотенузу равнобедренного прямоугольного треугольника пополам. Значит, и в исходной задаче вершина искомого параллелограмма делит соответствующую сторону треугольника пополам.

Зенодор (II в. до н. э.) написал целый трактат «Об изопериметрических фигурах». Хотя трактат Зенодора не сохранился, некоторые его результаты дошли до нас в изложении математиков Паппа (III в. н. э.) и Теона (IV в. н. э.), в том числе следующие теоремы:

из двух треугольников с общей стороной и равными периметрами меньше площадь того, которому принадлежит наибольший из четырех углов, прилежащих к этой стороне (отсюда сразу следует, что из всех треугольников равного периметра, имеющих общее основание, площадь максимальна у равнобедренного треугольника);

при одинаковом числе сторон и равных периметрах площадь правильного многоугольника больше, чем неправильного;

из двух правильных многоугольников с равными периметрами больше площадь того, у которого больше сторон.

Таким образом, чем «ближе» многоугольник к кругу, тем, действительно, больше его изопериметрическое частное.

Нельзя не упомянуть об очень древней задаче, известной как задача Дидоны. Согласно древнему мифу, воспроизведенному в поэме Вергилия «Энеида», будущая основательница Карфагена – Дидона (вероятно, IX в. до н. э.) – бежала от преследований своего брата, тирана финикийского города Тир, на корабле с небольшим отрядом преданных ей людей. Они высадились на североафриканском побережье, принесли богатые подарки местному царю и попросили о выделении им участка; царь согласился отдать лишь «столько земли, сколько занимает воловья шкура». Тогда Дидона сделала из шкуры длинный тонкий ремень и огородила им значительную территорию на берегу моря, где и возник город Карфаген. Задачей Дидоны традиционно называется задача о том, какую форму должен иметь этот участок, чтобы занять наибольшую территорию при заданной длине ремня. Рассмотрим эту задачу для случая, когда берег прямолинеен. Пусть ремень имеет длину и опоясывает некую фигуру Ф₁. Отразим ее относительно берега. Тогда ремень и его отражение вместе являются границей (длины 2) новой фигуры Ф₂, составленной из фигуры Ф₁ и ее отражения. Если решение изопериметрической задачи – круг, то площадь Ф₂ (при данном периметре 2) максимальна, когда Ф₂ – круг. Но поскольку площадь Ф₂ ровно в 2 раза больше, чем у Ф₁, площадь Ф₁ тоже максимальна, если Ф₂ – круг, а ремень, соответственно, образует полуокружность.

Источник

Adblock
detector

Увидев этот вопрос, мы с сыном, который перешёл в пятый класс, улыбнулись, и начали вспоминать, когда же нахождение периметра проходили в школе. После небольшой, но оживлённой дискуссии, я решил этот вопрос, пробежав программу по математике в начальной школе на сайте Министерства образования и науки Украины. Как оказалось, мой мальчик был прав, что ещё во 2-ом классе, а не в 3-ем, как запомнилось мне, детям уже даются основы геометрический знаний.

Итак, квадрат – это плоская геометрическая фигура состоящая из четырёх отрезков, каждый из которых пересекается с двумя другими под углом в 90 градусов. Соответственно стороны данного четырёхугольника равны.

Для того же, чтобы узнать периметр (сумму всех сторон), достаточно измерить длину одного из отрезков и полученную величину умножить на 4.

Для наглядности проиллюстрирую ниже.

Как видите, всё довольно просто ! Успехов в учёбе !

Определение квадрата

Квадрат — это геометрическая фигура, правильный четырехугольник, у которого все углы и стороны равны.

Онлайн-калькулятор периметра квадрата

Противоположные стороны квадрата параллельны.

Другими словами, квадрат — это прямоугольник, у которого все стороны равны, или квадрат — это ромб, у которого все углы прямые. Квадрат имеет две диагонали, которые делятся точкой их пересечения пополам. Диагонали квадрата также делят его углы пополам и соединяют несмежные вершины.

Формула периметра квадрата

Для того чтобы найти периметр квадрата, нужно сложить длины всех его сторон.

Периметр квадрата

P=a+a+a+a=4⋅aP=a+a+a+a=4cdot a

aa — длина стороны квадрата.

Разберем задачу на нахождение периметра квадрата.

Задача

Найти периметр квадрата со стороной 12 см.

Решение

a=12a=12

Воспользуемся формулой нахождения периметра квадрата и подставим вместо aa его численное значение:
P=4⋅a=4⋅12=48P=4cdot a=4cdot 12=48 см.

Ответ: 48 см.

Ищете, где заказать решение контрольной работы? Эксперты Студворк с радостью помогут вам!

Тест по теме «Периметр квадрата»

Как найти периметр квадрата

О чем эта статья:

2 класс, 3 класс

Основные определения

Квадратом принято называть правильный четырёхугольник, у которого равны все углы и стороны. Это частный случай прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов.

Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Формула нахождения периметра квадрата

Как находится периметр квадрата, всегда зависит от исходных данных. Рассмотрим две формулы, которые проходят 2 и 3 класс.

Если известна длина стороны

P = a + a + a + a, где a — сторона.

Так как все стороны фигуры равны, можно использовать формулу в таком виде: P = 4 * a

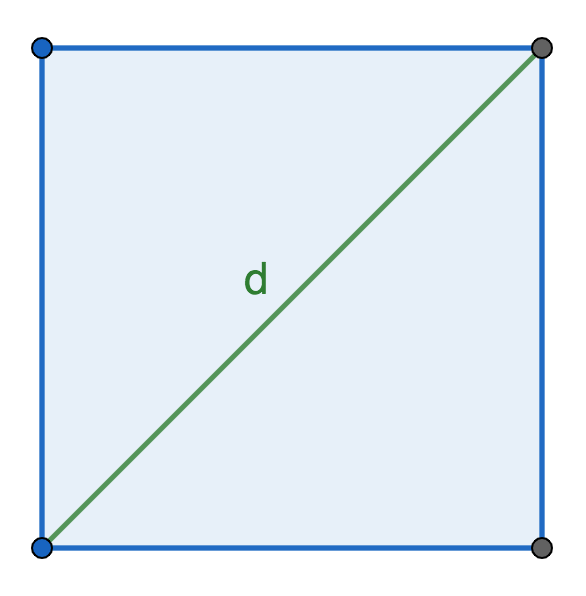
Если известна длина диагонали

P = d * 2 * √2, где d — диагональ.

Диагональ — это отрезок, который соединяет противоположные стороны фигуры.

Математика, как и любой другой предмет не сразу дается легко. Сложности могут возникать из-за неумения быстро делать простые арифметические действия — именно поэтому полезно практиковаться в решении примеров, как можно чаще. Давайте сделаем это прямо сейчас!

Занимайся изучением математики онлайн! Курсы по математике для учеников с 1 по 11 классы!

Решение задач

1. Найти периметр квадрата, диагональ которого равняется √4 см.

• Воспользуемся формулой P = d * 2 * √2;
• P = √4 * 2 * √2;

2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах

• Воспользуемся формулой P = 4 * a;
• P = 4 * 97

3. Периметр квадрата 48 см. Чему равна его сторона?

• Воспользуемся формулой P = 4 * a;
• Значит a = P : 4;
• a = 48 : 4;

4. Периметр квадрата 20 см. Как найти его площадь?

• Воспользуемся формулой P = 4 * a;
• Тогда a = P : 4;
• a = 20 : 4 = 5 см;
• Воспользуемся формулой S = a * a;
• Значит S = 5 * 5;

Источник

Как найти периметр фигуры

О чем эта статья:

Определение периметра

Периметром принято называть длину всех сторон многоугольника. Какой буквой обозначается периметр — заглавной латинской P. Под обозначением «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Формула нахождения периметра

Рассмотрим пять фигур.

Треугольник

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три.

P = 3 * a, где a — длина стороны.

Квадрат и ромб

Периметр квадрата — это произведение длины стороны на четыре. Формула ромба выглядит идентично.

P = 4 * a, где a — длина стороны.

Прямоугольник и параллелограмм

Периметр прямоугольника — сумма длины и ширины, умноженная на два. Формула параллелограмма выглядит соответственно.

P = 2 * (a + b), где a — ширина, b — высота.

Записывайтесь на онлайн уроки по математике к лучшим преподавателям! Уроки для учеников с 1 по 11 классы!

Равнобедренная трапеция

Формула для равнобедренной трапеции отличается от прямоугольника тем, что у первого есть две равные стороны.

P = a + b + 2 * c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d * π = 2 * r * π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?

• Для использования формулы P = 2 * (a + b), нам нужно найти ширину;
• Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
• Далее подставляем известные переменные в формулу: (10 + 8) * 2 = 36 см;

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

• Используя формулу P = a + b + c вычислим сумму двух неизвестных сторон: 40 — 6 = 34 см;
• Известно, что равнобедренный треугольник имеет две равные стороны;
• Далее делим получившуюся сумму на два: 34 : 2 = 17 см;

Ответ: две другие стороны равны 17см.

Круг вписан в квадрат, его сторона равна 20 см. Найти периметр круга.

• Периметр круга равен длине ограничивающей его окружности. Значит P = L = d * π;
• Сторона квадрата для круга является диаметром, поэтому P = 20 * 3,14;

Источник

Нахождение периметра квадрата: формула и задачи

В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.

Формула вычисления периметра

По длине стороны

Периметр (P) квадрата равняется сумме длин его сторон.

P = a + a + a + a

Так как все стороны квадрата равны, формулу можно представить в виде произведения:

P = 4 ⋅ a

По длине диагонали

Периметр (P) квадрата равен произведению длины его диагонали на число 2√ 2 :

P = d ⋅ 2√ 2

Данная формула следует из соотношения длин стороны (a) и диагонали (d) квадрата:
d = a√ 2 .

Примеры задач

Задание 1
Найдите периметр квадрата, если его сторона равна 6 см.

Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.

Задание 2
Найдите периметр квадрата, диагональ которого равняется √ 2 см.

Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √ 2 см ⋅ 2√ 2 = 4 см.

Решение 2:
Выразим длину стороны через диагональ:
a = d / √ 2 = √ 2 см / √ 2 = 1 см.

Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.

Источник

Периметр квадрата

Периметр квадрата? как найти периметр квадрата, примеры, формула периметра квадрата.

О периметре квадрата.

Формула периметра квадрата

Интересный поисковый запрос — «что такое периметр квадрата«.

Что такое периметр квадрата

Слово периметр пришло из древности и например древние-греческом обозначала окружность(περίμετρον).

Или если совсем по простому — периметр квадрата это — сумма всех границ.

Периметр квадрата это сумма всех сторон квадрата, поскольку их 4 одинаковых, то одну сторону, надо умножить на 4.

Формула периметра квадрата — периметр квадрата равен стороне умноженной на 4 -> P=4a

Где P — периметр квадрата,

a — длина одной из сторон.

Как найти периметр квадрата. если известна сторона!?

Как мы уже говорили выше у нас есть формула нахождения периметра :

найдите периметр квадрата, если сторона квадрата равна 12 см.

Сторона квадрата это а, она равна 12см.

Подставляем 12 в формулу вместо буквы «а».

P = 4a -> P = 4 * 12-> P = 48см.

Если сторона квадрата равна 12 см, то периметр квадрата равен 48см.

Как найти периметр квадрата. если известна площадь!?

найдите периметр квадрата, если площадь квадрата равна 25см².

Опять вспоминаем формулу площади квадрата :

Из этой формулы нам требуется вывести сторону :

Далее берем формулу периметра квадрата и заменяем сторону на корень квадратный.

Извлекаем корень из 25 на калькуляторе

После этого умножаем на 4 :

Если площадь квадрата 25см², то периметр будет равен 20см.

Источник

Как найти периметр квадрата

Что такое периметр квадрата

Квадрат — это правильный четырехугольник, все его стороны и углы равны.

Про него также говорят, что это частный случай прямоугольника или ромба.

Периметр квадрата — это сумма длин всех его сторон или произведение одной его стороны на 4.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Способы вычисления

Для вычисления периметра квадрата применяется несколько видов несложных формул.

По длине стороны

Самый простой способ, если известна величина одной из его сторон. Сразу вспоминаем, что мы имеем дело с правильным четырехугольником, и подставляем значение в уравнение:

где (a) — это сторона фигуры.

По длине диагонали

Если известна только диагональ правильного прямоугольника, формула для нахождения суммы всех его ребер будет выглядеть так:

что следует из соотношения длин стороны и диагонали (d=asqrt2)

По площади

Зная площадь фигуры, найти ее периметр можно так:

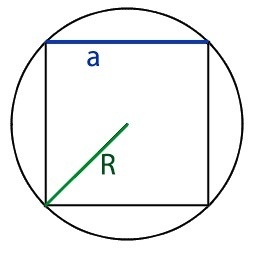
По радиусу описанной окружности

Радиус описанной вокруг квадрата окружности — это половина его диагонали. Формула для нахождения P в данном случае:

где R — радиус данной окружности.

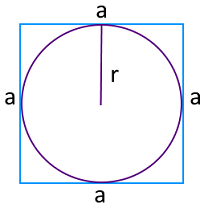
По радиусу вписанной окружности

Радиус вписанной окружности — это половина величины ребра правильного прямоугольника. Таким образом, уравнение для нахождения P выглядит так:

где r — радиус вписанной окружности.

Найти P квадрата, если его ребро a равно 5 см.

Так как P = 4a, подставляем сюда известное значение, и получается (P = 4times5= 20 см.)

Узнать P правильного четырехугольника, если его диагональ d равна 6 см.

Используем формулу (P;=;2dsqrt2) и подставляем известное значение. Получается: (P = 2 * 6sqrt2 = 12sqrt2 см.)

Ответ: (12sqrt2 см.)

Площадь квадрата равна 16 см². Каков периметр?

Мы знаем, что (P;=;4sqrt S\) . Значит, подставляя значение в формулу (P;=;4sqrt S\) , мы имеем: (P;=;4sqrt 16 = 4times4 = 16) см.

Известно, что 1/2 диагонали правильного прямоугольника составляет (9sqrt2\ ) см. Вычислить P.

1/2 диагонали имеющейся фигуры — это как раз радиус описанной окружности. Подставляем значение в уравнение (P;=;4Rsqrt2\) . Получается: (P;=;4Rsqrt2 = 4times9sqrt2timessqrt2 = 72) см.

Дан квадрат и вписанная в него окружность. Половина стороны a фигуры равна 7 см, посчитать P.

Так как половина стороны данной фигуры — это радиус вписанной в нее окружности. Используем метод нахождения по радиусу вписанной окружности: (P;=;8r\) . Подставляем известное значение: (P;=;8r = 8times7 = 56 см.)

Источник