ВИДЕО УРОК
Периодические функции.
Функцию у = f(х), х ∈ Х, называют периодической,
если существует такое отличное от нуля число
Т, что для любого х из области определения функции справедливо
равенство:
f(х + Т) = f(х) = f(х – Т).
Число Т называют периодом функции у = f(х).
Из этого
определения сразу следует, что если Т –
период функции
у = f(х), то
2Т, 3Т, 4Т, –Т, –2Т, –3Т,
–4Т
– также периоды
функций. Значит у периодической функции бесконечно много периодов.
Если Т – период функции, то число вида kТ,
где k – любое целое
число, также является периодом функции.
Чаще всего (но не
всегда) среди множества положительных периодов функции можно найти наименьший.
Его называют основным периодом.
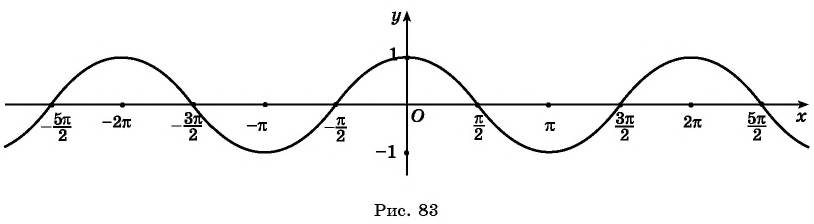
График периодической
функции состоит из неограниченно повторяющихся одинаковых фрагментов.
График каждой
периодической функции состоит из одинаковых линий повторяющихся и изолированных
друг от друга, как в рассматриваемом случае, или соединенных в одну общую линию
(синусоида и другие.)
Графики
периодических функций обладают следующей особенностью. Если Т – основной период функции у = f(х), то для построения её графика достаточно построить ветвь
графика на одном из промежутков оси х длиной
Т, а затем осуществить параллельный перенос этой ветви по
оси х на
± Т, ±
2Т, ± 3Т, …
Чаще всего в
качестве такого промежутка длиной Т выбирают промежуток с концами в точках
(–Т/2; 0) и (Т/2; 0) или
(0; 0) и (Т; 0).
ПРИМЕР:
Рассмотрим функцию
у = х – [х], где [х] – целая часть числа. Если к
произвольному значение аргумента этой функции добавить 1, то значение функции от этого не изменится:
f(x + 1) = (x
+1) – [x + 1] = x + 1 – [x] – 1
= x – [x] = f (x).
Следовательно, при любом
значении х
f(x + 1) = f(x).
А это значит, что рассматриваемая функция
периодическая, период которой равен 1. Любое целое число
также является периодом данной функции, но обычно рассматривают только
маленький положительный период функции.
График этой функции
приведен на рисунке. Он состоит из бесконечного множества равных отрезков, которые
повторяются.
Периодичность тригонометрических функций.
Возьмём произвольный угол α и построим
подвижной радиус ОМ единичной окружности такой, что угол,
составленный с осью Ох этим радиусом, равен α.
Если мы к углу прибавим
2π или 360° (то есть полный
оборот), то углу α + 2π или α + 360° будет соответствовать то же положение
подвижного радиуса ОМ, что для угла α.
Так как синус и косинус угла,
составленного с осью Ох подвижным радиусом ОМ единичной
окружности, по сути соответственно ордината
у и
абсцисса х точки М, то
sin (α + 2π) = sin α или
sin (α + 360°) = sin α
и
cos (α + 2π)
= cos α или
cos (α + 360°) = cos α.
Таким образом, функции sin α и cos α от
прибавления к аргументу α одного
полного оборота (2π или 360°) не меняют своих значений.
Точно так же, прибавляя к
углу α любое целое
число полных оборотов, мы не изменим положения подвижного радиуса ОМ, а потому:
sin (α + 2kπ) = sin α или
sin (α + 360°k) = sin α
и
cos (α + 2kπ) = cos α или
cos (α + 360°k) = cos α,
где k – любое целое
число.
Функции, обладающие таким
свойством, что их значения не изменяются от прибавления к любому допустимому
значению аргумента определённого постоянного числа, называются периодическими.
Следовательно, функции sin α и cos α – периодические.
Наименьшее положительное число,
от прибавления которого к любому допустимому значению аргумента не изменяется
значение функции, называется периодом функции.
Периодом функции sin α и cos α
является 2π или 360°.
Функции tg α и сtg α также
периодические и их периодом является число
π или 180°.
В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным
радиусом ОМ единичной окружности.
Построим точку М‘,
симметричную точке М относительно
начала координат. Один из углов, образованных с осью Ох подвижным
радиусом ОМ‘, будет равен α + π.
Если х и у – координаты точки
М, то точки М‘ будут –х и –у. Поэтому
sin α = у, cos α = х,
sin (α + π) = –у,
cos (α + π) = –х.
Отсюда
и, следовательно,
tg (α + π) = tg α,
сtg (α + π)
= сtg α.
отсюда следует, что значения tg α и сtg α не
изменяются, если к углу α прибавить любое число полуоборотов:
tg (α + kπ) = tg α,
сtg (α + kπ) = сtg α.
где k – любое целое
число.
Периоды функций
y = A sin (ωx + φ) и
y = A cos (ωx + φ)
вычисляются по формуле
T = 2π/ω,
а период функции
y = A tg (ωx + φ)
по формуле
T = π/ω.
Если период функции y = f(x) равен T1, а период функции y = g(x) равен T2, то период функций
y = f(x) + g(x) и
y = f(x) – g(x)
равен наименьшему числу, при делении которого
на T1 и T2 получаются целые числа.
ПРИМЕР:
Найти
период функции
y = 3 sin (x – 2) + 7 соs πx.
РЕШЕНИЕ:
Период
функции
y = 3 sin (x – 2)
равен
T1 = 2π/1 = 2π.
Период
функции
y = 7 соs πx
равен
T2 = 2π/π = 2.
Периода
у функции
y = 3 sin (x – 2) + 7 соs πx
не
существует, так как такого числа, при делении которого на 2π и
на 2 получались бы целые числа, нет.
ОТВЕТ:
Периода
не существует.
ПРИМЕР:
Доказать
следующее утверждение:
tg
3850° = tg 250°.
РЕШЕНИЕ:
Так как тангенс – периодическая функция с минимальным
периодом 20 ∙ 180°, то получим:
tg
3850° = tg (20 ∙ 180° + 250°) = tg 250°.
ПРИМЕР:
Доказать
следующее утверждение:
сos (–13π) = –1.
РЕШЕНИЕ:
Так как косинус – чётная и периодическая функция с
минимальным периодом 2π, то получим:
сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.
ПРИМЕР:
Доказать
следующее утверждение:
sin (–7210°) = – sin 10°.
РЕШЕНИЕ:
Так как синус – нечётная и периодическая функция с
минимальным периодом 20 ∙ 360°, то получим:
sin (–7210°) = –sin 7210° = –sin (20 ∙ 360° + 10°) – sin 10°.
ПРИМЕР:
Найти основной период функции
sin 7х.
РЕШЕНИЕ:
Пусть Т основной период функции, тогда:
sin 7х = sin 7(х + t) = sin (7х + 7t)
так как 2πk период синуса, то получим:
sin (7х + 7t) = sin (7х + 2πk),
ОТВЕТ:
ПРИМЕР:
Найти основной период функции
соs 0,3х.
РЕШЕНИЕ:
Пусть Т основной период функции, тогда:
соs 0,3х = соs 0,3(х + t)
= соs (0,3х + 0,3t)
так как 2πk период косинуса, то получим:
соs (0,3х + 0,3t) = соs (0,3х + 2πk),
ОТВЕТ:
ПРИМЕР:
Найти период функции:
y = 5sin 2x + 2ctg 3х.
РЕШЕНИЕ:
Период функции
y = 5sin 2x
равен Т1 = 2𝜋/2 = π,
а период функции
y = 2ctg 3х
равен Т2 = 𝜋/3.
Наименьшее число, при делении которого на
Т1 = π и Т2 = 𝜋/3
– получаются целые числа будет число π.
Следовательно, период заданной функции равен Т = π.
ПРИМЕР:
Найти период функции:
y = 9sin (5x + π/3) – 4cоs (7х + 2).
РЕШЕНИЕ:
Находим периоды слагаемых. Период функции
y = 9sin (5x + π/3)
равен Т1 = 2𝜋/5,
а период функции
y = 4cоs (7х + 2)
равен Т2 = 2𝜋/7.
Очевидно, что период заданной функции равен
Т = 2π.
ПРИМЕР:
Найти период функции:
y = 3sin πx + 8tg (х + 5).
РЕШЕНИЕ:
Период функции
y = 3sin πx
равен Т1 = 2π/π = 2,
а период функции
y = 8tg (х + 5)
равен Т2 = 𝜋/1 = π.
Периода у заданной функции не существует, так как нет
такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.
ПРИМЕР:
Найти период функции:
y = sin 3x + соs 5х.
РЕШЕНИЕ:
Период функции
y = sin 3x
равен Т1 = 2π/3,
а период функции
y = соs 5х
равен Т2 = 2π/5.
Приведём к общему знаменателю периоды:
Т1 = 10π/15, Т2 = 6π/15.
Тогда наименьшее общее кратное (НОК) будет:
НОК (10π; 6π)
= 30π.
Теперь найдём период заданной функции:
Т = 30π/15 = 2π.
Задания к уроку 5
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований
Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции
где T — период функции y=f(x). Эта формула позволяет быстро найти период тригонометрических функций такого вида. Для функций y=sin x и y=cos x наименьший положительный период T=2п, для y=tg x и y=ctg x T=п. Рассмотрим на конкретных примерах, как найти период функции, используя данную формулу.
Найти период функции:
1) y=5sin(3x-п/8).
Здесь А=5, k=3, b=-п/8. Для нахождения периода нам нужно только k — число, стоящее перед иксом. Поскольку период синуса T=2п, то период данной функции
А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то
А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции
А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть
Преподаватель который помогает студентам и школьникам в учёбе.
Содержание:
Некоторые свойства функции
Например, областью определения функции 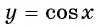
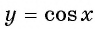
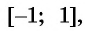
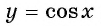
Определение функции y=cos x
Определение:
Зависимость, при которой каждому действительному числу 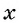
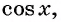
Свойства функции y=cos x
Свойства функции 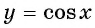
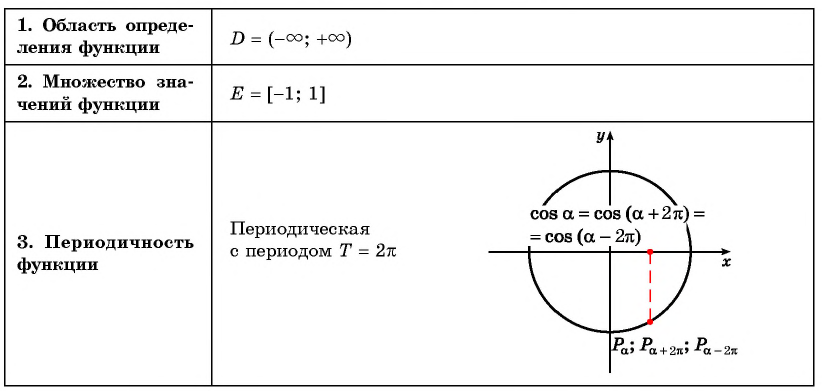
График функции y=cos x
График функции 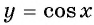
Пример №1
Определите, какие из данных точек принадлежат графику функции
Решение:
а) Подставим в формулу 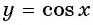
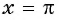
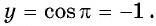
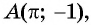
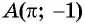
б) При 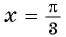
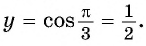
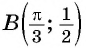
в) При 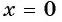
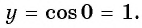
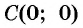
г) При 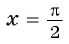
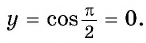
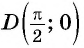
Пример №2
Найдите область определения и множество значений функции
Решение:
Областью определения функции является множество всех действительных чисел, т. е.
Множеством значений функции 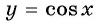
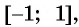
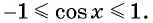
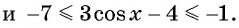
Пример №3
Найдите наименьшее значение функции
Решение:
Так как 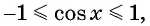
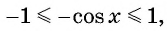
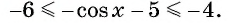
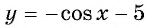
Пример №4
Используя свойство периодичности функции 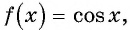
Решение:
Так как число 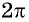
- Заказать решение задач по высшей математике
Пример №5
Используя свойство четности функции 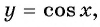
Решение:
Так как функция 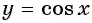
Тогда:
Пример №6
Исследуйте функцию на четность (нечетность):
Решение:
а) 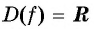
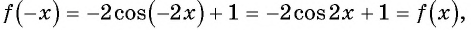
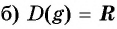
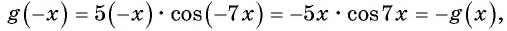
Пример №7
Найдите нули функции:
Решение:
а) Пусть 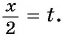
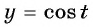
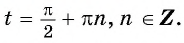
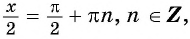
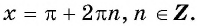
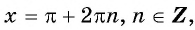
б) Пусть 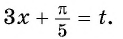
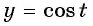
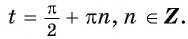
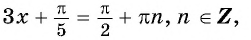
Таким образом, числа 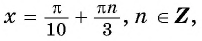
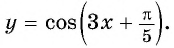
Пример №8
Определите знак произведения
Решение:
Так как 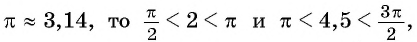
4,5 радиана и 2 радиана принадлежат промежутку 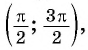
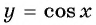
Угол 7 радиан принадлежит промежутку, на котором функция 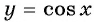
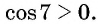
Пример №9
Что больше:
Решение:
Так как функция 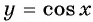
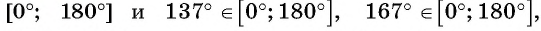
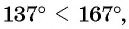
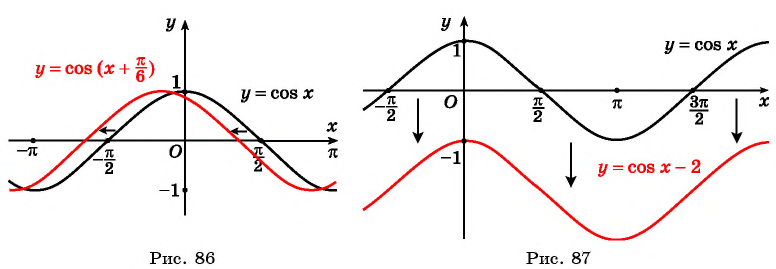
Пример №10
Постройте график функции:
Решение:
а) График функции 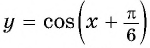
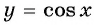
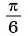
б) График функции 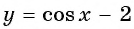
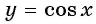
- Функции y=tg x и y=ctg x – их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
§ 13. Свойства тригонометрических функций
Объяснение и обоснование
1. Знаки тригонометрических функций легко определить, исходя из опреде –
ления этих функций.
Например,
— это ордината соответствующей точки
единичной
окружности. Поэтому значение будет положительным, если точка
имеет положительную ординату, a это будет тогда, когда точка находит-
ся в I или II четверти (рис. 67). . Если точка находится в III или IV чет –
верти, то ее ордината отрицательна, и поэтому тоже отрицателен.
Аналогично, учитывая, что — это абсцисса соответствующей точки
,
получаем, что >0 в I и IV четвертях (абсцисса точки
положительна)
и <0 во II и III четвертях (абсцисса точки
отрицательна) (рис. 68).
Поскольку там, где
и
имеют одинаковые знаки, то есть в I и III четвертях,
и там, где
и
имеют разные знаки, то есть во II и IV чет –
вертях (рис. 69).
2. Четность и нечетность тригонометрических функций.
Чтобы исследовать тригонометрические функции на четность и нечет –
ность, заметим, что на единичной окружности точки и
расположе-
ны симметрично относительно оси Ox (рис. 70). Следовательно, эти точки
имеют одинаковые абсциссы и противоположные ординаты.
Тогда
Таким образом, — четная функция, а
— нечетная.
Поэтому — нечетные функции.
Замечание. Приведенное исследование четности и нечетности функ –
ций и
неявно опирается на утверждение, что точки
и
будут расположены симметрично относительно оси Ох при любом значе –
нии Приведем план возможного обоснования этого утверждения.
1) Если или
то утверждение очевидно в силу сим –
метрии единичной окружности относительно оси Ох, проходящей через
центр окружности.
2) В силу этой же симметрии утверждение очевидно и при или
3) Для всех других значений угла используем утверждение (которое мы
примем без доказательства), что его радианную меру α можно записать
в виде (радиан) удовлетворяет неравенству
и, учитывая, что на единичной окружности углам
и
соответствует одна и та же точка, сводим
этот случай к случаю 2.
Четность и нечетность тригонометрических функций можно применять
для вычисления значений тригонометрических функций отрицательных
углов (чисел).
Например,
3. Периодичность тригонометрических функций. Множество процессов и яв-
лений, которые происходят в природе и технике, имеют повторяющийся
характер (например, движение Земли вокруг Солнца, движение маховика).
Для описания процессов такого рода используют так называемые периоди –
периодические функции.
Функция y = f (x) называется периодической с периодом T ≠ 0, если для
любого x из области определения функции числа (x + T) и (x – T) также
f (x + T) = f (x).
Из приведенного определения получаем, что f (x – T) = f ((x – T) + T) =
= f (x), то есть, если T — период функции f (x), то и – T тоже период этой
функции. Также можно доказать, что ±2Т, ±3Т, …, ±kТ — тоже периоды
этой функции (k ∈ N).
Учитывая, что на единичной окружности числам (углам)
где
соответствует одна и та же точка (рис. 71), получаем:
Тогда является периодом функций
и
.
При k = 1 получаем, что — это период функций
и
.
Докажем, что эти функции не могут иметь меньший положительный пе-
риод. Чтобы доказать, что — наименьший положительный период
косинуса, допустим, что T > 0 — период функции . Тогда для лю –
бого значения x выполняется равенство cos (x + T) = cos x. Взяв x = 0,
получаем cos T = 1. Но это означает, что на единичной окружности при
повороте на угол T точка снова попадает в точку
, то есть
,
где k ∈ Z. Таким образом, любой период косинуса должен быть кратным
, а значит,
— наименьший положительный период косинуса.
Чтобы обосновать, что
— наименьший положительный период
функции sin x, достаточно в равенстве sin (x + T) = sin x, которое выпол-
няется для любых значений x, взять . Получаем
Но это
означает, что при повороте на угол точка
попадает в точку A (0;1)
(рис. 71), то есть таким образом
. Следовательно,
любой период синуса должен быть кратным , а значитит,
— наименьший положительный период косинуса.
Если учесть, что на единичной окружности точки
и
являются
диаметрально противоположными, то этим точкам соответствует одна и та же
точка на линии тангенсов (рис. 72) или на линии котангенсов (рис. 73). Тогда
также
То есть периодом функций tg x и ctg x является (k ≠ 0, k ∈ Z).
Наименьшим положительным периодом для функций tg x и ctg x явля-
ется
Чтобы доказать это, достаточно в равенстве tg (x + T) = tg x взять x = 0.
Тогда получим tg T = 0. Таким образом, T =, где k ∈ Z. Итак, любой
период тангенса должен быть кратным а значит,
– наименьший по-
ложительный период тангенса. Аналогично в соответствующем равенстве
для ctg x достаточно взять .
Чтобы иметь представление о поведении графика периодической функ –
ции y = f (x), напомним, что по определению график функции y = f (x)
состоит из всех точек M координатной плоскости, которые имеют ко –
ординаты (x; y) = (x; f (x)). Первая координата для точек графика вы-
бирается произвольно из области определения функции. Выберем как
первую координату значение x + T (или в обобщенном виде — значение
x + kT при целом значении k) и учтем, что для периодической функции
f(x + T) = f(x – T) = f (x) (в общем случае f (x + kT) = f (x)). Тогда графи-
ку функции y = f (x) будет принадлежать также точка M1 координатной
плоскости с координатами:
(x + T; y) = (x + T; f (x + T)) = (x + T; f (x)).
Точку M1 (x + T; f (x)) можно получить из точки M (x; f (x)) параллель –
ным переносом вдоль оси Ox на T единиц (рис. 74). В общем случае точку
M2 (x + kT; f (x)) можно получить из точки M (x; f (x)) параллельным пе –
реносом вдоль оси Ox на kT единиц. Таким образом, через промежуток T
вид графика периодической функции будет повторяться. Поэтому для
построения графика периодической функции с периодом T достаточно
построить график на любом промежутке длиной T(например, на проме-
жутке [0;T]), а потом полученную линию параллельно перенести вправо
и влево вдоль оси Ox на расстояние kT, где k — любое натуральное число.
Примеры решения задач
Задача 1 Пользуясь периодичностью, четностью и нечетностью триго-
нометрических функций, найдите:
Задача 1 Докажите утверждение: если функция y = f (x) периодическая
с периодом T, то функция y = Af (kx + b) также периодическая
с периодом .png)
Используем утверждение, доказанное в задаче 2 для нахождения перио-
дов функций.
Например,
1) если функция sin x имеет период
, то функция sin 4x имеет период
2) если функция tg x имеет период
,то функция
имеет период
Вопросы для контроля
1. а) Назовите знаки тригонометрических функций в каждой из коорди –
натных четвертей.
б *) Обоснуйте знаки тригонометрических функций в каждой из коорди-
натных четвертей.
2. а) Какие из тригонометрических функций являются четными, а какие
нечетными? Приведите примеры использования четности и нечетности
для вычисления значений тригонометрических функций.
б *) Обоснуйте четность или нечетность соответствующих тригонометри-
ческих функций.
3. а) Какая функция называется периодической? Приведите примеры.
б *) Обоснуйте периодичность тригонометрических функций. Укажи-
те наименьший положительный период для синуса, косинуса, тангенса
и котангенса и обоснуйте, что в каждом случае этот период действитель-
но является наименьшим положительным периодом.
Упражнения
1. Пользуясь периодичностью, четностью и нечетностью тригонометриче-
ской функции, найдите:
1) 2) sin (–750°); 3)
4) ctg 945°;
5) 6) cos (–3630°); 7)
8) tg 600°.
2*. Среди данных функций найдите периодические и укажите наименьший
положительный период для каждой из них:
1) f(x)= x^2; 2) f(x)= sin 2x; 3) f(x)= | x |; 4) f(x)= tg 3x; 5)f(x) = 3.
3. Найдите период каждой из данных функций:
1) y= cos 2x; 2)y = tg 5x; 3) 4) y = ctg 3x; 5)
4. На каждом из рисунков 75–78 приведена часть графика некоторой перио-
дической функции с периодом T. Продолжите график на отрезке [–2T; 3T].
Четность, нечетность, периодичность тригонометрических функций
План урока
- Четность, нечетность тригонометрических функций;
- Исследование тригонометрических функций на четность, нечетность;
- Периодичность тригонометрических функций;
- Определение периода тригонометрических функций.
Цели урока
- Знать определение четности, нечетности, периодичности функций, в том числе тригонометрических функций;
- Уметь исследовать функцию на четность, нечетность, находить период тригонометрических функций.
Разминка
- Найти область определения функций y=4cosx-π3; y=tg x+2π7.
- Найти множество значений функции y=cos x-sin x2.
- Назовите формулы синуса, косинуса, тангенса, котангенса отрицательных аргументов.
- Что такое четная функция? Нечетная функция?
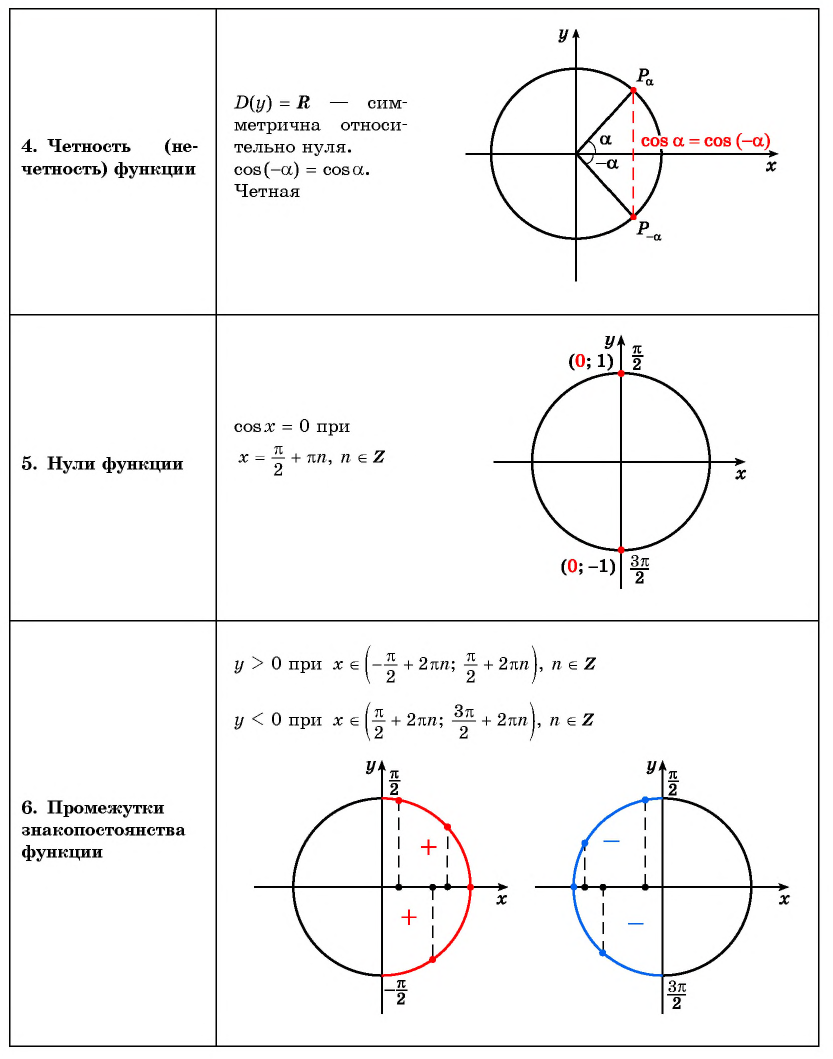
Четность, нечетность тригонометрических функций
В курсе основной школы были изучены такие понятия, как четность, нечетность функций. Напомним их.
Функция y=f(x) называется
четной
, если для каждого значения x из ее области определения выполняется равенство f(-x)=f(x).
Функция y=f(x) называется
нечетной
, если для каждого значения x из ее области определения выполняется равенство f(-x)=-f(x).
Областью определения функций y=sin x, y=cos x является множество R всех действительных чисел и кроме того для любого значения x справедливы равенства sin(-x)=-sin x, cos(-x)=cos x. Тогда функция y=sin x – нечетная функция, а y=cos x – четная. Областью определения функции y=tg x является множество всех действительных чисел, кроме x=π2+πn, n∈Z и в каждой точке области определения верно равенство tg(-x)=-tg x. Тогда функция y=tg x – нечетная. Аналогично рассуждая, получим, что на множестве R за исключением чисел x=πn, n∈Z функция y=ctg x – нечетная.
Выяснить, является ли четной, нечетной или не является ни четной, ни нечетной функция:
1) f(x)=3×4+3cos x;
2) f(x)=2sin x1+cos x.
Решение
1) Функция определена на множестве всех действительных чисел. Найдем f(-x) и сравним с f(x).
f-x=3-x4+3cos-x=3×4+3cos x=f(x).
Значит, данная функция является четной.
2) Область определения функции Df:1+cos x≠0, откуда x≠π+2πn, n∈Z.
f-x=2 sin-x1+cos-x=-2sin x1+cos x=-2 sin x1+cos x=-fx.
Функция f(x)=2sin x1+cos x – нечетная.
Ответ: 1) четная; 2) нечетная.
Выяснить, является ли четной, нечетной или не является ни четной, ни четной функция:
1) y=51-2sin x;
2) y=3+sin x-cos x.
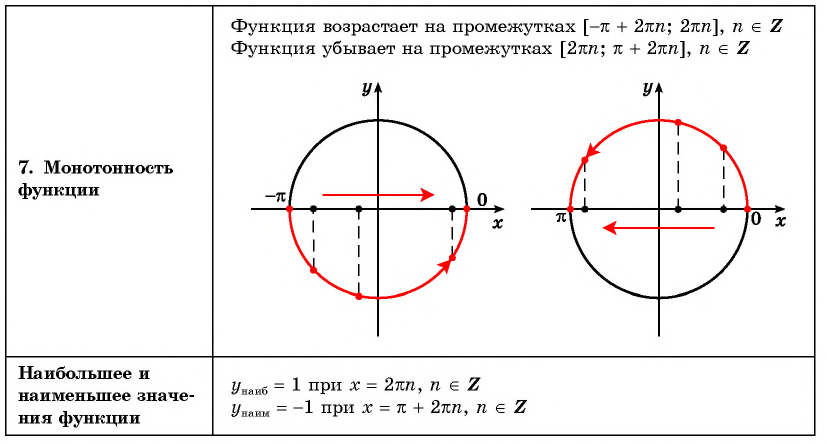
Известно, что для любого действительного x справедливы равенства sinx+2π=sin x, cosx+2π=cos x, т.е. если периодически изменять аргумент на 2π, то значения синуса и косинуса будут повторяться. Такие функции называются периодическими с периодом 2π.
Функция f(x) называется периодической, если существует такое ненулевое число T, что для любого x из области определения этой функции выполняется равенство fx-T=fx=fx+T. Число T называется периодом функции f(x).
Из определения следует, что если x принадлежит области определения fx, то и числа x-T, x+T (а вообще говоря, числа x+Tn, n∈Z) также принадлежат области определения этой периодической функции, fx+Tn=fx, n∈Z.
Функции y=tg x, y=ctg x являются периодическими с периодом T=π.
Докажите, что функция является периодической с периодом T.
1) f(x)=sin x2, T=4π;
2) f(x)=sin 2x+cosx, T=π.
Решение
1) Функция определена на всей числовой оси. Докажем, что для любого действительного числа x выполняется равенство fx+T=fx.
fx+4π=sinx+4π2=sinx2+2π=sin x2=fx.
Итак, равенство f(x+T)=f(x) выполняется для любого x из области определения. Аналогично f(x-T)=f(x). Значит, T=4π — период данной функции.
2) Для преобразования формулы, задающей функцию, воспользуемся формулой синуса двойного аргумента и вынесем общий множитель за скобки.
f(x)=cos x 2sin x+1.
Функция определена на всей числовой оси. Докажем выполнение равенства f(x+T)=f(x) для каждой точки области определения.
fx+π=cos x+π2 sinx+π+1=
=-cos x -2 sin x+1=cos x 2 sin x+1=f(x) .
Равенство fx+T=f(x) выполняется для любого x из области определения. Аналогично, f(x-T)=f(x), т.е. T=π – период данной функции.
Найти наименьший положительный период функции fx=sin 23 x.
Решение
Функция определена на всей числовой оси. Так как она периодическая, то для каждой точки области определения выполняется равенство fx+T=fx, т.е. sin23x+T=sin23x,
sin23x+23T=sin23x, отсюда 23T=2π, T=3π.
Ответ: 3π.
Чтобы лучше запомнить, какая из тригонометрических функций будет четной, какая – нечетной, а также наименьший положительный период, заполним следующую таблицу.
Таблица четности, нечетности, периодичности тригонометрических функций
|
Функция |
Четность, нечетность |
Наименьший |
|
y=sinx |
Нечетная |
2π |
|
y=cosx |
Четная |
2π |
|
y=tgx |
Нечетная |
π |
|
y=ctgx |
Нечетная |
π |
1. Доказать, что функция является периодической с периодом T.
1) y=sin34x, T=8π3;
2) y=sin 5x-cos 5x, T=2π5;
3) y=tg 3x-2π3, T=π3;
4) y=tg x, T=π.
2. Найти наименьший положительный период функций:
1) y=6-sin x;
2) y=cos 4x.
Контрольные вопросы
- Какие из тригонометрических функций являются четными? Нечетными?
- Назовите наименьший положительный период каждой тригонометрической функции.
Ответы
Упражнение 1
1. ни четная, ни нечетная;
2. ни четная, ни нечетная.
Упражнение 2
2. 1) 2π; 2) π2.












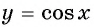
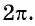
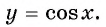
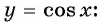

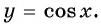
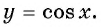
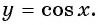
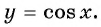
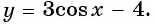
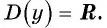
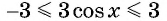
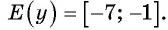
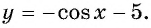
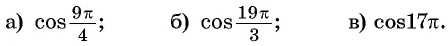
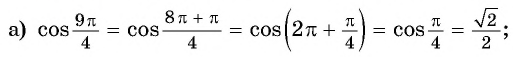

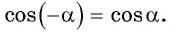

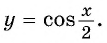
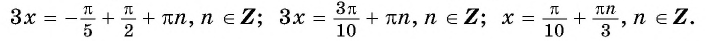
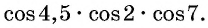
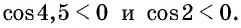
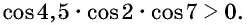
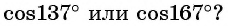
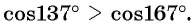


.jpg)


.png)
.png)
.png)
.png)
.png)
