Как найти наименьший положительный период функции sin

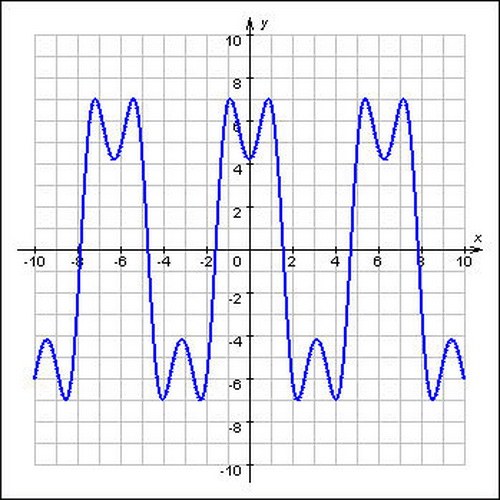
С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например,  — периодические функции.

Дадим определение периодической функции:

Функция называется периодической, если существует такое число , не равное нулю, что для любого из ее области определения

Другими словами, это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого фиксированного ненулевого числа . Число называется периодом функции. Как правило, говоря о периоде, мы имеем в виду наименьший положительный период функции.

Например, — периодические функции.

Для функций и период ,

Для функций и период

Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:

1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения

График функции может выглядеть, например, вот так:

Отметим точку М (1; 5), принадлежащую графику функции . Поскольку период функции равен 2, значения функции в точках будут также равны пяти. Здесь k — целое число.

Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.

Значения функции в точках -3 и 7 равны пяти. Мы получим:

2. График четной периодической функции совпадает с графиком функции  на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).

Построим график функции при

Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.

Период функции равен 2. Повторим периодически участок длины 2, который уже построен.

Найдем

3. Найдите наименьший положительный период функции

Наименьший положительный период функции равен

График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).

Значит, у функции частота в 3 раза больше, чем у функции , а наименьший положительный период в 3 раза меньше и равен . Значит, на отрезке укладывается ровно 3 полных волны функции

Рассуждая аналогично, получим, что для функции наименьший положительный период равен На отрезке укладывается ровно 5 полных волн функции

Числа 3 и 5 — взаимно простые. Поэтому наименьший положительный период функции равен .

4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции

По условию, период функции равен 12. Это значит, что все значения повторяются через 12, через . Если мы выберем любую точку на графике функции то через значение функции будет такое же, как и в точке

Аналогично, все значения функции повторяются через . В этих точках значения будут такие же, как и в точке

На каком же расстоянии от точки расположена точка, в которой значение функции такое же, что и в точке ? Очевидно, на расстоянии Это значит, что число делится и на 12, и на 8, то есть является их наименьшим общим кратным. Значит, .

Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых. 

Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции

   

где T — период функции y=f(x). Эта формула позволяет быстро найти период тригонометрических функций такого вида. Для функций y=sin x и y=cos x наименьший положительный период T=2п, для y=tg x и y=ctg x T=п. Рассмотрим на конкретных примерах, как найти период функции, используя данную формулу.

Найти период функции:

1) y=5sin(3x-п/8).

Здесь А=5, k=3, b=-п/8. Для нахождения периода нам нужно только k — число, стоящее перед иксом. Поскольку период синуса T=2п, то период данной функции

   

   

А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то

   

   

А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции

   

   

А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть

   

Докажем следующие утверждения:

1. Наименьший положительный период функций синус и косинус равен 2π

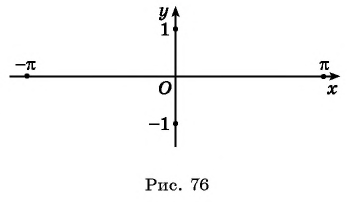
2. Наименьший положительный период функций тангенс и котангенс равен π

Ранее было показано, что число 2π является периодом функций y=cos(x) и y=sin(x). Остается доказать, что число, меньшее 2π, не может являться периодом этих функций.

Если Т – произвольный период косинуса, то cos(a+t)- cos(a) при любом a. Пусть a=0, следовательно cos(T)=cos(0)=1. Наименьшее положительоне число Т, для которого cos(x)=1, есть 2π

Пусть T – произвольный период синуса. Тогда sin(a+T)=sin(a) для любого a. Пусть a=π/2, получаем sin(T+π/2)=sin(π/2)=1. Но sin(x)=1 только при x=π/2+2πn, где n – целое. Следовательно T=2πn. Наименьшее положительное число вида 2πn есть 2π.

Если T – положительный период тангенса, то tg(T)=tg(0+T)=tg(0)=0. Так как на интервале (0;π) тангенс нулей не имеет, следовательно, T ≥ 2π. Ранее было доказано, что π – период функции тангенса, и, значит, π – наименьший положительный период тангенса. Аналогичное доказательство можно привести и для функции котангенса.

Обычно слова “наименьший положительный период” опускают и говорят просто “период”.

Как найти наименьший положительный период функции

Наименьший положительный период функции в тригонометрии обозначается f. Он характеризуется наименьшим значением положительного числа T, то есть меньше его значение T уже не будет являться периодом функции.

Вам понадобится

• – математический справочник.

Инструкция

Обратите внимание на то, что периодическая функция не всегда имеет наименьший положительный период. Так, к примеру, в качестве периода постоянной функции может быть абсолютно любое число, а значит, у нее может и не быть наименьшего положительного периода. Встречаются также и непостоянные периодические функции, у которых нет наименьшего положительного периода. Однако в большинстве случаев наименьший положительный период у периодических функций все же есть.

Наименьший период синуса равен 2?. Рассмотрите доказательство этого на примере функции y=sin(x). Пусть T будет произвольным периодом синуса, в таком случае sin(a+T)=sin(a) при любом значении a. Если a=?/2, получается, что sin(T+?/2)=sin(?/2)=1. Однако sin(x)=1 лишь в том случае, когда x=?/2+2?n, где n представляет собой целое число. Отсюда следует, что T=2?n, а значит, наименьшим положительным значением 2?n является 2?.

Наименьший положительный период косинуса тоже равен 2?. Рассмотрите доказательство этого на примере функции y=cos(x). Если T будет произвольным периодом косинуса, то cos(a+T)=cos(a). В том случае если a=0, cos(T)=cos(0)=1. Ввиду этого, наименьшим положительным значением T, при котором cos(x)=1, есть 2?.

Учитывая тот факт, что 2? – период синуса и косинуса, это же значение будет и периодом котангенса, а также тангенса, однако не минимальным, поскольку, как известно, наименьший положительный период тангенса и котангенса равен ?. Убедиться в этом сможете, рассмотрев следующий пример: точки, соответствующие числам (х) и (х+?) на тригонометрической окружности, имеют диаметрально противоположное расположение. Расстояние от точки (х) до точки (х+2?) соответствует половине окружности. По определению тангенса и котангенса tg(x+?)=tgx, а ctg(x+?)=ctgx, а значит, наименьший положительный период котангенса и тангенса равен ?.

Обратите внимание

Не путайте функции y=cos(x) и y=sin(x) – имея одинаковый период, эти функции изображаются по-разному.

Полезный совет

Для большей наглядности изобразите тригонометрическую функцию, у которой рассчитывается наименьший положительный период.

Источники:

• Справочник по математике, школьная математика, высшая математика

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Содержание:

Рассматривая произвольное действительное число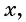

Таким образом, мы установим соответствие между множеством действительных чисел и множеством значений синусов углов. Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию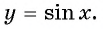 

Определение функция y=sin x

Определение:

Зависимость, при которой каждому действительному числу 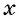 соответствует значение  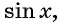называется функцией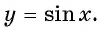 

Рассмотрим свойства функции 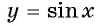 и построим ее график:

Область определения функции y=sin x

Областью определения функции 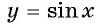 является множество всех действительных чисел, так как для любого  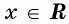существует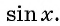 

Графически это означает, что для любой абсциссы найдется точка графика функции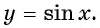 

Множеством значений функции y=sin x

Множеством значений функции 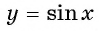 является промежуток  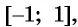так как ординаты точек единичной окружности (значения синусов чисел) изменяются от -1 до 1.

Графически это означает, что график функции 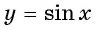 расположен в полосе между прямыми  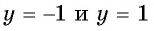(рис. 74).

 

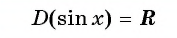
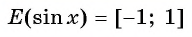
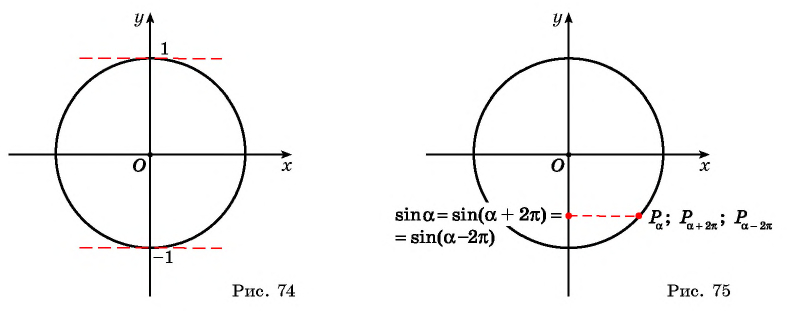
Периодичность функции y=sin x

Периодичность функции 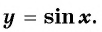Точки единичной окружности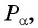 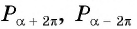 совпадают для любого  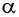(рис. 75), значит, значения синусов этих углов также совпадают, т. е.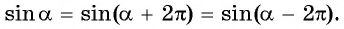 

Говорят, что число 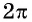 является периодом функции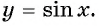 

Определение:

Функция 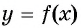 называется периодической функцией с периодом  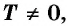если для любого значения  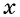из области определения функции числа  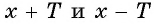также принадлежат области определения и при этом верно равенство

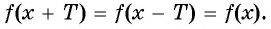
Чтобы определить, является ли функция периодической с периодом 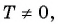 необходимо проверить:

1. принадлежат ли области определения функции числа 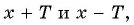 если 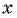 принадлежит области определения функции;
2. выполняется ли равенство 

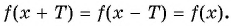
Определим, верно ли, что число 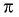 является периодом функции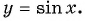 

1. Числа 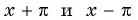 принадлежат области определения функции, так как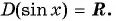 
2. Проверим, выполняется ли равенство 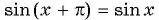 для всех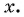 

Пусть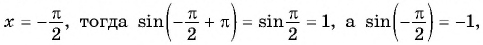 

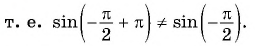
Значит, число 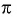 не является периодом функции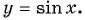 

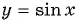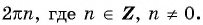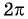Периодом функции  являются числа вида  Число  является наименьшим положительным периодом функции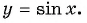 

Функция 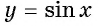 является периодической с наименьшим положительным периодом  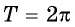(рис. 76). Это означает, что ее график состоит из повторяющихся частей, поэтому достаточно его построить на отрезке длиной  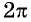(например,  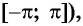а затем повторить построение на каждом следующем отрезке длиной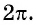 

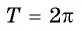
Четность (нечетность) функции y=sin x

Четность (нечетность) функции y=sin x 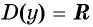 — симметрична относительно нуля. Так как точки  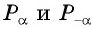единичной окружности симметричны относительно оси абсцисс для любого  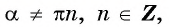то ординаты этих точек противоположны, т. е.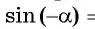 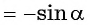 (рис. 77). Значит, функция  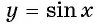нечетная.

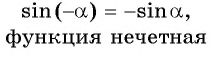
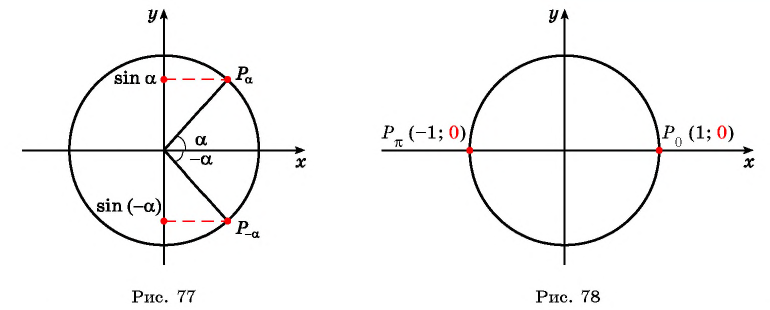
Для построения ее графика достаточно построить его часть для неотрицательных значений аргумента и отобразить эту часть симметрично относительно начала координат.

Нули функции y=sin x

Нули функции. Ординаты точек 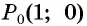 и 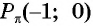 равны нулю. Значит,  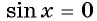в точка  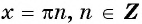(рис. 78), т. е. график функции пересекает ось абсцисс в точках с абсциссами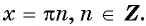 

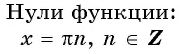
Промежутки знакопостоянства функции y=sin x

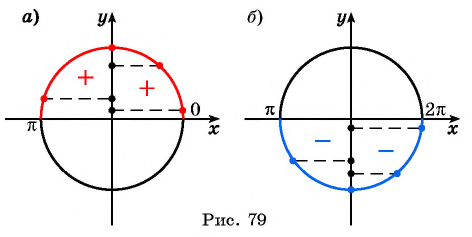
На промежутках 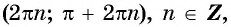 функция  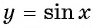принимает положительные значения, так как ординаты точек единичной окружности положительны в первой и во второй четвертях (рис. 79, а).

На промежутках 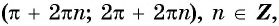функция  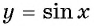принимает отрицательные значения, так как ординаты точек единичной окружности отрицательны в третьей и четвертой четвертях (рис. 79, б).

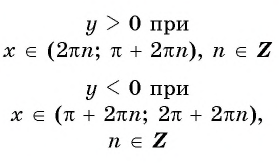
Монотонность функции y=sin x

Монотонность функции. Так как ординаты точек единичной окружности увеличиваются от -1 до 1 при изменении угла от 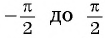 (рис. 80, а) и уменьшаются от 1 до -1 при изменении угла от  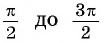(рис. 80, б), то с учетом периодичности определим промежутки возрастания функции  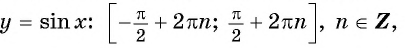и промежутки убывания функции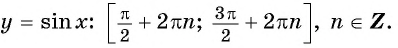 

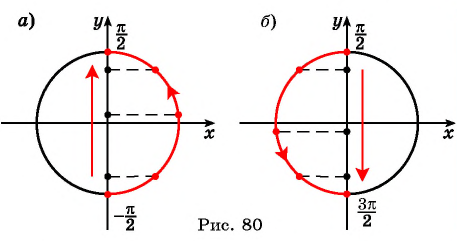
Функции 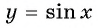 возрастает на промежутках  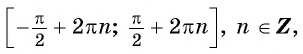и убывает на промежутках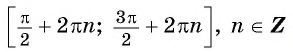 
Наибольшее значение функции 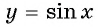 равно 1 и достигается в точках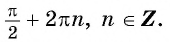 

Наименьшее значение функции 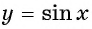 равно 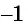 и достигается в точках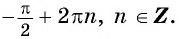 

На основании проведенного исследования построим график функции 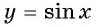 на отрезке от  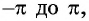длина которого равна  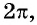т. е. длине периода функции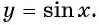 

На этом периоде функция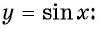 

На рисунке 81 изображена часть графика функции 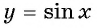 на промежутке от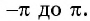 

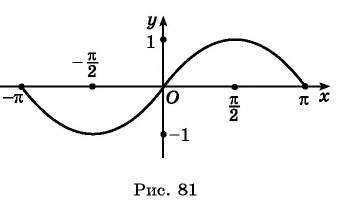
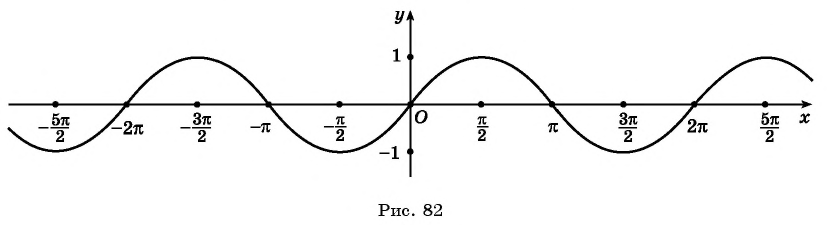
Перенесем эту часть на другие периоды и получим график функции 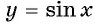(рис. 82). График функции  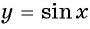называется синусоидой.

Примеры заданий и их решения

Пример №1

Определите, принадлежит ли графику функции 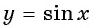 точка: 

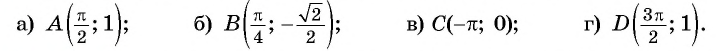
Решение:

а) Подставим в формулу 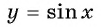 значение аргумента  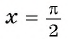найдем соответствующее значение функции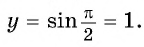 

Полученное значение функции равно ординате точки 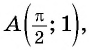 значит, точка  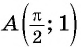принадлежит графику функции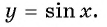 

б)    При 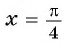 получим  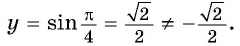Точка 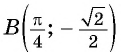 не принадлежит графику функции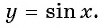 

в)    При 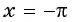 получим  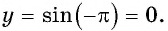Точка 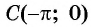 принадлежит графику функции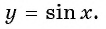 

г)    При 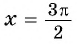 получим  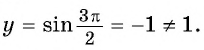Точка 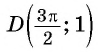 не принадлежит графику функции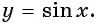 

Пример №2

Найдите область определения и множество значений функции:

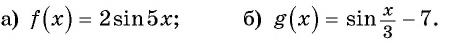
Решение:

а) Так как область определения функции 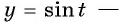 все действительные числа, т.е 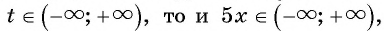значит,  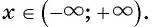  Таким образом,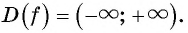 

Множеством значений функции 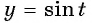 является отрезок  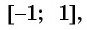значит,  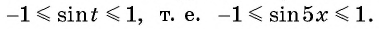Тогда по свойству неравенств  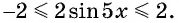Таким образом,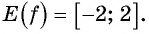 

б) 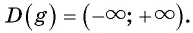 Поскольку  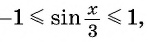то по свойству неравенств

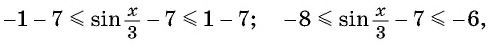 т.е.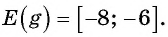 

Пример №3

Найдите наибольшее значение функции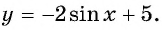 

Решение:

Так как 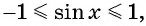 значит,  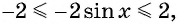тогда 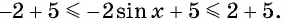 Таким образом, имеем:  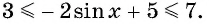Наибольшее значение функции  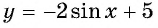равно 7.

• Заказать решение задач по высшей математике

Пример №4

Найдите значение выражения, используя свойство периодичности функции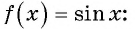 

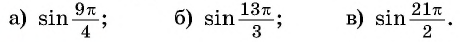
Решение:

Так как число 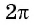 является наименьшим положительным периодом функции  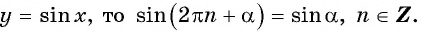Тогда:

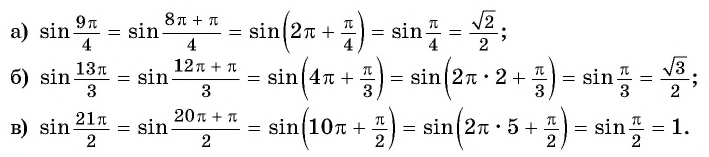
Пример №5

Найдите значение выражения, используя свойство нечетности функции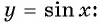 

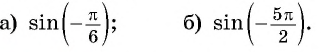
Решение:

Так как функция 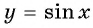 нечетная, то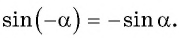

 Тогда:

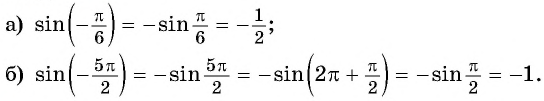
Пример №6

Исследуйте функцию на четность (нечетность):

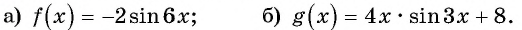
Решение:

a)  — область определения симметрична относительно нуля;

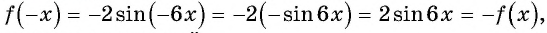 значит, функция является нечетной.

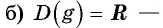 область определения симметрична относительно нуля; 

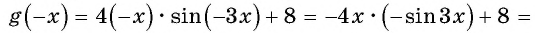
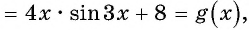значит, функция является четной.

Пример №7

Найдите нули функции:

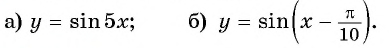
Решение:

а) Пусть 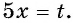 Нулями функции  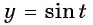являются числ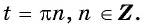а Тогда 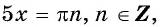 значит,  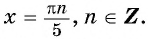Таким тобразом, числа  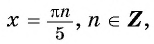являются нулями функции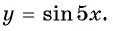 

б) Пусть 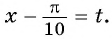   Нулями функции  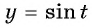являются числ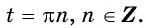а  Тогда 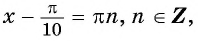 значит,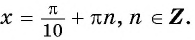 

Таким образом, числа 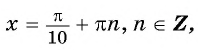 являются нулями функции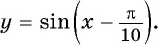 

Пример №8

Определите знак произведения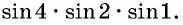 

Решение:

Так как 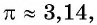 то 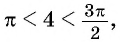 т. е. угол 4 радиана принадлежит промежутку  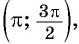на котором функция  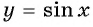принимает отрицательные значения, значит,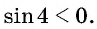 

Углы 2 радиана и 1 радиан принадлежат промежутку 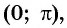 на котором функция  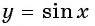принимает положительные значения, т. е.  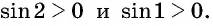Значит,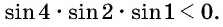 

Пример №9

Что больше: 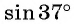 или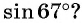 

Решение. Так как функция 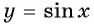 возрастает на промежутке 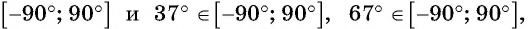то из того, что 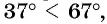следует, что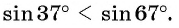 

Пример №10

Постройте график функции:

Решение:

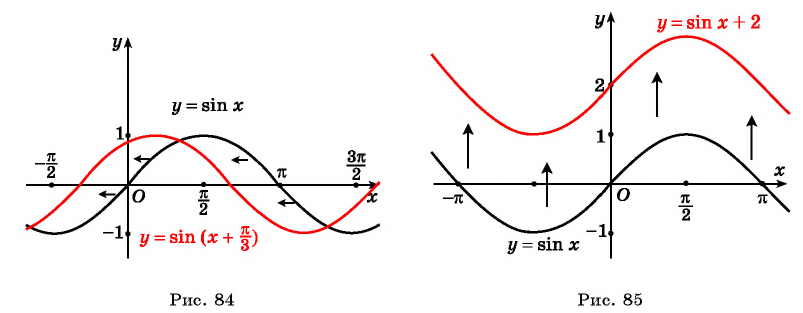
а) График функции 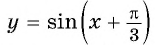 получаем из графика функции  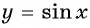сдвигом его вдоль оси абсцисс на  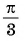влево (рис. 84).

б)    График функции 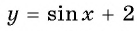 получаем из графика функции  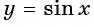сдвигом его вдоль оси ординат на 2 единицы вверх (рис. 85).