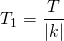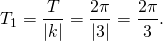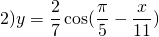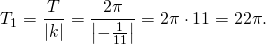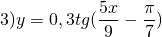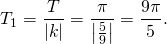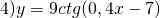Как найти наименьший положительный период по графику - Сайт, где вы сможете решить свои вопросы

Как найти наименьший положительный период функции

Наименьший положительный период функции в тригонометрии обозначается f. Он характеризуется наименьшим значением положительного числа T, то есть меньше его значение T уже не будет являться периодом функции.

Вам понадобится

– математический справочник.

Инструкция

Обратите внимание на то, что периодическая функция не всегда имеет наименьший положительный период. Так, к примеру, в качестве периода постоянной функции может быть абсолютно любое число, а значит, у нее может и не быть наименьшего положительного периода. Встречаются также и непостоянные периодические функции, у которых нет наименьшего положительного периода. Однако в большинстве случаев наименьший положительный период у периодических функций все же есть.

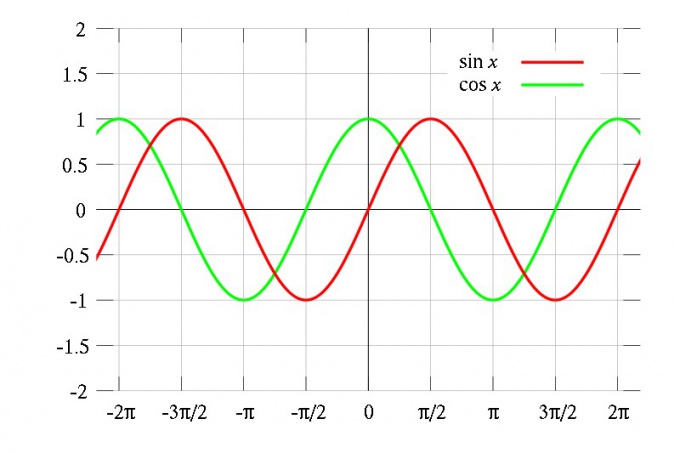
Наименьший период синуса равен 2?. Рассмотрите доказательство этого на примере функции y=sin(x). Пусть T будет произвольным периодом синуса, в таком случае sin(a+T)=sin(a) при любом значении a. Если a=?/2, получается, что sin(T+?/2)=sin(?/2)=1. Однако sin(x)=1 лишь в том случае, когда x=?/2+2?n, где n представляет собой целое число. Отсюда следует, что T=2?n, а значит, наименьшим положительным значением 2?n является 2?.

Наименьший положительный период косинуса тоже равен 2?. Рассмотрите доказательство этого на примере функции y=cos(x). Если T будет произвольным периодом косинуса, то cos(a+T)=cos(a). В том случае если a=0, cos(T)=cos(0)=1. Ввиду этого, наименьшим положительным значением T, при котором cos(x)=1, есть 2?.

Учитывая тот факт, что 2? – период синуса и косинуса, это же значение будет и периодом котангенса, а также тангенса, однако не минимальным, поскольку, как известно, наименьший положительный период тангенса и котангенса равен ?. Убедиться в этом сможете, рассмотрев следующий пример: точки, соответствующие числам (х) и (х+?) на тригонометрической окружности, имеют диаметрально противоположное расположение. Расстояние от точки (х) до точки (х+2?) соответствует половине окружности. По определению тангенса и котангенса tg(x+?)=tgx, а ctg(x+?)=ctgx, а значит, наименьший положительный период котангенса и тангенса равен ?.

Обратите внимание

Не путайте функции y=cos(x) и y=sin(x) – имея одинаковый период, эти функции изображаются по-разному.

Полезный совет

Для большей наглядности изобразите тригонометрическую функцию, у которой рассчитывается наименьший положительный период.

Источники:

Справочник по математике, школьная математика, высшая математика

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Периодические функции

С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.

%D0%B59

Дадим определение периодической функции:

Например, — периодические функции.

Для функций и период

Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:

1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения

График функции может выглядеть, например, вот так:

219

Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.

2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).

Построим график функции при

Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.

Период функции равен 2. Повторим периодически участок длины 2, который уже построен.

220

3. Найдите наименьший положительный период функции

Наименьший положительный период функции равен

График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).

Рассуждая аналогично, получим, что для функции наименьший положительный период равен На отрезке укладывается ровно 5 полных волн функции

4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции

Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.

Источник

Уроки математики и физики для школьников и родителей

суббота, 4 сентября 2021 г.

Урок 5. Периодичность тригонометрических функций

Из этого определения сразу следует, что если Т – период функции

– также периоды функций. Значит у периодической функции бесконечно много периодов.

Чаще всего (но не всегда) среди множества положительных периодов функции можно найти наименьший. Его называют основным периодом .

График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

у = х – [х] , где [х] – целая часть числа. Если к произвольному значение аргумента этой функции добавить 1 , то значение функции от этого не изменится :

Следовательно, при любом значении х

sin (α + 360 ° ) = sin α

Таким образом, функции sin α и cos α от прибавления к аргументу α одного полного оборота ( 2π или 360 ° ) не меняют своих значений.

где k – любое целое число.

Следовательно, функции sin α и cos α – периодические.

Наименьшее положительное число, от прибавления которого к любому допустимому значению аргумента не изменяется значение функции, называется периодом функции.

В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным радиусом ОМ единичной окружности.

отсюда следует, что значения tg α и с tg α не изменяются, если к углу α прибавить любое число полуоборотов:

где k – любое целое число.

вычисляются по формуле

равен наименьшему числу, при делении которого на T ₁ и T ₂ получаются целые числа.

Найти период функции

не существует, так как такого числа, при делении которого на 2π и на 2 получались бы целые числа, нет.

Периода не существует.

Доказать следующее утверждение :

Так как тангенс – периодическая функция с минимальным периодом 20 ∙ 180 ° , то получим :

Доказать следующее утверждение :

Так как косинус – чётная и периодическая функция с минимальным периодом 2π , то получим :

сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.

Доказать следующее утверждение :

Так как синус – нечётная и периодическая функция с минимальным периодом 20 ∙ 360 ° , то получим :

Найти основной период функции

Пусть Т основной период функции, тогда:

так как 2 πk период синуса, то получим :

sin (7х + 7 t ) = sin (7х + 2 πk ),

Найти основной период функции

Пусть Т основной период функции, тогда:

со s 0,3х = со s 0,3(х + t ) = со s (0,3х + 0,3 t )

так как 2 πk период косинуса, то получим :

Найти период функции :

y = 5 sin 2 x + 2 ctg 3х.

Наименьшее число, при делении которого на

Найти период функции :

Находим периоды слагаемых. Период функции

Очевидно, что период заданной функции равен

Найти период функции :

Периода у заданной функции не существует, так как нет такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.

Найти период функции :

Приведём к общему знаменателю периоды :

Тогда наименьшее общее кратное (НОК) будет :

Теперь найдём период заданной функции :

Источник

Как определить периодичность функции

Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.

Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.

Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.

Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.

Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.

Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.

Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.

Источник

Узнать ещё

Знание — сила. Познавательная информация

Как найти период функции

Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции

где T — период функции y=f(x). Эта формула позволяет быстро найти период тригонометрических функций такого вида. Для функций y=sin x и y=cos x наименьший положительный период T=2п, для y=tg x и y=ctg x T=п. Рассмотрим на конкретных примерах, как найти период функции, используя данную формулу.

Найти период функции:

Здесь А=5, k=3, b=-п/8. Для нахождения периода нам нужно только k — число, стоящее перед иксом. Поскольку период синуса T=2п, то период данной функции

А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то

А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции

А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть

Источник

Периодическая функция

Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T (отличного от нуля).

Функция y=f(x) называется периодической, если существует такое число T≠0, что для любого x из области определения этой функции выполняются равенства:

Число T называют периодом функции y=f(x).

Из определения следует, что значения x-T и x+T также входят в область определения функции y=f(x).

Свойства периодических функций

1) По определению периодической функции для любого x из области определения y=f(x) если T — период функции, то f(x-T)= f(x)=f(x+T).

2) Для любого x из области определения y=f(x) если T₁ — период функции, то

Так как T₂ также является периодом функции y=f(x), то для аргумента x-T₁

Следовательно, число T₁+T₂ является периодом функции y=f(x).

3) Это свойство непосредственно вытекает из свойства 2, если T взять в качестве слагаемого n раз.

4) Если T — период функции f(x), то для аргумента kx+b

Значит число T/k — период функции f(kx+b).

5) Эти свойства следуют непосредственно из определения.

Например, для суммы f(x) и g(x):

Из свойства 3 следует, что каждая периодическая функция имеет бесконечно много периодов.

Если среди всех периодов функции y=f(x) существует наименьший положительный период, то его называют главным (или основным) периодом функции.

Примеры периодических функций

1) Поскольку для любого x выполняются равенства

то функции y=sin x и y=cos x являются периодическими с периодом T=2π.

2) Так как для любого x из области определения функции y=tg x выполняется равенство

tg (x-π)=tg x =tg (x-π), то y=tg x — периодическая функция с периодом T=π.

Аналогично, y=ctg x — периодическая функция с периодом T=π.

3) Так как для любого действительного числа x и любого рационального числа k выполняется равенство D(x+k)=D(x), то функция Дирихле D(x) — периодическая с периодом T=k, где k∈Q, k≠0.

Поскольку k — любое рациональное число, невозможно его указать наименьшее положительное значение. Следовательно, функция Дирихле не имеет главного периода.

4) Рассмотрим частный случай линейной функции y=b, b — действительное число (b∈R). Эта функция определена на множестве действительных чисел и при любых значениях аргумента принимает единственное значение y=b, то есть для любого действительного числа m (m∈R), y(x)=y(x+m)=b.

Значит y=b — периодическая функция с периодом T=m, где m∈R, m≠0.

Так как m — любое действительное число, оно не имеет наименьшего положительного значения. Поэтому функция y=b не имеет главного периода.

5) Так как для любого действительного x и любого целого k выполняется равенство =, то функция дробной части числа y= — периодическая с периодом T=k, где k∈Ζ, k≠0.

Наименьшим положительным целым числом является единица. Следовательно, T=1 — главный период функции y=.

Главный период функций y=sin x и y=cos x T=2π.

Главный период функций y=tg x и y=ctg x T=π.

Если T — период функции y=sin x, то sin (x-2π)=sin x = sin (x-2π) для любого x.

То есть любой период функции y=sin x имеет вид 2πn, n∈Z.

Наименьшее положительное значение это выражение принимает при n=1 и оно равно T=2π.

Таким образом, 2π — главный период функции y=sin x.

Аналогично доказываются утверждения о главном периоде функций y=cos x, y=tg x и y=ctg x.

Из 4-го свойства периодических функций непосредственно следует, что для функций y=sin (kx+b) и y=cos (kx+b) (k≠0) наименьший положительный период

а для функций y=tg (kx+b) и y=ctg (kx+b) (k≠0) наименьший положительный период

График периодической функции повторяется через промежутки длиной T (на оси Ox).

Дана часть графика

промежутке длиной T.

Чтобы построить график функции, выполняем параллельный перенос этой части графика вдоль оси Ox на ±T, ±2T,… :

Источник

В этой статье обсуждаем периодичность функций: как определить, периодична ли функция, и каков ее период.

Функция периодична, если некоторый набор ее значений повторяется раз за разом, и точки с одинаковыми значениями функции расположены на числовой оси с равными промежутками. Это расстояние и будем называть периодом. Периодичная функция может иметь и несколько периодов, самый маленький положительный из них будем называть основным.

Тогда, если мы знаем период, мы можем, зная все значения функции на протяжении данного периода, достроить функцию, либо узнать ее значения в любой точке числовой оси – то есть при любом аргументе.

period1

Периодичная функция

Пример 1: функция f(x) имеет период, равный 2: T=2 и при . Найдите значение выражения .

Раз наша функция принимает форму части параболы на отрезке [-2; 0] при периоде, равном 2, значит, такую же форму она будет иметь и на следующем отрезке – [0;2], и на отрезке [2;4]. Изобразим ее:

period2

Определение значения периодичной функции

Видно, что функция принимает одинаковые значения в точках, отстоящих друг от друга на 2, 4, 6 единиц и т.д., тогда . Найдем эти значения функции. В точке (-1) функция принимает значение , в точке (3,5) функция принимает значение .

Теперь найдем значение искомого выражения: .

Строго говоря, функция периодична, если есть такое число Т, что .

Попробуем научиться определять, периодична ли функция или нет. Для этого рассмотрим несколько примеров.

Пример 2. Проверим, периодична ли функция .

Установим, выполняется ли условие: , то есть ? Очевидно, что данное условие не выполняется. Значит, функция непериодична.

Пример 3. Проверим, периодична ли функция .

Функцию для удобства представим в виде: .

Установим, выполняется ли условие: , то есть ? Очевидно, что данное условие не выполняется: . Значит, функция непериодична.

Пример 4. Проверим, периодична ли функция . Если функция периодична, то будет выполняться условие: , то есть . Поскольку нам все равно, в какой точке числовой оси мы проведем свое исследование, то очень удобно начать с точки x=0 . Тогда , или . Это означает, что либо cos T=1 , либо , то есть либо T=2{pi} , либо T={pi} , а так как главным считается наименьший положительный период, то T={pi} .

period3

Определение периода функции

В данном примере делать проверку необязательно, но проверка бывает очень полезна в более сложных задачах, поэтому сделаем ее здесь для тренировки: .

Пример 5. Определить периодичность функции .

Если Т – период, то .

В это равенство подставим какие-нибудь «удобные» точки, например, . Получим:

Далее есть два пути отыскания периода, первый – решение этого уравнения, второй – составление еще одного уравнения такого же вида. Если функция имеет период Т, то верно и следующее: . Подставим «удобную» точку :

Пользуясь четностью косинуса и нечетностью синуса можем записать:

Имеем систему:

Уравнения сложим, и получим

, откуда

, при n=1 получим T={pi} – ведь нам нужен наименьший период.

Теперь испробуем второй путь, решим это уравнение: . Из основного тригонометрического тождества:

${sqrt{1-{sin {2T}}^2}}+2{sin {2T}}=1$

Оставим в левой части только корень:

$sqrt{1-{sin {2T}}^2}=1-2{sin {2T}}$

Возведем в квадрат:

$1-(sin {2T})^2=1-4sin 2T+4(sin {2T})^2$

$5(sin {2T})^2-4sin {2T}=0$

Тогда либо , либо и .

Это уравнение имеет два решения, одно из которых (второе) – посторонний корень, появившийся при возведении в квадрат. Проверка подстановкой его в исходное уравнение позволит нам выявить его и отбросить. Таким образом, получаем:

и наименьшим будет период при n=1 , то есть T={pi} .

Здесь также необходимо сделать проверку. Подставим полученный период в условие :

, то есть

период данной функции – T={pi} .

period1

Определение периода функции

Пример 6. Определить периодичность функции и найти ее основной период.

Если Т – период, то

Подставим x=0 , имеем

Или , , наименьший период при n=1 , T= {pi} .

Проверим:

period4

Определение периода функции

Пример 7. Определим период функции .

Запишем условие периодичности:

, если x=0 , то

, откуда , . При n=1 , , при n=2 , . Проверкой можно показать, что периодом не является. Тогда . Действительно:

Определение периода функции

Пример 8. Доказать, что периодом функции является T=2{pi} .

Тогда:

Пример 9. Доказать, что периодом функции является T=2{pi} .

Тогда:

Если x=0 , то

, а так как {-pi}/4 и {7pi}/4 – одна и та же точка на единичной окружности, то равенство выполняется.

Удачи вам в учебе и надеюсь, эта статья вам помогла.

Источник

ВИДЕО УРОК

Периодические функции.

Функцию у = f(х), х ∈ Х, называют периодической,
если существует такое отличное от нуля число
Т, что для любого х из области определения функции справедливо
равенство:

f(х + Т) = f(х) = f(х – Т).

Число Т называют периодом функции у = f(х).

Из этого
определения сразу следует, что если Т –
период функции

у = f(х), то

2Т, 3Т, 4Т, –Т, –2Т, –3Т,
–4Т

– также периоды
функций. Значит у периодической функции бесконечно много периодов.

Если Т – период функции, то число вида kТ,
где k – любое целое
число, также является периодом функции.

Чаще всего (но не
всегда) среди множества положительных периодов функции можно найти наименьший.
Его называют основным периодом.

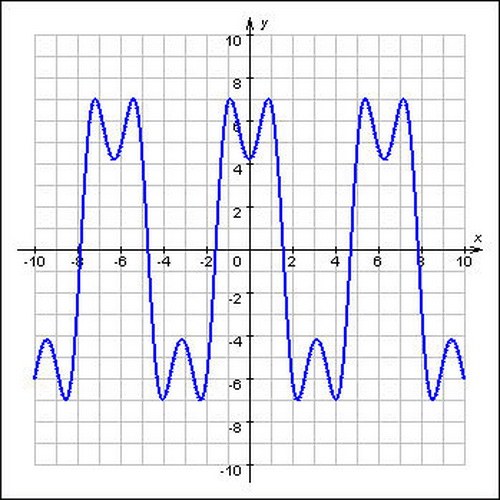
График периодической
функции состоит из неограниченно повторяющихся одинаковых фрагментов.

График каждой
периодической функции состоит из одинаковых линий повторяющихся и изолированных
друг от друга, как в рассматриваемом случае, или соединенных в одну общую линию
(синусоида и другие.)

Графики
периодических функций обладают следующей особенностью. Если Т – основной период функции у = f(х), то для построения её графика достаточно построить ветвь
графика на одном из промежутков оси х длиной
Т, а затем осуществить параллельный перенос этой ветви по
оси х на

± Т, ±
2Т, ± 3Т, …

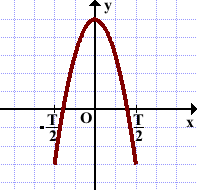
Чаще всего в
качестве такого промежутка длиной Т выбирают промежуток с концами в точках

(–^Т/₂; 0) и (^Т/₂; 0) или

(0; 0) и (Т; 0).

ПРИМЕР:

Рассмотрим функцию

у = х – [х], где [х] – целая часть числа. Если к
произвольному значение аргумента этой функции добавить 1, то значение функции от этого не изменится:

f(x + 1) = (x
+1) – [x + 1] = x + 1 – [x] – 1
= x – [x] = f (x).

Следовательно, при любом
значении х

f(x + 1) = f(x).

А это значит, что рассматриваемая функция
периодическая, период которой равен 1. Любое целое число
также является периодом данной функции, но обычно рассматривают только
маленький положительный период функции.

График этой функции
приведен на рисунке. Он состоит из бесконечного множества равных отрезков, которые
повторяются.

Периодичность тригонометрических функций.

Возьмём произвольный угол α и построим
подвижной радиус ОМ единичной окружности такой, что угол,
составленный с осью Ох этим радиусом, равен α.

Если мы к углу прибавим
2π или 360° (то есть полный
оборот), то углу α + 2π или α + 360° будет соответствовать то же положение
подвижного радиуса ОМ, что для угла α.

Так как синус и косинус угла,
составленного с осью Ох подвижным радиусом ОМ единичной
окружности, по сути соответственно ордината
у и
абсцисса х точки М, то

sin (α + 2π) = sin α или

sin (α + 360°) = sin α

cos (α + 2π)
= cos α или

cos (α + 360°) = cos α.

Таким образом, функции sin α и cos α от
прибавления к аргументу α одного
полного оборота (2π или 360°) не меняют своих значений.

Точно так же, прибавляя к
углу α любое целое
число полных оборотов, мы не изменим положения подвижного радиуса ОМ, а потому:

sin (α + 2kπ) = sin α или

sin (α + 360°k) = sin α

cos (α + 2kπ) = cos α или

cos (α + 360°k) = cos α,

где k – любое целое
число.

Функции, обладающие таким
свойством, что их значения не изменяются от прибавления к любому допустимому
значению аргумента определённого постоянного числа, называются периодическими.

Следовательно, функции sin α и cos α – периодические.

Наименьшее положительное число,
от прибавления которого к любому допустимому значению аргумента не изменяется
значение функции, называется периодом функции.

Периодом функции sin α и cos α
является 2π или 360°.

Функции tg α и сtg α также
периодические и их периодом является число
π или 180°.

В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным
радиусом ОМ единичной окружности.

Построим точку М‘,

симметричную точке М относительно
начала координат. Один из углов, образованных с осью Ох подвижным
радиусом ОМ‘, будет равен α + π.

Если х и у – координаты точки
М, то точки М‘ будут –х и –у. Поэтому

sin α = у, cos α = х,

sin (α + π) = –у,

cos (α + π) = –х.

Отсюда

и, следовательно,

tg (α + π) = tg α,

сtg (α + π)
= сtg α.

отсюда следует, что значения tg α и сtg α не
изменяются, если к углу α прибавить любое число полуоборотов:

tg (α + kπ) = tg α,

сtg (α + kπ) = сtg α.

где k – любое целое
число.

Периоды функций

y = A sin (ωx + φ) и

y = A cos (ωx + φ)

вычисляются по формуле

T = ^2π/_ω,

а период функции

y = A tg (ωx + φ)

по формуле

T = ^π/_ω.

Если период функции y = f(x) равен T₁, а период функции y = g(x) равен T₂, то период функций

y = f(x) + g(x) и

y = f(x) – g(x)

равен наименьшему числу, при делении которого
на T₁ и T₂ получаются целые числа.

ПРИМЕР:

Найти
период функции

y = 3 sin (x – 2) + 7 соs πx.

РЕШЕНИЕ:

Период
функции

y = 3 sin (x – 2)

равен

T₁= ^2π/₁ = 2π.

Период
функции

y = 7 соs πx

равен

T₂= ^2π/_π = 2.

Периода
у функции

y = 3 sin (x – 2) + 7 соs πx

не
существует, так как такого числа, при делении которого на 2π и
на 2 получались бы целые числа, нет.

ОТВЕТ:

Периода
не существует.

ПРИМЕР:

Доказать
следующее утверждение:

tg
3850° = tg 250°.

РЕШЕНИЕ:

Так как тангенс – периодическая функция с минимальным
периодом 20 ∙ 180°, то получим:

tg
3850° = tg (20 ∙ 180° + 250°) = tg 250°.

ПРИМЕР:

Доказать
следующее утверждение:

сos (–13π) = –1.

РЕШЕНИЕ:

Так как косинус – чётная и периодическая функция с
минимальным периодом 2π, то получим:

сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.

ПРИМЕР:

Доказать
следующее утверждение:

sin (–7210°) = – sin 10°.

РЕШЕНИЕ:

Так как синус – нечётная и периодическая функция с
минимальным периодом 20 ∙ 360°, то получим:

sin (–7210°) = –sin 7210° = –sin (20 ∙ 360° + 10°) – sin 10°.

ПРИМЕР:

Найти основной период функции

sin 7х.

РЕШЕНИЕ:

Пусть Т основной период функции, тогда:

sin 7х = sin 7(х + t) = sin (7х + 7t)

так как 2πk период синуса, то получим:

sin (7х + 7t) = sin (7х + 2πk),

ОТВЕТ:

ПРИМЕР:

Найти основной период функции

соs 0,3х.

РЕШЕНИЕ:

Пусть Т основной период функции, тогда:

соs 0,3х = соs 0,3(х + t)
= соs (0,3х + 0,3t)

так как 2πk период косинуса, то получим:

соs (0,3х + 0,3t) = соs (0,3х + 2πk),

ОТВЕТ:

ПРИМЕР:

Найти период функции:

y = 5sin 2x + 2ctg 3х.

РЕШЕНИЕ:

Период функции

y = 5sin 2x

равен Т₁ = ²^𝜋/₂ = π,

а период функции

y = 2ctg 3х

равен Т₂ = ^𝜋/₃.

Наименьшее число, при делении которого на

Т₁ = π и Т₂ = ^𝜋/₃

– получаются целые числа будет число π.
Следовательно, период заданной функции равен Т = π.

ПРИМЕР:

Найти период функции:

y = 9sin (5x + ^π/₃) – 4cоs (7х + 2).

РЕШЕНИЕ:

Находим периоды слагаемых. Период функции

y = 9sin (5x + ^π/₃)

равен Т₁ = ²^𝜋/₅,

а период функции

y = 4cоs (7х + 2)

равен Т₂ = ²^𝜋/₇.

Очевидно, что период заданной функции равен

Т = 2π.

ПРИМЕР:

Найти период функции:

y = 3sin πx + 8tg (х + 5).

РЕШЕНИЕ:

Период функции

y = 3sin πx

равен Т₁ = ²^π/_π = 2,

а период функции

y = 8tg (х + 5)

равен Т₂ = ^𝜋/₁ = π.

Периода у заданной функции не существует, так как нет
такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.

ПРИМЕР:

Найти период функции:

y = sin 3x + соs 5х.

РЕШЕНИЕ:

Период функции

y = sin 3x

равен Т₁ = ²^π/₃,

а период функции

y = соs 5х

равен Т₂ = ²^π/₅.

Приведём к общему знаменателю периоды:

Т₁ = ¹⁰^π/₁₅, Т₂ = ⁶^π/₁₅.

Тогда наименьшее общее кратное (НОК) будет:

НОК (10π; 6π)
= 30π.

Теперь найдём период заданной функции:

Т = ^30π/₁₅ = 2π.

Задания к уроку 5

Задание 1

Задание 2

Задание 3

ДРУГИЕ УРОКИ

Урок 1. Градусное измерение угловых величин

Урок 2. Радианное измерение угловых величин

Урок 3. Основные тригонометрические функции

Урок 4. Натуральные тригонометрические таблицы

Урок 6. Область определения и область значения тригонометрических функций

Урок 7. Знаки тригонометрических функций

Урок 8. Чётность и нечётность тригонометрических функций

Урок 9. Тригонометрические функции некоторых углов

Урок 10. Построение угла по данному значению его тригонометрической функции

Урок 11. Основные тригонометрические тождества

Урок 12. Выражение всех тригонометрических функций через одну из них

Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций

Урок 14. Теорема синусов

Урок 15. Теорема косинусов

Урок 16. Решение косоугольных треугольников

Урок 17. Примеры решения задач по планиметрии с применением тригонометрии

Урок 18. Решение практических задач с помощью тригонометрии

Урок 19. Формулы приведения (1)

Урок 20. Формулы приведения (2)

Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций

Урок 22. Формулы двойных и тройных углов (аргументов)

Урок 23. Формулы половинного аргумента

Урок 24. Формулы преобразования суммы тригонометрических функций в произведение

Урок 25. Графики функций y = sin x и y = cos x

Урок 26. Графики функций y = tg x и y = ctg x

Урок 27. Обратные тригонометрические функции

Урок 28. Основные тождества обратных тригонометрических функций

Урок 29. Выражение одной из аркфункций через другие

Урок 30. Графики обратных тригонометрических функций

Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований

Источник

Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции

$[{T_1} = frac{T}{{left| k right|}}]$

Найти период функции:

1) y=5sin(3x-п/8).

$[{T_1} = frac{T}{{left| k right|}} = frac{{2pi }}{{left| 3 right|}} = frac{{2pi }}{3}.]$

$[2)y = frac{2}{7}cos (frac{pi }{5} - frac{x}{{11}})]$

А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то

$[{T_1} = frac{T}{{left| k right|}} = frac{{2pi }}{{left| { - frac{1}{{11}}} right|}} = 2pi cdot 11 = 22pi .]$

$[3)y = 0,3tg(frac{{5x}}{9} - frac{pi }{7})]$

А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции

$[{T_1} = frac{T}{{left| k right|}} = frac{pi }{{left| {frac{5}{9}} right|}} = frac{{9pi }}{5}.]$

А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть

$[{T_1} = frac{T}{{left| k right|}} = frac{pi }{{left| {0,4} right|}} = frac{{10pi }}{4} = frac{{5pi }}{2}.]$

Источник

Как найти наименьший положительный период функции

Периодические функции

Уроки математики и физики для школьников и родителей

суббота, 4 сентября 2021 г.

Урок 5. Периодичность тригонометрических функций

Как определить периодичность функции

Узнать ещё

Как найти период функции

Периодическая функция

Задание 1 Задание 2 Задание 3

Вам также может понравиться

Как исправить ауру человека

Майнкрафт как найти храм в воде

Как найти задолженность налога на имущество

Добавить комментарий Отменить ответ

Задание 1

Задание 2

Задание 3