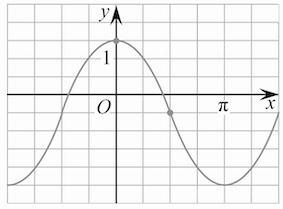
Как найти наименьший положительный период тригонометрической функции

С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.

Дадим определение периодической функции:

Функция y=f(x) называется периодической, если существует такое число , не равное нулю, что для любого из ее области определения

Другими словами, это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого фиксированного ненулевого числа . Число называется периодом функции. Как правило, говоря о периоде, мы имеем в виду наименьший положительный период функции.

Например, — периодические функции.

Для функций и период T = 2pi ,

Для функций tg x и период T = pi.

Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:

1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения

График функции может выглядеть, например, вот так:

Отметим точку М (1; 5), принадлежащую графику функции . Поскольку период функции равен 2, значения функции в точках будут также равны пяти. Здесь k — целое число.

Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.

Значения функции в точках -3 и 7 равны пяти. Мы получим:

2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).

Построим график функции при

Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.

Период функции равен 2. Повторим периодически участок длины 2, который уже построен.

Найдем f(4)

3. Найдите наименьший положительный период функции

Наименьший положительный период функции равен 2pi.

График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).

Значит, у функции частота в 3 раза больше, чем у функции , а наименьший положительный период в 3 раза меньше и равен $frac{{rm 2}pi }{{rm 3}}$ . Значит, на отрезке 2pi укладывается ровно 3 полных волны функции

Рассуждая аналогично, получим, что для функции наименьший положительный период равен $frac{{rm 2}pi }{{rm 5}}.$ На отрезке 2pi укладывается ровно 5 полных волн функции

Числа 3 и 5 — взаимно простые. Поэтому наименьший положительный период функции равен 2pi .

4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции

По условию, период функции равен 12. Это значит, что все значения повторяются через 12, через . Если мы выберем любую точку x_0 на графике функции то через значение функции будет такое же, как и в точке x_0.

Аналогично, все значения функции повторяются через . В этих точках значения будут такие же, как и в точке x_0.

На каком же расстоянии от точки x_0 расположена точка, в которой значение функции такое же, что и в точке x_0 ? Очевидно, на расстоянии Это значит, что число делится и на 12, и на 8, то есть является их наименьшим общим кратным. Значит, T = 24 .

Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Периодические функции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник

ВИДЕО УРОК

Периодические функции.

Функцию у = f(х), х ∈ Х, называют периодической,
если существует такое отличное от нуля число
Т, что для любого х из области определения функции справедливо
равенство:

f(х + Т) = f(х) = f(х – Т).

Число Т называют периодом функции у = f(х).

Из этого
определения сразу следует, что если Т –
период функции

у = f(х), то

2Т, 3Т, 4Т, –Т, –2Т, –3Т,
–4Т

– также периоды
функций. Значит у периодической функции бесконечно много периодов.

Если Т – период функции, то число вида kТ,
где k – любое целое
число, также является периодом функции.

Чаще всего (но не
всегда) среди множества положительных периодов функции можно найти наименьший.
Его называют основным периодом.

График периодической
функции состоит из неограниченно повторяющихся одинаковых фрагментов.

График каждой
периодической функции состоит из одинаковых линий повторяющихся и изолированных
друг от друга, как в рассматриваемом случае, или соединенных в одну общую линию
(синусоида и другие.)

Графики
периодических функций обладают следующей особенностью. Если Т – основной период функции у = f(х), то для построения её графика достаточно построить ветвь
графика на одном из промежутков оси х длиной
Т, а затем осуществить параллельный перенос этой ветви по
оси х на

± Т, ±
2Т, ± 3Т, …

Чаще всего в
качестве такого промежутка длиной Т выбирают промежуток с концами в точках

(–^Т/₂; 0) и (^Т/₂; 0) или

(0; 0) и (Т; 0).

ПРИМЕР:

Рассмотрим функцию

у = х – [х], где [х] – целая часть числа. Если к
произвольному значение аргумента этой функции добавить 1, то значение функции от этого не изменится:

f(x + 1) = (x
+1) – [x + 1] = x + 1 – [x] – 1
= x – [x] = f (x).

Следовательно, при любом
значении х

f(x + 1) = f(x).

А это значит, что рассматриваемая функция
периодическая, период которой равен 1. Любое целое число
также является периодом данной функции, но обычно рассматривают только
маленький положительный период функции.

График этой функции
приведен на рисунке. Он состоит из бесконечного множества равных отрезков, которые
повторяются.

Периодичность тригонометрических функций.

Возьмём произвольный угол α и построим
подвижной радиус ОМ единичной окружности такой, что угол,
составленный с осью Ох этим радиусом, равен α.

Если мы к углу прибавим
2π или 360° (то есть полный
оборот), то углу α + 2π или α + 360° будет соответствовать то же положение
подвижного радиуса ОМ, что для угла α.

Так как синус и косинус угла,
составленного с осью Ох подвижным радиусом ОМ единичной
окружности, по сути соответственно ордината
у и
абсцисса х точки М, то

sin (α + 2π) = sin α или

sin (α + 360°) = sin α

cos (α + 2π)
= cos α или

cos (α + 360°) = cos α.

Таким образом, функции sin α и cos α от
прибавления к аргументу α одного
полного оборота (2π или 360°) не меняют своих значений.

Точно так же, прибавляя к
углу α любое целое
число полных оборотов, мы не изменим положения подвижного радиуса ОМ, а потому:

sin (α + 2kπ) = sin α или

sin (α + 360°k) = sin α

cos (α + 2kπ) = cos α или

cos (α + 360°k) = cos α,

где k – любое целое
число.

Функции, обладающие таким
свойством, что их значения не изменяются от прибавления к любому допустимому
значению аргумента определённого постоянного числа, называются периодическими.

Следовательно, функции sin α и cos α – периодические.

Наименьшее положительное число,
от прибавления которого к любому допустимому значению аргумента не изменяется
значение функции, называется периодом функции.

Периодом функции sin α и cos α
является 2π или 360°.

Функции tg α и сtg α также
периодические и их периодом является число
π или 180°.

В самом деле, пусть α – произвольный угол, составленный с осью Ох подвижным
радиусом ОМ единичной окружности.

Построим точку М‘,

симметричную точке М относительно
начала координат. Один из углов, образованных с осью Ох подвижным
радиусом ОМ‘, будет равен α + π.

Если х и у – координаты точки
М, то точки М‘ будут –х и –у. Поэтому

sin α = у, cos α = х,

sin (α + π) = –у,

cos (α + π) = –х.

Отсюда

и, следовательно,

tg (α + π) = tg α,

сtg (α + π)
= сtg α.

отсюда следует, что значения tg α и сtg α не
изменяются, если к углу α прибавить любое число полуоборотов:

tg (α + kπ) = tg α,

сtg (α + kπ) = сtg α.

где k – любое целое
число.

Периоды функций

y = A sin (ωx + φ) и

y = A cos (ωx + φ)

вычисляются по формуле

T = ^2π/_ω,

а период функции

y = A tg (ωx + φ)

по формуле

T = ^π/_ω.

Если период функции y = f(x) равен T₁, а период функции y = g(x) равен T₂, то период функций

y = f(x) + g(x) и

y = f(x) – g(x)

равен наименьшему числу, при делении которого
на T₁ и T₂ получаются целые числа.

ПРИМЕР:

Найти
период функции

y = 3 sin (x – 2) + 7 соs πx.

РЕШЕНИЕ:

Период
функции

y = 3 sin (x – 2)

равен

T₁= ^2π/₁ = 2π.

Период
функции

y = 7 соs πx

равен

T₂= ^2π/_π = 2.

Периода
у функции

y = 3 sin (x – 2) + 7 соs πx

не
существует, так как такого числа, при делении которого на 2π и
на 2 получались бы целые числа, нет.

ОТВЕТ:

Периода
не существует.

ПРИМЕР:

Доказать
следующее утверждение:

tg
3850° = tg 250°.

РЕШЕНИЕ:

Так как тангенс – периодическая функция с минимальным
периодом 20 ∙ 180°, то получим:

tg
3850° = tg (20 ∙ 180° + 250°) = tg 250°.

ПРИМЕР:

Доказать
следующее утверждение:

сos (–13π) = –1.

РЕШЕНИЕ:

Так как косинус – чётная и периодическая функция с
минимальным периодом 2π, то получим:

сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.

ПРИМЕР:

Доказать
следующее утверждение:

sin (–7210°) = – sin 10°.

РЕШЕНИЕ:

Так как синус – нечётная и периодическая функция с
минимальным периодом 20 ∙ 360°, то получим:

sin (–7210°) = –sin 7210° = –sin (20 ∙ 360° + 10°) – sin 10°.

ПРИМЕР:

Найти основной период функции

sin 7х.

РЕШЕНИЕ:

Пусть Т основной период функции, тогда:

sin 7х = sin 7(х + t) = sin (7х + 7t)

так как 2πk период синуса, то получим:

sin (7х + 7t) = sin (7х + 2πk),

ОТВЕТ:

ПРИМЕР:

Найти основной период функции

соs 0,3х.

РЕШЕНИЕ:

Пусть Т основной период функции, тогда:

соs 0,3х = соs 0,3(х + t)
= соs (0,3х + 0,3t)

так как 2πk период косинуса, то получим:

соs (0,3х + 0,3t) = соs (0,3х + 2πk),

ОТВЕТ:

ПРИМЕР:

Найти период функции:

y = 5sin 2x + 2ctg 3х.

РЕШЕНИЕ:

Период функции

y = 5sin 2x

равен Т₁ = ²^𝜋/₂ = π,

а период функции

y = 2ctg 3х

равен Т₂ = ^𝜋/₃.

Наименьшее число, при делении которого на

Т₁ = π и Т₂ = ^𝜋/₃

– получаются целые числа будет число π.
Следовательно, период заданной функции равен Т = π.

ПРИМЕР:

Найти период функции:

y = 9sin (5x + ^π/₃) – 4cоs (7х + 2).

РЕШЕНИЕ:

Находим периоды слагаемых. Период функции

y = 9sin (5x + ^π/₃)

равен Т₁ = ²^𝜋/₅,

а период функции

y = 4cоs (7х + 2)

равен Т₂ = ²^𝜋/₇.

Очевидно, что период заданной функции равен

Т = 2π.

ПРИМЕР:

Найти период функции:

y = 3sin πx + 8tg (х + 5).

РЕШЕНИЕ:

Период функции

y = 3sin πx

равен Т₁ = ²^π/_π = 2,

а период функции

y = 8tg (х + 5)

равен Т₂ = ^𝜋/₁ = π.

Периода у заданной функции не существует, так как нет
такого числа, при делении которого на 2 и на π одновременно получались бы целые числа.

ПРИМЕР:

Найти период функции:

y = sin 3x + соs 5х.

РЕШЕНИЕ:

Период функции

y = sin 3x

равен Т₁ = ²^π/₃,

а период функции

y = соs 5х

равен Т₂ = ²^π/₅.

Приведём к общему знаменателю периоды:

Т₁ = ¹⁰^π/₁₅, Т₂ = ⁶^π/₁₅.

Тогда наименьшее общее кратное (НОК) будет:

НОК (10π; 6π)
= 30π.

Теперь найдём период заданной функции:

Т = ^30π/₁₅ = 2π.

Задания к уроку 5

Задание 1

Задание 2

Задание 3

ДРУГИЕ УРОКИ

Урок 1. Градусное измерение угловых величин

Урок 2. Радианное измерение угловых величин

Урок 3. Основные тригонометрические функции

Урок 4. Натуральные тригонометрические таблицы

Урок 6. Область определения и область значения тригонометрических функций

Урок 7. Знаки тригонометрических функций

Урок 8. Чётность и нечётность тригонометрических функций

Урок 9. Тригонометрические функции некоторых углов

Урок 10. Построение угла по данному значению его тригонометрической функции

Урок 11. Основные тригонометрические тождества

Урок 12. Выражение всех тригонометрических функций через одну из них

Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций

Урок 14. Теорема синусов

Урок 15. Теорема косинусов

Урок 16. Решение косоугольных треугольников

Урок 17. Примеры решения задач по планиметрии с применением тригонометрии

Урок 18. Решение практических задач с помощью тригонометрии

Урок 19. Формулы приведения (1)

Урок 20. Формулы приведения (2)

Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций

Урок 22. Формулы двойных и тройных углов (аргументов)

Урок 23. Формулы половинного аргумента

Урок 24. Формулы преобразования суммы тригонометрических функций в произведение

Урок 25. Графики функций y = sin x и y = cos x

Урок 26. Графики функций y = tg x и y = ctg x

Урок 27. Обратные тригонометрические функции

Урок 28. Основные тождества обратных тригонометрических функций

Урок 29. Выражение одной из аркфункций через другие

Урок 30. Графики обратных тригонометрических функций

Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований

Источник

Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции

$[{T_1} = frac{T}{{left| k right|}}]$

где T — период функции y=f(x). Эта формула позволяет быстро найти период тригонометрических функций такого вида. Для функций y=sin x и y=cos x наименьший положительный период T=2п, для y=tg x и y=ctg x T=п. Рассмотрим на конкретных примерах, как найти период функции, используя данную формулу.

Найти период функции:

1) y=5sin(3x-п/8).

Здесь А=5, k=3, b=-п/8. Для нахождения периода нам нужно только k — число, стоящее перед иксом. Поскольку период синуса T=2п, то период данной функции

$[{T_1} = frac{T}{{left| k right|}} = frac{{2pi }}{{left| 3 right|}} = frac{{2pi }}{3}.]$

$[2)y = frac{2}{7}cos (frac{pi }{5} - frac{x}{{11}})]$

А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то

$[{T_1} = frac{T}{{left| k right|}} = frac{{2pi }}{{left| { - frac{1}{{11}}} right|}} = 2pi cdot 11 = 22pi .]$

$[3)y = 0,3tg(frac{{5x}}{9} - frac{pi }{7})]$

А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции

$[{T_1} = frac{T}{{left| k right|}} = frac{pi }{{left| {frac{5}{9}} right|}} = frac{{9pi }}{5}.]$

А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть

$[{T_1} = frac{T}{{left| k right|}} = frac{pi }{{left| {0,4} right|}} = frac{{10pi }}{4} = frac{{5pi }}{2}.]$

Источник

16
Сен 2022

Категория: 10 Графики функций

2022-09-16
2022-09-16

Задача 1. На рисунке изображён график функции Найдите

Решение: + показать

Задача 2. На рисунке изображён график функции Найдите

Решение: + показать

Задача 3. На рисунке изображён график функции Найдите

Решение: + показать

Задача 4. На рисунке изображён график функции Найдите

Решение: + показать

Задача 5. На рисунке изображён график функции Найдите

Решение: + показать

Задача 6. На рисунке изображён график функции где и – целые. Найдите $f(-frac{8}{3}).$

Решение: + показать

Задача 7. На рисунке изображён график функции $f(x)=acos(frac{pi x}{b}+c)+d,$ где и – целые. Найдите $f(f(-frac{20}{3})).$

Решение: + показать

Пройти тест

Автор: egeMax |

Нет комментариев

Источник

Описание презентации по отдельным слайдам:

1 слайд

Периодичность
тригонометрических
функций
11 класс
2 слайд

Определение:
Функция f(x) называется периодической, если существует такое число Т≠0,что для любого х из области определения этой функции значения х+Т и х-Т также принадлежат области определения и выполняются равенства
f(x-Т)=f(x)=f(x+Т).
Число Т называется периодом функции f(x)
3 слайд

Задача1

Доказать,что f(x)=sinx+1 является периодической с периодом 2π

Решение:
Функция f(x)=sinx+1 определена на R.
f(x+2π)=sin(x+2π)+1=sinx+1=f(x)
4 слайд

Задача 2
Доказать ,что функция f(x)=
является периодической с периодом 2π
Решение:
x
f(x+2π)=
5 слайд

Задача 3
Доказать,что f(x)=
является периодической с периодом 2π
Решение:
x
f (x+2π)=
6 слайд

Задача 4
Доказать ,что функция f(x) =sin2x является периодической с периодом Т=π
Решение:
f (x+π)=sin2(x+π)=sin(2x+2π)=sin2x=f(x)
x
7 слайд

Задача 5
Доказать ,что функция f(x)=tg2x является периодической с периодом Т=
Решение:
8 слайд

Задача 6
Найти наименьший положительный период функции
Решение:
f(x+Т)=f(x)
Наименьший положительный период при n=1
9 слайд

Задача 7
Найти наименьший положительный период функции
Решение:
10 слайд

Наименьший положительный период функции при n=1 Т=2π
11 слайд

Следствие:
Если f(x) имеет период Т,то f(kx) имеет период
Например ,y=sinx Т=2π. y=sin5x,Т=
12 слайд

Задача 8
Найти наименьший положительный период функции
Решение:
Функция y=cosx имеет период 2π.

Функция
имеет период
13 слайд

Задача 9
Найти наименьший положительный период функции
Решение:
Так как функция sin2x имеет период
а функция cos3x имеет период
то период Т функции
будет такое наименьшее положительное число, которое кратно
одновременно,т.е.наименьшее общее кратное.Т=2π
14 слайд

Задача 10
Найти наименьший положительный период функции
Решение:
Так как функция
имеет период
а функция
имеет период
то период Т функции
будет такое наименьшее положительное число, которое кратно
одновременно,т.е наименьшее общее кратное. Т=6π