Свойства углов между диагоналями параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
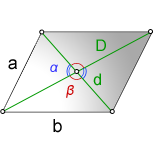
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол между диагоналями
β – тупой угол между диагоналями
Формулы косинуса острого и тупого углов между диагоналями, через стороны и диагонали (по теореме косинусов):
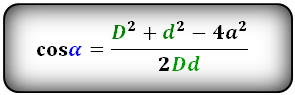
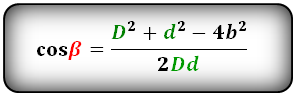
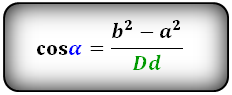
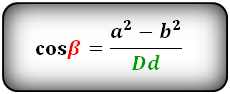
Формула синуса острого и тупого углов через площадь (S) и диагонали:
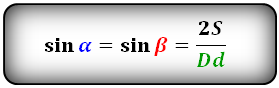
Формулы соотношения острого и тупого углов между диагоналями:

Для определения величины угла в градусах или радианах, используем функции arccos и arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 06 ноября 2011
-
Обновлено: 13 августа 2021
Задания
Версия для печати и копирования в MS Word
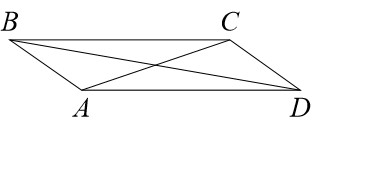
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и
Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.
Спрятать решение
Решение.
Пусть точка пересечения диагоналей — точка O. Диагонали параллелограмма точкой пересечения делятся пополам, откуда AO = OC = AB = CD. Поскольку OC = CD, треугольник COD — равнобедренный, следовательно, ∠COD = ∠CDO = (180° − ∠ACD)/2 = 159°/2 = 79,5°. Угол COD является искомым углом между диагоналями параллелограмма.
Ответ: 79,5.
Задача 6780 В параллелограмме ABCD диагональ AC в 2…
Условие

В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ACD = 139°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
математика 10-11 класс
23616
Решение
Угол СOD=(180-139)/2=20,5
Ответ: 20,5
Написать комментарий
Параллелограмм – это четырехугольник, у которого противолежащие стороны попарно параллельны. Частными
случаями параллелограмма являются прямоугольник и ромб. Квадрат одновременно является частным
случаем и прямоугольника и ромба, поэтому все выявленные для параллелограмма зависимости справедливы
для прямоугольника, квадрата и ромба.
На практике необходимость определения угла между диагоналями на основе прочих элементов может
возникнуть, в частности, при необходимости производства построений на местности и для перепроверки
уже проведенных построений.
- Острый угол между диагоналями параллелограмма через площадь
и диагонали - Угол между диагоналями параллелограмма через диагонали и
сторону - Угол между диагоналями параллелограмма через две стороны и
диагонали
Через площадь и диагонали
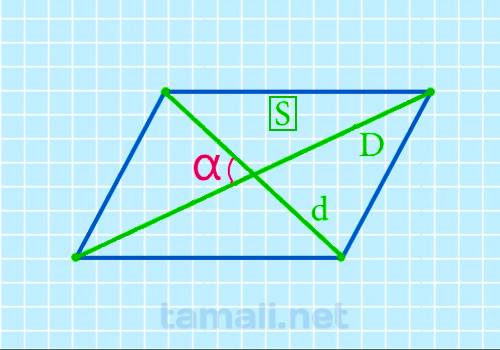
Для нахождения острого угла между диагоналями параллелограмма следует воспользоваться формулой:
sin α = 2S/(Dd)
где α – острый угол между диагоналями, S – площадь параллелограмма, D и d – его диагонали.
Цифр после
запятой:
Результат в:
Приведем пример расчета по формуле для наглядного случая, когда диагонали перпендикулярны, и площадь
данного ромба равняется половине площади прямоугольника, в который данный ромб можно вписать.
При D = 20 мм, d = 10 мм, площадь описанного прямоугольника равна 20*10=200 мм², откуда S = 200/2=100 мм².
Вычисления дают sin α = 2S/(Dd) = 2*100/(20*10) = 1, откуда α = 90°. Известный факт – диагонали
ромба перпендикулярны.
Через две стороны и диагонали
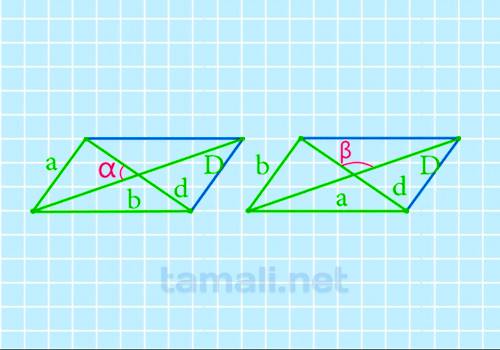
В предыдущей формуле угол определялся через диагонали и одну сторону, в данной задаче требуется
определить угол по диагоналям и 2 сторонам. Тем самым, одно из условий является избыточным, и фигура
по произвольным данным может не оказаться параллелограммом. Но для случая параллелограмма, т.е.
взаимной увязки данных, формулы таковы:
cos α = (b2-a2)/(Dd), cos β = (a2-b2)/(Dd)
где a и b – стороны параллелограмма, α и β – углы между диагоналями (взаимно дополнительные до
180°).
Цифр после
запятой:
Результат в:
Пример приведем по предыдущему случаю, остается только рассчитать недостающую сторону b, которая из
простых соображений (воспользовавшись правилом длины катета против угла в 30°) оказывается равной 20
мм. Вычисляем: cos α = (b²-a²)/(Dd) = (20²-34,64²)/(40*40) = -0,5, откуда
α = 120°.
Через диагонали и сторону
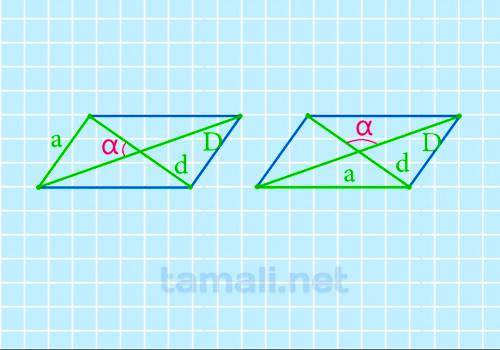
Для нахождения угла между диагоналями параллелограмма через диагонали и сторону формула такова:
cos α = (D² + d² – 4a²)/(2Dd)
где a – сторона параллелограмма, остальные обозначения прежние.
Цифр после
запятой:
Результат в:
Здесь следует считаться с тем, что если в предыдущей задаче угол по условию являлся острым, в данной
задаче он может быть и тупым, с отрицательным значением косинуса угла.
Пример расчета опять-таки по наглядному случаю, когда обе диагонали равны. Это прямоугольник с
диагоналями D = 40 мм и d = 40 мм. При угле между диагоналями 120° половина диагонали составит 40/2 = 20 мм, половина высоты прямоугольника (она же – половина короткой
стороны) составит половину от половины диагонали (в прямоугольном треугольнике противолежащий углу в
30° катет равен половине гипотенузы), т.е. 10 мм, откуда половина стороны параллелограмма составит
√(20²-10²)=√300=17,32 мм, а сторона параллелограмма a = 2*17,32=34,64 мм.
Подставляем в формулу: cos α = (D² + d² – 4a²)/(2Dd) = (40²+40²-4*34,642) = ‑1600/(2*40*40) = -0,5.
Значению косинуса -0,5 соответствует угол 120°. Это же значение даст и калькулятор.
Квадрат достаточно задать одним элементом – стороной. Для задания прямоугольника необходимо задать
уже две его смежные стороны; для ромба сторону и угол между сторонами. Для задания же
параллелограмма необходимо задание 3 его взаимно независимых элементов. Это могут быть 2 смежные
стороны и угол между ними, но возможно и иное задание.
В любом четырехугольнике можно провести 2 диагонали, и они также могут входить в набор элементов для
задания фигуры. В данной статье приводятся справочные формулы для определения угла между диагоналями
параллелограмма через другие его элементы. Рассчитать же этот угол для каждого из 3 рассматриваемых
случаев позволят калькуляторы сайта, в которые необходимо ввести известные элементы, и в результате
получить синус или косинус искомого угла либо сам угол в градусах или радианах.
Как найти угол между диагоналями параллелограмма
Прежде чем искать решение поставленной задачи, следует выбрать наиболее подходящий метод ее решения. Геометрический метод требует тдополнительных построений и их обоснования, поэтому в данном случае наиболее удобным представляется использование векторной методики. Для этого используются направленные отрезки – векторы.

Вам понадобится
- – бумага;
- – ручка;
- – линейка.
Инструкция
Пусть параллелограмм задан векторами двух его сторон (остальные две попарно равны) в соответствии с рис. 1. Вообще-то равных векторов на плоскости сколь угодно много. Для этого требуется равенство их длин (точнее модулей – |a|) и направления, которое задается наклоном к какой-либо оси (в декартовых координатах это ось 0Х). Поэтому для удобства в задачах подобного типа векторы, как правило, задают их радиус-векторами r=а, у которых начало всегда лежит в начале координат.
Для нахождения угла между сторонами параллелограмма понадобится вычислить геометрическую сумму и разность векторов, а также их скалярное произведение (a,b). По правилу параллелограмма геометрическая сумма векторов a и b равна некоторому вектору с=а+b, который построен и лежит на диагонали параллелограмма AD. Разность a и b – вектор d=b-a, построенный на второй диагонали BD. Если векторы заданы координатами, а угол между ними составляет ф, тогда их скалярное произведение – это число, равное произведению модулей векторов и cosф (см. рис1): (a, b) = |a||b|cos ф
В декартовых координатах если а={x1, y1} и b={x2, y2}, то (a, b) = x1y2 +x2y1. При этом скалярный квадрат вектора (а,а)=|a|^2=x1^2 +x2^2. Для вектора b – аналогично. Тогда: |a||b|cos ф = x1y2 +x2y1. Следовательно cosф=(x1y2 +x2y1)/(|a||b|). Таким образом алгоритм решения задачи состоит в следующем:1. Нахождение координат векторов диагоналей параллелограмма как векторов суммы и разности векторов его сторон с=а+b и d=b-a. При этом соответствующие координаты a и b просто складываются или вычитаются. c= a+ b ={x3, y3}= { x1+x2, y1+y2},d= b-a ={x4, y4}={ x2 –x1, y2-y1}. 2. Нахождение косинуса угла между векторами диагоналей (назовем его фД) по приведенному общему правилу cosфд=(x3y3 +x4y4)/(|c||d|)
Пример. Найти угол между диагоналями параллелограмма, заданного векторами своих сторон a={1, 1} и b ={1, 4}. Решение. Согласно приведенному алгоритму вам необходимо найти векторы диагоналей c={1+1, 1+4}={2, 5} и d={1-1, 4-1}={0, 3}. Теперь вычислите cosфд =(0+15)/(sqrt(4+25)sqrt9)= 15/3sqrt29=0,92. Ответ: фд= arcos(0,92).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
