Наименьшая сумма чисел: как найти и зачем это нужно
Наименьшая сумма чисел – это минимальная сумма, которую можно получить при сложении элементов из двух или более различных множеств чисел. Важность этого понятия заключается в том, что оно является основой для решения многих математических и практических задач. В этой статье мы познакомимся с наименьшей суммой чисел, методами поиска и примерами использования в реальной жизни.
Что такое наименьшая сумма чисел?
Наименьшая сумма чисел – это минимальная сумма, которую можно получить при сложении чисел из двух или более различных множеств чисел. Проще говоря, это сумма, которую можно получить, выбрав по одному числу из каждого множества и сложив их вместе. Задача поиска наименьшей суммы чисел может быть сформулирована следующим образом: даны n множеств чисел, найти минимальную сумму, используя по одному числу из каждого множества.
Как найти наименьшую сумму чисел?
Существует несколько методов поиска наименьшей суммы чисел. Рассмотрим два основных подхода:
- Полный перебор: этот метод заключается в переборе всех возможных комбинаций чисел из разных множеств и нахождении минимальной суммы. Он является самым простым и надежным способом, но требует много времени и вычислительных ресурсов, особенно для больших множеств чисел.
- Жадные алгоритмы: жадный алгоритм выбирает на каждом шаге локально наилучший выбор с целью получить глобально оптимальное решение. Однако этот подход не всегда приводит к оптимальному решению. В случае наименьшей суммы чисел, жадный алгоритм может заключаться в выборе минимального числа из каждого множества и их сложении. Это может привести к достаточно быстрому решению, но не гарантирует, что найденная сумма будет действительно наименьшей.
- Динамическое программирование: это метод, который использует разделение задачи на подзадачи и сохраняет результаты подзадач для повторного использования. В случае наименьшей суммы чисел, динамическое программирование может быть использовано для решения задачи с меньшими временными затратами и вычислительными ресурсами по сравнению с полным перебором. Однако этот подход может быть сложнее для понимания и реализации.
Применение наименьшей суммы чисел в реальной жизни и математических задачах
Наименьшая сумма чисел играет важную роль в различных областях, таких как оптимизация, планирование и решение математических задач. Вот несколько примеров использования наименьшей суммы чисел:
- Транспортные задачи: наименьшая сумма чисел может использоваться для определения оптимального маршрута между несколькими пунктами назначения с целью минимизации затрат на транспортировку.
- Задачи распределения ресурсов: в бизнесе и экономике наименьшая сумма чисел может быть использована для определения оптимального распределения ресурсов между различными проектами или задачами с целью минимизации общих затрат.
- Задачи о назначениях: в этом случае наименьшая сумма чисел применяется для определения оптимального соответствия между элементами двух множеств, например, назначения работников на задачи или студентов на курсы, с целью минимизации общих затрат или усилий.
В заключение, наименьшая сумма чисел является важным понятием в математике и имеет широкое применение в реальной жизни. Овладение методами нахождения наименьшей суммы чисел позволяет эффективно решать различные задачи, связанные с оптимизацией, планированием и распределением ресурсов. Хотя существует несколько методов для нахождения наименьшей суммы чисел, таких как полный перебор, жадные алгоритмы и динамическое программирование, выбор подхода зависит от сложности задачи и доступных вычислительных ресурсов.
Советы для практики и дополнительные материалы
Чтобы развить навыки нахождения наименьшей суммы чисел, рекомендуется выполнить следующие шаги:
- Изучить основы комбинаторики и теории графов, которые помогут понять принципы работы методов поиска наименьшей суммы чисел.
- Попрактиковаться в решении задач, связанных с наименьшей суммой чисел, используя различные методы, чтобы определить их преимущества и недостатки.
- Изучить алгоритмы и структуры данных, такие как динамическое программирование, жадные алгоритмы и теорию графов, которые могут быть использованы для решения задач на наименьшую сумму чисел.
|
Argentum21 1 / 1 / 1 Регистрация: 05.03.2014 Сообщений: 75 |
|
|
1 |
|
Найти наименьшую по модулю сумму10.06.2014, 13:44. Показов 772. Ответов 0 Метки нет (Все метки)
Даны натуральное число n и действительные числа a1,…,an. Ни одно из чисел a1,…,an не равно нулю. Найти наименьшее по модулю из всех значений вида ai+aj+…+ap, гдe 1<=i<j<…<p<=n.
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
10.06.2014, 13:44 |
|
Ответы с готовыми решениями:
МАСИИВЫ, найти сумму каждого рядка матрицы та наименьшую из них! не могу другую часть программы сделать.. int main() 0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
10.06.2014, 13:44 |
|
Помогаю со студенческими работами здесь
Массивы. Найти минимальный по модулю элемент массива. Найти сумму модулей элементов после первого нуля
Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 1 |
Доказательства свойств модуля
☰
Существуют следующие свойства модуля действительных чисел:
1) |a + b| ≤ |a| + |b|;
2) |ab| = |a| × |b|;
3) , a ≠ 0;
4) |a – b| ≥ |a| – |b|.
Проведем доказательства, рассматривая различные случаи значений a и b.
Доказательство 1) |a + b| ≤ |a| + |b|:
Если a и b – положительные числа, то их модули совпадают с их значениями: |a| = a, |b| = b. Из этого следует, что |a + b| = |a| + |b|.
Если a – отрицательное число, а b – положительное число, то выражение |a + b| можно записать как |b – a|. Выражение же |a| + |b| равно сумме абсолютных значений a и b, что больше, чем b – a. Поэтому |a + b| < |a| + |b|.
Если b – отрицательное число, а a – положительное, то |a + b| принимает вид |a – b|, что также меньше суммы модулей |a| + |b|.
Если a и b – отрицательные числа, то получим |–a – b|. Результат этого выражения равен |a + b| (т.
к. |–a – b| = |–(a + b)| = |a + b|). Но уже было доказано, что |a + b| = |a| + |b|, следовательно и |–a – b| = |a| + |b|.
Доказательство 2) |ab| = |a| × |b|:
Здесь, в отличие от сложения, рассматривать все случаи особо не требуется, т. к. абсолютное значение произведения любых чисел (положительных ли, отрицательных ли) не зависит от знаков множителей. В выражении |ab| мы сначала перемножаем числа, а потом «отбрасываем» знак (отрицательный, если он есть), в выражении |a| × |b| сначала избавляемся от знаков, а потом перемножаем. Но от того, в какой момент был взят модуль (до или после умножения), не зависит абсолютное значение произведения.
Доказательство 3) , a ≠ 0:
Если a – положительное число, то |a| = a и, следовательно, доказываемое равенство верно, т. к. и правая и левая части равны 1/a.
Если a – отрицательное число, то имеем . Взятие модуля в обоих выражениях приведет к делению единицы на абсолютное значение a.
2-1}{4}d$. Равенство в нем достигается, когда $a_1 = ldots = a_m lt a_{m+1} = ldots = a_{2m+1}$.
Поделиться ссылкой:
Похожее
Внеклассный урок — Модуль числа
Модуль числа
Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Например, модулем числа 5 является 5, модулем числа –5 тоже является 5.
То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.
Обозначается так: |5|, |х|, |а| и т.д.
Правило:
|а| = а, если а ≥ 0.
|а| = –а, если а < 0.
Пояснение:
|5| = 5
Читается так: модулем числа 5 является 5.
|–5| = –(–5) = 5
Читается так: модулем числа –5 является 5.
|0| = 0
Читается так: модулем нуля является ноль.
Свойства модуля:
1) Модуль числа есть неотрицательное число:
|а| ≥ 0
2) Модули противоположных чисел равны:
|а| = |–а|
3) Квадрат модуля числа равен квадрату этого числа:
|а|2 = a2
4) Модуль произведения чисел равен произведению модулей этих чисел:
|а · b| = |а| · |b|
6) Модуль частного чисел равен отношению модулей этих чисел:
|а : b| = |а| : |b|
7) Модуль суммы чисел меньше или равен сумме их модулей:
|а + b| ≤ |а| + |b|
8) Модуль разности чисел меньше или равен сумме их модулей:
|а – b| ≤ |а| + |b|
9) Модуль суммы/разности чисел больше или равен модулю разности их модулей:
|а ± b| ≥ ||а| – |b||
10) Постоянный положительный множитель можно вынести за знак модуля:
|m · a| = m · |а|, m >0
11) Степень числа можно вынести за знак модуля:
|аk| = |а|k, если аk существует
12) Если |а| = |b|, то a = ± b
Геометрический смысл модуля.
Модуль числа – это величина расстояния от нуля до этого числа.
Для примера возьмем снова число 5. Расстояние от 0 до 5 такое же, что и от 0 до –5 (рис.1). И когда нам важно знать только длину отрезка, то знак не имеет не только значения, но и смысла. Впрочем, не совсем верно: расстояние мы измеряем только положительными числами – или неотрицательными числами. Пусть цена деления нашей шкалы составляет 1 см. Тогда длина отрезка от нуля до 5 равна 5 см, от нуля до –5 тоже 5 см.
На практике часто расстояние отмеряется не только от нуля – точкой отсчета может быть любое число (рис.2). Но суть от этого не меняется. Запись вида |a – b| выражает расстояние между точками а и b на числовой прямой.
Пример 1. Решить уравнение |х – 1| = 3.
Решение.
Смысл уравнения в том, что расстояние между точками х и 1 равно 3 (рис.2). Поэтому от точки 1 отсчитываем три деления влево и три деления вправо – и наглядно видим оба значения х:
х1 = –2, х2 = 4.
Можем и вычислить.
│х – 1 = 3
│х – 1 = –3
↕
│х = 3 + 1
│х = –3 + 1
↕
│х = 4
│ х = –2.
Ответ: х1 = –2; х2 = 4.
Пример 2. Найти модуль выражения:
3√5 – 10.
Решение.
Сначала выясним, является ли выражение положительным или отрицательным. Для этого преобразуем выражение так, чтобы оно состояло из однородных чисел. Не будем искать корень из 5 – это довольно сложно. Поступим проще: возведем в корень 3 и 10. Затем сравним величину чисел, составляющих разность:
3 = √9. Следовательно, 3√5 = √9 · √5 = √45
10 = √100.
Мы видим, что первое число меньше второго. Значит, выражение отрицательное, то есть его ответ меньше нуля:
3√5 – 10 < 0.
Но согласно правилу, модулем отрицательного числа является это же число с противоположным знаком. У нас отрицательное выражение. Следовательно, надо поменять его знак на противоположный. Выражением, противоположным 3√5 – 10, является –(3√5 – 10). Раскроем в нем скобки – и получим ответ:
Следовательно, надо поменять его знак на противоположный. Выражением, противоположным 3√5 – 10, является –(3√5 – 10). Раскроем в нем скобки – и получим ответ:
–(3√5 – 10) = –3√5 + 10 = 10 – 3√5.
Ответ:
|3√5 – 10| = 10 – 3√5.
Модуль — сумма — Большая Энциклопедия Нефти и Газа, статья, страница 1
Модуль — сумма
Cтраница 1
Модуль суммы не может превзойти сумму модулей слагаемых.
[1]
Модуль суммы двух или нескольких комплексных чисел не превосходит суммы модулей этих чисел.
[2]
Модуль суммы двух или нескольких чисел меньше или равен сумме модулей этих чисел.
[3]
Модуль суммы индексов всех особых точек невырожденного векторного поля v степени т ( обозначается Ind v) не превосходит числа Петровского — — Олейник II ( т) и сравним по модулю 2 с числом и.
Никаких других ограничений на Irul v не существует.
[4]
Заменим модуль суммы в правой части ( 20) суммой модулей и потребуем выполнения полученного неравенства. В этом случае ( 20) будет выполняться автоматически.
[5]
Докажите, что модуль суммы двух перемещений не превосходит суммы модулей составляющих перемещений. В каком случае модуль суммы равен сумме модулей слагаемых перемещений.
[6]
Известно, что модуль суммы меньше или равен сумме модулей слагаемых.
[7]
Доказать, что модуль суммы двух комплексных чисел не превосходит суммы модулей этих чисел.
[8]
Установим теперь свойства
модуля суммы и разности двух комплексных чисел.
[9]
Теорема о том, что модуль суммы не больше суммы модулей слагаемых, легко распространяется на случай абсолютно сходящихся рядов.
[10]
Теорема о том, что модуль суммы не больше суммы модулей слагаемых, легко распространяется на случай абсолютно сходящихся рядов.
[11]
Поскольку разложить в ряд Фурье модуль суммы гармоник в общем виде нельзя, укажем, что при незначительных искажениях несущей выходной сигнал будет подобен детектированному.
[12]
Принципиальный интерес представляет способ выделения модуля суммы и разности входных — величин, предложенный в.
[13]
Установим теперь важные для дальнейшего свойства модуля суммы и разности двух комплексных чисел.
[14]
Такое отображение, фактически представляющее собой натягивание модуля суммы гауссовскнх полей на параболоиды в направлении внешней нормали, переведет гладкие параболоиды в некоторые случайные геометрические тела. {2}}Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end{array})
{2}}Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end{array})
а это противоречит определению модуля.
Следовательно, таких ( x;yin mathbb{R}) не существует, а значит, при всех ( x,text{ }yin mathbb{R}) выполняется неравенство ( left| x+y right|le left| x right|+left| y right|.)
Примеры для самостоятельного решения:
1) Докажите свойство
№6.
2) Упростите выражение ( left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|).
Ответы:
1) Воспользуемся свойством №3: ( left| ccdot x right|=left| c right|cdot left| x right|), а поскольку ( c>0text{ }Rightarrow text{ }left| c right|=c), тогда
( left| cx right|=ccdot left| x right|), ч.т.д.
2) ( left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|). {2}}overset{<}{mathop{vee }},15cdot 16text{ }Rightarrow text{ })
{2}}overset{<}{mathop{vee }},15cdot 16text{ }Rightarrow text{ })
( frac{15}{4}-sqrt{15}text{ }<0text{ }Rightarrow text{ }left| frac{15}{4}-sqrt{15} right|=sqrt{15}-frac{15}{4}).
Складываем значения модулей:
( displaystyle left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|=frac{31}{8}-sqrt{15}+sqrt{15}-frac{15}{4}=frac{1}{8}=0.125)
В уравнении сумма равна 0
Мы уже рассматривали уравнения, равные нулю (типа «произведение равно нулю»). К виду «произведение равно нулю» сводятся многие уравнения из разных разделов алгебры.
Если в уравнении сумма равна нулю, в некоторых случаях его можно решить, применяя следующее свойство функций:
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда каждая из функций равна нулю.
Таким образом, уравнение
где
равносильно системе уравнений
В частности,
где 2n — чётное натуральное число
Примеры уравнений, решение которых основано на этом свойстве функций.
ОДЗ: x∈R.
Сумма модулей равна нулю, если каждое из слагаемых равно нулю. Поэтому данное уравнение равносильно системе
Найдём корни каждого уравнения:
Оба модуля обращаются в нуль при x=2.
Ответ: 2.
ОДЗ: x∈[-4;2].
Сумма корней чётной степени равна нулю, если каждое из слагаемых рано нулю. Следовательно, это уравнение равносильно системе
Решаем каждое уравнение:
Оба слагаемых обращаются в нуль при x= -4.
Ответ: -4.
Для нахождения корней достаточно решить только одно из уравнений и проверить, удовлетворяют ли полученные корни остальным уравнениям системы.
ОДЗ: x∈(-∞; 1]U[9; ∞).
Сумма неотрицательных функций равна нулю, если каждая каждая из функций равна нулю:
Корень третьего уравнения — x=9 — удовлетворяет также 1-му и 2-му уравнениям системы.
Ответ: 9.
ОДЗ: x∈[-1; 1].
Правая часть уравнений — сумма неотрицательных функций. Соответственно, уравнение равносильно системе
Корни второго уравнения
x=1 и x= -1. Оба корня удовлетворяют и первому уравнению.
Ответ: ±1.
Как в другие уравнения из курса алгебры, решаемые с применением свойств функций, уравнения, в которых сумма неотрицательных функций равна нулю, при первом рассмотрении могут производить впечатление сложных. На самом деле, решить их достаточно просто, если помнить соответствующий теоретический материал.
Сумма модулей отклонений — Студопедия
плюсы:
— нечувствительность к выбросам.
минусы:
— сложность вычислительной процедуры;
— возможность больших отклонений между фактическими и проектными функциями;
— неоднозначность значений параметров и т.д.
Исходя из этих преимуществ и недостатков, обычно в качестве меры близости выбирают сумму квадратов и выбирают такую функцию
y=f(x), у которой эта сумма квадратов достигает минимума.
Для того, чтобы лучше понять сущность метода наименьших квадратов, необходимо вначале вспомнить математические основы определения экстремума функции нескольких переменных.
В первую очередь, введем некоторые определения:
Определение 1.Функция Z = ƒ (x, y)имеет максимум в точке М0 (х0, у0), если значение функции в этой точке больше значений ее в точках, достаточно близких к точке М0 (х0, у0), т.е.
ƒ (х0, у0) > ƒ (х0 + Δх, у0 + Δу).
Это означает, что полное приращение функции Z = ƒ (х, у), вызванное переходом от точки (х0, у0) к соседней точке, будет величиной отрицательной:
ΔZ = ƒ (х0 + Δх, у0
+ Δу) — ƒ (х0, у0) < 0. (2.1)
Определение 2.Функция Z = ƒ (x, y)имеет минимум в точке М0 (х0, у0), если значение функции в этой точке меньше значений ее в точках, достаточно близких к точке М0 (х0, у0), т. е.
е.
ƒ (х0, у0) < ƒ (х0 + Δх, у0 + Δу).
Это означает, что полное приращение функции Z = ƒ (х, у), будет величиной положительной:
ΔZ = ƒ (х0 + Δх, у0 + Δу) — ƒ (х0, у0) > 0. (2.2)
Допустим, что функция Z = ƒ (х, у) имеет в точке М0 (х0, у0) максимум или минимум (экстремум).Тогда для функции должно выполняться одно из неравенств (3.1) или (3.2) при любых, достаточно малых Δх, Δу.
Предположим, что Δу = 0; тогда функция Z = ƒ (х, у) сделается функцией только одной переменной х. Эта функция по условию имеет экстремум.
Таким образом, условия обращения в нуль частных производных функции или несуществование хотя бы одной из них являются необходимыми условиями, но недостаточными условиями экстремума функции.
Имеем систему:
. (2.4)
Условия (2. 4) являются необходимыми для существования экстремума функции. Но может случиться, что эти условия в некоторых обстоятельствах невыполнимы.
4) являются необходимыми для существования экстремума функции. Но может случиться, что эти условия в некоторых обстоятельствах невыполнимы.
Достаточные условия существования экстремума функции нескольких переменных имеют более сложный вид.
Пусть в точке М0 (х0, у0) частные производные обращаются в нуль, т.е.
, .
Подсчитаем значения частных производных второго порядка функции
Z = ƒ (х, у) в этой точке и обозначим их соответственно буквами: А, В, С:
тогда:
1. Если АС — В2 > 0, то функция Z = ƒ (х, у) имеет в точке М0 (х0, у0) экстремум, а именно:
при А < 0 максимум,
при А > 0 минимум.
2. Если АС — В2 < 0, то функция Z = ƒ (х, у) не имеет в точке М0 (х0, у0) экстремума.
3. Если АС — В2 = 0, то вопрос о существовании экстремума функции в точке М0 (х0, у0) остается открытым и требуются дополнительные исследования.
Метод наименьших квадратов является одним из важных применений теории экстремума функции нескольких переменных.
Предположим, что в результате некоторого опыта или наблюдения установлена зависимость между переменными величинами х и у, выражаемая в виде таблицы:
| х | х1 | х2 | … | хn |
| у | у1 | у2 | … | уn |
Пусть требуется перейти от табличного метода задания функции к аналитическому (т.е. выраженному в виде формулы), причем, если это нельзя сделать точно, постараемся получить аналитическую связь приближенно.
Теперь обратимся к графическому изображению данной системы. Рассматривая значения х и у как координаты точек в прямоугольной системе координат, наносим эти точки на график. Пусть, например, построенные точки расположены достаточно близко к некоторой прямой. Поэтому можно приблизительно считать, что между х и у существует линейная зависимость, выражаемая формулой,
Поэтому можно приблизительно считать, что между х и у существует линейная зависимость, выражаемая формулой,
у = ах + b.
Поставим задачу аналитического определения неизвестных коэффициентов а и b.
В основе аналитического метода определения а и b лежит метод наименьших квадратов. Точки, полученные на основании опытных данных, вообще говоря, не лежат на искомой прямой. Если бы некоторая точка (хi, уi) лежала на прямой, то ее координаты удовлетворяли бы уравнению прямой, т.е. имело бы место равенство:
уi = axi + b или axi + b — yi = 0
Однако в общем случае подстановка координат точки в уравнение прямой дала бы:
axi + b — yi = εi,
где εi ─ какая то малая величина.
Прямая сумма модулей — Примеры задач
В абстрактной алгебре прямая сумма — это конструкция, которая объединяет несколько модулей в новый, более крупный. В некотором смысле прямая сумма модулей — это «самый общий» модуль, который содержит данные модули как подпространства.
В некотором смысле прямая сумма модулей — это «самый общий» модуль, который содержит данные модули как подпространства.
Наиболее известные примеры этой конструкции встречаются при рассмотрении векторных пространств (модулей над полем) и абелевых групп (модулей над кольцом Z целых чисел). Конструкция также может быть расширена для покрытия банаховых и гильбертовых пространств.
Конструкция векторных пространств и абелевых групп
Мы даем конструкцию первой в этих двух случаях в предположении, что у нас есть только два объекта. Затем мы обобщаем на произвольное семейство произвольных модулей. Ключевые элементы общей конструкции более четко определяются при более глубоком рассмотрении этих двух случаев.
Конструкция для двух векторных пространств
Предположим, что V и W — векторные пространства над полем K .Мы можем превратить декартово произведение V × W в векторное пространство над K , определив операции покомпонентно:
- ( v 1 , w 1 ) + ( v 2 , w 2 ) = ( v 1 + v 2 , ш 1 + ш 2 )
- α ( v , w ) = (α v , α w )
для v , v 1 , v 2 дюймов V , w , w 1 , w 2 в W и α в K .
Результирующее векторное пространство называется прямой суммой V и W и обычно обозначается знаком плюса внутри круга:
- V⊕W { displaystyle V oplus W}
Подпространство V × {0} V ⊕ W изоморфно V и часто идентифицируется с V ; аналогично для {0} × W и W . (См. Внутреннюю прямую сумму ниже.) При такой идентификации верно, что каждый элемент V ⊕ W может быть записан одним и только одним способом как сумма элемента V и элемента W . Размер V ⊕ W равен сумме размеров V и W .
Эта конструкция легко обобщается на любое конечное число векторных пространств.
Конструкция для двух абелевых групп
Для абелевых групп G и H , которые записываются аддитивно, прямое произведение также называется прямой суммой.Таким образом, мы превращаем декартово произведение G × H в абелеву группу, определяя операции покомпонентно:
- ( г 1 , ч 1 ) + ( г 2 , ч 2 ) = ( г 1 + г 2 , h 1 + h 2 )
для г 1 , г 2 дюймов G и h 1 , h 2 дюймов Н .
Обратите внимание, что мы также можем расширить операцию взятия целых кратных до прямой суммы:
для г в G , h в H и n целое число. Это аналогично расширению скалярного произведения векторных пространств до указанной выше прямой суммы.
Результирующая абелева группа называется прямой суммой из G и H и обычно обозначается знаком плюса внутри круга:
- G⊕H { displaystyle G oplus H}
Подпространство G × {0} из G ⊕ H изоморфно G и часто идентифицируется с G ; аналогично для {0} × H и H .(См. Внутреннюю прямую сумму ниже.) С этой идентификацией верно, что каждый элемент G ⊕ H может быть записан одним и только одним способом как сумма элемента G и элемента из H . Ранг G ⊕ H равен сумме рангов G и H .
Эта конструкция легко обобщается на любое конечное число абелевых групп.
Построение произвольного семейства модулей
Следует заметить явное сходство между определениями прямой суммы двух векторных пространств и двух абелевых групп.Фактически каждый из них является частным случаем построения прямой суммы двух модулей. Кроме того, изменяя определение, можно учесть прямую сумму бесконечного семейства модулей. Точное определение выглядит следующим образом.
Предположим, что R — некоторое кольцо, а { M i : i in I } — семейство левых модулей R , индексированных набором I . Прямая сумма для { M i } затем определяется как набор всех функций α с областью I , таких что α ( i ) ∈ M i для все i ∈ I и α ( i ) = 0 для всех, кроме конечного числа индексов i .
Две такие функции α и β можно добавить, записав (α + β) ( i ) = α ( i ) + β ( i ) для всех i (обратите внимание, что это снова ноль для все, кроме конечного числа индексов), и такая функция может быть умножена на элемент r из R , записав ( r α) ( i ) = r (α ( i )) для все и . Таким образом, прямая сумма становится левым модулем R . Обозначим его через
Таким образом, прямая сумма становится левым модулем R . Обозначим его через
- ⨁i∈IMi { displaystyle bigoplus _ {i in I} M_ {i}}
Свойства
При правильной идентификации мы снова можем сказать, что каждый элемент x прямой суммы может быть записан одним и только одним способом как сумма конечного числа элементов M i .
Если M i на самом деле являются векторными пространствами, то размерность прямой суммы равна сумме размеров M i . То же верно и для ранга абелевых групп и длины модулей.
Каждое векторное пространство над полем K изоморфно прямой сумме достаточно большого количества копий K , поэтому в определенном смысле следует учитывать только эти прямые суммы. Это неверно для модулей над произвольными кольцами.
Тензорное произведение распределяется по прямым суммам в следующем смысле: если N — некоторый правильный R -модуль, то прямая сумма тензорных произведений N на M i (что являются абелевыми группами) естественно изоморфно тензорному произведению N на прямую сумму M i .
Прямые суммы также коммутативны и ассоциативны, что означает, что не имеет значения, в каком порядке формируется прямая сумма.
Группа линейных гомоморфизмов R из прямой суммы в некоторую левую R -модуль L естественно изоморфна прямому произведению групп R -линейных гомоморфизмов из M i до L .
Внутренняя прямая сумма
Предположим, что M — это некий модуль R , а M i — это подмодуль M для каждых i в I .Если каждое x в M может быть записано одним и только одним способом как сумма конечного числа элементов M i , то мы говорим, что M — это внутренняя прямая сумма субмодулей M i . В этом случае M естественно изоморфна (внешней) прямой сумме M i , как определено выше.
Прямое слагаемое из M — это подмодуль N , такой, что есть другой подмодуль N ‘ из M , такой, что M является внутренней внутренней прямой суммой N и N ′ .
Категориальная интерпретация
На языке теории категорий прямая сумма является копроизведением и, следовательно, копределом в категории левых R -модулей, что означает, что она характеризуется следующим универсальным свойством. Для каждых i в I учитывайте естественное вложение
- ji: Mi → ⨁i∈IMi { displaystyle j_ {i}: M_ {i} rightarrow bigoplus _ {i in I} M_ {i}}
, который отправляет элементы M i к тем функциям, которые равны нулю для всех аргументов, кроме i .Если f i : M i → M являются произвольными линейными картами R для каждого i , то существует ровно одна линейная карта R
- f: ⨁i∈IMi → M { displaystyle f: bigoplus _ {i in I} M_ {i} rightarrow M}
, так что f o j i = f i для всех i .
Прямая сумма модулей с дополнительной структурой
Если рассматриваемые нами модули несут некоторую дополнительную структуру (например,грамм. норма или внутренний продукт), то прямая сумма модулей часто также может содержать эту дополнительную структуру. В этом случае мы получаем копродукт в соответствующей категории всех объектов, несущих дополнительную структуру. Два наиболее ярких примера относятся к банаховым и гильбертовым пространствам.
Прямая сумма банаховых пространств
Прямая сумма двух банаховых пространств X и Y является прямой суммой X и Y , рассматриваемых как векторные пространства, с нормой || ( x , y ) || = || x || X + || y || Y для всех x дюймов X и y дюймов Y .
Как правило, если X i , где i пересекает набор индексов I , представляет собой набор банаховых пространств, то прямая сумма ⊕ i ∈ I X i состоит из всех функций x с доменом I , так что x ( i ) ∈ X i для всех i ∈ I и
- ∑i∈I‖x (i) ‖Xi конечно.
 { displaystyle sum _ {i in I} | x (i) | _ {X_ {i}} { mbox {конечно.}}}
{ displaystyle sum _ {i in I} | x (i) | _ {X_ {i}} { mbox {конечно.}}}
Норма определяется суммой выше. Прямая сумма с этой нормой снова является банаховым пространством.
Например, если мы возьмем набор индексов I = N и X i = R , то прямая сумма ⊕ i ∈ N будет пробелом l 1 , который состоит из всех последовательностей ( a i ) вещественных чисел с конечной нормой || a || = ∑ i | a i |.
Прямая сумма гильбертовых пространств
Если дано конечное число гильбертовых пространств H 1 , …, H n , можно построить их прямую сумму, как указано выше (поскольку они являются векторными пространствами), а затем повернуть прямую сумму в гильбертово пространство, определив внутренний продукт как:
- ⟨(x1, .
 .., xn), (y1, …, yn)⟩ = ⟨x1, y1⟩ + … + ⟨xn, yn⟩ { displaystyle langle (x_ {1}, …, x_ {n}), (y_ {1}, …, y_ {n}) rangle = langle x_ {1}, y_ {1} rangle +… + langle x_ {n}, y_ {n} rangle}
.., xn), (y1, …, yn)⟩ = ⟨x1, y1⟩ + … + ⟨xn, yn⟩ { displaystyle langle (x_ {1}, …, x_ {n}), (y_ {1}, …, y_ {n}) rangle = langle x_ {1}, y_ {1} rangle +… + langle x_ {n}, y_ {n} rangle}
Это превращает прямую сумму в гильбертово пространство, которое содержит данные гильбертовы пространства как взаимно ортогональные подпространства.
Если дано бесконечно много гильбертовых пространств H i для i в I , мы можем провести такое же построение; обратите внимание, что при определении внутреннего продукта только конечное число слагаемых будет отличным от нуля. Однако результатом будет только внутреннее пространство продукта, и оно не будет полным.Затем мы определяем прямую сумму гильбертовых пространств H i как завершение этого внутреннего пространства продукта.
В качестве альтернативы и эквивалентно, можно определить прямую сумму гильбертовых пространств H i как пространство всех функций α с областью I , так что α ( i ) является элементом H i для каждых i в I и:
- ∑i‖α (я) ‖2 <1 { displaystyle sum _ {i} left | alpha _ {(i)} right | ^ {2} <{ mathcal {1}} }
Тогда скалярное произведение двух таких функций α и β определяется как:
- ⟨α, β⟩ знак равно ∑i⟨αi, βi⟩ { displaystyle langle alpha, beta rangle = sum _ {i} langle alpha _ {i}, beta _ {i} rangle}
Это пространство заполнено, и мы получаем гильбертово пространство.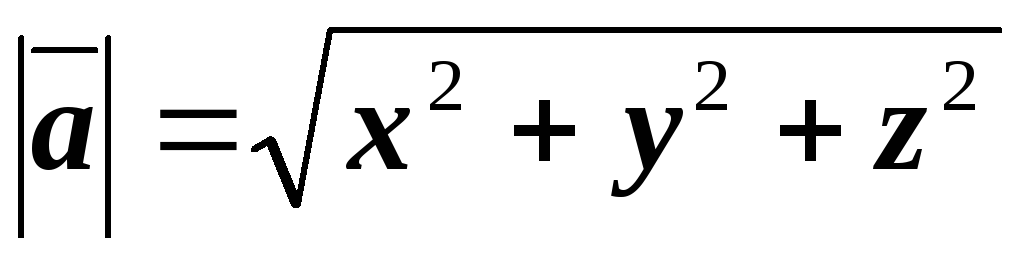 {2}}. Сравнивая это с примером для банаховых пространств, мы видим, что прямая сумма банахова пространства и прямая сумма гильбертова пространства не обязательно совпадают. Но если имеется только конечное число слагаемых, то прямая сумма банахова пространства изоморфна прямой сумме гильбертова пространства.
{2}}. Сравнивая это с примером для банаховых пространств, мы видим, что прямая сумма банахова пространства и прямая сумма гильбертова пространства не обязательно совпадают. Но если имеется только конечное число слагаемых, то прямая сумма банахова пространства изоморфна прямой сумме гильбертова пространства.
Каждое гильбертово пространство изоморфно прямой сумме достаточно большого числа копий основного поля (либо R , либо C ).
de: Direkte Summe
es: Suma directa
fr: somme directe
он: סכום ישר
ja: 直 和
(PDF) Подмодули типов и разложение модулей по прямой сумме
98 J.DAUNS AND Y. ZHOU
(4) ⇒ (2). Пусть K — естественный класс. Чтобы показать (2), достаточно показать
, что для любых подмодулей X и Y из M, если X и Yare в K, тогда
будет X + Y. По лемме Цорна существует подмодуль Pmaximal
относительно X⊆P∈K и подмодуль Qmaximal относительно
до Y⊆Q∈K. Тогда P и Q дополняют подмодули M,
P∩Q≤eP и P∩Q ≤eQ.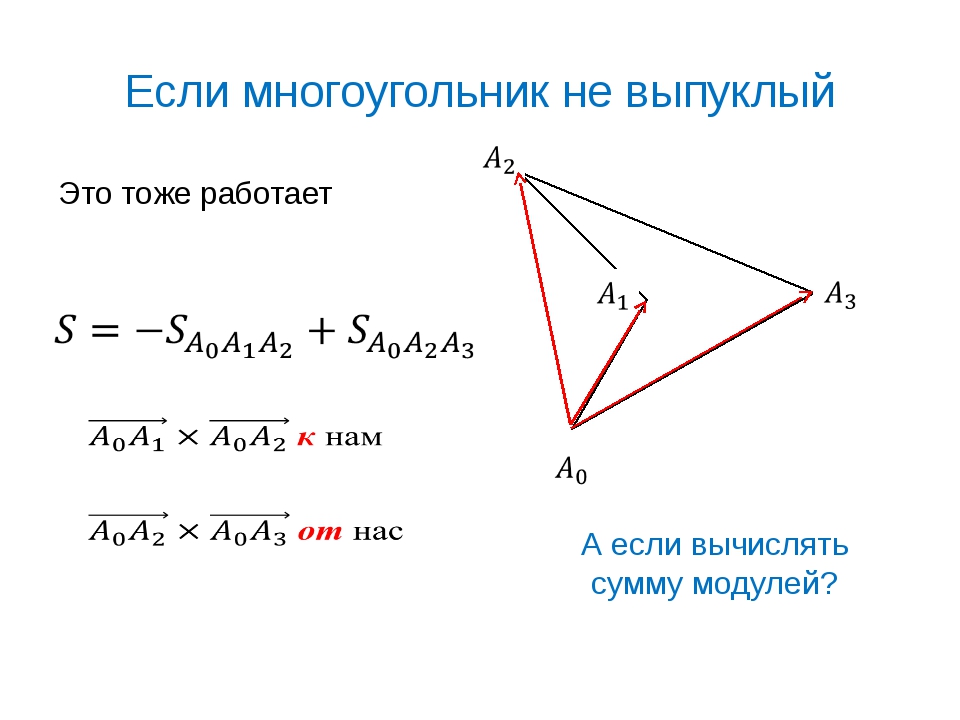 Таким образом, P и Q оба являются замыканиями
Таким образом, P и Q оба являются замыканиями
P∩Qin M. Если P = Q, по (4) существует 0– = X⊆P + Q, например
P∩X = 0 и X → P∩Q.Тогда X∈K и P⊂P⊕X∈K, противоречие
. Итак, P = Q и, значит, X + Y⊆P∈K.
(5) ⇒ (1). Предположим, что (1) не выполняется. Тогда существуют подмодули типа
T1- = T2 Mof типа K для естественного класса K. Отсюда следует
, что T1∩T2- = 0, T1∩T2≤eTifor i = 1,2, и T1∩T2 не является существенным
. в T1 + T2. Таким образом, существует 0 = A⊆T1 + T2, такое что
T1∩T2∩A = 0. Отсюда следует, что Ti∩A = 0fori = 1,2. Поскольку
каждый Ti является подмодулем типа M, мы имеем TiTA. Мы знаем, что
A = A / (T1∩A) ∼
= (A + T1) / T1⊆ (T2 + T1) / T1∼
= Т2 / (Т1∩Т2).Тогда
A∼
= B / (T1∩T2) для некоторого B с T1∩T2≤eB⊆T2. Обратите внимание, что B⊥A,
и поэтому B∩A = 0 иB⊕A⊆M.
(3) ⇒ (5). Предположим, что существует вложение X⊕ (X / Y) α
→ M
, где Y — собственный существенный подмодуль X и X⊥ (X / Y). Возьмем
Возьмем
x∈X, но x / ∈Y, и пусть m1 = α (x) и m2 = α (x + Y). Тогда m1R⊥
m2R. Чтобы в этом убедиться, пусть m1aR ∼
= m2bR для некоторых a, b ∈R. Отсюда следует, что
α (xaR) ∼
= α ((x + Y) bR). Это дает xaR ∼
= (x + Y) bR.Должно быть
xaR = 0, поскольку X⊥ (X / Y). Итак, m1aR = 0. Таким образом, m1R⊥m2R.
Кроме того, m⊥
1⊆m⊥
2 и m⊥
2 / m⊥
1≤eR / m⊥
1.Wenextprovem2 = 0,
, что дает противоречие. Определим β: m1R → m2R по β (m1r) = m2r,
r∈R. Тогда β является гомоморфизмом и ker (β) = m1m⊥
2. Пусть L будет замыканием типа
для ker (β) inm1R. Определим f: m1R → m1R⊕m2R (⊆M)
как f (x) = x + β (x), x∈m1R. Тогда это мономорфизм. Поскольку L
является замыканием типа ker (β) inm1R, f (ker (β)) параллельно f (L).Это
дает, что ker (β) параллельно f (L). Пусть Ltc и f (L) tc — замыкания типа
Земли f (L) inM соответственно. Тогда и Ltc, и f (L) tc
Тогда и Ltc, и f (L) tc
являются замыканиями типа ker (β) в M. По (3) Ltc = f (L) tc. Отсюда следует, что
L + f (L) является параллельным расширением L.ПримечаниеL — это подмодуль типа
m1R. Так как m1R⊥m2R, Lis — подмодуль типа для m1R⊕m2R. Это
означает, что L = L + f (L), т. Е. F (L) .L. Отсюда следует, что β (L) ⊆L.
прямая сумма в nLab
Прямые суммы и слабые прямые произведения
Контекст
Пределы и пределы
пределы и коллимиты
1-категориальный
-
предел и копредел
-
лимитов и копределов на примере
-
Коммутативность пределов и копределов
-
малый лимит
-
отфильтрованный colimit
-
колимит просеянный
-
подключенный лимит, широкий откат
-
сохраненный лимит, отраженный лимит, созданный лимит
-
продукт, продукт волокна, изменение базы, сопродукт, откат, выталкивание, изменение базы, эквалайзер, коэквалайзер, соединение, встреча, конечный объект, исходный объект, прямой продукт, прямая сумма
-
конечный предел
-
-
Канский добавочный номер
-
взвешенный лимит
-
конец и коэнда
2-категоричный
(∞, 1) -категория
Модельно-категориальная
Идея
Понятие прямой суммы или слабого прямого произведения — это понятие из алгебры, которое действительно имеет смысл в любой категории CC с нулевыми морфизмами (то есть любой категории, обогащенной над замкнутой моноидальной категорией заостренных множеств), поскольку пока существуют необходимые (со) лимиты.
Базовый и знакомый пример — прямая сумма V1⊕V2V_1 oplus V_2 двух векторных пространств V1V_1 и V2V_2 над некоторым полем или, в более общем смысле, двух модулей над некоторым кольцом. Как правило, для II — множество и {Vi} i∈I {V_i } _ {i in I} — индексируемое II семейство векторных пространств или модулей, их прямая сумма ∈i∈IVi bigoplus_ {i in I } V_i — это набор формальных линейных комбинаций элементов в каждом из ViV_i. Это может частично мотивировать терминологию: элемент в прямой сумме — это сумма элементов , по крайней мере, в этих случаях.
Это обобщает двумя разными способами, которые мы называем прямой суммой и слабым прямым произведением . Во многих случаях (как в примере выше) они совпадают, но не всегда. Также во многих случаях прямые суммы будут такими же, как и сопутствующие продукты. В любом случае конечные слабые прямые продукты такие же, как и продукты, но бесконечные версии (почти всегда) разные.
Терминология
Название «слабый прямой продукт» происходит от понятия прямого продукта в алгебре для продукта в конкретной категории, созданного с помощью функтора забывчивости; слабый прямой продукт будет подобъектом прямого продукта (и всего прямого продукта в конечных случаях). Но здесь мы не будем ограничиваться контекстом такой конкретной категории.
Но здесь мы не будем ограничиваться контекстом такой конкретной категории.
Термин «прямая сумма» происходит от конечного побочного продукта (одновременно продукта и сопутствующего продукта) в аддитивных категориях. Аддитивный характер этих побочных продуктов распространяется в бесконечном случае (где побочные продукты обычно больше не появляются) на побочные продукты, а не на продукт. Даже когда прямая сумма не совпадает с побочным продуктом, он все равно сохраняет часть этого аромата.
В классических примерах CC прямая сумма и слабое прямое произведение совпадают.Однако приведенные ниже общие определения различают их в некоторых случаях, и мы используем термины «прямая сумма» и «слабый прямой продукт», чтобы лучше всего вызвать ощущения «как сопутствующий продукт» и «часть продукта».
Определения
Пусть 𝒞 mathcal {C} — категория с произведениями и копроизведениями, а также с нулевыми морфизмами. Пусть II — множество, и пусть (Ai) i∈I (A_i) _ {i in I} — II-индексированное семейство объектов в 𝒞 mathcal {C}, следовательно, функция A: I → Obj ( 𝒞) A: I to Obj ( mathcal {C}).
Теперь мы определим как прямую сумму, так и слабое прямое произведение этого семейства.AiA_i будем называть прямыми слагаемыми или (слабыми) прямыми множителями .
Прямая сумма
Здесь мы должны предположить, кроме того, что 𝒞 mathcal {C} — обычная категория (или иначе имеет хорошее представление об изображении).
Определение
Пусть rr — морфизм копроизведения ∐iAi coprod_i A_i в произведение ∏iAi prod_i A_i, характеризующийся наличием следующих компонентов
(Ai → ∐A → r∏A → Aj) = {IdAiifi = j0ijifi ≠ j,
оставил(
A_i to coprod A stackrel {r} { to} prod A to A_j
верно)
знак равно
оставил{
множество{
Id_ {A_i} & if ; я = j
\
0_ {ij} & если ; я neq j
,}
верно.,
, где 0ij0_ {ij} — нулевой морфизм от AiA_i к AjA_j.
Прямая сумма по семейству {Ai} {A_i } — это изображение
∐iAi → coimr⨁iAI → imriAi
coprod_i A_i overset { coim r} to bigoplus_i A_I overset { im r} to prod_i A_i
морфизма рр.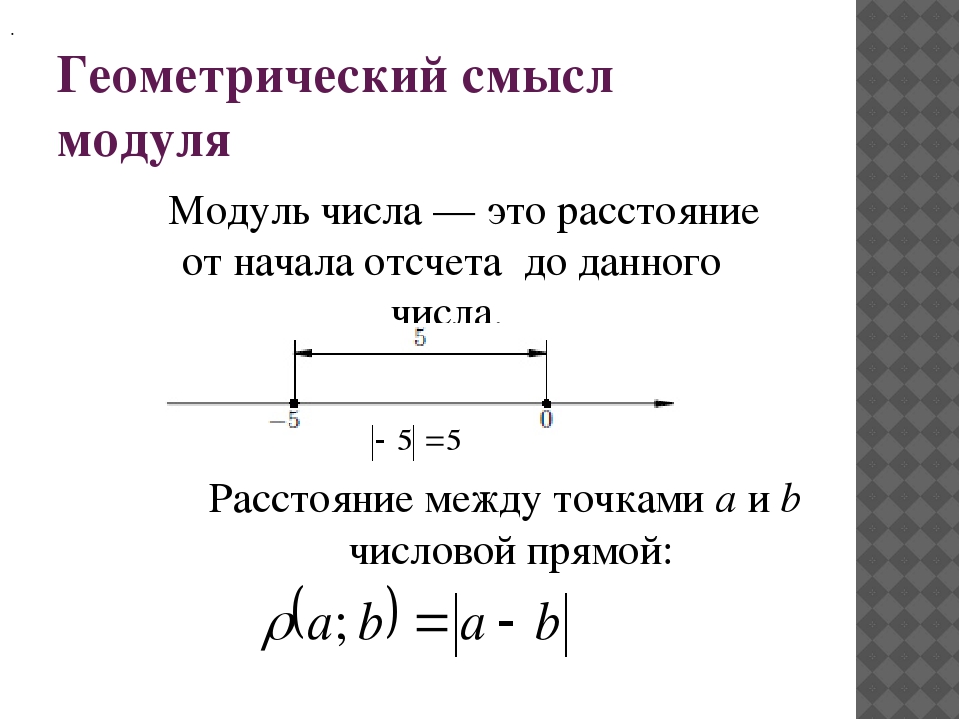
Слабое прямое произведение
Здесь мы рассматриваем финишные изделия
∏i∈FAi prod_ {i in F} A_i
, поскольку FF изменяется на конечных подмножествах индексного множества II. (В конструктивной математике используйте здесь «конечно индексированные» или «конечные по Куратовски» … хотя если II имеет разрешимое равенство, как это имеет место в обычных примерах, то каждое конечно индексированное подмножество II на самом деле конечно в самом строгом смысле.)
Эти конечные произведения образуют прямую систему, индексируемую направленным множеством 𝒫finI mathcal {P} _ {fin} I конечных подмножеств II (упорядоченных по включению) с отображением
∏i∈FAi → ∏i∈GAi, prod_ {i in F} A_i to prod_ {i in G} A_i,
, где F⊆GF substeq G, заданная формулой
∏i∈FAi≅∏i∈FAi × ∏i∈G ∖ F1 → (id, 0) ∏i∈FAi × ∏i∈G ∖ FAi≅∏i∈GAi. prod_ {i in F} A_i cong prod_ {i in F} A_i times prod_ {i in G setminus F} 1 stackrel {(id, 0)} { to} prod_ { i in F} A_i times prod_ {i in G setminus F} A_i cong prod_ {i in G} A_i. wk_i A_i определяется как направленный копредел этой прямой системы.
wk_i A_i определяется как направленный копредел этой прямой системы.
Примеры
Пример
В категориях Grp или Ab (абелевых) групп прямая сумма и слабое прямое произведение согласуются. Для конечного числа объектов это то же самое, что и прямой продукт, который является продуктом в обеих категориях.
Предложение
В этих примерах прямая сумма также может быть описана в более элементарных терминах как подгруппа прямого произведения:
⨁i: IAi = {(ai) i: I | ess∀ (i: I), ai = 0},
bigoplus_ {i: I} A_i =
оставил{
(a_i) _ {i: I} ; | ; ess forall (i: I), ; a_i = 0
верно}
,,
, где «ess∀ess forall» означает «для всех, кроме конечного множества».Это проясняет, что прямая сумма равна прямому продукту, когда задействовано только конечное число объектов.
Для 𝒞 = mathcal {C} = Ab, RRMod это группа формальных линейных комбинаций элементов в слагаемых.
Пример
Для RR кольца прямые суммы в категории RRMod или модулей над RR даются суммами на нижележащих абелевых группах.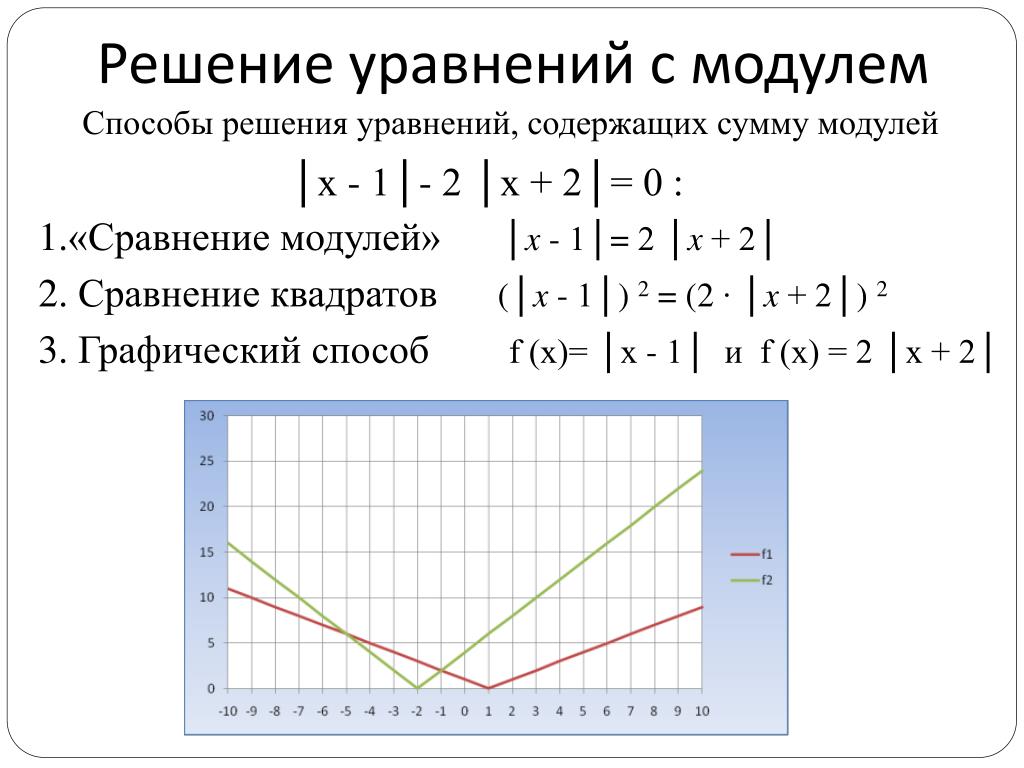
Пример
В категории заостренных множеств прямая сумма и слабое прямое произведение различаются.p прямых сумм для 1≤p≤∞1 leq p leq infty, хотя я не знаю, каким универсальным свойствам они все удовлетворяют.) В этом случае прямая сумма совпадает с копроизведением, а слабое прямое произведение — то же самое, что и произведение даже для бесконечно большого числа объектов. См. Прямую сумму банаховых пространств.
Внутренние прямые суммы
Дан объект BB и семейство подобъектов? AiA_i группы BB (или, в более общем смысле, семейство морфизмов Ai → BA_i to B, или эквивалентно отображение ∐iAi → B coprod_i A_i to B), предположим, что существует прямая сумма ⨁iAi bigoplus_i A_i.Предположим далее, что отображение ∐iAi → B coprod_i A_i в B факторизуется через отображение ∐iAi → ⨁iAi coprod_i A_i в bigoplus_i A_i (что означает, что оно уникально множится, если ∐iAi → ⨁iAi coprod_i A_i to bigoplus_i A_i эпично, так как должно быть в обычной категории). Наконец, предположим, что (или) фактор-отображение ⨁iAi → B bigoplus_i A_i to B является изическим. Затем мы говорим, что BB — это внутренняя прямая сумма AiA_i.
Наконец, предположим, что (или) фактор-отображение ⨁iAi → B bigoplus_i A_i to B является изическим. Затем мы говорим, что BB — это внутренняя прямая сумма AiA_i.
Напротив, абстрактно определенная прямая сумма ⨁iAi bigoplus_i A_i может называться внешней прямой суммой .Эти термины обычно используются с конкретными категориями, где AiA_i может быть задан независимо (для внешней прямой суммы) или как подмножество некоторого окружающего пространства (либо BB, либо что-то из того, что BB является подмножеством) для внутренней прямой суммы. В слишком абстрактном контексте разницы нет: с одной стороны, любая внутренняя прямая сумма тем более изоморфна любой внешней прямой сумме; с другой стороны, для внешней прямой суммы существует естественное отображение ∐iAi → ⨁iAi coprod_i A_i to bigoplus_i A_i, относительно которого внешняя прямая сумма является внутренней прямой суммой.3 | y in mathbb {F} } ), то уравнение (4.4.2) остается в силе.
Если (U = U_1 + U_2 ), то для любого (u in U ) существуют (u_1 in U_1 ) и (u_2 in U_2 ) такие, что (u = u_1 + u_2. )
Если так получилось, что (u ) можно однозначно записать как (u_1 + u_2 ), то (U ) называется прямой суммой (U_1 ) и (U_2. )
Определение 4.4.3: Прямая сумма
Предположим, что каждое (u in U ) может быть однозначно записано как (u = u_1 + u_2 ) для (u_1 in U_1 ) и (u_2 in U_2 ).{2m + 1} }. ]
Тогда ( mathbb {F} [z] = U_1 oplus U_2. )
Предложение 4.4.6 . Пусть (U_1, U_2 subset V ) — подпространства. Тогда (V = U_1 oplus U_2 ) тогда и только тогда, когда выполняются следующие два условия:
- (V = U_1 + U_2; )
- Если (0 = u_1 + u_2 ) с (u_1 in U_1 ) и (u_2 in U_2 ), тогда (u_1 = u_2 = 0. )
Доказательство.
((« Rightarrow») ) Предположим, (V = U_1 oplus U_2 ).Тогда по определению выполняется условие 1. Конечно, (0 = 0 + 0 ), и, поскольку по уникальности это единственный способ записать (0 in V ), мы имеем (u_1 = u_2 = 0 ).
((« Leftarrow») ) Предположим, что выполнены условия 1 и 2. По условию 1 для всех (v in V ) существуют (u_1 in U_1 ) и (u_2 in U_2 ) такие, что (v = u_1 + u_2 ). Предположим, (v = w_1 + w_2 ) с (w_1 in U_1 ) и (w_2 in U_2 ). Вычитая два уравнения, получаем
[0 = (u_1 — w_1) + (u_2 — w_2), ]
, где (u_1 — w_1 in U_1 ) и (u_2 — w_2 in U_2 ).По условию 2 это подразумевает (u_1 — w_1 = 0 ) и (u_2 — w_2 = 0 ), или, что эквивалентно, (u_1 = w_1 ) и (u_2 = w_2 ), как требуется.
Предложение 4.4.7. Пусть (U_1, U_2 subset V ) будут подпространствами. Тогда (V = U_1 oplus U_2 ) тогда и только тогда, когда выполняются следующие два условия:
- (V = U_1 + U_2; )
- (U_1 cap U_2 = {0 }.
 )
)
Доказательство.
((« Rightarrow») ) Предположим, (V = U_1 oplus U_2 ).Тогда по определению выполняется условие 1. Если (u in U_1 cap U_2 ), то (0 = u + (−u) ) с (u in U_1 ) и (- u in U_2 ) (почему?). По предложению 4.4.6 имеем (u = 0 ) и (- u = 0 ), так что (U_1 cap U_2 = {0 }. )
((« Leftarrow») ) Предположим, что выполнены условия 1 и 2. Чтобы доказать, что выполняется (V = U_1 oplus U_2 ), предположим, что
[0 = u_1 + u_2, rm {~ где ~} u_1 в U_1 rm {~ и ~} u_2 в U_2. tag {4.3} ]
По предложению 4.4.6 достаточно показать, что (u_1 = u_2 = 0 ).3 neq U_1 oplus U_2 oplus U_3 ), поскольку, например,
[(0, 0, 0) = (0, 1, 0) + (0, 0, 1) + (0, -1, -1). ]
Но (U_1 cap U_2 = U_1 cap U_3 = U_2 cap U_3 = {0 } ), так что аналог предложения 4.4.7 не выполняется.
Авторы
Версии этого учебника в твердом и мягком переплете доступны на сайте WorldScientific. com.
com.
О. В. Камловский, “Сумма модулей коэффициентов Уолша для некоторых сбалансированных булевых функций”, Матем.Вопр. Криптогр., 8: 4 (2017), 75–98
|
|
Эта статья цитируется в научной статье 1 (всего в статье 1 ) Сумма модулей коэффициентов Уолша для некоторых сбалансированных булевых функций О.В. Камловский ООО «Центр Сертификационных Исследований», Москва Аннотация: Ключевые слова: DOI: Полный текст: Библиографические базы данных: УДК: Образец цитирования: Цитирование в формате AMSBIB Варианты соединения: Цитирующие статьи в Google Scholar: Эта публикация цитируется в следующих статьях:
|
прямой перевод% 20sum% 20of% 20modules — английский французский перевод прямого% 20sum% 20of% 20modulesВаш поиск не дал результатов
|
Модуль числа — теория и решение задач
Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂
![]()
А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.
Вот смотри…
Ситуация первая
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?
Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.
Ситуация третья
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее…
Модуль числа — коротко о главном
Определение модуля:
Модуль (абсолютная величина) числа ( displaystyle x) — это само число ( displaystyle x), если ( displaystyle xge 0), и число ( displaystyle -x), если ( displaystyle x<0):
( displaystyle left| x right|=left{ begin{array}{l}x, xge 0\-x, x<0end{array} right.)
Свойства модуля:
- Модуль числа есть число неотрицательное: ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0);
- Модули противоположных чисел равны: ( left| -x right|=left| x right|);
- Модуль произведения двух (и более) чисел равен произведению их модулей: ( left| xcdot yright|=left| x right|cdot left|yright|);
- Модуль частного двух чисел равен частному их модулей: ( displaystyle left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0});
- Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:( left| x+y right|le left| x right|+left| y right|);
- Постоянный положительный множитель можно выносить за знак модуля: ( left| cx right|=ccdot left| x right|) при ( displaystyle c>0);
- Квадрат модуля числа равен квадрату этого числа: ( {{left| x right|}^{2}}={{x}^{2}}).
Кстати, в продолжение этой темы у нас есть отличная статья: «Уравнения с модулем«. Когда прочитаешь эту статью, обязательно ознакомься и со второй.
И просто чтобы ты знал, модуль часто попадается при решении квадратных уравнений или иррациональных.
Что же такое модуль числа?
Представь, что это ты.
![]()
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления ( 0).
![]()
Итак, ты делаешь ( 3) шага вперёд и оказываешься в точке с координатой ( 3).
![]()
Это означает, что ты удалился от места, где стоял на (3) шага (( 3) единичных отрезка).
То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно ( 3).
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой ( 0) сделать ( 3) шага в обратную сторону, то окажешься в точке с координатой ( -3).
![]()
Какое расстояние было пройдено в первом и во втором случае?
Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки (( 3) и ( -3)), в которых ты оказался одинаково удалены от точки, из которой было начато движение (( 0)).
![]()
Таким образом, мы приблизились к понятию модуля.
Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа ( 5) будет ( 5). Модуль числа ( -5) также равен ( 5).
Потому что расстояние не может быть отрицательным! Модуль – это абсолютная величина.
Обозначается модуль просто:
( |mathbf{a}|,) (( a) — любое число).
Итак, найдём модуль числа ( 3) и ( -3):
( left| mathbf{3} right|=mathbf{3})
( left| -mathbf{3} right|=mathbf{3}.)
Основные свойства модуля
Первое свойство модуля
Модуль не может быть выражен отрицательным числом ( |mathbf{a}|text{ }ge text{ }mathbf{0})
То есть, если ( mathbf{a}) – число положительное, то его модуль будет равен этому же числу.
Если ( mathbf{a}text{ }>text{ }mathbf{0},) то ( displaystyle left| a right|=a).
Если ( a) – отрицательное число, то его модуль равен противоположному числу.
Если ( atext{ }<text{ }mathbf{0},) то ( |mathbf{a}|text{ }=text{ }-mathbf{a})
А если ( a=0)? Ну, конечно! Его модуль также равен ( 0):
Если ( a=0), то ( |mathbf{a}|=mathbf{a}), или ( displaystyle left| 0 right|=0).
Из этого следует, что модули противоположных чисел равны, то есть:
( left| -4 right|text{ }=text{ }left| 4 right|text{ }=text{ }4;)
( left| -7 right|text{ }=text{ }left| 7 right|text{ }=text{ }7.)
А теперь потренируйся:
- ( left| 9 right|text{ }=text{ }?;)
- ( left| -3 right|text{ }=text{ }?;)
- ( left| 16 right|text{ }=text{ }?;)
- ( left| 8 right|text{ }=text{ }?;)
- ( left| -17 right|text{ }=text{ }?.)
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда? А если перед тобой вот такое число: ( left| 2-sqrt{5} right|=?)
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль:
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим ( 2-sqrt{5}):
( 2<sqrt{5}) (Забыл, что такое корень? Бегом повторять!)
Если ( 2<sqrt{5}), то какой знак имеет ( 2-sqrt{5})? Ну конечно, ( 2-sqrt{5}<0)!
А, значит, знак модуля раскрываем, меняя знак у выражения:
( left| 2-sqrt{5} right|=-left( 2-sqrt{5} right)=-2+sqrt{5}=sqrt{5}-2)
Разобрался? Тогда попробуй сам:
- ( left| sqrt{3}-1 right|=?)
- ( left| 3-sqrt{7} right|=?)
- ( left| 2-sqrt{7} right|=?)
- ( left| sqrt{13}-4 right|=?)
Ответы:
( sqrt{3}-1; 3-sqrt{7}; sqrt{7}-2; 4-sqrt{13.})
Какими же ещё свойствами обладает модуль?
Во-первых, если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.
То есть: ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|)
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
Например:
( left| mathbf{5}cdot mathbf{7} right|text{ }=text{ }left| mathbf{5} right|cdot left| mathbf{7} right|text{ }=text{ }mathbf{5}cdot mathbf{7}text{ }=text{ }mathbf{35};)
( left| mathbf{3}cdot left( -mathbf{2} right) right|text{ }=text{ }left| mathbf{3} right|cdot left| -mathbf{2} right|text{ }=text{ }mathbf{3}cdot mathbf{2}text{ }=text{ }mathbf{6}.)
А что, если нам нужно разделить два числа (выражения) под знаком модуля? Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
( displaystyle |frac{a}{b}|=frac{|a|}{|b|}) при условии, что ( mathbf{b}ne mathbf{0}) (так как на ноль делить нельзя).
Еще одно свойство модуля…
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел.
( |a+bleft| text{ }le text{ } right|aleft| + right|b|)
Почему так? Всё очень просто! Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное.
Допустим, что числа ( a) и ( b) оба положительные. Тогда левое выражение будет равно правому выражению. Рассмотрим на примере:
| ( left| mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{10} right|text{ }=text{ }mathbf{10}) | ( left| mathbf{3} right|+left| mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Выражения также равны, если оба числа отрицательны:
| ( displaystyle |-3+(-7)|~=~|-3-7|~)( displaystyle=|-10|=10) | ( |-mathbf{3}left| + right|-mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
| ( left| -mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{4} right|text{ }=text{ }mathbf{4}) | ( |-mathbf{3}left| + right|mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
или
| ( left| mathbf{3}+left( -mathbf{7} right) right|text{ }=text{ }left| -mathbf{4} right|text{ }=text{ }mathbf{4}) | ( left| mathbf{3} right|+left| -mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
( mathbf{4}<mathbf{10})
Рассмотрим еще парочку полезных свойств модуля
Что если перед нами такое выражение:
( left| 7x right|)
Что мы можем сделать с этим выражением?
Значение x нам неизвестно, но зато мы уже знаем, что ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|), а значит ( left| 7x right|=left| 7 right|cdot left| x right|). Число ( 7) больше нуля, а значит можно просто записать:
( left| 7x right|=left| 7 right|cdot left| x right|=7left| x right|)
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
( left| cx right|=ccdot left| x right|,) при ( c>0)
А чему равно такое выражение:
( {{left| x right|}^{2}}=?)
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?
Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства.
И что же получается? А вот что:
( {{left| x right|}^{2}}={{x}^{2}})
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
( {{left| 5 right|}^{2}}={{5}^{2}}=25)
( {{left| -5 right|}^{2}}=?)
Ну, и почему сомнения? Действуем смело!
( {{left| -5 right|}^{2}}={{5}^{2}}=25)
Во всем разобрался? Тогда вперед тренироваться на примерах!
Тренировка на примерах
1. Найдите значение выражения ( |xleft| text{ }+text{ } right|y|), если ( x=text{ }-7,5text{ },y=text{ }12.)
2. У каких чисел модуль равен ( 5)?
3. Найдите значение выражений:
а) ( |3|text{ }+text{ }|-9|;)
б) ( |-5|text{ }-text{ }|6|;)
в) ( |15left| cdot right|-3|;)
г) ( displaystyle frac{|8|}{|-2|}).
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Решение 1:
Итак, подставим значения ( x) и ( y) в выражение ( |mathbf{x}left| text{ }-text{ } right|mathbf{y}|.) Получим:
( |-7,5|text{ }+text{ }|12|text{ }=7,5text{ }+text{ }12text{ }=text{ }19,5.)
Решение 2:
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное ( 5) имеют два числа: ( 5) и ( -5).
Решение 3:
а) ( |3|text{ }+text{ }|-9|=text{ }3+9=text{ }12;)
б) ( |-5|-text{ }left| 6 right|text{ }=text{ }5-6=text{ }-1;)
в) ( |15left| cdot right|-3|text{ }=text{ }15cdot 3=text{ }45;)
г) ( frac{|8|}{|-2|}=frac{8}{2}=4.)
Все уловил? Тогда пора перейти к более сложному!
Решение более сложных примеров
Попробуем упростить выражение ( left| sqrt{3}-2 right|+left| sqrt{3}+5 right|)
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
( displaystyle sqrt{3} approx 1,7). Получается, значение первого выражения под модулем ( displaystyle sqrt{3}-2approx 1,7-2approx -0,3text{ }).
( -0,3<0), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
![]()
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Модуль числа и его свойства (строгие определения и доказательства)
Модуль (абсолютная величина) числа ( x) — это само число ( x), если ( xge 0), и число ( -x), если ( x<0):
( left| x right|=left{ begin{array}{l}x,text{ }xge 0\-x,text{ }x<0end{array} right.)
Например: ( left| 4 right|=4;text{ }left| 0 right|=0;text{ }left| -3 right|=-left( -3 right)=3.)
Пример:
Упростите выражение ( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|).
Решение:
( sqrt{5}-3<0Rightarrow left| sqrt{5}-3 right|=-left( sqrt{5}-3 right)=3-sqrt{5};)
( sqrt{5}+1>0Rightarrow left| sqrt{5}+1 right|=sqrt{5}+1;)
( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|=3-sqrt{5}+sqrt{5}+1=4.)
Основные свойства модуля (итог)
Для всех ( x,yin mathbb{R}):
- ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0;)
- ( left| -x right|=left| x right|;)
- ( left| xcdot y right|=left| x right|cdot left| y right|;)
- ( left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0};)
- ( left| x+y right|le left| x right|+left| y right|)
- ( left| cx right|=ccdot left| x right|, при text{ }c>0)
- ( {{left| x right|}^{2}}={{x}^{2}})
Докажите свойство модуля: ( left| x+y right|le left| x right|+left| y right|)
Доказательство:
Предположим, что существуют такие ( x;yin mathbb{R}), что ( left| x+y right|>left| x right|+left| y right|.) Возведем левую и правую части неравенства в квадрат (это можно сделать, т.к. обе части неравенства всегда неотрицательны):
( displaystyle begin{array}{l}left| x+y right|>left| x right|+left| y right|Leftrightarrow \{{left( x+y right)}^{2}}>{{left( left| x right|+left| y right| right)}^{2}}Leftrightarrow \{{x}^{2}}+2xy+{{y}^{2}}>{{x}^{2}}+2cdot left| x right|cdot left| y right|+{{y}^{2}}Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end{array})
а это противоречит определению модуля.
Следовательно, таких ( x;yin mathbb{R}) не существует, а значит, при всех ( x,text{ }yin mathbb{R}) выполняется неравенство ( left| x+y right|le left| x right|+left| y right|.)
А теперь самостоятельно…
Докажите свойство модуля: ( left| cx right|=ccdot left| x right|, при text{ }c>0)
Воспользуемся свойством №3: ( left| ccdot x right|=left| c right|cdot left| x right|), а поскольку ( c>0text{ }Rightarrow text{ }left| c right|=c), тогда
( left| cx right|=ccdot left| x right|), ч.т.д.
Упростите выражение ( left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|)
Чтобы упростить, нужно раскрыть модули. А чтобы раскрыть модули, нужно узнать, положительны или отрицательны выражения под модулем:
Подготовка к ЕГЭ на 90+ в мини-группах
![]()
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
-
Задание 1
Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100.
а) Может ли частное этого числа и суммы его цифр быть равным 90?
б) Может ли частное этого числа и суммы его цифр быть равным 88?
в) Какое наибольшее натуральное значение может иметь частное данного числа и суммы его цифр?
Разбор задания
СвернутьПусть данное число равно 100 a + 10 b + c где a,b и c — цифры сотен, десятков и единиц соответственно. Если частное этого числа и суммы его цифр равно k, то выполнено

а) Если частное равно 90, то
 Преобразуем:
Преобразуем:  что верно, например, при
что верно, например, при  (получено подбором в предположении, что c=0, так как это убирает “неудобное” число 89). Действительно, частное числа 810 и суммы его цифр (10) равно 90.
(получено подбором в предположении, что c=0, так как это убирает “неудобное” число 89). Действительно, частное числа 810 и суммы его цифр (10) равно 90.б) Если частное равно 88, то
 Если рассуждать в натуральных числах, то ясно, что b и c должны быть очень маленькими (иначе их сумма не будет равна 12 a). Краткий перебор показывает, что это невозможно. Формализуем рассуждения:
Если рассуждать в натуральных числах, то ясно, что b и c должны быть очень маленькими (иначе их сумма не будет равна 12 a). Краткий перебор показывает, что это невозможно. Формализуем рассуждения:  Значит,
Значит,  или
или  Но ни 78, ни 87 не делится на 12. Значит, частное трёхзначного числа и суммы его цифр не может быть равным 88.
Но ни 78, ни 87 не делится на 12. Значит, частное трёхзначного числа и суммы его цифр не может быть равным 88.в) Пусть k — наибольшее натуральное значение частного числа, не кратного 100, и суммы его цифр. Тогда

Учитывая, что b+c>0, получаем:

откуда

Частное числа 910 и суммы его цифр равно 91. Значит, наибольшее натуральное значение частного трёхзначного числа, не кратного 100, и суммы его цифр равно 91.
Ответ: а) да; б) нет; в) 91.
-
Задание 2
Длины сторон прямоугольника ― натуральные числа, а его периметр равен 4000. Известно, что длина одной стороны прямоугольника равна
 от длины другой стороны, где n ― также натуральное число.
от длины другой стороны, где n ― также натуральное число.а) Какое наибольшее значение может принимать площадь прямоугольника?
б) Какое наименьшее значение может принимать площадь прямоугольника?
в) Найдите все возможные значения, которые может принимать площадь прямоугольника, если дополнительно известно, что n <100.
Разбор задания
Свернутьа) Так как периметр равен 4000, то сумма смежных сторон прямоугольника равна 2000. Известно, что наибольшее значение площади прямоугольника при фиксированном периметре достигается в том случае, если он является квадратом. Таким образом, его стороны должны быть равны 1000, что не противоречит условию (длины обеих сторон натуральные числа, длина одной стороны равна 100% от длины другой). Значит, наибольшее значение площади прямоугольника равно 1 000 000.
б) Пусть меньшая сторона прямоугольника равна x
 тогда другая сторона равна
тогда другая сторона равна  В этом случае площадь прямоугольника равна
В этом случае площадь прямоугольника равна  Графиком данной функции является парабола, ветви которой направлены вниз, а число x не превосходит абсциссы вершины параболы (абсцисса вершины этой параболы равна 1000). Следовательно, значение функции будет тем меньше, чем дальше находится число x от абсциссы вершины. Таким образом, наименьшее значение функции достигается при x=1, а тогда площадь равна 1999. В этом случае условие также соблюдается, так как число 1999 равно 199900% от числа 1.
Графиком данной функции является парабола, ветви которой направлены вниз, а число x не превосходит абсциссы вершины параболы (абсцисса вершины этой параболы равна 1000). Следовательно, значение функции будет тем меньше, чем дальше находится число x от абсциссы вершины. Таким образом, наименьшее значение функции достигается при x=1, а тогда площадь равна 1999. В этом случае условие также соблюдается, так как число 1999 равно 199900% от числа 1.в) Пусть a ― это сторона,
 от которой равны другой стороне. Тогда другая сторона равна
от которой равны другой стороне. Тогда другая сторона равна  Поскольку сумма смежных сторон прямоугольника равна 2000, получаем:
Поскольку сумма смежных сторон прямоугольника равна 2000, получаем:
Так как a и n ― целые числа, то число 200 000 кратно числу 100+n.
Заметим, что
 так как n<100. Следовательно, требуется найти все делители числа 200 000, меньшие 200, но большие 100. Так как
так как n<100. Следовательно, требуется найти все делители числа 200 000, меньшие 200, но большие 100. Так как  то искомый делитель может содержать в своем разложении на простые множители лишь 2 и 5, причем соответствующие степени не превосходят 6 и 5.
то искомый делитель может содержать в своем разложении на простые множители лишь 2 и 5, причем соответствующие степени не превосходят 6 и 5.Для поиска переберём степени пятёрки, домножая их на степени двойки:
1)
 ; очевидно, что
; очевидно, что  ; не подходит.
; не подходит.2)
 – мало,
– мало,  – годится,
– годится,  – много.
– много. 3)
 – мало,
– мало,  – много.
– много.4)
 – годится;
– годится;  – много.
– много. 5)
 – много.
– много. Итого получилось 2 варианта. Первый:
 площадь равна 937500. Второй:
площадь равна 937500. Второй:  площадь равна 640 000.
площадь равна 640 000.Ответ: а) 1 000 000; б) 1999; в) 937 500 или 640 000.
-
Задание 3
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно −3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно −8.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Разбор задания
СвернутьПусть среди написанных чисел k положительных, l отрицательных и m нулей (крайне важно не забыть, что ноль не является ни отрицательным, ни положительным числом!). Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому
 .
.а) Заметим, что в левой части приведённого выше равенства каждое слагаемое делится на 4, поэтому k + l + m — количество целых чисел — делится на 4. По условию
 , поэтому k + l + m = 44. Таким образом, написано 44 числа.
, поэтому k + l + m = 44. Таким образом, написано 44 числа.б) Приведём равенство
 к виду
к виду  . Так как
. Так как  , получаем, что
, получаем, что  , откуда
, откуда  (равенство для целых неотрицательных чисел в этом неравенстве может быть достигнуто только при m=l=k=0, что невозможно). Следовательно, отрицательных чисел больше, чем положительных.
(равенство для целых неотрицательных чисел в этом неравенстве может быть достигнуто только при m=l=k=0, что невозможно). Следовательно, отрицательных чисел больше, чем положительных.в) Оценка: Подставим k + l + m = 44 в правую часть равенства 4k − 8l = −3(k + l + m), откуда k = 2l − 33 . Так как
 , получаем:
, получаем: 
 , то есть положительных чисел не более 17.
, то есть положительных чисел не более 17.Мы доказали, что чисел не может быть более 17; но достигается ли 17? Пример строится тривиально: возьмём 17 положительных чисел, равных среднему арифметическому положительных чисел (то есть 4), и подгоним нужное количество отрицательных чисел, равных -8, и нулей так, чтобы среднее арифметическое всего ряда равнялось -3. С помощью перебора находим, что можно взять 25 раз число -8 и два раза число 0. Тогда
 указанный набор удовлетворяет всем условиям задачи.
указанный набор удовлетворяет всем условиям задачи.Ответ: а) 44; б) отрицательных; в) 17.
-
Задание 4
а) Можно ли число 2014 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?
б) Можно ли число 199 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?
в) Найдите наименьшее натуральное число, которое можно представить в виде суммы пяти различных натуральных чисел с одинаковой суммой цифр.
Разбор задания
Свернутьа) Заметим, что сумма цифр исходного числа является однозначным числом; это подсказывает, что сумму можно попробовать поискать как сумму однозначного и четырёхзачного. Перебирая, начиная от 2014 = 2013 + 1 и повышая второе слагаемое на 1, отнимая от первого по 1, получаем один из возможных ответов: 2014 = 2006 + 8.
б) 199 можно представить либо как сумму однозначного и трёхзначного, либо как сумму двухзначного и трёхзначного. Заметим, что в первом случае сумма цифр обоих чисел равняется 19 (проверяется перебором); во втором же случае имеем:
 где a, b, c, d – цифры. Заметим, что b + d = 9, а также, в силу того, что в десятки при сложении ничего переноситься не может (в таком случае максимально возможная цифра единиц может получиться при сложении 9+9 = 18 – не подходит), следовательно, также имеем a + c = 9. Таким образом, сумма цифр обеих чисел равна 1 + a + b + c + d = 1 + 9 + 9 = 19.
где a, b, c, d – цифры. Заметим, что b + d = 9, а также, в силу того, что в десятки при сложении ничего переноситься не может (в таком случае максимально возможная цифра единиц может получиться при сложении 9+9 = 18 – не подходит), следовательно, также имеем a + c = 9. Таким образом, сумма цифр обеих чисел равна 1 + a + b + c + d = 1 + 9 + 9 = 19.Мы получили, что в любом случае сумма цифр обоих чисел должна равняться 19. От нас требуется, что сумма цифр каждого из двух чисел равнялась друг другу, но 19 – число нечётное, поэтому такое невозможно.
в) Ясно, что чем меньшую сумму цифр мы возьмём, тем лучше. Проверим суммы, подбирая наименьшые числа:
1 + 10 + 100 + 1000 + 100000 = 11111 (обратите внимание: из-за использования нуля, то есть дополнительного разряда, сумма очень сильно растёт; надо этого избегать)
2 + 11 + 20 + 110 + 200 = 343;
3 + 12 + 21 + 30 + 120 = 186;
4 + 13 + 22 + 31 + 40 = 120
5 + 14 + 23 + 32 + 41 = 125
В дальнейшем каждая следующая сумма будет как минимум на 5 больше, так как каждое соответствующее число будет, по меньшей мере, на 1 больше предыдущего. Поэтому 120 является ответом.
Ответ: а) да; б) нет; в) 110.
-
Задание 5
Каждое из чисел
 умножают на каждое из чисел
умножают на каждое из чисел  и перед каждым из полученных произведений произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
и перед каждым из полученных произведений произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?Разбор задания
СвернутьОтметим, что задача эквивалентна поиску максимального и минимального по модулю значения выражения вида:

Нам надо расставить знаки плюс или минус. Для максимально возможного значения выражения, очевидно, надо взять плюс; Вычисление можно произвести вручную или воспользоваться формулой суммы арифметической прогрессии:

Оценка минимального значения: так как сумма оказалась нечетной, то число нечетных слагаемых в ней нечетно, причем это свойство всей суммы не меняется при смене знака любого ее слагаемого. Поэтому любая из получающихся сумм будет нечетной, а значит, не будет равна 0. Следовательно, минимальное по модулю значение больше или равно 1.
Как достигнуть значения выражения, равного 1? Ясно, что для этого в изначальном произведении оба выражения должны равняться 1. Подбором расставим знаки в скобках нужым образом:

Ответ: 1 и 4131.
Ответ: 1 и 4131.
-
Задание 6
На доске написано число 7. Раз в минуту Вася дописывает на доску одно число: либо вдвое большее какого-то из чисел на доске, либо равное сумме каких-то двух чисел, написанных на доске (таким образом, через одну минуту на доске появится второе число, через две ― третье и т.д.).
а) Может ли в какой-то момент на доске оказаться число 2012?
б) Может ли в какой-то момент сумма всех чисел на доске равняться 63?
в) Через какое наименьшее время на доске может появиться число 784?
Разбор задания
Свернутьа) Заметим, что каждое число на доске будет делиться на 7. Действительно, исходное число делится на 7, в случае удвоения числа делящегося на 7, получится число, делящееся на 7. А при сложении чисел, делящихся на 7, также получится число, делящееся на 7. Таким образом, все числа на доске будут делиться на 7, а 2012 на 7 не делится, следовательно, оно не может появиться на доске.
б) Да, может. Пример: 7, 14 (удвоенное число 7), 14 (удвоенное число 7), 14 (удвоенное число 7), 14 (удвоенное число 7). Сумма полученных 5 чисел равна 63.
в) Как было замечено в пункте а), все числа на доске будут делиться на 7. Рассмотрим аналогичную задачу, разделив исходное число 7 и то число, которое нужно получить, то есть 784, на 7. От этого количество операций не изменится. Таким образом, достаточно за наименьшее количество операций получить число 112, начав с числа 1.
Заметим, что наибольшее число, которое может получиться на доске через 6 минут, равно 64 (если Вася каждый раз будет удваивать текущее наибольшее число). Следовательно, если в первые 6 минут Вася каждый раз удваивал наибольшее число на доске, то число 112 нельзя получить за 7 минут: если число 64 удвоить, то получится 128, а если прибавить к нему число, не превосходящее 32, то 112 не получится.
В том случае, если в течение первых 6 минут Вася использовал хотя бы одно сложение вместо удвоения, то при первом использовании сложения наибольшее число, записанное на доске увеличилось не более, чем в полтора раза: действительно, в этом случае самый большой результат получится тогда, когда мы к максимальному на данный момент числу прибавим второе по величине, то есть, его половину (напомним, что мы рассматриваем первый случай сложения, то есть до этого были только удвоения). Таким образом, даже если в течение первых 7 минут сделано 6 удвоений и одно сложение (в некотором порядке), то наибольшее число, которое может получиться, равно 96, что меньше 112.
Итак, за 7 минут число 112 получить невозможно.
Приведем пример, как его получить за 8 минут:



Ответ: а) нет; б) да; в) 8.
-
Задание 7
Имеется 8 карточек. На них записывают по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Какое наименьшее целое неотрицательное число может в результате получиться?
Разбор задания
Свернутьа) Среди восьми данных чисел нет противоположных. Значит, сумма чисел на каждой карточке не равна 0. Поэтому всё произведение не может равняться нулю.
б) Среди восьми данных чисел пять нечётных. Значит, на какой-то карточке попадётся два нечётных числа, и их сумма чётная. Поэтому всё произведение чётно и не может равняться 1.
в) Среди восьми данных чисел пять нечётных. Значит, хотя бы на двух карточках с обеих сторон написаны нечётные числа, и сумма чисел на каждой из этих карточек чётная. Поэтому всё произведение делится на 4.
Наименьшее целое положительное число, делящееся на 4, это 4. Оно получается при следующем наборе пар чисел на карточках: (1; -2); (-2; 1); (-3; 4); (4; -3); (-5; 7); (7; -5); (-8; 9); (9; -8).
Ответ: а) нет; б) нет; в) 4.
-
Задание 8
Целое число S является суммой не менее трех последовательных членов непостоянной арифметической прогрессии, состоящей из целых чисел.
а) Может ли S равняться 8?
б) Может ли S равняться 1?
в) Найдите все значения, которые может принимать S.
Разбор задания
Свернутьа) Число 8 является суммой четырех последовательных членов арифметической прогрессии. Например, 8 = − 1 + 1 + 3 + 5.
б) Пусть число 1 является суммой первых k членов арифметической прогрессии с первым членом а и разностью d. Тогда

Значит, число k — делитель 2, что противоречит условию

в) Любое натуральное число
 является суммой арифметической прогрессии
является суммой арифметической прогрессии  состоящей из
состоящей из  членов. Если заменить все члены этой прогрессии на противоположные, то получится арифметическая прогрессия, состоящая из 2n членов, сумма которой равна −n.
членов. Если заменить все члены этой прогрессии на противоположные, то получится арифметическая прогрессия, состоящая из 2n членов, сумма которой равна −n.В предыдущем пункте мы показали, что S не может равняться 1. Аналогично можно показать, что S не может равняться −1 (например, так: если бы мы могли получить в сумме -1, то, заменив знаки всех чисел на противоположные, мы могли бы получить 1). Число S может равняться 0, например, для прогрессии −1; 0; 1. Таким образом, S может принимать любые целые значения, кроме −1 и 1.
Ответ: а) да; б) нет; в) любые целые значения, кроме -1 и 1.
-
Задание 9
Коля множил некоторое натуральное число на соседнее натуральное число, и получил произведение, равное m. Вова умножил некоторое четное натуральное число на соседнее четное натуральное число и получил произведение, равное n.
а) Может ли модуль разности чисел m и n равняться 6?
б) Может ли модуль разности чисел m и n равняться 13?
в) Какие значения может принимать модуль разности чисел m и n?
Разбор задания
Свернутьа) Да, например, Коля умножил 6 на 7, получив 42, а Вова умножил 6 на 8, получив 48. Модуль разности полученных произведений равен 6.
б) Заметим, что произведение последовательных чисел всегда четно, так как одно из них четно. Таким образом, Колино произведение будет четным. Вовино же произведение четно в силу того, что он перемножает два четных числа. Значит, и модуль разности чисел a и b будет четным, таким образом, он не может быть равен 13.
в) Как было показано в пункте б) модуль разности будет четным. Покажем, что он не может быть равен нулю. Пусть Коля перемножал числа x и x+1, а Вова ― числа y и y+2. Тогда, если модуль разности их произведений равен нулю, имеем:

Заметим, что x С другой стороны,
 так как
так как 
Итак,
 но натуральное число не может лежать между двумя соседними натуральными числами. Значит, модуль разности не может равняться 0. Тогда он не меньше 2, так как четен.
но натуральное число не может лежать между двумя соседними натуральными числами. Значит, модуль разности не может равняться 0. Тогда он не меньше 2, так как четен.Покажем, что он может принимать любое четное натуральное значение. Пусть Коля умножил четное число n на n+1, а Вова умножил n на n+2 Тогда модуль разности их произведений равен:

ввиду того, что n ― любое четное натуральное число, то искомый модуль разности может принимать любое четное натуральное значение.
Ответ: а) да; б) нет; в) все чётные натуральные числа.
-
Задание 10
В игре «Дротики» есть 20 наружных секторов, пронумерованных от 1 до 20 и два центральных сектора. При попадании в наружный сектор игрок получает количество очков, совпадающее с номером сектора, а за попадание в центральные сектора он получает 25 или 50 очков соответственно. В каждом из наружных секторов есть области удвоения и утроения, которые, соответственно, удваивают или утраивают номинал сектора. Так, например, попадание в сектор 10 (не в зоны удвоения и утроения) дает 10 очков, в зону удвоения сектора ― 20 очков, в зону утроения ― 30 очков.
а) Может ли игрок тремя бросками набрать ровно 167 очков?
б) Может ли игрок шестью бросками набрать ровно 356 очков?
в) С помощью какого наименьшего количества бросков, игрок может набрать ровно 1001 очко?
Разбор задания
Свернутьа) Да, например, при попадании в утроение сектора 20, утроение сектора 19 и центральный сектор 50 получаем: 60 + 57 + 50 = 167.
б) Наибольшее количество очков, которое может набрать игрок одним броском ― 60 (утроение 20), далее идут: 57 очков (утроение 19) и 54 очка (утроение 18). Попадание во все остальные сектора и зоны дает меньше 54 очков. Если все шесть бросков были по 60 очков, то игрок набрал 360 очков, что больше 356. Если хотя бы один бросок на 60 очков заменить броском на 54 очка или меньше, то сумма уменьшится как минимум на 6, а, значит, станет не больше 354 очков, что меньше 356 очков. Следовательно, бросок на 60 очков можно заменять только броском на 57 очков. Но одна такая замена дает итоговый результат 357 очков, а хотя бы две замены ― не более 354 очков. Значит, 356 очков шестью бросками набрать невозможно.
в) Как было показано в пункте б) каждый бросок приносит игроку не более 60 очков. Значит, за 16 бросков он наберет не более 960 очков, а тогда для того, чтобы набрать 1001 очко понадобится не менее 17 бросков.
Покажем, что игрок может набрать 1001 очко за 17 бросков. Предположим, что он сделал 15 бросков на 60 очков (итого 900), один бросок в зону утроения сектора 17 (51 очко) и один бросок в центральный сектор 50 очков. Тогда в сумме он наберет 900 + 51 + 50 = 1001 очко.
Ответ: а) да; б) нет; в) 17.
-
Задание 11
Семь экспертов оценивают кинофильм. Каждый из них выставляет оценку — целое число баллов от 0 до 10 (от 1 до 15) включительно. Известно, что все эксперты выставили различные оценки. По старой системе оценивания рейтинг кинофильма — это среднее арифметическое всех оценок экспертов. По новой системе оценивания рейтинг кинофильма вычисляется следующим образом: отбрасываются наименьшая и наибольшая оценки и подсчитывается среднее арифметическое пяти оставшихся оценок.
а) Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться

б) Может ли эта разность рейтингов, вычисленных по старой и новой системам оценивания, равняться

в) Найдите наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания.
Разбор задания
СвернутьОбозначим рейтинг кинофильма, вычисленный по старой системе оценивания, через A, а рейтинг кинофильма, вычисленный по новой системе оценивания, через B.
а) Заметим, что
 где m и n — некоторые натуральные числа.
где m и n — некоторые натуральные числа.Значит,
 Если
Если  то
то  что невозможно.
что невозможно.Таким образом, разность рейтингов, вычисленных по старой и новой системам оценивания, не может равняться

б) Например, для оценок экспертов 0, 1, 2, 4, 7, 8, 9 разность рейтингов, вычисленных по старой и новой системам оценивания, равна

в) Пусть x — наименьшая из оценок, z — наибольшая, а y — сумма остальных пяти оценок. Тогда


Для оценок экспертов 0, 1, 2, 3, 4, 5, 10 разность A − B равна 4. Значит, наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания, равно

Ответ: а) нет; б) да; в)
 .
. -
Задание 12
Участники одной школы писали тест. Результатом каждого ученика является целое неотрицательное число баллов. Ученик считается сдавшим тест, если он набрал не менее 83 баллов. Из-за того, что задания оказались слишком трудными, было принято решение всем участникам теста добавить по 5 баллов, благодаря чему количество сдавших тест увеличилось.
а) Могло ли оказаться так, что после этого средний балл участников, не сдавших тест, понизился?
б) Могло ли оказаться так, что после этого средний балл участников, сдавших тест, понизился, и средний балл участников, не сдавших тест, тоже понизился?
в) Известно, что первоначально средний балл участников теста составил 90, средний балл участников, сдавших тест, составил 100, а средний балл участников, не сдавших тест, составил 75. После добавления баллов средний балл участников, сдавших тест, стал равен 103, а не сдавших — 79. При каком наименьшем числе участников теста возможна такая ситуация?
Разбор задания
Свернутьа) Пусть было 3 участника, которые набрали 100, 82 и 2 балла. Средний балл участников, не сдавших тест
 балла. После добавления баллов у участников оказалось 105, 87 и 7 баллов. Средний балл участников, не сдавших тест, составил 7 баллов.
балла. После добавления баллов у участников оказалось 105, 87 и 7 баллов. Средний балл участников, не сдавших тест, составил 7 баллов.б) В примере предыдущего пункта средний балл участников теста, сдавших тест, первоначально составил 100 баллов, а после добавления баллов составил
 баллов.
баллов.в) Пусть всего было N участников теста, сдали тест a участников, после добавления баллов сдали тест b участников. Заметим, что средний балл после добавления составил 95. Имеем два уравнения:
90N = 75(N − a) + 100a и 95N = 79(N − b) + 103b,
откуда 15N = 25a, то есть 3N = 5a, и 16N = 24b, то есть 2N = 3b. Таким образом,
 .
.Покажем, что N могло равняться 15. Пусть изначально 5 участников набрали по 74 балла, 1 участник — 80 баллов и 9 участников по 100 баллов. Тогда средний балл был равен 90, средний бал участников, сдавших тест, был равен 100, а средний балл участников, не сдавших тест, был равен 75. После добавления средний балл участников, сдавших тест, стал равен 103, средний балл участников, не сдавших тест, стал равен 79. Таким образом, все условия выполнены.
Ответ: а) да; б) да; в) 15.
-
Задание 13
Имеются каменные глыбы: 50 штук по 800 кг, 60 штук по 1 000 кг и 60 штук по 1 500 кг (раскалывать глыбы нельзя).
а) Можно ли увезти все эти глыбы одновременно на 60 грузовиках, грузоподъёмностью 5 тонн каждый, предполагая, что в грузовик выбранные глыбы поместятся?
б) Можно ли увезти все эти глыбы одновременно на 38 грузовиках, грузоподъёмностью 5 тонн каждый, предполагая, что в грузовик выбранные глыбы поместятся?
в) Какое наименьшее количество грузовиков, грузоподъёмностью 5 тонн каждый, понадобится, чтобы вывезти все эти глыбы одновременно, предполагая, что в грузовик выбранные глыбы поместятся?
Разбор задания
Свернутьа) Масса любых трёх таких глыб не превосходит 5 тонн. Значит, в 60 грузовиков можно погрузить 180 таких глыб. Всего глыб 170, поэтому их можно увезти на 60 грузовиках.
б) Суммарная масса глыб равна 50 · 800 + 60 · 1000 + 60 · 1500 = 190 000 (кг), то есть в точности совпадает с грузоподъёмностью 38 грузовиков. Значит, если возможно увезти эти глыбы на 38 грузовиках, то каждый грузовик должен быть загружен полностью (по массе груза).
Если в каком-то грузовике есть глыба массой 800 кг, то единственная возможность загрузить такой грузовик полностью — это добавить ещё 4 таких глыбы и одну глыбу массой 1 000 кг. Таким образом, грузовиков, загруженных так, понадобится 10 штук. Поскольку осталось 60 глыб, массой 1 500 кг каждая, и 28 грузовиков, то в одном из грузовиков должно быть хотя бы 3 такие глыбы. Но в грузовик, в который загружено 3 глыбы, массой 1 500 кг каждая, ничего больше погрузить не получится.
Значит, на 38 грузовиках увезти эти глыбы нельзя.
в) В предыдущем пункте было показано, что 38 грузовиков не хватит.
Если в 10 грузовиков загрузить по 5 глыб, массой 800 кг каждая, и глыбу массой 1 000 кг, в 25 грузовиков загрузить по 2 глыбы, массой 1 000 кг каждая, и по 2 глыбы, массой 1 500 кг каждая, в 3 грузовика загрузить
3 глыбы, массой 1 500 кг каждая, и в один грузовик глыбу массой 1 500 кг, то все глыбы окажутся загружены в 39 грузовиков. Значит, наименьшее количество грузовиков — это 39.
Ответ: а) да; б) нет; в) 39.

 Найти сумму положительных и сумму нечетных членов последовательности. Вывести ту сумму, которая по модулю меньше
Найти сумму положительных и сумму нечетных членов последовательности. Вывести ту сумму, которая по модулю меньше Получены точные формулы и оценки сумм модулей коэффициентов Уолша.
Получены точные формулы и оценки сумм модулей коэффициентов Уолша.  mathnet.ru/mvk240}
mathnet.ru/mvk240} 

