Не могу понять принцип
Анастасия
Профи
(532),
на голосовании
3 года назад
Пусть события A и B имеют вероятности 0,5 и 0,7 Найти
Наибольшую вероятность, которую может иметь событие A∪B
Наименьшую вероятность, которую может иметь событие A∪B
Наибольшую вероятность, которую может иметь событие A∩B
Наименьшую вероятность, которую может иметь событие A∩B
Разве наибольшая вероятность это не 1,а наименьшая это произведение или сумма этих чисел?
Голосование за лучший ответ
Ирина Лебедева
Оракул
(83479)
4 года назад
1) Наибольшая вероятность A∪B действительно равна 1
2) Наименьшая вероятность A∪B равна 0,7 (А является подмножеством В)
3) Наибольшая вероятность A∩B равна 0,5 (А является подмножеством В)
4) Наименьшая вероятность A∩B равна 0,2 (из условия 0,7+0,5-Х=1)
АнастасияПрофи (532)
3 года назад
Спасибо!
Ирина Лебедева
Оракул
(83479)
Пожалуйста:) Вопросы были необычные и потому интересные
Смысл вопроса хотелось бы уточнить. Дело в том, что можно говорить о наименьшем и наибольшем значении вообще, то есть по всевозможным парам таких событий $%A$% и $%B$%, а можно — при фиксированных значениях величин $%P(A)$% и $%P(B)$%. Первая трактовка не слишком интересна, потому что при ней $%P(Acap B)$% всегда принимает строго положительные значения, но они могут быть сколь угодно близки к нулю. Поэтому наименьшее значение здесь не достигается, а про наибольшее можно сказать, что оно равно единице.
При второй трактовке рассуждение такое. Поскольку $%P(Acap B)=P(A)+P(B)-P(Acup B)$%, рассматриваемое значение вероятности не меньше $%P(A)+P(B)-1$%. Это наименьшее возможное значение; оно строго положительно по условию. Оно достигается, если $%Acup B$% — полное событие, чего всегда можно добиться. Наибольшее значение равно $%min(P(A),P(B))$%. Ясно, что $%Acap B$% содержится как в $%A$%, так и в $%B$%, то есть вероятность пересечения двух событий не превосходит вероятности каждого из них, а потому и минимума этих вероятностей. Это значение достигается, когда одно из событий $%A$%, $%B$% содержится в другом.
● Классическая формула сложения
вероятностей
-
Независимо
друг от друга 5 человек садятся в поезд,
содержащий 13 вагонов. Найдите вероятность
того, что все они поедут в разных вагонах.

-
В партии
из 13 деталей имеется 8 стандартных.
Наудачу отобраны 7 деталей. Найдите
вероятность того, что среди отобранных
деталей ровно 5 стандартных.
![]()

-
В киоске
продается 9 лотерейных билетов, из
которых число выигрышных составляет
3 штуки. Студент купил 4 билета. Какова
вероятность того, что число выигрышных
среди них будет не меньше 2, но не больше
3?
|
Всего |
Выигрыш |
Проигрыш |
|
|
Было |
9 |
3 |
6 |
|
Отобрано |
4 |
2 |
2 |
|
Отобрано |
4 |
3 |
1 |

-
В группе
учатся 13 юношей и 9 девушек. Для дежурства
случайным образом отобраны три студента.
Найдите вероятность того, что все
дежурные окажутся юношами.

-
Имеется
25 экзаменационных билетов, на каждом
из которых напечатано условие некоторой
задачи. В 15 билетах задачи по статистике,
а в остальных 10 билетах задачи по теории
вероятностей. Трое студентов выбирают
наудачу по одному билету. Найдите
вероятность того, что хотя бы одному
из них не достанется задачи по теории
вероятностей.

-
В ящике
3 белых и 4 черных шаров. Найдите
вероятность того, что из двух вынутых
наудачу шаров один белый, а другой
черный. Вынутый шар в урну не возвращается.

-
В ящике
12 шаров, из них 3 белых, а остальные –
черные. Из ящика наугад берут 5 шаров.
Какова вероятность, что среди выбранных
есть хотя бы один белый шар?

●
Геометрические вероятности
-
В квадрат
со стороной 15м случайным образом
вбрасывается точка. Найдите вероятность
того, что эта точка окажется в правой
верхней четверти квадрата или не далее,
чем на 2м от центра квадрата.

-
На
отрезок
 длины 240 наудачу поставлена точка
длины 240 наудачу поставлена точка .
.
Найдите вероятность того, что меньший из отрезков
того, что меньший из отрезков и
и имеет длину большую, чем 48.
имеет длину большую, чем 48.
![]()
-
На
отрезок
 длины 120 наудачу поставлена точка
длины 120 наудачу поставлена точка .
.
Найдите вероятность того, что меньший из отрезков
того, что меньший из отрезков и
и имеет длину меньшую, чем 30.
имеет длину меньшую, чем 30.
![]()
-
На
плоскости начерчены две концентрические
окружности, радиусы которых 20 и 100
соответственно. Найдите вероятность
того, что точка, брошенная наудачу в
большой круг, попадет также и в кольцо,
образованное построенными окружностями.
![]()
-
Внутрь
круга радиуса 50 наудачу брошена точка.
Какова вероятность того, что точка
окажется внутри вписанного в круг
квадрата? правильного треугольника?
правильного шестиугольника?

-
Двое
договорились о встрече между 6 и 7 часами
утра, причем договорились ждать друг
друга не более 5 минут. Считая, что момент
прихода на встречу выбирается каждым
наудачу в пределах указанного часа,
найти вероятность того, что встреча
состоится.

-
В шар
радиуса 150 наудачу бросаются 2 точки.
Найдите вероятность того, что расстояние
от центра шара до ближайшей точки будет
не меньше 120.

-
В круг
радиуса 150 наудачу бросаются 4 точки.
Найдите вероятность того, что расстояние
от центра круга до ближайшей точки
будет не меньше 75.
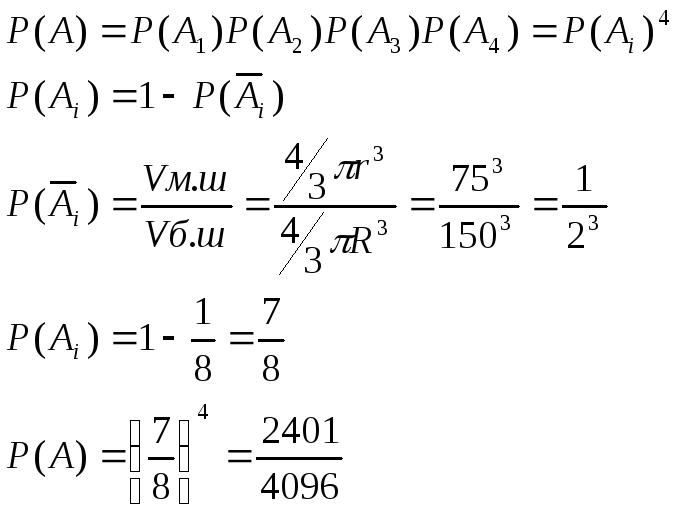
-
В шар
радиуса 100 наудачу бросаются 4 точки.
Найдите вероятность того, что расстояние
от центра шара до самой удаленной точки
будет не больше 50.

●
Правила сложения и умножения
вероятностей
-
Пусть
 – вероятности событий. Найдите наименьшую
– вероятности событий. Найдите наименьшую
возможную вероятность события .
.

-
Вероятность
события
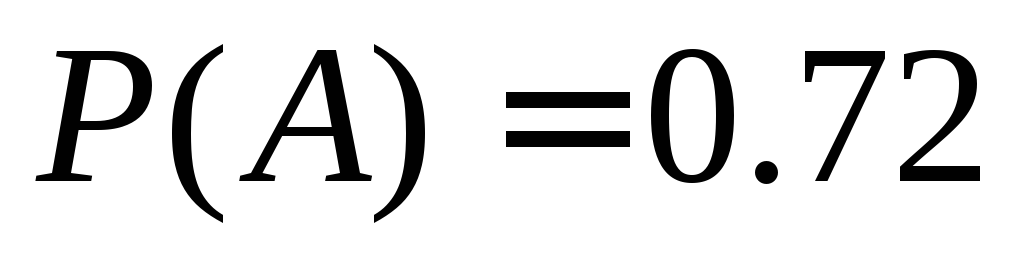 ,
, ,
, Найдите наименьшую возможную вероятность
Найдите наименьшую возможную вероятность
события .
.

-
В
электрическую цепь последовательно
включены три элемента, работающие
независимо один от другого. Вероятности
отказов первого, второго и третьего
элементов соответственно равны
 ,
, и
и .
.
Найдите вероятность того, что тока в
цепи не будет.
А-событие, сост. в том, что тока нет
![]() -событие,
-событие,
сост. в том, что ток есть
![]() =В1,В2,В3
=В1,В2,В3
Вi-событие, сост.
в том, что прибор исправен

-
Вероятность
хотя бы одного попадания в мишень при
9 выстрелах равна 0.81. Найдите вероятность

попадания при одном выстреле.
А-событие,
сост. в том, что при 9 выстрелах в мишень
попадут 1 раз
P(A)=0.81
А с
чертой – событие, сост. в том, что в
мишень не попали ни разу
Вероятность
непопадания при 1 выстреле
![]()
След, вероятность попадания 1 выстрела
![]()
-
Пассажир
подходит к остановке автобусов двух
маршрутов. Интервал движения автобусов
1-го маршрута составляет
 мин., а 2-го маршрута –
мин., а 2-го маршрута – мин. Найдите вероятность того, что
мин. Найдите вероятность того, что
пассажир уедет с остановки не позднее,
чем через мин., считая, что его устроит автобус
мин., считая, что его устроит автобус
как 1-го, так и 2-го маршрутов.
А-событие, сост. В том, что уедет не
позднее, чем через 6 мин
![]() -опоздает
-опоздает
![]()
В-1
авт. Прибудет позднее 6 мин
С –
2 авт. Прибудет позднее 6 мин

-
В ящике
8 белых и 13 черных шаров. Два игрока
поочередно извлекают по шару, каждый
раз возвращая его обратно. Выигрывает
тот, кто первым вытащит белый шар. Какова
вероятность выигрыша для начинающего
игру?
А-событие,
сост. в том, что достали белый шар

-
Вероятность
того, что при одном измерении некоторой
физической величины допущена ошибка,
равна 0.05. Найдите наименьшее число
 измерений,
измерений,
которые необходимо произвести, чтобы
с вероятностью можно было ожидать, что хотя бы один
можно было ожидать, что хотя бы один
результат измерений окажется неверным.
А-хотя бы 1 раз результат окажется
неверным
А с чертой- все верны
А с чертой= В1, …Вn
Bi– где i
результат верен

●
Формула полной вероятности. Формула
Байеса
-
В ящике
содержатся
 деталей, изготовленных на заводе 1,
деталей, изготовленных на заводе 1, деталей – на заводе 2 и
деталей – на заводе 2 и деталей – заводе 3. Вероятности
деталей – заводе 3. Вероятности
изготовления брака на заводах с номерами
1, 2 и 3 соответственно равны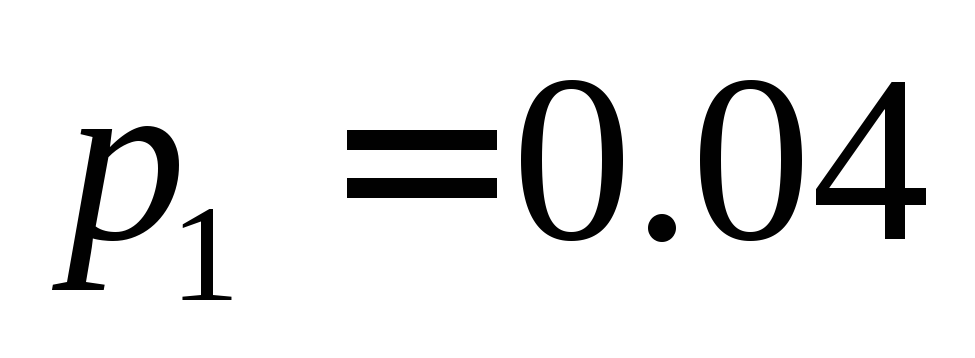 ,
, и
и .
.
Найдите вероятность того, что извлеченная наудачу деталь
того, что извлеченная наудачу деталь
окажется качественной.
Hi–
гипотеза, что деталь изготовлена на i
заводе
P(Hi)-вероятность
того, что деталь изготовлена на 1 заводе

-
В урну,
содержащую
 шаров, опущен белый шар, после чего
шаров, опущен белый шар, после чего
наудачу извлечен один шар. Найдите
вероятность того, что извлеченный шар
окажется белым, если равновероятны все
возможные предположения о первоначальном
количестве белых шаров в урне.
Hi-первоначально
в урне i белых
шаров
i=0,….20
А-
событие, сост, в том, что извлечен белый
шар
![]()
![]()
-
В первой
урне 5 белых и 3 черных шара, во второй
– 6 белых и 9 черных. Из второй урны
случайным образом перекладывают в
первую два шара, после чего из первой
урны берут один шар. Какова вероятность
того, что этот шар – белый?

-
С первого
станка-автомата на сборочный конвейер
поступает
 деталей, со 2-го и 3-го – по
деталей, со 2-го и 3-го – по и
и соответственно. Вероятности выдачи
соответственно. Вероятности выдачи
бракованных деталей составляют для
каждого из них соответственно ,
, и
и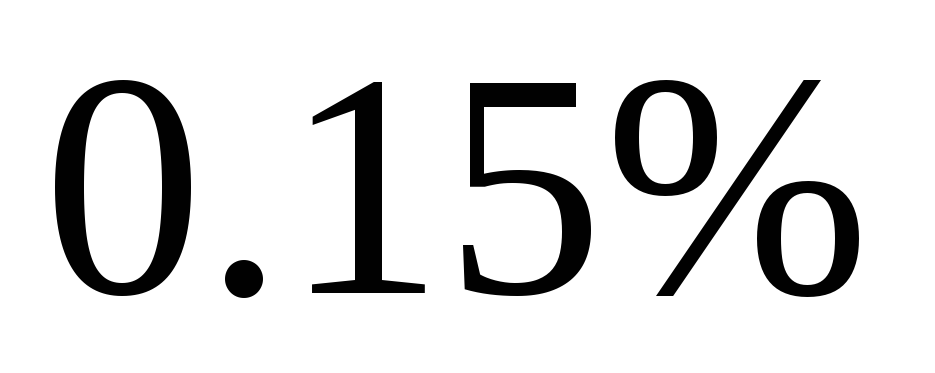 .
.
Найдите вероятность того, что поступившая
на сборку деталь окажется бракованной,
а также вероятности того, что она
изготовлена на 1-м, 2-м и 3-м станках-автоматах,
при условии, что она оказалась бракованной.

-
Имеется
три одинаковых по виду ящика. В первом
ящике 23 белых шара, во втором – 9 белых
и 14 черных шаров, в третьем – 23 черных
шара. Из выбранного наугад ящика вынули
белый шар. Найдите вероятность того,
что шар вынут из второго ящика.
![]()
|
1 |
2 |
3 |
|
|
Кол-во |
23 |
23 |
23 |
|
% |
1/3 |
1/3 |
1/3 |
|
Кол-во |
23 |
9 |
0 |
|
% |
1 |
9/23 |
0 |

-
В среднем
из 100 клиентов банка 53 обслуживаются
первым операционистом и 47 – вторым.
Вероятности того, что клиент будет
обслужен без помощи заведующего
отделением, только самим операционистом,
составляет
 и
и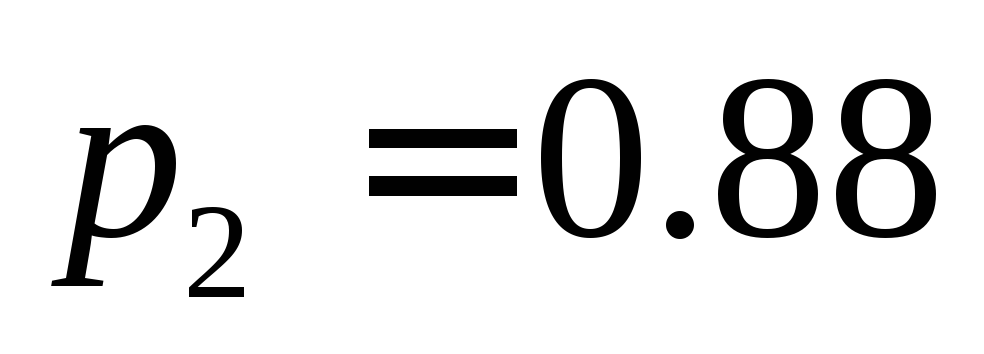 соответственно для первого и второго
соответственно для первого и второго
служащих банка. Какова вероятность,
что клиент, для обслуживания которого
потребовалась помощь заведующего, был
направлен к первому операционисту?
n1-1-ый
операционист
n2-2-ой
операционист
А-событие,
сост. в том, что, что потребуется помощь
заведующего

-
Имеется
13 монет, из которых 3 штуки бракованные:
вследствие заводского брака на этих
монетах с обеих сторон отчеканен герб.
Наугад выбранную монету, не разглядывая,
бросают 9 раз, причем при всех бросаниях
она ложится гербом вверх. Найдите
вероятность того, что была выбрана
монета с двумя гербами.
H1-монета
хорошая
H2
– бракованная монета
А-событие,
состю в том, что при всех бросании монета
легла гербом

-
Детали,
изготовленные в цехе, попадают к одному
из 2-х контролёров. Вероятность того,
что деталь попадёт к 1-му контролёру,
равна 0,8; ко 2-му – 0,2. Вероятность того,
что годная деталь будет признана
стандартной 1-м контролёром равна 0,96;
2-м контролёром – 0,98. Годная деталь при
проверке оказалась стандартной. Найдите
вероятность того, что эту деталь проверял
1-й контролёр.

-
Пассажир
может обратиться за получением билета
в одну из трёх касс (А,B,C). Вероятности
обращения в каждую кассу зависят от их
местонахождения и равны соответственно
0,4;0,5 и 0,1. Вероятности того, что к моменту
прихода пассажира, имеющиеся в кассе
билеты распроданы равны соответственно
0,4; 0,3 и 0,1. Найдите вероятность того, что
билет куплен. В какой из касс это могло
произойти с наибольшей вероятностью?
![]()

-
В первой
урне
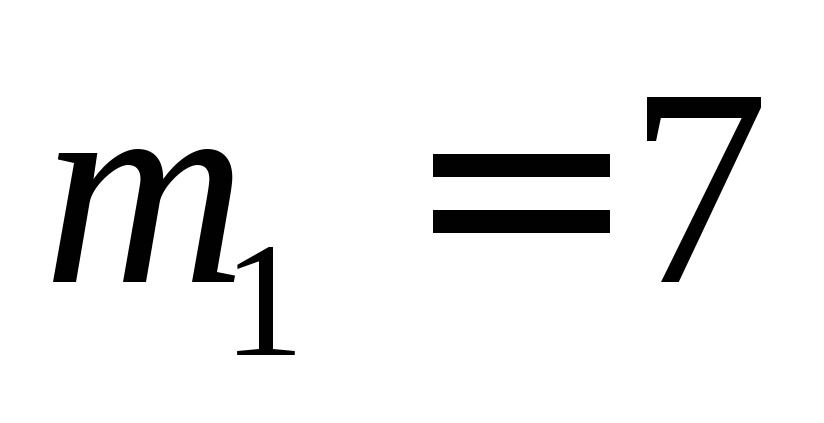 белых и
белых и черных шаров, во второй –
черных шаров, во второй – белых и
белых и черных. Из второй урны случайным образом
черных. Из второй урны случайным образом
перекладывают в первую два шара, после
чего из первой урны берут один шар,
который оказывается белым. Какова
вероятность того, что два шара,
переложенные из второй урны в первую,
были разных цветов?

●
Схема Бернулли. Числа
![]() .
.
Наиболее вероятное число успехов
-
Вероятность
попадания в цель при одном выстреле
равна
 .
.
Сделано выстрелов. Найдите вероятность того,
выстрелов. Найдите вероятность того,
что в цель попали менее трех раз.

-
Отрезок
длины
 поделен на две части длины
поделен на две части длины и
и соответственно,
соответственно, точек последовательно бросают случайным
точек последовательно бросают случайным
образом на этот отрезок. Найдите
вероятность того, что количество точек,
попавших на отрезок длины будет больше или меньше
будет больше или меньше .
.
М-событие, сост. в том, что на отрезок
АС попало не менее 2 точек
М с чертой – событие, сост. в том, что
попало 2 точки
Р – вероятность попадания на АС при
1 бросании

-
Вероятность
попадания стрелком в цель равна
 .
.
Сделано выстрелов. Определите наивероятнейшее
выстрелов. Определите наивероятнейшее
число попаданий в цель.

●
Схема Бернулли. Приближенные формулы
Лапласа и Пуассона
-
Вероятность
выпуска бракованного изделия равна
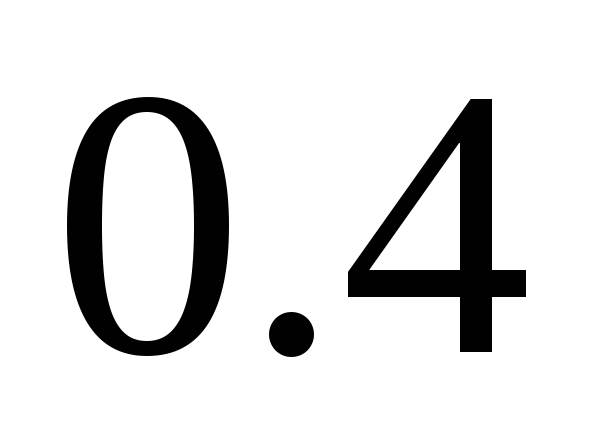 .
.
Найдите вероятность того, что среди выпущенных изделий ровно
выпущенных изделий ровно изделий без брака.
изделий без брака.

-
Вероятность
выпуска бракованного изделия равна
 .
.
Найдите вероятность того, что среди
того, что среди выпущенных изделий будет хотя бы одно,
выпущенных изделий будет хотя бы одно,
но не более бракованных изделий.
бракованных изделий.

-
Всхожесть
семян данного растения равна
 .
.
Найдите вероятность того, что из
того, что из посаженных семян число проросших семян
посаженных семян число проросших семян
заключено между и
и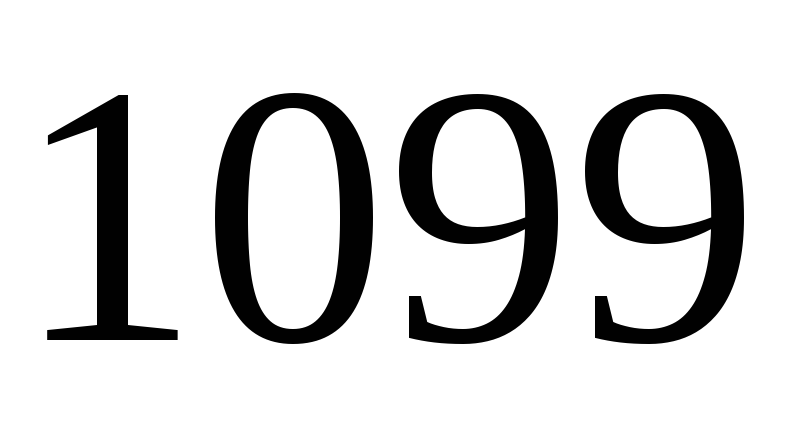 .
.

-
Прядильщица
обслуживает
 веретен. Вероятность обрыва нити на
веретен. Вероятность обрыва нити на
одном веретене в течение 1 минуты равна .
.
Найдите вероятность того, что в течение одной минуты обрыв
того, что в течение одной минуты обрыв
произойдет более чем на веретенах.
веретенах.
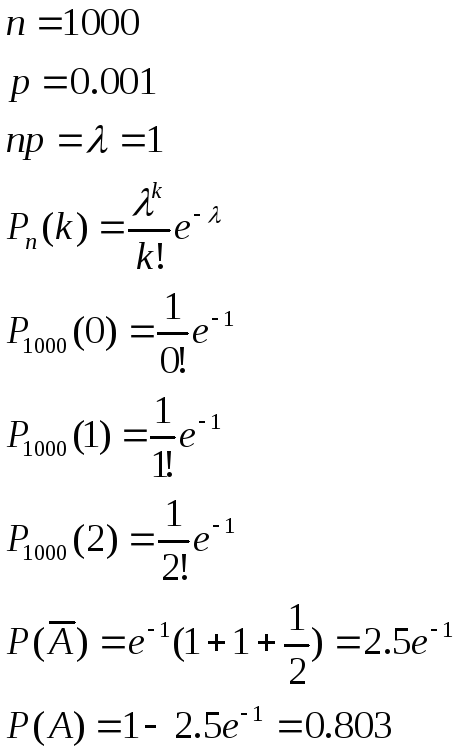

-
Завод
отправил на базу
 доброкачественных
доброкачественных
изделий. Вероятность того, что в пути
изделие повредится, равна .
.
Какова вероятность того, что на базу поступят
того, что на базу поступят некачественных изделия?
некачественных изделия?

-
При
введении вакцины против полиомиелита
иммунитет создается в
 случаях. Определите вероятность
случаях. Определите вероятность того, что из
того, что из вакцинированных детей заболеют
вакцинированных детей заболеют .
.

●
Закон распределения случайной
величины
-
Случайная
величина
 принимает только целые значения
принимает только целые значения
 .
.
При этом вероятности возможных значений пропорциональны значениям:
пропорциональны значениям: .
.
Найдите значение константы и вероятность
и вероятность .
.
|
X |
1 |
2 |
3 |
…. |
k |
… |
28 |
|
P |
c |
2c |
3c |
…. |
kc |
… |
28c |
C(1+2+…+28)=1

-
Случайная
величина
 принимает только целые неотрицательные
принимает только целые неотрицательные
значения .
.
При этом .
.
Найдите значение константы и вероятность
и вероятность .
.
|
X |
0 |
1 |
2 |
… |
k |
|
P |
c |
c/6 |
c/6^2 |
… |
c/6^k |
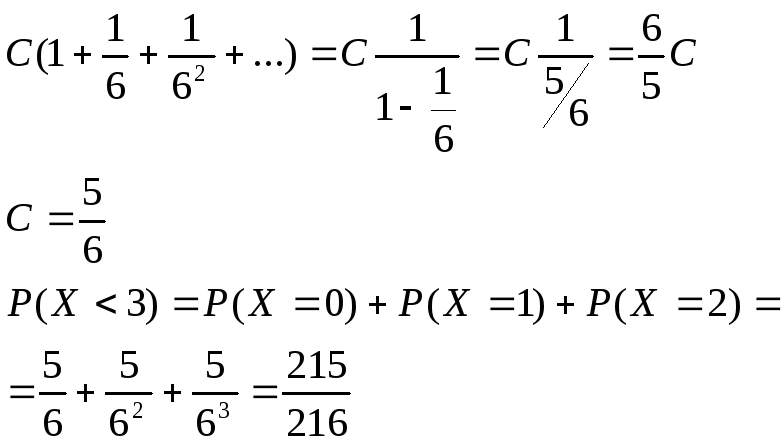
● Независимые
дискретные случайные величины
-
Независимые
дискретные случайные величины
 принимают только целые значения:
принимают только целые значения: – от
– от до
до с вероятностью
с вероятностью ,
, – от
– от до
до с вероятностью
с вероятностью .
.
Найдите вероятность .
.

-
Независимые
случайные величины
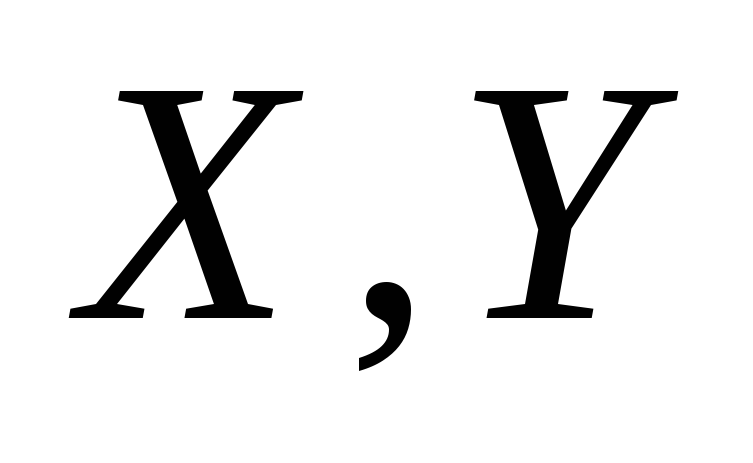 принимают только целые значения:
принимают только целые значения: – от
– от до
до с вероятностью
с вероятностью ,
, – от
– от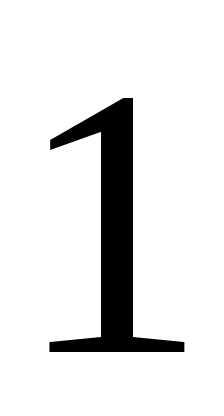 до
до с вероятностью
с вероятностью .
.
Найдите вероятность .
.

-
Независимые
случайные величины
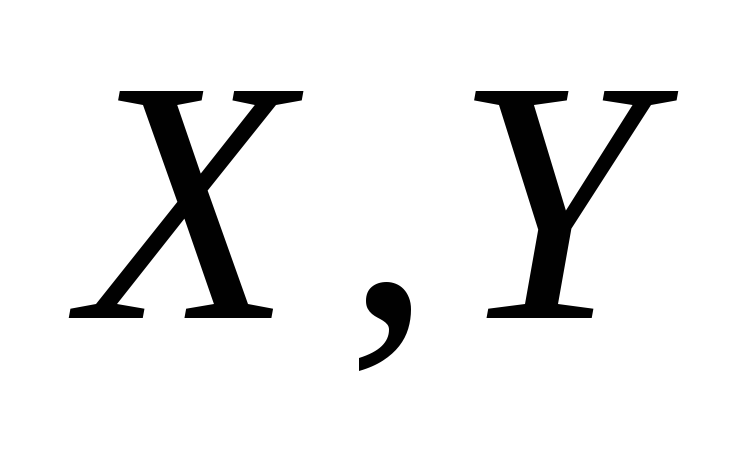 принимают только целые значения:
принимают только целые значения: – от
– от до
до с вероятностью
с вероятностью ,
, – от
– от до
до с вероятностью
с вероятностью .
.
Найдите вероятность .
.

-
Независимые
случайные величины
 принимают только целые значения:
принимают только целые значения: – от
– от до
до с вероятностью
с вероятностью ,
, – от
– от до
до с вероятностью
с вероятностью .
.
Найдите вероятность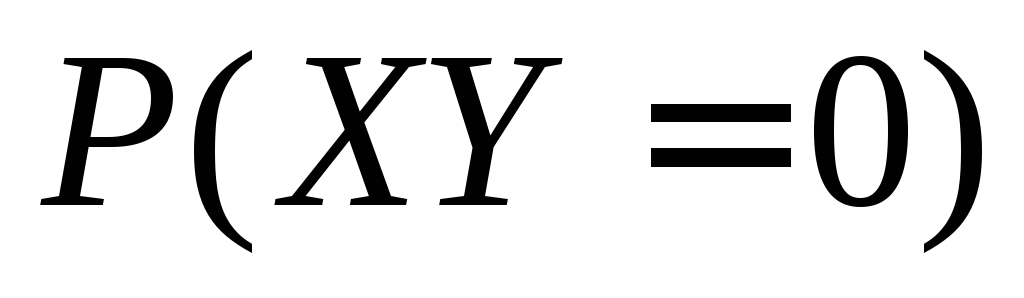 .
.
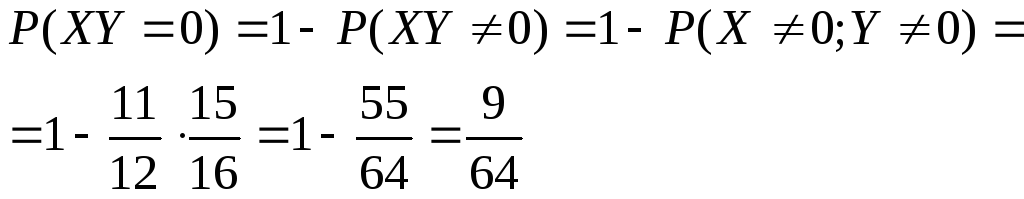
-
Независимые
случайные величины
 и
и принимают только целые значения:
принимают только целые значения: – от
– от до
до ,
, – от
– от до
до .
.
Найдите ,
,
если известно, что возможные значения и
и равновероятны.
равновероятны.
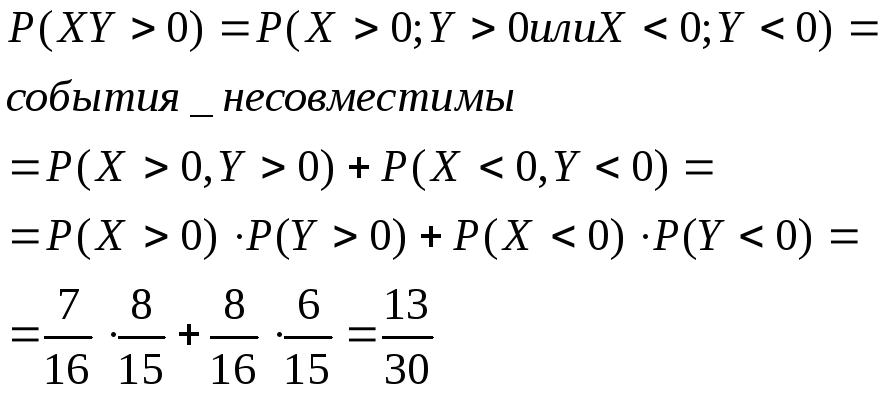
-
Независимые
случайные величины
 принимают только целые значения:
принимают только целые значения: – от
– от до
до с вероятностью
с вероятностью ,
, – от
– от до
до с вероятностью
с вероятностью .
.
Найдите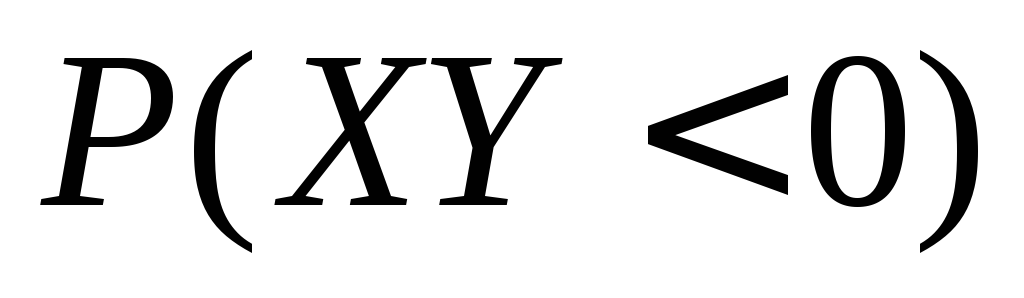 .
.

-
Независимые
случайные величины
 принимают только целые значения от
принимают только целые значения от до
до .
.
Найдите вероятность ,
,
если известно, что все возможные значения
равновероятны.

-
Независимые
случайные величины
 принимают только целые значения:
принимают только целые значения: – от
– от до
до с вероятностью
с вероятностью ,
, – от
– от до
до с вероятностью
с вероятностью ,
, – от
– от до
до с вероятностью
с вероятностью .
.
Найдите вероятность того, что примут разные значения.
примут разные значения.

-
Независимые
случайные величины
 принимают только целые значения:
принимают только целые значения: – от
– от до
до с вероятностью
с вероятностью ,
, – от
– от до
до с вероятностью
с вероятностью ,
, – от
– от до
до с вероятностью
с вероятностью .
.
Найдите вероятность .
.

● Математическое
ожидание и дисперсия дискретной случайной
величины
-
Распределение
дискретной случайной величины
 задано таблицей
задано таблицей
Найдите
математическое ожидание
![]() и вероятность
и вероятность![]() .
.

-
Дискретная
случайная величина
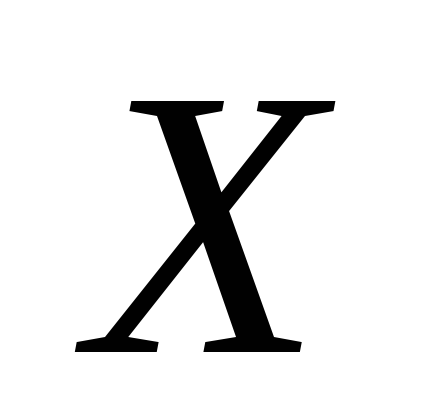 принимает только целые значения
принимает только целые значения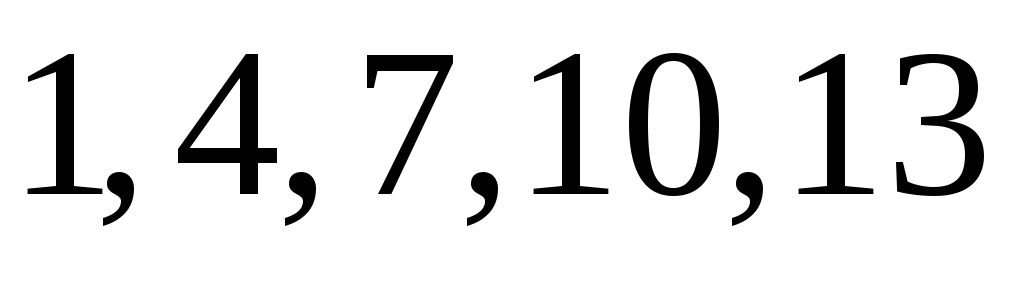 ,
,
каждое с вероятностью .
.
Найдите математическое ожидание и вероятность
и вероятность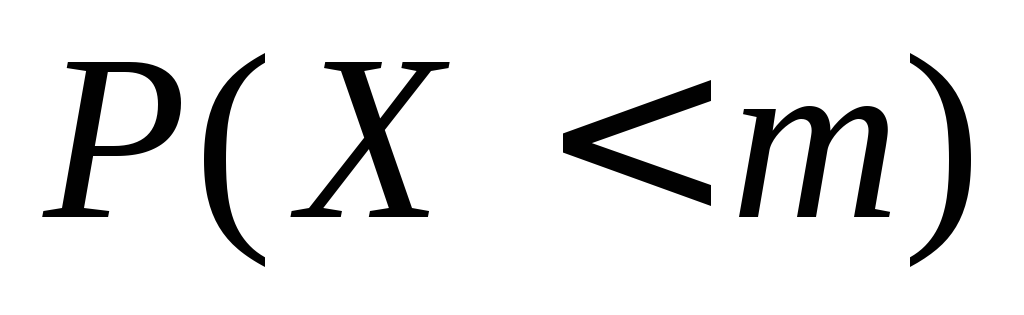 .
.
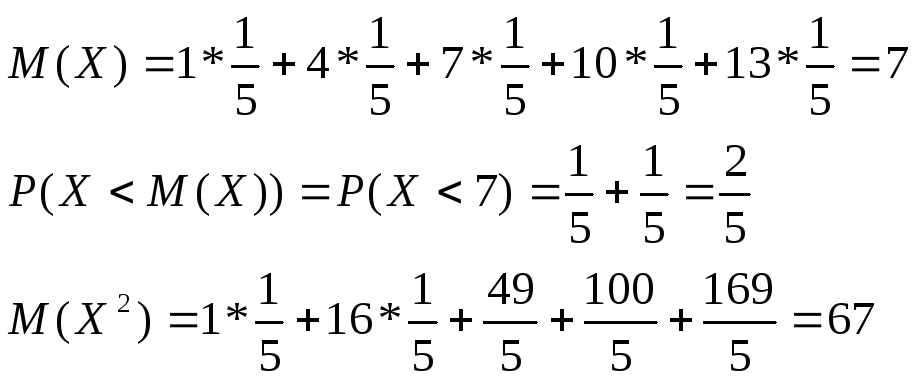
-
Распределение
дискретной случайной величины
 задано таблицей
задано таблицей
Найдите
дисперсию
![]() .
.

-
Распределение
случайной величины
 задано таблицей
задано таблицей
Найдите
математическое ожидание
![]() ,
,
среднее квадратичное отклонение![]() и вероятность
и вероятность![]() .
.

-
Для
случайной величины
 известно, что
известно, что
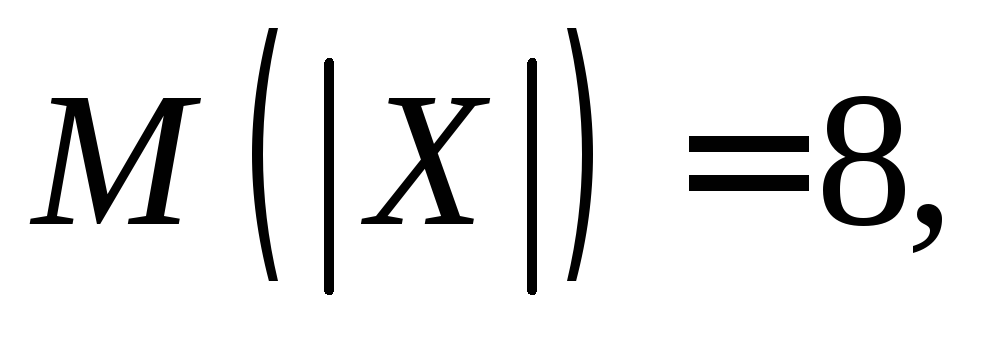
 .
. Найдите дисперсию
Найдите дисперсию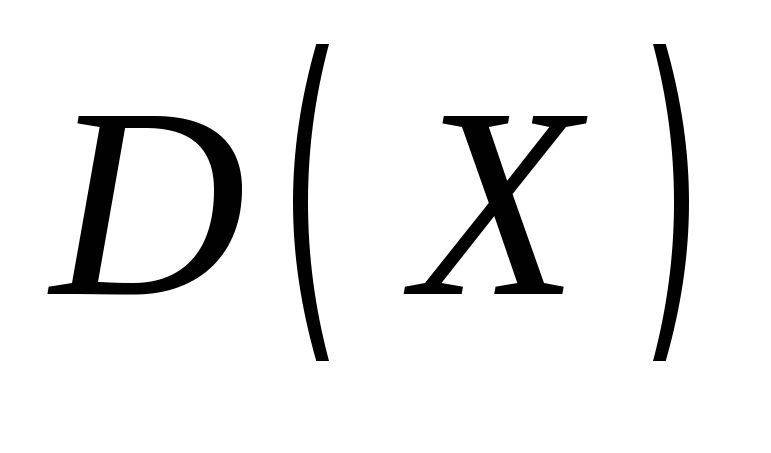 .
.

-
Независимые
дискретные случайные величины
 могут принимать только значения
могут принимать только значения и
и .
.
При этом ,
,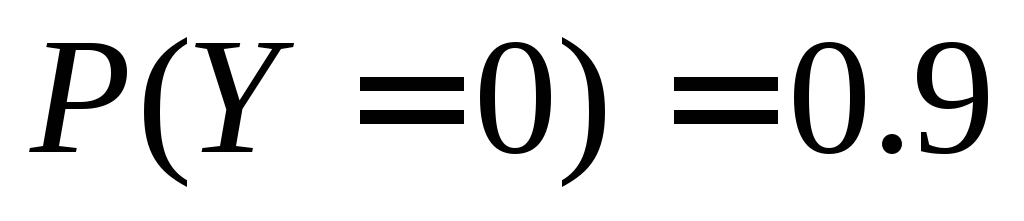 .
.
Найдите математическое ожидание .
.
|
X |
0 |
1 |
Y |
0 |
1 |
|
P |
0.1 |
0.9 |
P |
0.9 |
0.1 |

-
Независимые
дискретные случайные величины
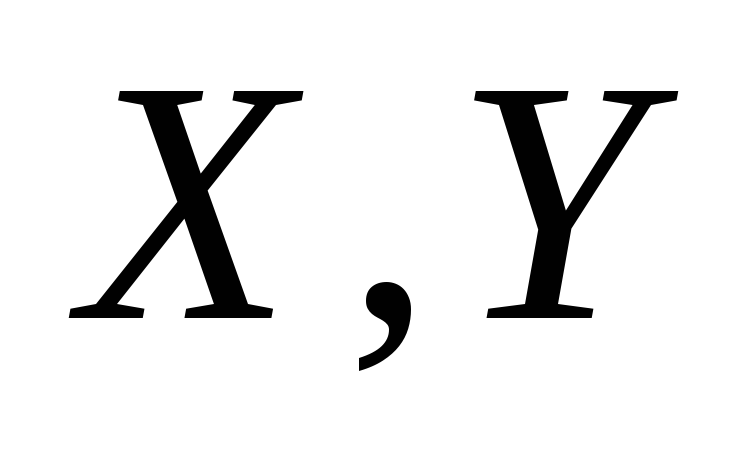 могут принимать только значения
могут принимать только значения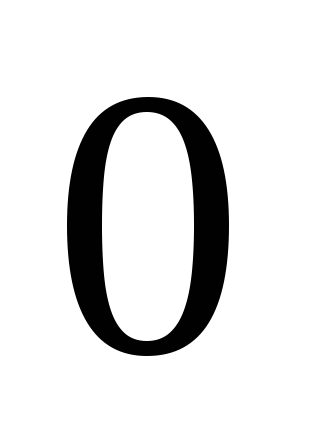 и
и .
.
При этом ,
, .
.
Найдите математическое ожидание .
.
|
X |
0 |
1 |
Y |
0 |
1 |
|
P |
0.1 |
0.9 |
P |
0.6 |
0.4 |

-
Дискретные
случайные величины
 распределены по закону, заданному
распределены по закону, заданному
таблицей
Найдите
математическое ожидание
![]() .
.

-
Независимые
случайные величины
 принимают только целые значения
принимают только целые значения .
.
Найдите математическое ожидание ,
,
если известно, что возможные значения
равновероятны.
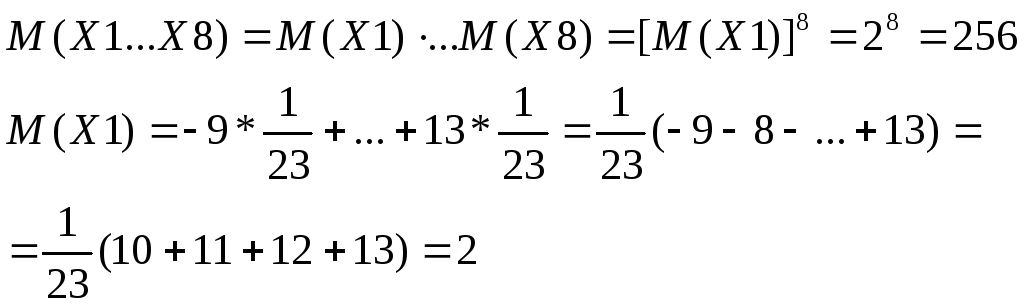
-
Для
независимых случайных величин
 известно, что их математические ожидания
известно, что их математические ожидания ,
,
дисперсии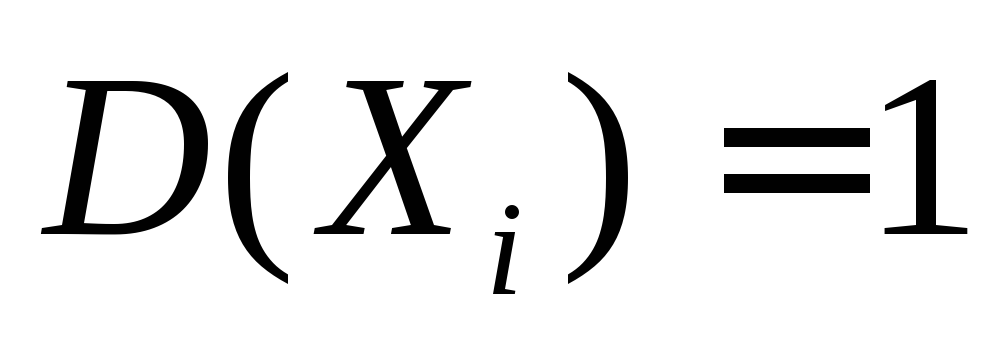 ,
, .
.
Найдите дисперсию произведения .
.

-
Независимые
случайные величины
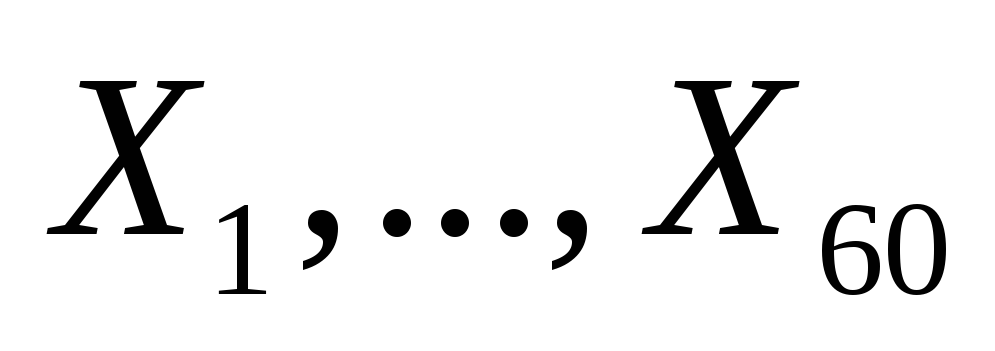 могут принимать только значения
могут принимать только значения и
и .
.
При этом ,
,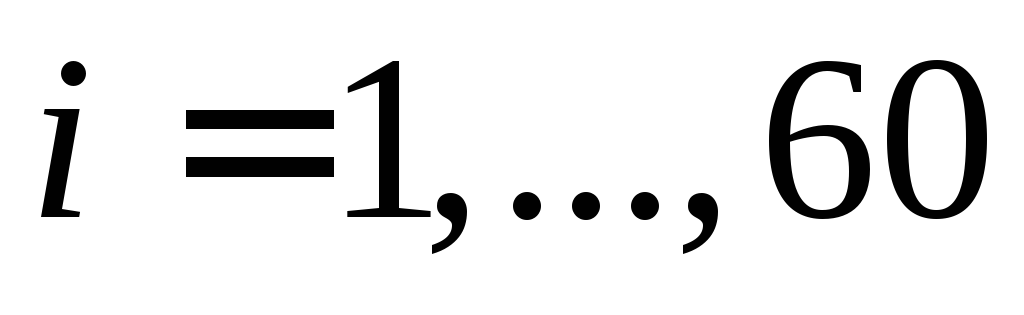 .
.
Найдите математическое ожидание .
.
|
Xi |
0 |
1 |
|
P |
0.9 |
0.1 |

-
Независимые
случайные величины
 могут принимать только значения
могут принимать только значения и
и .
.
При этом ,
, .
.
Найдите математическое ожидание .
.

-
Вероятность
выигрыша
 рублей в одной партии равна
рублей в одной партии равна ,
,
вероятность проигрыша рублей равна
рублей равна .
.
Найдите дисперсию капитала игрока
после партий.
партий.
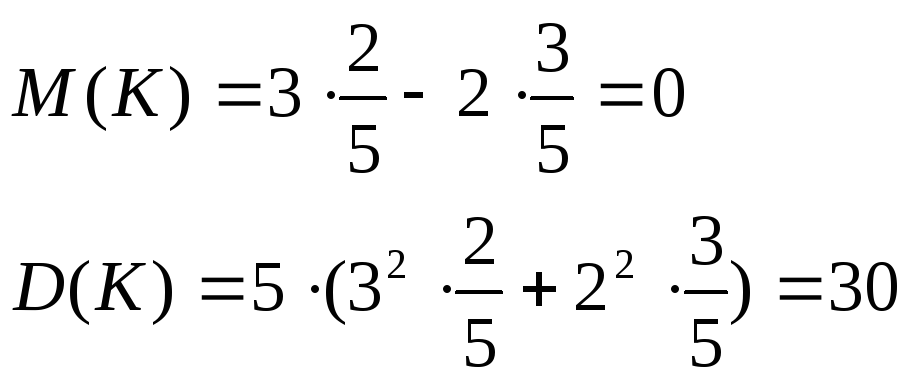
● Основные
дискретные законы распределения и их
характеристики
-
На
плоскости начерчены две окружности,
радиусы которых
 и
и соответственно. Меньшая окружность
соответственно. Меньшая окружность
содержится внутри большего круга. В
большой круг наудачу бросают точек. Пусть случайная величина
точек. Пусть случайная величина – число точек, попавших в малый круг.
– число точек, попавших в малый круг.
Вычислите математическое ожидание и дисперсию
и дисперсию .
.

-
Производится
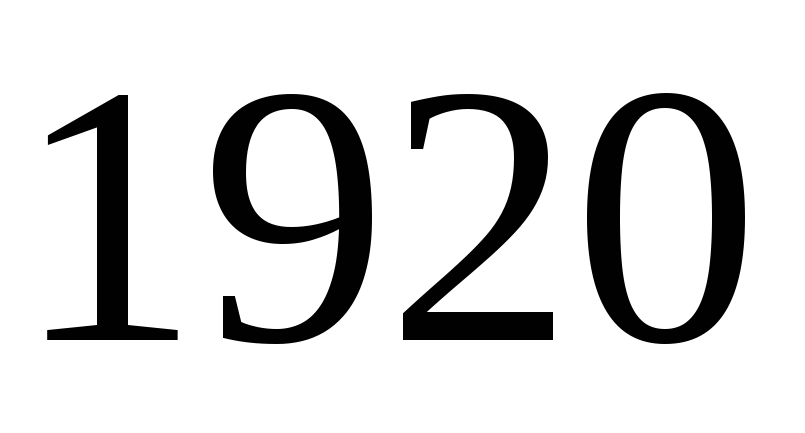 независимых испытаний, состоящих в
независимых испытаний, состоящих в
том, что одновременно подбрасываются монет. Пусть
монет. Пусть – число испытаний, в которых выпало
– число испытаний, в которых выпало герба. Найдите математическое ожидание
герба. Найдите математическое ожидание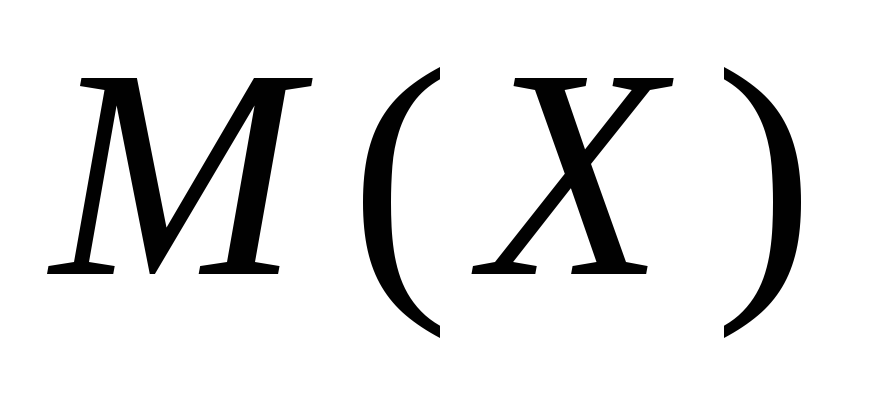 .
.
![]() –число испытаний, в которых выпало
–число испытаний, в которых выпало
![]() герба.
герба.

-
Случайные
величины
 распределены по биномиальному
распределены по биномиальному
закону с
параметрами
![]() и
и![]() .
.
Найдите математическое ожидание![]() .
.

-
Случайные
величины
 независимы и распределены по биномиальному
независимы и распределены по биномиальному
закону с параметрами и .
и .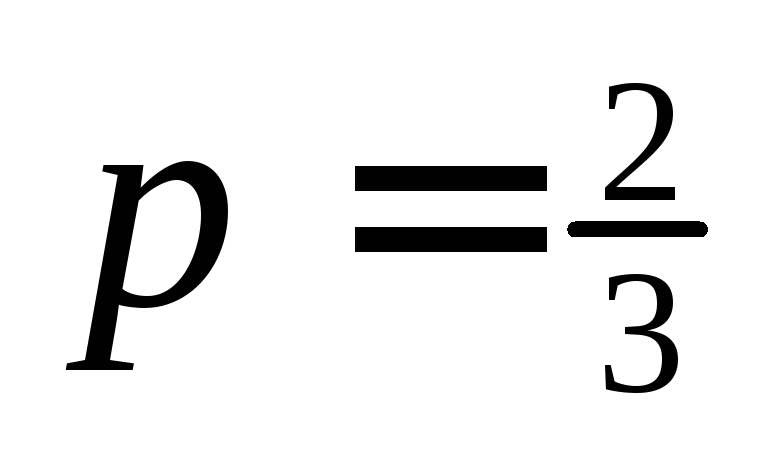 Найдите математическое ожидание
Найдите математическое ожидание .
.
-
Отрезок
длины
 поделен на две части длины
поделен на две части длины и
и соответственно. Наудачу
соответственно. Наудачу точек последовательно бросают на
точек последовательно бросают на
отрезок. – случайная величина, равная числу
– случайная величина, равная числу
точек, попавших на отрезок длины .
.
Найдите математическое ожидание и
среднее квадратичное отклонение
величины .
.

-
Производится
 независимых испытаний, в каждом из
независимых испытаний, в каждом из
которых подбрасываются игральные кости. Пусть
игральные кости. Пусть – число испытаний, в которых все выпавшие
– число испытаний, в которых все выпавшие
цифры оказались .
.
Найдите дисперсию .
.

-
Производится
 независимых испытаний с вероятностью
независимых испытаний с вероятностью
успеха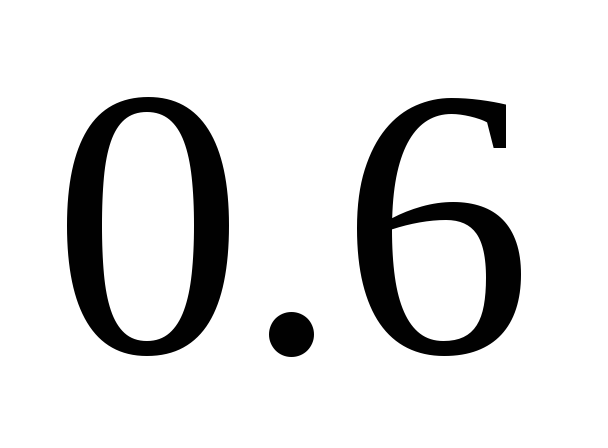 в каждом испытании. Пусть
в каждом испытании. Пусть – число успехов в испытаниях с номерами
– число успехов в испытаниях с номерами ,
, – число успехов в испытаниях с номерами
– число успехов в испытаниях с номерами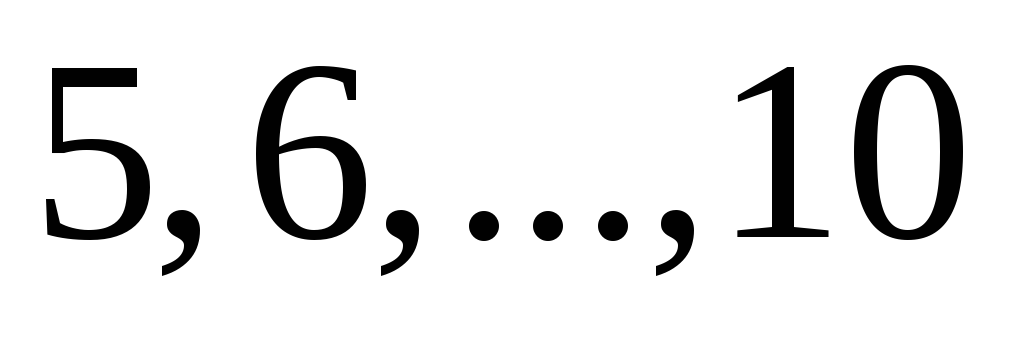 .
.
Найдите дисперсию .
.
U– число успехов в
испытаниях с номерами 1,2,3,4
V– число успехов в
испытаниях с номерами 5,6,7
W– число успехов в
испытаниях с номерами 8.9.10.
Каждая из величин имеет биномиальное
распределение

-
На
плоскости начерчены два квадрата,
стороны которых
 и
и соответственно. Меньший квадрат
соответственно. Меньший квадрат
содержится внутри большего квадрата.
В большой квадрат случайным образом
бросают точки до тех пор, пока не попадут
в маленький квадрат. Пусть случайная
величина – число бросаний. Найдите математическое
– число бросаний. Найдите математическое
ожидание и дисперсию
и дисперсию .
.
Геометрическое распределение

-
В
спортивной лотерее каждую неделю на
100 билетов разыгрывается
 палаток и
палаток и рюкзаков. Турист решил каждую неделю
рюкзаков. Турист решил каждую неделю
покупать по одному билету до тех пор,
пока он не выиграет палатку и рюкзак.
Найдите среднее время реализации
данного намерения (время измеряется в
неделях).
T-время ожидания
T=T1+T2
T1, T2-независимы
Т1-время ожидания 1-го выигрыша
Т2-время ожидания др. выигрыша

-
В серии
независимых испытаний, которые проводятся
с частотой одно испытание в единицу
времени, вероятность наступления
события
 в одном испытании равна
в одном испытании равна .
.
Пусть – время ожидания наступления события
– время ожидания наступления события
 раз (за все время ожидания). Найдите
раз (за все время ожидания). Найдите
математическое ожидание
 и дисперсию
и дисперсию .
.
Ti-время ожидания от
(i-1)-ого до i-ого
события
Геометрическое распределение

-
Случайные
величины
 распределены по геометрическому закону
распределены по геометрическому закону
с одинаковым математическим ожиданием,
равным .
.
Найдите математическое ожидание .
.
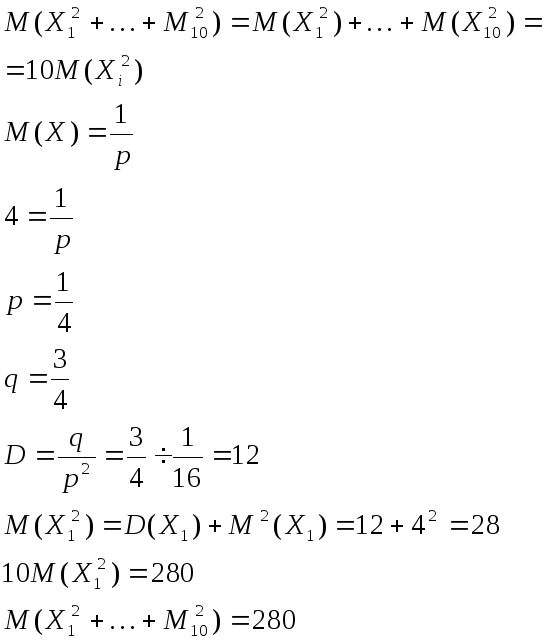
-
Случайные
величины независимы
 и распределены по геометрическому
и распределены по геометрическому
закону с одинаковым математическим
ожиданием, равным .
.
Найдите математическое ожидание .
.

-
Случайные
величины
 распределены по геометрическому закону.
распределены по геометрическому закону.
Найдите дисперсию ,
,
если их математические ожидания равны ,
,
а коэффициент корреляции и
и равен
равен .
.

-
Случайная
составляющая выручки равна
 ,
,
где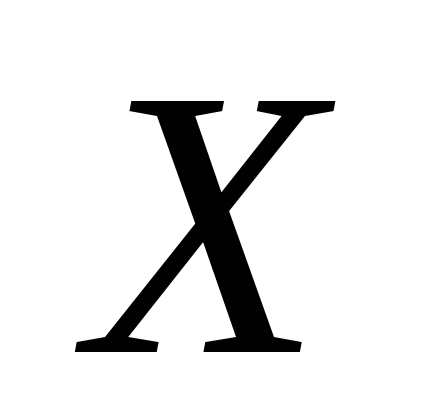 – биномиальная случайная величина с
– биномиальная случайная величина с
параметрами и
и .
.
Случайная составляющая затрат имеет
вид ,
,
где – пуассоновская случайная величина.
– пуассоновская случайная величина.
Найдите дисперсию прибыли, считая, что и
и – независимы, а
– независимы, а .
.

-
Для
пуассоновской случайной величины
 отношение
отношение .
.
Найдите математическое ожидание .
.

● Ковариация
и коэффициент корреляции
-
Даны
математические ожидания случайных
величин
 и
и :
: ,
, ,
,
их дисперсии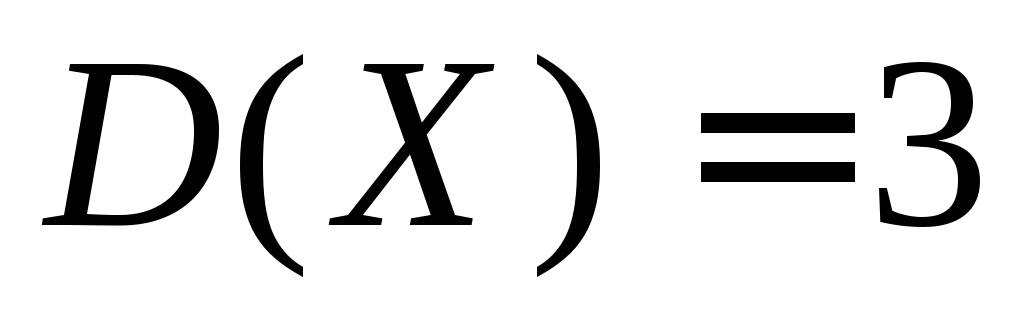 ,
, и ковариация Cov
и ковариация Cov .
.
Найдите математическое ожидание и дисперсию
и дисперсию .
.

-
Случайные
величины
 принимают только значения
принимают только значения и
и .
.
Найдите дисперсию ,
,
если вероятности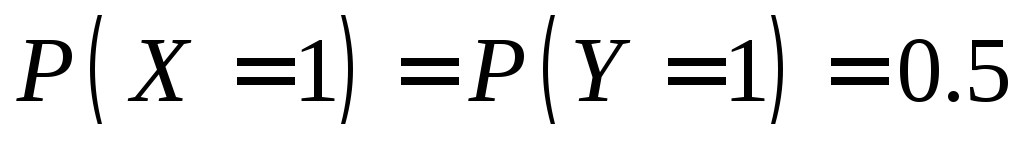 ,
,
а коэффициент корреляции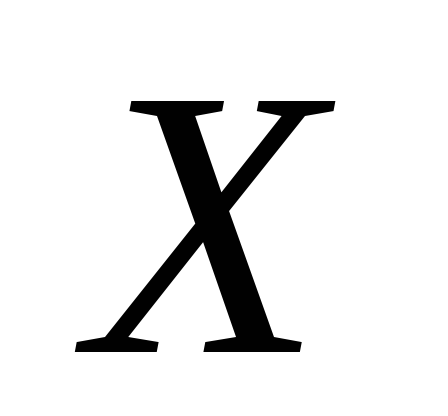 и
и равен
равен .
.
|
X |
1 |
0 |
Y |
1 |
0 |
|
P |
0.5 |
0.5 |
P |
0.5 |
0.5 |

-
Для
случайных величин
 даны их математические ожидания и
даны их математические ожидания и
дисперсии ,
, ,
,
а также коэффициент корреляции .
.
Найдите математическое ожидание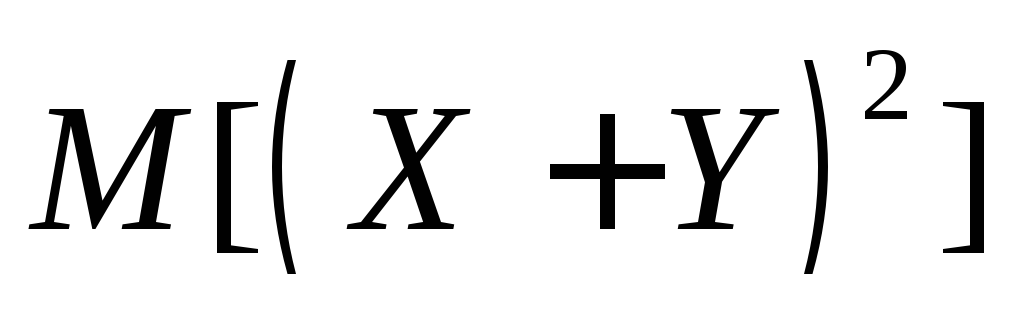 .
.

-
Случайные
величины
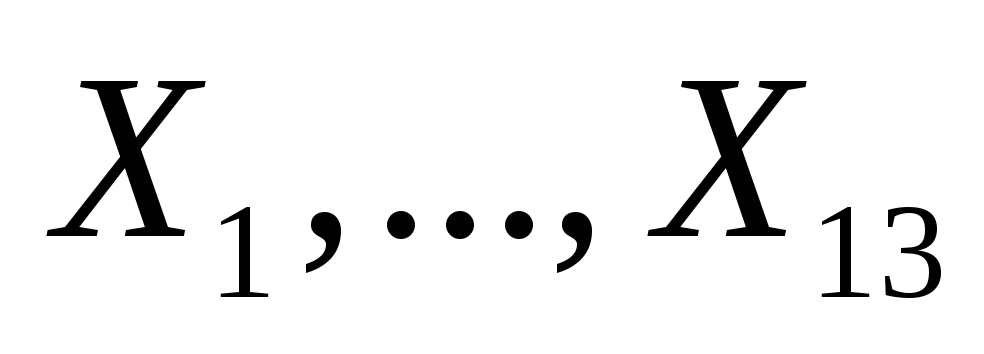 распределены по закону Пуассона с
распределены по закону Пуассона с
одинаковым математическим ожиданием,
равным .
.
Найдите математическое ожидание .
.
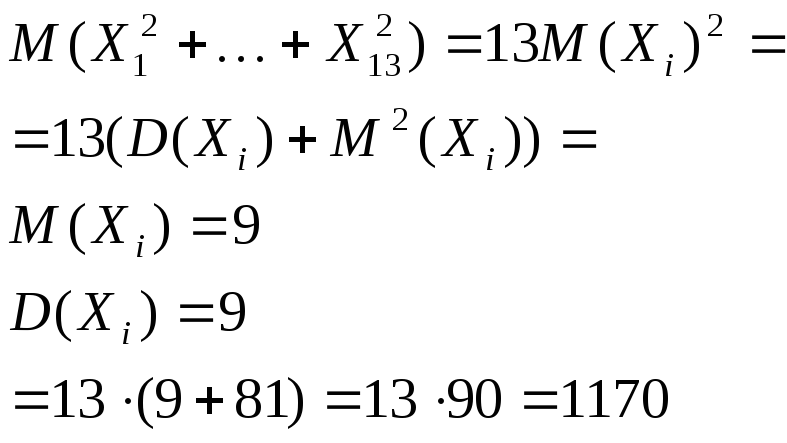
-
Случайные
величины
 независимы и распределены по закону
независимы и распределены по закону
Пуассона с одинаковым математическим
ожиданием, равным .
.
Найдите математическое ожидание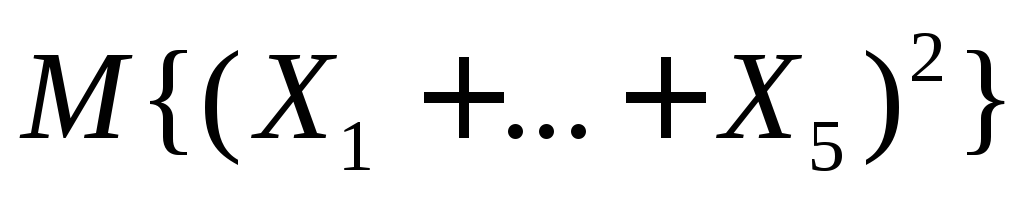 .
.

-
Случайные
величины
 распределены по закону Пуассона. Найдите
распределены по закону Пуассона. Найдите ,
,
если и
и ,
,
а коэффициент корреляции и
и равен
равен .
.

![Решение всех задач по теории вероятности [19.07.18]](https://studrb.ru/files/works_screen/3/51/50.png)
Тема: Решение всех задач по теории вероятности
Раздел: Бесплатные рефераты по теории вероятностей и математической статистике
Тип: Задача | Размер: 715.60K | Скачано: 897 | Добавлен 19.07.18 в 17:21 | Рейтинг: 0 | Еще Задачи
Вуз: Финансовый университет
Решение и остальные задачи смотрите в файле!
Классическая формула сложения вероятностей
1. Независимо друг от друга 5 человек садятся в поезд, содержащий 13 вагонов. Найдите вероятность того, что все они поедут в разных вагонах.
2. В партии из 13 деталей имеется 8 стандартных. Наудачу отобраны 7 деталей. Найдите вероятность того, что среди отобранных деталей ровно 5 стандартных.
3. В киоске продается 9 лотерейных билетов, из которых число выигрышных составляет 3 штуки. Студент купил 4 билета. Какова вероятность того, что число выигрышных среди них будет не меньше 2, но не больше 3?
4. В группе учатся 13 юношей и 9 девушек. Для дежурства случайным образом отобраны три студента. Найдите вероятность того, что все дежурные окажутся юношами.
5. Имеется 25 экзаменационных билетов, на каждом из которых напечатано условие некоторой задачи. В 15 билетах задачи по статистике, а в остальных 10 билетах задачи по теории вероятностей. Трое студентов выбирают наудачу по одному билету. Найдите вероятность того, что хотя бы одному из них не достанется задачи по теории вероятностей.
6. В ящике 3 белых и 4 черных шаров. Найдите вероятность того, что из двух вынутых наудачу шаров один белый, а другой черный. Вынутый шар в урну не возвращается.
7. В ящике 12 шаров, из них 3 белых, а остальные – черные. Из ящика наугад берут 5 шаров. Какова вероятность, что среди выбранных есть хотя бы один белый шар?
Геометрические вероятности
8. В квадрат со стороной 15м случайным образом вбрасывается точка. Найдите вероятность того, что эта точка окажется в правой верхней четверти квадрата или не далее, чем на 2м от центра квадрата.
9. На отрезок длины 240 наудачу поставлена точка . Найдите вероятность того, что меньший из отрезков и имеет длину большую, чем 48.
10. На отрезок длины 120 наудачу поставлена точка . Найдите вероятность того, что меньший из отрезков и имеет длину меньшую, чем 30.
11. На плоскости начерчены две концентрические окружности, радиусы которых 20 и 100 соответственно. Найдите вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в кольцо, образованное построенными окружностями.
12. Внутрь круга радиуса 50 наудачу брошена точка. Какова вероятность того, что точка окажется внутри вписанного в круг квадрата? правильного треугольника? правильного шестиугольника?
13. Двое договорились о встрече между 6 и 7 часами утра, причем договорились ждать друг друга не более 5 минут. Считая, что момент прихода на встречу выбирается каждым наудачу в пределах указанного часа, найти вероятность того, что встреча состоится.
14. В шар радиуса 150 наудачу бросаются 2 точки. Найдите вероятность того, что расстояние от центра шара до ближайшей точки будет не меньше 120.
15. В круг радиуса 150 наудачу бросаются 4 точки. Найдите вероятность того, что расстояние от центра круга до ближайшей точки будет не меньше 75.
16. В шар радиуса 100 наудачу бросаются 4 точки. Найдите вероятность того, что расстояние от центра шара до самой удаленной точки будет не больше 50.
Правила сложения и умножения вероятностей
17. Пусть P(A)=0.88, P(B)=0.55 – вероятности событий. Найдите наименьшую возможную вероятность события AB.
18. Вероятность события P(A)=0.72, P(B)=0.94, P(C)=0.76/ Найдите наименьшую возможную вероятность события ABC.
19. Вероятность хотя бы одного попадания в мишень при 9 выстрелах равна 0.81. Найдите вероятность попадания при одном выстреле.
20. Пассажир подходит к остановке автобусов двух маршрутов. Интервал движения автобусов 1-го маршрута составляет a=19 мин., а 2-го маршрута – B=21 мин. Найдите вероятность того, что пассажир уедет с остановки не позднее, чем через t=6 мин., считая, что его устроит автобус как 1-го, так и 2-го маршрутов.
21. В ящике 8 белых и 13 черных шаров. Два игрока поочередно извлекают по шару, каждый раз возвращая его обратно. Выигрывает тот, кто первым вытащит белый шар. Какова вероятность выигрыша для начинающего игру?
22. Вероятность того, что при одном измерении некоторой физической величины допущена ошибка, равна 0.05. Найдите наименьшее число n измерений, которые необходимо произвести, чтобы с вероятностью P>0.83 можно было ожидать, что хотя бы один результат измерений окажется неверным.
Формула полной вероятности. Формула Байеса
23. В ящике содержатся n1=6 деталей, изготовленных на заводе 1, n2=5 деталей – на заводе 2 и n3=6 деталей – заводе 3. Вероятности изготовления брака на заводах с номерами 1, 2 и 3 соответственно равны p1=0.04, p2=0.02 и p3=0.03. Найдите вероятность p того, что извлеченная наудачу деталь окажется качественной.
24. В урну, содержащую шаров, опущен белый шар, после чего наудачу извлечен один шар. Найдите вероятность того, что извлеченный шар окажется белым, если равновероятны все возможные предположения о первоначальном количестве белых шаров в урне.
25. В первой урне 5 белых и 3 черных шара, во второй – 6 белых и 9 черных. Из второй урны случайным образом перекладывают в первую два шара, после чего из первой урны берут один шар. Какова вероятность того, что этот шар – белый?
26. С первого станка-автомата на сборочный конвейер поступает 18% деталей, со 2-го и 3-го – по 25% и 57% соответственно. Вероятности выдачи бракованных деталей составляют для каждого из них соответственно 0.25%, 0.35% и 0.15%. Найдите вероятность того, что поступившая на сборку деталь окажется бракованной, а также вероятности того, что она изготовлена на 1-м, 2-м и 3-м станках-автоматах, при условии, что она оказалась бракованной.
27. Имеется три одинаковых по виду ящика. В первом ящике 23 белых шара, во втором – 9 белых и 14 черных шаров, в третьем – 23 черных шара. Из выбранного наугад ящика вынули белый шар. Найдите вероятность того, что шар вынут из второго ящика.
28. В среднем из 100 клиентов банка 53 обслуживаются первым операционистом и 47 – вторым. Вероятности того, что клиент будет обслужен без помощи заведующего отделением, только самим операционистом, составляет p1=0.58 и p2=0.88 соответственно для первого и второго служащих банка. Какова вероятность, что клиент, для обслуживания которого потребовалась помощь заведующего, был направлен к первому операционисту?
29. Имеется 13 монет, из которых 3 штуки бракованные: вследствие заводского брака на этих монетах с обеих сторон отчеканен герб. Наугад выбранную монету, не разглядывая, бросают 9 раз, причем при всех бросаниях она ложится гербом вверх. Найдите вероятность того, что была выбрана монета с двумя гербами.
30. Детали, изготовленные в цехе, попадают к одному из 2-х контролёров. Вероятность того, что деталь попадёт к 1-му контролёру, равна 0,8; ко 2-му – 0,2. Вероятность того, что годная деталь будет признана стандартной 1-м контролёром равна 0,96; 2-м контролёром – 0,98. Годная деталь при проверке оказалась стандартной. Найдите вероятность того, что эту деталь проверял 1-й контролёр.
31. Пассажир может обратиться за получением билета в одну из трёх касс (А,B,C). Вероятности обращения в каждую кассу зависят от их местонахождения и равны соответственно 0,4;0,5 и 0,1. Вероятности того, что к моменту прихода пассажира, имеющиеся в кассе билеты распроданы равны соответственно 0,4; 0,3 и 0,1. Найдите вероятность того, что билет куплен. В какой из касс это могло произойти с наибольшей вероятностью?
32. В первой урне m1=7 белых и n1=7 черных шаров, во второй – m2=8 белых и n2=6 черных. Из второй урны случайным образом перекладывают в первую два шара, после чего из первой урны берут один шар, который оказывается белым. Какова вероятность того, что два шара, переложенные из второй урны в первую, были разных цветов?
Схема Бернулли. Числа Pn(k). Наиболее вероятное число успехов
33. Вероятность попадания в цель при одном выстреле равна 0.18. Сделано 7 выстрелов. Найдите вероятность того, что в цель попали менее трех раз.
34. Отрезок длины 6 поделен на две части длины 4 и 2 соответственно, 8 точек последовательно бросают случайным образом на этот отрезок. Найдите вероятность того, что количество точек, попавших на отрезок длины 4 будет больше или меньше 1.
35. Вероятность попадания стрелком в цель равна 1/12. Сделано 132 выстрелов. Определите наивероятнейшее число попаданий в цель.
Схема Бернулли. Приближенные формулы Лапласа и Пуассона
36. Вероятность выпуска бракованного изделия равна 0.4. Найдите вероятность того, что среди 104 выпущенных изделий ровно 62 изделий без брака.
37. Вероятность выпуска бракованного изделия равна p=7/20. Найдите вероятность P того, что среди n=108 выпущенных изделий будет хотя бы одно, но не более s=37 бракованных изделий.
38. Всхожесть семян данного растения равна 90%. Найдите вероятность P того, что из 1200 посаженных семян число проросших семян заключено между 1059 и 1099.
39. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение 1 минуты равна 0.001. Найдите вероятность P того, что в течение одной минуты обрыв произойдет более чем на 2 веретенах.
40. Завод отправил на базу 2000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0.001. Какова вероятность P того, что на базу поступят 3 некачественных изделия?
41. При введении вакцины против полиомиелита иммунитет создается в 99.99% случаях. Определите вероятность того, что из 10000 вакцинированных детей заболеют 1.
2. Дискретные случайные величины
Закон распределения случайной величины
42. Случайная величина X принимает только целые значения 1,2,…,28. При этом вероятности возможных значений X пропорциональны значениям:P(X=k)=ck. Найдите значение константы c и вероятность P(X>2).
43. Случайная величина X принимает только целые неотрицательные значения 0,1,2,…. При этом P(X=k)C*6^-k. Найдите значение константы C и вероятность P(X<3).
Независимые дискретные случайные величины
44. Независимые дискретные случайные величины X,Y принимают только целые значения: X – от 1 до 12 с вероятностью 1/12, – от 1 до 15 с вероятностью 1/15. Найдите вероятность P(X+Y=18).
45. Независимые случайные величины X,Y принимают только целые значения: X – от 1 до 11 с вероятностью 1/11, – от 1 до 9 с вероятностью 1/9. Найдите вероятность P(X
46. Независимые случайные величины X,Y принимают только целые значения: X – от 1 до 10 с вероятностью 1/10, Y – от 1 до 15 с вероятностью 1/15. Найдите вероятность P(X+Y<8)..
47. Независимые случайные величины X,Y принимают только целые значения: X – от -6 до 5 с вероятностью 1/12, – от -6 до 9 с вероятностью 1/16. Найдите вероятность P(XY=0).
48. Независимые случайные величины X и Y принимают только целые значения: X – от -8 до 7, – от -6 до 8. Найдите P(XY>0), если известно, что возможные значения X и Y равновероятны.
49. Независимые случайные величины X,Y принимают только целые значения: X – от -6 до 9 с вероятностью 1/16, Y – от -5 до 8 с вероятностью 1/14. Найдите P(XY<0).
50. Независимые случайные величины X1,…,X8 принимают только целые значения от 0 до 8. Найдите вероятностьP(X1X2…X8=0), если известно, что все возможные значения равновероятны.
51. Независимые случайные величины X,Y,Z принимают только целые значения: X – от 1 до 16 с вероятностью 1/16, Y – от 1 до 12 с вероятностью 1/12, Z – от 1 до 7 с вероятностью 1/7. Найдите вероятность того, что X,Y,Z примут разные значения.
52. Независимые случайные величины X,Y,Z принимают только целые значения: X – от 1 до 13 с вероятностью 1/13, Y – от 1 до 9 с вероятностью 1/9, Z – от 1 до 7 с вероятностью 1/7. Найдите вероятность P(X < Y < Z)
Математическое ожидание и дисперсия дискретной случайной величины
53. Распределение дискретной случайной величины задано таблицей
54. Дискретная случайная величина X принимает только целые значения 1,4,7,10,13, каждое с вероятностью 1/5. Найдите математическое ожидание m=M(X) и вероятность P(X
55. Распределение дискретной случайной величины задано таблицей
Найдите дисперсию D(X).
56. Распределение случайной величины X задано таблицей
|
X |
4 |
8 |
11 |
14 |
18 |
|
P |
0.1 |
0.25 |
0.3 |
0.25 |
0.1 |
Найдите математическое ожидание m=M(X), среднее квадратичное отклонение 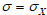 и вероятность
и вероятность 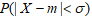
57. Для случайной величины X известно, что 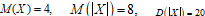 . Найдите дисперсию D(X).
. Найдите дисперсию D(X).
58. Независимые дискретные случайные величины X,Y могут принимать только значения 0 и 1. При этом P(X=0)=0.1, P(X=0)=0.9. Найдите математическое ожидание M[(X+Y)^2].
|
X |
0 |
1 |
Y |
0 |
1 |
|
P |
0.1 |
0.9 |
P |
0.9 |
0.1 |
59. Независимые дискретные случайные величины X,Y могут принимать только значения 0 и 1. При этом P(X=0)=0.1, P(X=0)=0.6. Найдите математическое ожидание M[(X-Y)^2].
|
X |
0 |
1 |
Y |
0 |
1 |
|
P |
0.1 |
0.9 |
P |
0.6 |
0.4 |
60. Дискретные случайные величины X1,X2,…,X9 распределены по закону, заданному таблицей
Найдите математическое ожидание 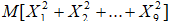
61. Независимые случайные величины X1,X2,…,X8 принимают только целые значения -9,-8,…,12,13. Найдите математическое ожидание M(X1X2…X8), если известно, что возможные значения равновероятны.
62. Для независимых случайных величин X1,…,X4 известно, что их математические ожидания M(Xi)=-1, дисперсии D(Xi)=1, i=1,…,4. Найдите дисперсию произведения D(X1…X4).
63. Независимые случайные величины X1,…,X60 могут принимать только значения 0 и 1. При этом P(Xi=0)=0.9, i=1,…,60. Найдите математическое ожидание 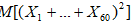 .
.
64. Независимые случайные величины X1,…,X3 могут принимать только значения 0 и 1. При этом P(Xi=0)=0.4, i=1,…,3. Найдите математическое ожидание 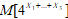 .
.
65. Вероятность выигрыша 3 рублей в одной партии равна 2/5, вероятность проигрыша 2 рублей равна 3/5. Найдите дисперсию капитала игрока после 5 партий.
Основные дискретные законы распределения и их характеристики
66. На плоскости начерчены две окружности, радиусы которых 5 и 25 соответственно. Меньшая окружность содержится внутри большего круга. В большой круг наудачу бросают 5 точек. Пусть случайная величина X – число точек, попавших в малый круг. Вычислите математическое ожидание M(X) и дисперсию D(X).
67. Производится 1920 независимых испытаний, состоящих в том, что одновременно подбрасываются 7 монет. Пусть X – число испытаний, в которых выпало 3 герба. Найдите математическое ожидание M(X)
68. Случайные величины X1,…,X192 распределены по биномиальному закону с параметрами n=4 и p=5/8. Найдите математическое ожидание
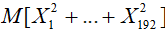
69. Случайные величины X1,…,X27 независимы и распределены по биномиальному закону с параметрами n=5 и p=2/3. Найдите математическое ожидание
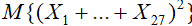
70. Отрезок длины поделен на две части длины 25 и 10 соответственно. Наудачу 6 точек последовательно бросают на отрезок. X – случайная величина, равная числу точек, попавших на отрезок длины 10. Найдите математическое ожидание и среднее квадратичное отклонение величины X.
71. Производится 14 независимых испытаний, в каждом из которых подбрасываются игральные кости. Пусть X – число испытаний, в которых все выпавшие цифры оказались >2. Найдите дисперсию D(X).
72. Производится 10 независимых испытаний с вероятностью успеха 0.6 в каждом испытании. Пусть X – число успехов в испытаниях с номерами 1,2,…,7, Y – число успехов в испытаниях с номерами 5,6,…,10. Найдите дисперсию D[X+2Y].
73. На плоскости начерчены два квадрата, стороны которых 20 и 40 соответственно. Меньший квадрат содержится внутри большего квадрата. В большой квадрат случайным образом бросают точки до тех пор, пока не попадут в маленький квадрат. Пусть случайная величина X – число бросаний. Найдите математическое ожидание M(X) и дисперсию D(X).
74. В спортивной лотерее каждую неделю на 100 билетов разыгрывается палаток и рюкзаков. Турист решил каждую неделю покупать по одному билету до тех пор, пока он не выиграет палатку и рюкзак. Найдите среднее время реализации данного намерения (время измеряется в неделях).
75. В серии независимых испытаний, которые проводятся с частотой одно испытание в единицу времени, вероятность наступления события в одном испытании равна 1/4. Пусть T – время ожидания наступления события A 10 раз (за все время ожидания). Найдите математическое ожидание M(T) и дисперсию D(T).
Случайные величины X1,…,X10 распределены по геометрическому закону с одинаковым математическим ожиданием, равным 4. Найдите математическое ожидание.
76. Случайные величины независимы X1,…,X8 и распределены по геометрическому закону с одинаковым математическим ожиданием, равным 6. Найдите математическое ожидание
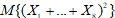
77. Случайные величины X,Y распределены по геометрическому закону. Найдите дисперсию D[X-Y], если их математические ожидания равны 4, а коэффициент корреляции X и Y равен 0.5.
78. Случайная составляющая выручки равна 4X, где X – биномиальная случайная величина с параметрами n=500 и p=1/2. Случайная составляющая затрат имеет вид 50Y, где Y – пуассоновская случайная величина. Найдите дисперсию прибыли, считая, что X и Y – независимы, а M(Y)=5.
79. Для пуассоновской случайной величины X отношение 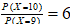 . Найдите математическое ожидание M[X].
. Найдите математическое ожидание M[X].
Решение и остальные задачи смотрите в файле!
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Бесплатная оценка
0
19.07.18 в 17:21
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Добавить работу
Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
На этой странице вы узнаете
- Как кот может быть одновременно жив и мертв?
- Можно ли всегда выигрывать спор с монеткой?
- Если рандомно ответить на вопрос теста, какой шанс угадать ответ?
Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.
Вероятность
Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…
Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться.
Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов.
Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат.
Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом.
По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив.
Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным. Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв.
Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:
- выпадет орел;
- выпадет решка.

Эти два события образуют множество элементарных событий.
Множество элементарных событий — множество всех возможных результатов случайного эксперимента.
В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации.
Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран.
Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности.
Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу.
(P = frac{m}{n})
Вероятность можно обозначить, как P(x), где х — некоторое событие.
Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.
Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.
Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна (P = frac{2}{2} = 1), то есть мы точно выиграем спор.
Однако вероятность не так проста, и даже здесь подготовила ловушку.
В редких случаях есть и третий вариант событий — монетка встанет на ребро. Вероятность такого события составляет (frac{1}{6000}). То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет.
Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%.
Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?
Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна
(frac{49}{140} = 0,35)
Выразим в процентах:
0,35 * 100% = 35%
Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ.
Ответ: 0,35
Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой.
(P = frac{m}{n} * 100%)
Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.
Равновозможные и противоположные события
Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными.
Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие.
Вероятности появления событий равны.
Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий.
Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них.
В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий.
Мы подбросили монету и выпал орел. Следовательно, не выпала решка.
А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными.
Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как (overline{A}).
Заметим, что вероятность события A равняется 12, как и вероятность события (overline{A}). Чему равна их сумма?
)frac{1}{2} + frac{1}{2} = 1)
Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1.
(P(A) + P(overline{A}) = 1)
Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить.
Объединение и пересечение событий
Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим?
Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий.
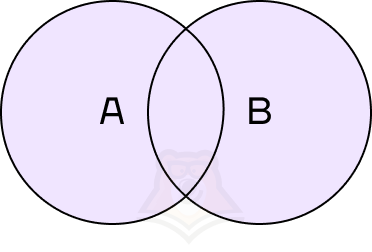
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег.
Объединение событий обозначается знаком (cup). Объединение событий А и В можно записать как (A cup B).
Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?
Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям.

Пересечение событий обозначается знаком (cap). Пересечение событий А и В можно записать как (A cap B).
Несовместные и совместные события
Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.
Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно.
Несовместные события — такие события, появление одного из которых исключает появление другого.
Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности.

Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.
Сформулируем определение суммы вероятностей двух несовместных событий.
Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:
(P(A cup B) = P(A) + P(B))
Если существуют несовместные события, то существуют и совместные.
Совместные события — события, наступление одного из которых не исключает наступления другого.
В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят? Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет.
Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”.
Найдем вероятность события А: (frac{1}{6}).
Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна (frac{3}{6} = frac{1}{2})
Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А.
Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги.

А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок.
Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:
(P(A cup B) = P(A) + P(B) — P(A cap B))
В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике.
Независимые и зависимые события
Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем.
Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна (frac{95}{100} = 0,95).
Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?
Ответим на вопрос: зависят ли булочки друг от друга?
Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми.
Независимые события — такие события, появление одного из которых не зависит от появления другого события.
Определим вероятность независимых событий.
Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95.
А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:
(P(A cap B) = P(A) * P(B))
Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025.
В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”.
Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой.
Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого.
Но если автоматы стоят рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого.
Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?

Нужная последовательность может быть в двух случаях:
- сначала вытащат фиолетовый кубик и потом снова фиолетовый;
- сначала вытащат оранжевый кубик, а потом фиолетовый.
Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна (frac{5}{7}). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые.

Вероятность вытащить во второй раз фиолетовый кубик равна (frac{5}{7} * frac{4}{6} = frac{20}{42} = frac{10}{21}).

Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна (frac{2}{7}). В мешке останется шесть кубиков, пять из которых будут фиолетовыми.

Вероятность вытащить во второй раз фиолетовый кубик будет уже равна (frac{2}{7} * frac{5}{6} = frac{10}{42} = frac{5}{21}).
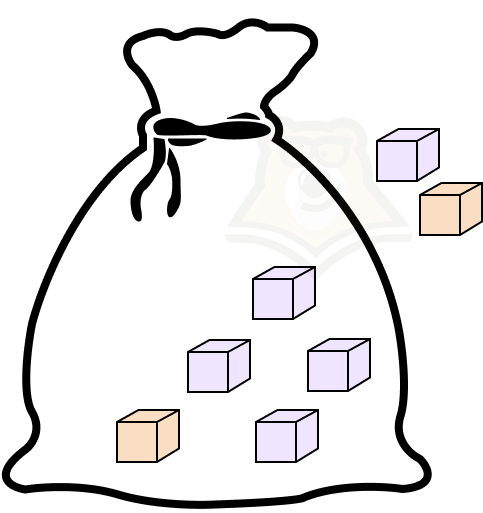
В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы.
Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.
Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.
Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность.
Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:
(P(A cap B) = P(A) * P(B | A))
Формула Бернулли
Рассмотрим случаи, когда испытание повторяется многократно. Для этого еще раз обратимся к игральному кубику. Подбросим кубик 8 раз. Какова вероятность, что цифра 5 выпала ровно три раза?
Пусть p — вероятность, что выпадет цифра 5. Тогда (p = frac{1}{6}).
Теперь возьмем q — противоположное р событие — вероятность, что цифра 5 не выпадет. (q = frac{5}{6}).
Обозначим количество всех бросков за n, а количество выпадения цифры 5 за k.
Чтобы решить задачу, нужно воспользоваться формулой Бернулли.
(P_n(k) = C_n^k * p^k * q^{n — k})
Множитель (C_n^k) — это число сочетаний. Подробнее узнать про сочетания можно в статье «Основы комбинаторики».
Решим задачу, подставив значения в формулу:
(P_8(3) = C_8^3 * (frac{1}{6})^3 * (frac{5}{6})^5 = frac{8!}{5!3!} * frac{1}{6^3} * frac{5^5}{6^5} = frac{6 * 7 * 8}{1 * 2 * 3} * frac{5^5}{6^8} approx 0,1)
Фактчек
- Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
- События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
- События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A (cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A cup B) = P(A) + P(B) — P(A cap B).
- События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A cap B) = P(A) * P(B | A).
- Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Проверь себя
Задание 1.
Какие события являются несовместными?
- Подбрасывание монетки.
- Брак батареек в одной упаковке.
- “Миша идет” и “Миша стоит”.
- Случайное вытаскивание конфет из вазы.
Задание 2.
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?
- 0,17
- 1
- 0,83
- 1,17
Задание 3.
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?
- 1
- 0,216
- 0,45
- 1,5
Задание 4.
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут.
- 0,3
- 0,001
- 2,7
- 0,729
Задание 5.
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой.
- 0,77
- 0,135
- 0,23
- -0,23
Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1
