Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
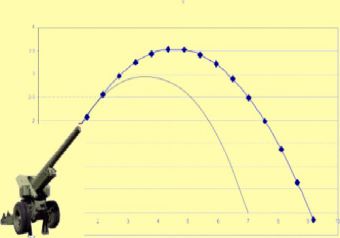
Важные факты!График движения тела, брошенного под углом к горизонту:

α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
- Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
vmin = v0 cosα = vh
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
vmax = vo = v
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:

Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0x tполн = v0 cosα tполн
Подставляя в выражение формулу полного времени полета, получаем:

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
x = v0 cosα t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:

Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:

Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
v0 sinα = gtпод
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:

Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
Важные факты!
График движения тела, брошенного под углом к горизонту с некоторой высоты:

Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
tполн = tпад + tпод
Уравнение координаты x:
x = v0 cosα t
Уравнение координаты y:

Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Задание EF17562
С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.
Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22
Отсюда высота H равна:
H=mgl1mg+mv22mg=l1+v22g
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2β2g=v2sin2(90−2α)o2g
Отсюда:
l1=h−v2sin2(90−2α)o2g
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g
H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)
H=1,4−10·0,422(sin2(90−60)o−1)
H=1,4−5·0,16(sin230o−1)
H=1,4−0,8((12)2−1)=1,4−0,8(14−1)
H=1,4+0,6=2 (м)
Ответ: 20
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17980
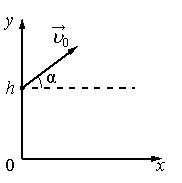
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

Алгоритм решения
- Установить вид механического движения, исходя из условий задачи.
- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:

Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:

Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:

В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
![]()
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:

Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
Ответ: 42
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 42.9k
1. Определить, на какой высоте находится тело, в любой точке траектории движения
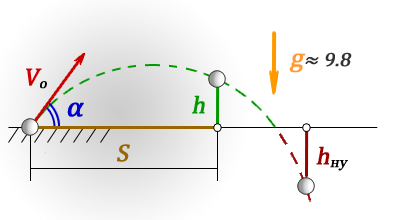
h – высота тела в момент времени t
hну – высота ниже уровня броска (принимает отрицательное значение)
S – дальность полета по горизонтали
t – время полета
Vo – начальная скорость тела
α – угол под которым брошено тело
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула для определения значения высоты тела в момент времени t
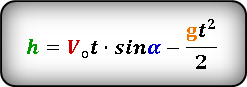
Формула для определения значения высоты тела через расстояние S по горизонтали
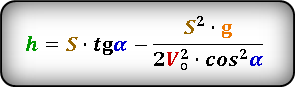
hну – высота ниже уровня броска, принимает отрицательное значение
2. Найти максимальную высоту, на которую поднялось тело
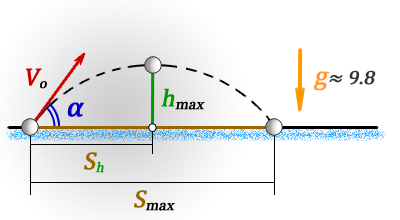
hmax – максимальная высота
Smax – максимальная дальность полета, если бросок и падение на одном уровне
Sh – расстояние пройденное по горизонтали до момента максимального подъема
tmax – время всего полета
th – время за которое тело поднялось на максимальную высоту
Vo – начальная скорость тела
α – угол под которым брошено тело
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула для расчета максимальной высоты достигнутое телом, если даны, начальная скорость Vo и угол α под которым брошено тело. :
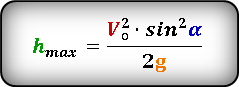
Формула для вычисления максимальной высоты, если известны, максимальное расстояние S max или расстояние по горизонтали при максимальной высоте Sh и угол α под которым брошено тело. :
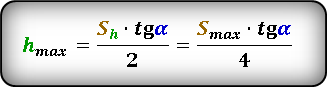
По этой формуле, можно определить максимальную высоту, если известно время th за которое тело поднялось на эту высоту. :
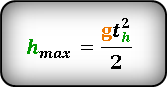
- Подробности
-
Опубликовано: 11 августа 2015
-
Обновлено: 13 августа 2021
Обновлено: 14.05.2023
Если тело бросить вертикально вверх при наличии начальной скорости υ 0 , оно будет двигаться равнозамедленно с ускорением, равным a = – g = – 9 , 81 υ c 2 .

Формулы вычисления показателей движения брошенного тела
Высота подбрасывания h за время t и скорость υ через промежуток t можно определить формулами:
t m a x – это время, за которое тело достигает максимальной высоты h m a x = h , при υ = 0 , а сама высота h m a x может быть определена при помощи формул:
Когда тело достигает высоты, равной h m a x , то оно обладает скоростью υ = 0 и ускорением g . Отсюда следует, что тело не сможет оставаться на этой высоте, поэтому перейдет в состояние свободного падения. То есть, брошенное вверх тело – это равнозамедленное движение, при котором после достижения h m a x изменяются знаки перемещения на противоположные. Важно знать, какая была начальная высота движения h 0 . Общее время тела примет обозначение t , время свободного падения – t п , конечная скорость υ к , отсюда получаем:
Если тело брошено вертикально вверх от уровня земли, то h 0 = 0 .
Время, необходимое для падения тела с высоты, куда предварительно было брошено тело, равняется времени его подъема на максимальную высоту.
Так как в высшей точке скорость равняется нулю видно:
Конечная скорость υ к тела, брошенного от уровня земли вертикально вверх, равна начальной скорости υ 0 по величине и противоположна по направлению, как показано на ниже приведенном графике.

Примеры решения задач
Тело было брошено вертикально вверх с высоты 25 метров со скоростью 15 м / с . Через какой промежуток времени оно достигнет земли?
Дано: υ 0 = 15 м / с , h 0 = 25 м , g = 9 , 8 м / с 2 .
Найти: t .
Решение
t = υ 0 + υ 0 2 + g h 0 g = 15 + 15 2 + 9 , 8 · 25 9 , 8 = 3 , 74 с
Ответ: t = 3 , 74 с .
Был брошен камень с высоты h = 4 вертикально вверх. Его начальная скорость равняется υ 0 = 10 м / с . Найти высоту, на которую сможет максимально подняться камень, его время полета и скорость, с которой достигнет поверхности земли, пройденный телом путь.
Дано: υ 0 = 10 м / с , h = 4 м , g = 9 , 8 м / с 2 .
Найти: H , t , v 2 , s .
Решение

H = h 0 υ 0 2 2 g = 4 + 10 2 9 , 8 = 14 , 2 м .
t = υ 0 + υ 0 2 + g h 0 g = 10 + 10 2 + 9 , 8 · 4 9 , 8 = 1 , 61 с .
υ 2 = υ k = 2 g H = 2 · 9 , 8 · 14 , 2 = 16 , 68 м / с .
s = H – h 0 + H = 2 H – h 0 = 2 · 14 , 2 = 24 , 4 м .
Ответ: H = 14 , 2 м ; t = 1 , 61 с ; v 2 = 16 , 68 м / с ; s = 24 , 4 м .
Согласно второму закону Ньютона, сила тяжести, обусловленная гравитационным притяжением, действует на все тела на поверхности Земли и вблизи неё вне зависимости от того, покоятся они или движутся.
При свободном падении тело движется равноускоренно. Это значит, что скорость свободно падающего тела увеличивается при приближении к поверхности Земли. Этому способствует ускорение свободного падения (рис. (1)).

Если подбросить тело вверх, то при отсутствии сопротивления воздуха, тело будет двигаться только под действием силы тяжести (рис. (2)), которая направлена вниз (к центру Земли). В эту же сторону направлено и ускорение свободного падения.

Чем большую начальную скорость получило тело при броске, тем больше будет время подъёма, и тем на большую высоту оно поднимется к моменту остановки.
После того как тело поднялось на наибольшую высоту, оно под действием силы тяжести начинает равноускоренно падать вниз.
Вдоль оси (Oy) тело движется равноускоренно с ускорением свободного падения g y и начальной скоростью υ 0 .
При движении вверх с начальной скоростью υ 0 значение скорости будет уменьшаться, тело будет замедляться. Направления проекций скорости и ускорения свободного падения на ось (Oy) будут противоположными.
При броске тела вверх оно замедляется с ускорением g≈9,8 м/с², обусловленным гравитационным притяжением Земли. Именно поэтому в некоторый момент времени подброшенное тело останавливается и начинает движение в обратном направлении, вниз. Расстояние от точки смены направления движения тела до поверхности Земли и будет равно максимальной высоте подъема.
- Как найти максимальную высоту подъема
- Как рассчитать скорость падения
- Как найти время падения тела
- – секундомер;
- – радар;
- – калькулятор;
- – угломер.
Найдите максимальную высоту подъема тела, брошено вверх при помощи секундомера. Не имеет значения, брошено ли тело вертикально вверх или под углом к горизонту. При помощи секундомера, засеките время, которое тело находилось в полете. Измеряйте значение времени в секундах. Поскольку половину времени, проведенного в полете тело поднимается, во вторую половину опускается, полученное значение поделите на 2.
Рассчитайте максимальную высоту подъема тела Н. Для этого возведите поделенное на 2 время полета t в квадрат. Полученное значение умножьте на ускорение свободного падения g≈9,8 м/с², а результат поделите на число 2, H=g∙t²/2. Высоту получите в метрах.
Пример. После броска с поверхности Земли тело снова упало на нее через 4 с, на какую максимальную высоту оно поднялось? Найдите время подъема тела на максимальную высоту. Оно равно половине всего времени движения 4/2=2 с. Подставьте значение в формулу H=g∙t²/2=9,8∙2²/2≈20 м. Если не требуется повышенная точность, значение ускорения свободного падения можно брать 10 м/с².
Определите максимальную высоту подъема тела, если известна его начальная скорость. Ее можно измерить специальным радаром. В некоторых устройствах, она изначально известна. В том случае, если тело запущено вертикально вверх с начальной скоростью v0, чтобы найти максимальную высоту подъема этого тела поделите квадрат этой начальной скорости на удвоенное значение ускорения свободного падения, H=v0²/2∙g. Скорость должна быть измерена в метрах в секунду.
Найдите максимальную высоту подъема тела, начальная скорость v0 которого направлена под углом к горизонту. При расчете учитывайте, что за подъем тела отвечает только вертикальная составляющая скорости, которая равна v0y= v0∙sin(α), где α – угол к горизонту, под которым тело начало свое движение, его измерьте угломером. Тогда для расчета максимальной высоты подъема тела можно использовать формулу, описанную в предыдущем пункте, а получившийся результат умножит на синус α, возведенный в квадрат H=(v0²/2∙g)∙sin²(α).
На какую высоту поднимется тело, брошенное вертикально вверх с начальной скоростью 800 м/с. Сопротивлением воздуха пренебречь.
Решение задачи:

Первый способ решения – длинный.
Тело бросают вертикально вверх с начальной скоростью, из-за ускорения свободного падения оно равно или поздно достигнет максимально высоты, остановится и устремится обратно к земле. Для того, чтобы определить эту высоту запишем уравнения движения и уравнение скорости тела:
В точке максимального подъема скорость тела (upsilon) равна нулю. Из выражения (2) определим время полета:
[upsilon = 0 Rightarrow 0 = <upsilon _0>– gt Rightarrow t = frac<<<upsilon _0>>>]
Подставим полученную формулу в выражение (1):
Второй способ решения – короткий.
Используем известную формулу без времени (знак “минус” справа присутствует из-за того, что движение замедленное!):
Конечная скорость (upsilon) равна нулю, поэтому формула станет короче. Выразим оттуда искомую высоту (h).
[upsilon _0^2 = 2gh Rightarrow h = frac<<upsilon _0^2>>>]
Видно, что если в задаче не дано времени, то лучше использовать второй способ.
Ответ: 32 км.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
помогите пожалуйста решить задачи:
1) Определите на какую максимальную высоту поднимется тело, если его подбросили вертикально вверх со скоростью 30 м/с.
2) Определите скорость пули через 2,5 с после выстрела вертикально вверх, если скорость в момент вылета из ствола была 300 м/с.
1) Используем формулу кинематики без времени: [ <upsilon ^2>– upsilon _0^2 = – 2gH]На максимальной высоте скорость тела будет равна нулю, тогда:[upsilon _0^2 = 2gH]Максимальная высота равна:[H = frac<<upsilon _0^2>>>][H = frac^2>>>> = 45;м]
2) Скорость пули в любой момент, движущейся вертикально вверх, можно найти по формуле:[upsilon = <upsilon _0>– gt][upsilon = 300 – 10 cdot 2,5 = 275;м/с]

Спасибо за ответ я понял как теперь решать
Можете сказать название формулы, использованной в первом шаге второго способа?υ
v2—v02=—2gh

По сути это закон сохранения энергии Ещё называют формулой кинематики без времени
Я взял формулу h_max = v_0^2*sin^2a/2*g a = 90. У меня вышло тот же самый ответ только, боюсь что я взял не правильную формулу. Или нет?

Да, Вы взяли формулу максимальной высоты для тела, брошенного под углом к горизонту, а в задаче тело брошено вертикально вверх. Правильная формула показана в решении выше (как и вывод этой формулы).
у меня вместо формул что-то вроде ^2>>>><<<<562<>[]
Для корректного отображения формул на сайте в браузере должны быть разрешены запуски скриптов js
С какой максимальной скоростью человек может бросить камень или мячик своей рукой?
Для решения задачи используем информацию о рекордной скорости бейсбольного мяча на подаче, равный v ≈ 45 м/сек. Масса бейсбольного мяча известна и приближенно равна m = 0,145 кг. Соответствующую кинетическую энергию (Е), затраченную на бросок мяча рукой, оценим из формулы Е ≈ (δМ + m)v²/2, где М — масса человека, а δМ = 0,005М — масса кисти руки.
Подставив в формулу массу среднего человека, M ≈ 70 кг, получим, что энергия рекордного броска равнялась E ≈ 500 Дж. Зафиксировав это значение как предел, решим теперь задачу в обратном направлении — найдём приближённую формулу для максимальной скорости (v) произвольного предмета с массой m, брошенного человеком с массой М, при фиксированной максимальной энергии E = 500 Дж.
Ответ: v ≈ √ ≈ √, [м/сек], где m и М в единицах кг. Подставив числовые значения, определим скорость,с которой человек может кинуть бейсбольный мяч. V= √1000/0.005×70+0.145=45 м/с=162км/ч
Можно сказать,что проверили информацию о рекордной скорости бейсбольного мяча на подаче, равный v ≈ 45 м/сек.
В газете прочитал такую статью: “Насколько высоко человек может что-либо подбросить?. Возьмем,например, бейсбольный мяч.Питчер, кидающий фастбол на скорости 130 км/, сумеет добросить его до высоты 50 метров. Я решил взять вышеуказанную задачу и проверить результат в 50 метров. Перевел в м/с: 130 км/час=36м/с
Выбрав вторую формулу, находим h=36^2/2×10=64.8 метра.
Правильно я проверил?
Думаю, да.
Проблема в том, что питчер не кидает мяч вертикально вверх, а формула справедлива только для мяча, брошенного вертикально вверх.
У меня получилось вот так:
Уравнение движения тела y = v_0 * t – (g * t^2 )/2. (*)
Время t можно найти из этого уравнения g = (v – v_0)/t => t = (v – v_0)/g. t = 81,6c
Подставим все известные значения в уравнение (*) и получим y = 32653 м.
Разница между вашими моим ответом 653 м.
В решении я принял, что (g = 10;м/с^2), а у Вас по всей видимости (g = 9,81;м/с^2). Разница в 600 с лишним метров в таком случае нормальна. Это всего лишь 2% от 32000 м.
Ваше решение тоже правильно (как и моё), хотя мне не нравится один момент. Вы решает по действиям и накапливаете ошибку. Если использовать мою конечную формулу и принять (g = 9,81;м/с^2), то:
[h = frac^2>>>> = 32619,8;м]
Тогда у нас с Вами разница 40 м, а её вообще не должно быть.
Читайте также:
- Что такое потолок кратко
- Кластер что это в экономике кратко и понятно
- Модели здоровьесберегающей деятельности школы типичная недостаточная
- Что рассказывается о повести временных лет о начале руси кратко
- Комплексный анализ текста 2 класс школа россии
Движение тела, брошенного под углом к горизонту, теория и онлайн калькуляторы
Движение тела, брошенного под углом к горизонту
Начальные условия. Движение тела, брошенного под углом к горизонту
Рассмотрим движение тела в поле тяжести Земли, сопротивление воздуха учитывать не будем. Пусть начальная скорость брошенного тела направлена под углом к горизонту $alpha $ (рис.1). Тело брошено с высоты ${y=h}_0$; $x_0=0$.
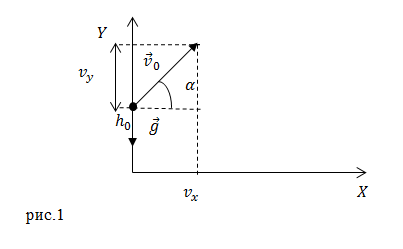
Тогда в начальный момент времени тело имеет горизонтальную ($v_x$) и вертикальную ($v_y$) составляющие скорости. Проекции скорости на оси координат при $t=0$ равны:
[left{ begin{array}{c}
v_{0x}=v_0{cos alpha , } \
v_{0y}=v_0{sin alpha . } end{array}
right.left(1right).]
Ускорение тела равно ускорению свободного паления и все время направлено вниз:
[overline{a}=overline{g}left(2right).]
Значит, проекция ускорения на ось X равна нулю, а на ось Y равна $a_y=g.$
Так как по оси X составляющая ускорения равна нулю, то скорость движения тела в этом направлении является постоянной величиной и равна проекции начальной скорости на ось X (см.(1)). Движение тела по оси X равномерное.
При ситуации, изображенной на рис.1 тело по оси Y будет двигаться сначала вверх, а затем виз. При этом ускорение движения тела в обоих случаях равно ускорению $overline{g}.$ На прохождение пути вверх от произвольной высоты ${y=h}_0$ до максимальной высоты подъема ($h$) тело тратит столько же времени, сколько на падение вниз от $h$ до ${y=h}_0$. Следовательно, точки симметричные относительно вершины подъема тела лежат на одинаковой высоте. Получается, что траектория движения тела симметрична относительно точки-вершины подъема – и это парабола.
Скорость движения тела, брошенного под углом к горизонту можно выразить формулой:
[overline{v}left(tright)={overline{v}}_0+overline{g}t left(3right),]
где ${overline{v}}_0$ – скорость тела в момент броска. Формулу (3) можно рассматривать как результат сложения скоростей двух независимых движений по прямым линиям, в которых участвует тело.
Выражения для проекции скорости на оси принимают вид:
[left{ begin{array}{c}
v_x=v_0{cos alpha , } \
v_y=v_0{sin alpha -gt } end{array}
left(4right).right.]
Уравнение для перемещения тела при движении в поле тяжести:
[overline{s}left(tright)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(5right),]
где ${overline{s}}_0$ – смещение тела в начальный момент времени.
Проектируя уравнение (5) на оси координат X и Y, получим:
[left{ begin{array}{c}
x=v_0{cos left(alpha right)cdot t, } \
y={h_0+v}_0{sin left(alpha right)cdot t-frac{gt^2}{2} } end{array}
left(6right).right.]
Тело, двигаясь вверх, имеет по оси Y сначала равнозамедленное перемещение, после того, как тело достигает вершины, движение по оси Y становится равноускоренным.
Траектория движения материальной точки получается, задана уравнением:
[y=h+x tg alpha -frac{gx^2}{2v^2_0{cos}^2alpha }left(7right).]
По форме уравнения (7) видно, что траекторией движения является парабола.
Время подъема и полета тела, брошенного под углом к горизонту
Время, затрачиваемое телом для того, чтобы достигнуть максимальной высоты подъема получают из системы уравнений (4). . В вершине траектории тело имеет только горизонтальную составляющую, $v_y=0.$ Время подъема ($t_p$) равно:
[t_p=frac{v_0{sin alpha }}{g}left(8right).]
Общее время движения тела (время полета ($t_{pol}))$находим из второго уравнения системы (6), зная, что при падении тела на Землю $y=0$, имеем:
[t_{pol}=frac{v_0{sin alpha +sqrt{v^2_0{sin}^2alpha +2gh} }}{g}left(9right).]
Дальность полета и высота подъема тела, брошенного под углом к горизонту
Для нахождения горизонтальной дальности полета тела ($s$) при заданных нами условиях в уравнение координаты $x$ системы уравнений (6) следует подставить время полета ($t_{pol}$) (9). При $h=0,$ дальность полета равна:
[s=frac{v^2_0{sin left(2alpha right) }}{g}left(10right).]
Из выражения (9) следует, что при заданной скорости бросания дальность полета максимальна при $alpha =frac{pi }{4}$.
Максимальную высоту подъема тела ($h_{max}$) находят из второго уравнения системы (6), подставляя в него время подъема ($t_p$) (8):
[h_{max}=h+frac{{v_0}^2{{sin}^2 б }}{2g}left(11right).]
Выражение (11) показывает, что максимальная высота подъема тела прямо пропорциональна квадрату скорости бросания и увеличивается при росте угла бросания.
Примеры задач с решением
Пример 1
Задание. Во сколько раз изменится время полета тела, которое бросили с высоты $h$ в горизонтальном направлении, если скорость бросания тела увеличили в $n$ раз?
Решение. Найдем формулу для вычисления времени полета тела, если его бросили горизонтально (рис.2).
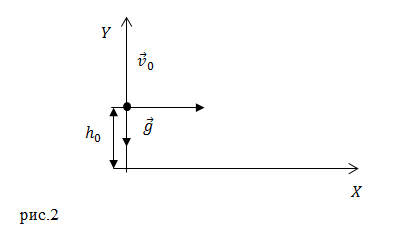
В качестве основы для решения задачи используем выражение для равноускоренного движения тела в поле тяжести:
[overline{s}={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(1.1right).]
Используя рис.2 запишем проекции уравнения (1.1) на оси координат:
[left{ begin{array}{c}
X:x=v_0t;; \
Y:y=h_0-frac{gt^2}{2} end{array}
right.left(1.2right).]
Во время падения тела на землю $y=0,$ используем этот факт и выразим время полета из второго уравнения системы (1.2), имеем:
[0=h_0-frac{g{t_{pol}}^2}{2}to t_{pol}=sqrt{frac{2h_0}{g}} left(1.3right).]
Как мы видим, время полета тела не зависит от его начальной скорости, следовательно, при увеличении начальной скорости в $n$ раз время полета тела не изменится.
Ответ. Не изменится.
Пример 2
Задание. Как изменится дальность полета тела в предыдущей задаче, если начальную скорость увеличить в $n$ раз?
Решение. Дальность полета – это расстояние, которое пройдет тело по горизонтальной оси. Это означает, что нам потребуется уравнение:
[x=v_0t (2.1)]
из системы (1.2) первого примера. Подставив вместо $t,$ время полета, найденное в (1.3), мы получим дальность полета ($s_{pol}$):
[s_{pol}=v_0t_{pol}=v_0sqrt{frac{2h_0}{g}} left(2.2right).]
Из формулы (2.2) мы видит, что при заданных условиях движения дальность полета прямо пропорциональна скорости бросания тела, следовательно, во сколько раз увеличим начальную скорость, во столько раз увеличится дальность полета тела.
Ответ. Дальность полета тела увеличится в $n$ раз.
Читать дальше: закон сообщающихся сосудов.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t – frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 – gt ]
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 – 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|
