Как найти найдите длину меньшей диагонали ромба

Все формулы длины диагоналей ромба

4. Диагонали пересекаются под прямым углом (90°)

5. Диагонали являются биссектрисами

Формулы диагоналей через сторону и угол, ( D d ):

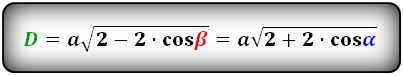
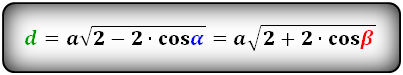
Формулы диагоналей через сторону и половинный угол, ( D d ):

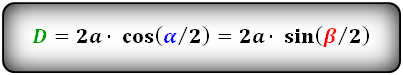
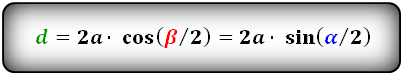
Формулы диагоналей через сторону и другую диагональ, ( D d ):

Формулы диагоналей через угол и другую диагональ, ( D d ):

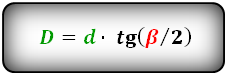
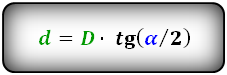
Формулы диагоналей через площадь ( D d ):

Источник

Ромб. Формулы, признаки и свойства ромба

Признаки ромба

∠BAC = ∠CAD или ∠BDA = ∠BDC

Δ ABO = Δ BCO = Δ CDO = Δ ADO

Основные свойства ромба

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

Сторона ромба

Формулы определения длины стороны ромба:

2. Формула стороны ромба через площадь и синус угла:

3. Формула стороны ромба через площадь и радиус вписанной окружности:

6. Формула стороны ромба через большую диагональ и половинный угол:

7. Формула стороны ромба через малую диагональ и половинный угол:

Диагонали ромба

Формулы определения длины диагонали ромба:

d ₁ = a √ 2 + 2 · cosα

d ₂ = a √ 2 + 2 · cosβ

d ₁ = 2 a · cos ( α /2)

d ₁ = 2 a · sin ( β /2)

d ₂ = 2 a · sin ( α /2)

d ₂ = 2 a · cos ( β /2)

7. Формулы диагоналей через площадь и другую диагональ:

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

Периметр ромба

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Площадь ромба

Формулы определения площади ромба:

4. Формула площади ромба через две диагонали:

5. Формула площади ромба через синус угла и радиус вписанной окружности:

6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):

S =	1	d 1 2 · tg ( α /2)
2

S =	1	d 2 2 · tg ( β /2)
2

Окружность вписанная в ромб

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

6. Формула радиуса круга вписанного в ромб через две диагонали:

r =	d 1 · d 2
2√ d 1 2 + d 2 2

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Чему равна длина меньшей диагонали ромба, если (см)?

Из него видно что мЕньшая диагональ равна 21.

Углы у ромба получаются 120,60,120,60.

Диагонали ромба пересекаются под прямым углом.

Ответ: меньшая диагональ ромба равна 21.

Задача решается на основе определений этой фигуры и предположений. Все стороны ромба равны, то есть- по 21, исходя из параметров ромб, в нём два угла острые и два- тупые, значит острые по 60 градусов, тупые по 120, рассмотрев один из четырех треугольников, полученных от пересечения диагоналей, находим их прямоугольными с гипотенузами, равными 21 и половинка малой диагонали равна 10,5, как катет, лежащий против угла в тридцать градусов, получается, что она тоже рана 21 и образовывает равносторонний треугольник, поскольку все углы- по 60 градусов и данный ромб делится диагоналями на два треугольника равносторонних и два равнобедренных- тупоугольных.

Из предоставленной записи задания можно только предположить что сумма [двух противоположных] углов равна 120°. Если это так, то получим ромб с острыми углами 60° и тупыми углами 120°. Короткая диагональ поделит ромб на для равносторонних треугольника и стороны его будут равны 0,25 или 1/4 периметра. Отсюда меньшая диагональ равна 21.

Данных не достаточно. Нет прямой зависимости площади ромба и его высоты. Для вычисления надо также знать один из двух параметров: или длину стороны, или размер угла между двумя соседними сторонами.

Один вариант прямой зависимости площади только от высоты возможен в одном случае, если ромб является квадратом (кроме сторон равны также все углы, а из того, что сума углов четырёхугольника = 360 градусов, то один угол равен 90). В таком случае сторона равняется высоте и, соответственно, корню квадратному из значения площади.

(для квадрата) h=a=sqrt(S). Но это только частный случай.

Во всех других случаях нужно ещё одну меру (сторона или угол)ромба.

Ромб имеет две оси симметрии второго порядка, (т.е. для совпадения нужно повернуть ромб вокруг этой оси на 1/2 полного оборота), в плоскости, в которой лежит ромб, и одну ось симметрии второго порядка, перпендикулярную плоскости, в которой лежит ромб.

Высоту ромба найти не так-то просто, как это может показаться с первого взгляда. Нужно сначала нарисовать эту высоту, а потом уже находить. А чтобы нарисовать, нужно продлить одну из сторон и тогда уже рисовать. Допустим у ромба сторона а. Острый угол- это б. Тогда высота равна h=acos(90-(б/2)), то есть h=a*sin(б/2).

И опять несложно определить одну из сторон, если известны площадь ромба и его высота:

нужно площадь разделить на высоту

сторона ромба равна половине корня квадратного от суммы квадратов диагоналей

на рисунке d1=D и d2=d

Также есть много других формул (более сложных), где сторону ромба можно найти через площадь и угол, через диагональ и угол и другие

Источник

Диагонали ромба

Ромб — частный случай параллелограмма, у которого все стороны равны, а противоположные — параллельны. Отрезки, соединяющие противоположные вершины ромба, называются его диагоналями. Они пересекаются между собой под прямым углом и делятся в точке пересечения пополам. Диагонали делят ромб на два равнобедренных треугольника и четыре одинаковых прямоугольных треугольника, у которых гипотенузой является сторона ромба (а), углом — половина угла ромба, сторонами (катетами) — половина диагоналей. Используя тригонометрические отношения находим катеты треугольника как произведение гипотенузы на синус и косинус половины известного угла. Чтобы найти второй угол, нужно из 180 градусов вычесть величину известного нам угла. Диагонали D, d ромба через сторону и половинный угол определяем по формуле:
где D — большая диагональ, d — меньшая диагональ ромба, a — сторона ромба, углы ромба α,β. Чтобы найти диагонали D, d через сторону и угол, воспользуемся формулами:

D = 2a × cos (α/2) = 2a × sin (β/2)

d = 2a × cos (β/2) = 2a × sin (α/2)

Если даны угол и сторона ромба, можно определить его высоту, как произведение стороны на синус угла. Произведение высоты на сторону ромба позволит определить его площадь. Площадь ромба через две его диагонали равна половине их произведений. Если известна площадь ромба и одна из его диагоналей, можно найти другую диагональ. Так как в ромбе все стороны равны, то его периметр равен произведению одной стороны на количество всех его сторон — четыре.

Источник

Как найти длину меньшей диагонали ромба

Здравствуйте!
Сторона у ромба равна 40 см, а острый угол этого ромба равен 60 градусов. Как найти длину меньшей диагонали ромба?
Помогите решить, пожалуйста!
Спасибо!

Задача.
Сторона у ромба равняется 40 см, а острый угол этого ромба равняется 60 градусов. Найти длину меньшей диагонали ромба.

Решение.
Построим ромб, сторона которого равна 40 см, а острый угол 60 градусов.
Проведем в нем диагонали. Как известно, у диагонали ромба делят углы при его вершинах пополам, следовательно, угол, который согласно условию равняется 60 градусов, поделится на два угла, равных по 30 градусов. Также диагонали ромба при пересечении составляют прямой угол. Следовательно, диагонали ромба разделят его на четыре равных треугольника, которые имеют углы, равные 30, 60 и 90 градусов.
Согласно одному из свойств прямоугольного треугольника, катет, который расположен напротив угла в 30 градусов, равен половине гипотенузы. В нашем прямоугольном треугольнике гипотенуза– это сторона данного ромба. По условию сторона ромба равна 40 см. Таким образом, катет прямоугольного треугольника будет равен 40 : 2 = 20 см.
Диагонали ромба точкой пересечения делятся пополам, поэтому вся меньшая диагональ будет равна двум таким катетам. Следовательно, меньшая диагональ равна 2 * 20 = 40 см.

Ответ. 40 см.

Подобным образом находится и бОльшая диагональ ромба. Рассматривается тот же прямоугольный треугольник, один катет и гипотенуза которого уже известны, а с помощью теоремы Пифагора можно найти и второй катет. Тогда вся бОльшая диагональ будет равна двум таким катетам.

Источник

Диагональ параллелограмма – это отрезок, соединяющий противоположные вершины фигуры. В зависимости от
вида геометрической фигуры диагональ обладает важными свойствами, на которые основываются базовые
правила и формулы. Рассмотрим подробнее, как найти длину данного отрезка, построенного в
параллелограмме с равными сторонами, т.е. ромбе.

Диагональ ромба через сторону и другую известную диагональ

В случае, если в ромбе известны значения одной диагонали (d) и стороны (a) фигуры, прийти к
определению длины второго отрезка будет несложно, благодаря тождеству параллелограмма, которое
гласит, что сумма квадратов диагоналей равна квадрату стороны, умноженному на 4:

d = √(4a² — d²)

где a — сторона, d — известная диагональ.

Пример. Дан ромб с диагональю равной 6 мм и стороной, длина которой 5 мм. Нужно
найти вторую диагональ ромба. d = √(4 * 5² — 6²) = √(4 * 25 — 36) = √(100 — 36) = √64 = 8 мм
– длина неизвестной диагонали.

Как найти длину большей диагонали через сторону и острый угол

Найти величину длинной диагонали можно по формуле:

d = a * √(2 + 2 * cos α)

где a — сторона, cos α — острый угол.

Проведенный отрезок, который соединяет противоположные вершины фигуры, делит ее на равнобедренные
треугольники. По свойствам равнобедренного треугольника косинус углов при основании равен половине
основания (в данном случае диагонали), деленного на боковую сторону (сторону ромба).

Пример. Острый угол между сторонами ромба длиной 6 см равен 45 градусам. Найти
биссектрису острого угла ромба (в данном случае диагональ). d = 6 * √(2 + 2 * cos 45°) = 6 * √(2 + 2 * √2 / 2) = 6 * √(2 + 2 * 0,7) = 11см
– длинна неизвестного отрезка.

Как найти длину большей диагонали через сторону и известное значение тупого угла

Как уже известно, построенная диагональ в ромбе, делит его на 2 равнобедренных треугольника. Если
дополнить картину второй проведенной диагональю, получится прямоугольный треугольник. Косинус
половинки тупого угла (c) это отношение прилежащего катета к гипотенузе (стороне ромба a). На
основании всех этих свойств можно прийти к простой формуле нахождения нужной диагонали через сторону
ромба (в данном случае гипотенузу) и косинус тупого угла:

d = a * √( 2 — 2 * cos β)

где a — сторона, cos β — тупой угол

Пример. Дан ромб со стороной 4,65 м, величина тупого угла которого равна 120
градусам. Необходимо найти противолежащую известному углу диагональ. d = 4,65 * √(2 — 2 * cos 120°) = 4,65 * √(2 — 2 * (-0,5) = 8 м
– длина неизвестного отрезка.

Как вычислить длину меньшей диагонали через сторону и острый угол

Так как ситуация аналогична предыдущей (только известный противолежащий угол острый), формула
нахождения короткой диагонали практически ничем не отличается от алгоритма определения длинного
отрезка, соединяющего противолежащие вершины ромба.

d = a * √(2 — 2 * cos α)

где a — сторона, cos α — острый угол

Пример. В ромбе со стороной 4,65 м проведена диагональ, которая является основанием
равнобедренного треугольника с углом при вершине равным 52 градусам. Найти основание треугольника
(меньшую диагональ). d = 4,65 * √(2 — 2 * cos 52°) = 4 м.

Короткая диагональ ромба через длинную диагональ и острый угол

Аналогично с предыдущей ситуацией, через тангенс острого угла находим величину неизвестного катета
(половинку искомой диагонали). Упрощенная формула:

d = D * tg (α / 2)

где D — длинная диагональ, α — острый угол

Пример. Острый угол ромба, в котором построена диагональ длиной 11 мм, равен 58
градусам. Найти длину второй диагонали. d = 11 * tg 29° = 6 мм – длина
меньшей диагонали ромба.

Короткая диагональ через сторону и тупой угол

Формула для нахождения меньшей диагонали ромба при помощи значения стороны и тупого угла такова:

d = a * √(2 + 2 * cos β)

где a — сторона, cos β — тупой угол

Пример. Дан ромб со стороной 4,65 мм, один из углов которого равен 128 градусов, а
меньшая диагональ фигуры – искомая величина. d = a * √(2 + 2 * cos β) = 4,65 *  √(2 + 2 * cos 128°) = 4 мм.

Длинная диагональ ромба через короткую диагональ и тупой угол

Длина большей диагонали ромба легко находится по формуле:

D = d * tg (β / 2)

где d — короткая диагональ, β — тупой угол

Благодаря теореме Пифагора, зная длину короткой диагонали (половина катета прямоугольного
треугольника) и значение тупого угла ромба (половина которого является углом прямоугольного
треугольника), не составит труда определить значение большей диагонали ромба через тангенс тупого
угла.

Пример. Дан ромб с диагональю 6,5 см, которая является биссектрисой тупого угла
величиной 119 градусов. Нужно найти неизвестную диагональ ромба. D = 6,5 * tg (119 / 2) = 11 см
– искомая величина.

Диагональ ромба через площадь и другую известную диагональ

Найти любую из двух диагоналей ромба можно по формуле:

D = 2 * S / d

где d – длина известного отрезка, а S-площадь фигуры.

Пример. Дан ромб с площадью равной 64 см², его диагональ равна 8,5 см. Необходимо
найти длину второго отрезка, соединяющего противолежащие вершины. D = 2 * S / d = 2 * 64 / 8,5 = 15 см.

Ромб относится к плоским выпуклым геометрическим фигурам. Данный вид параллелограмма отличается
равными сторонами, а также тем, что его диагонали при пересечении перпендикулярны друг другу.
Существуют и другие свойства ромба, которые подробно раскрывают смысл указанных выше формул:

• Диагонали, пересекаясь под прямым углом, делятся точкой пересечения пополам. Таким образом, они
  всегда разделяют фигуру на 4 прямоугольных треугольника.
• Противоположные стороны ромба попарно параллельны.
• Противолежащие углы равны, а смежные – в сумме образуют 180 градусов.
• Диагонали служат биссектрисами всех углов ромба.
• Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
• Если соединить середины сторон ромба, получится прямоугольник.
• Точка пересечения диагоналей — центр вписанной окружности.

Определение диагонали ромба часто встречается в задачах школьной программы. Найдя данное значение,
можно прийти к искомому результату задания. Через диагональ можно найти стороны ромба, площадь,
периметр и все внутренние углы ромба.

Геометрия в школьной программе включается в себя немалое количество формул, основанных на теоремах и
правилах. Некоторые из которых помогают значительно сократить время для решения задач на контрольной
или при выполнении домашней работы. Данная статья поможет быстро прийти к логическому решению
задания и правильному результату. Знание и применение выше перечисленных формул способствуют умению
решать задачи по геометрии любой сложности.

Задача.
Сторона у ромба равняется 40 см, а острый угол этого ромба равняется 60 градусов. Найти длину меньшей диагонали ромба.

 
Решение.
Построим ромб, сторона которого равна 40 см, а острый угол 60 градусов.
Проведем в нем диагонали. Как известно, у диагонали ромба делят углы при его вершинах пополам, следовательно, угол, который согласно условию равняется 60 градусов, поделится на два угла, равных по 30 градусов. Также диагонали ромба при пересечении составляют прямой угол. Следовательно, диагонали ромба разделят его на четыре равных треугольника, которые имеют углы, равные 30, 60 и 90 градусов.
Согласно одному из свойств прямоугольного треугольника, катет, который расположен напротив угла в 30 градусов, равен половине гипотенузы. В нашем прямоугольном треугольнике гипотенуза– это сторона данного ромба. По условию сторона ромба равна 40 см. Таким образом, катет прямоугольного треугольника будет равен 40 : 2 = 20 см.
Диагонали ромба точкой пересечения делятся пополам, поэтому вся меньшая диагональ будет равна двум таким катетам. Следовательно, меньшая диагональ равна 2 * 20 = 40 см.

 
Ответ. 40 см.

 
Подобным образом находится и бОльшая диагональ ромба. Рассматривается тот же прямоугольный треугольник, один катет и гипотенуза которого уже известны, а с помощью теоремы Пифагора можно найти и второй катет. Тогда вся бОльшая диагональ будет равна двум таким катетам.

На клетчатой бумаге с размером клетки 1 х 1 изображён ромб. Найдите длину его большей диагонали.

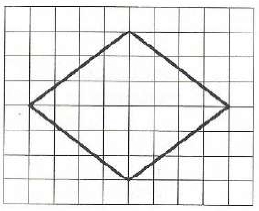
Источник: ОГЭ Ященко 2022 (36 вар)

Решение:

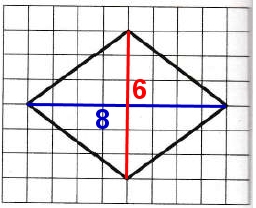
    Диагонали ромба равны 6 и 8 клеток. Большая из них 8 клеток.

Ответ: 8.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.8 / 5. Количество оценок: 12

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

• Запись опубликована:11.01.2022
• Рубрика записи18. Фигуры на квадратной решётке
• Автор записи:Andrei Maniakin