Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Уравнение прямой касательной к графику функции в заданной точке
Эта математическая программа находит уравнение касательной к графику функции ( f(x) ) в заданной пользователем точке ( x_0 ).
Программа не только выводит уравнение касательной, но и отображает процесс решения задачи.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Статью из энциклопедии о касательной прямой вы можете посмотреть здесь (статья из Википедии).
Если вам нужно найти производную функции, то для этого у нас есть задача Найти производную.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> Введите выражение функции ( f(x)) и число (x_0) – абсциссу точки в которой нужно построить касательную Найти уравнение касательной
Немного теории.
Угловой коэффициент прямой
Напомним, что графиком линейной функции ( y=kx+b) является прямая. Число (k=tg alpha ) называют угловым коэффициентом прямой, а угол ( alpha ) – углом между этой прямой и осью Ox
Уравнение касательной к графику функции
Если точка М(а; f(a)) принадлежит графику функции у = f(x) и если в этой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то из геометрического смысла производной следует, что угловой коэффициент касательной равен f'(a). Далее мы выработаем алгоритм составления уравнения касательной к графику любой функции.
Пусть даны функция у = f(x) и точка М(а; f(a)) на графике этой функции; пусть известно, что существует f'(a). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид y = kx + b, поэтому задача состоит в нахождении значений коэффициентов k и b.
С угловым коэффициентом k все понятно: известно, что k = f'(a). Для вычисления значения b воспользуемся тем, что искомая прямая проходит через точку М(а; f(a)). Это значит, что если подставить координаты точки М в уравнение прямой, получим верное равенство: (f(a)=ka+b ), т.е. ( b = f(a) – ka ).
Осталось подставить найденные значения коэффициентов k и b в уравнение прямой:
Нами получено уравнение касательной к графику функции ( y = f(x) ) в точке ( x=a ).
Алгоритм нахождения уравнения касательной к графику функции ( y=f(x) )
1. Обозначить абсциссу точки касания буквой ( a )
2. Вычислить ( f(a) )
3. Найти (f'(x) ) и вычислить (f'(a) )
4. Подставить найденные числа ( a, f(a), f'(a) ) в формулу ( y=f(a)+ f'(a)(x-a) )
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.

На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .
- Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
- Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
- Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
- Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
Определение 3
Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α – красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
k = t g α = B C A C = f ( x B ) – f x A x B – x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) – это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) – f ( x A ) x B – x A или k = f ( x A ) – f ( x B ) x A – x B , причем уравнение необходимо записать как y = f ( x B ) – f ( x A ) x B – x A · x – x A + f ( x A ) или
y = f ( x A ) – f ( x B ) x A – x B · x – x B + f ( x B ) .
Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y = 2 x сливается с прямой у = х + 1 .
Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.

Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .
Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) – f ( ∆ x ) . Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .
Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.
То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x – x 0 + f ( x 0 ) .
Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 – 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 – 0 f ‘ ( x ) .
Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у – k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .
Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 – 6 – 3 3 x – 17 – 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = – 1 , f ( x 0 ) = – 3 .
Необходимо найти производную в точке со значением – 1 . Получаем, что
y ‘ = e x + 1 + x 3 3 – 6 – 3 3 x – 17 – 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ – 6 – 3 3 x ‘ – 17 – 3 3 ‘ = e x + 1 + x 2 – 6 – 3 3 y ‘ ( x 0 ) = y ‘ ( – 1 ) = e – 1 + 1 + – 1 2 – 6 – 3 3 = 3 3
Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3
Отсюда следует, что α x = a r c t g 3 3 = π 6
Ответ: уравнение касательной приобретает вид
y = f ‘ ( x 0 ) · x – x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) – 3 y = 3 3 x – 9 – 3 3
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Выяснить наличие существования касательной к графику заданной функции
y = 3 · x – 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y ‘ = 3 · x – 1 5 + 1 ‘ = 3 · 1 5 · ( x – 1 ) 1 5 – 1 = 3 5 · 1 ( x – 1 ) 4 5
Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x – 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 – 0 3 5 · 1 ( x – 1 ) 4 5 = 3 5 · 1 ( – 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .
Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .
Для наглядности изобразим графически.

Найти точки графика функции y = 1 15 x + 2 3 – 4 5 x 2 – 16 5 x – 26 5 + 3 x + 2 , где
- Касательная не существует;
- Касательная располагается параллельно о х ;
- Касательная параллельна прямой y = 8 5 x + 4 .
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ – ∞ ; 2 и [ – 2 ; + ∞ ) . Получаем, что
y = – 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ – ∞ ; – 2 1 15 x 3 – 6 x 2 + 9 x + 12 , x ∈ [ – 2 ; + ∞ )
Необходимо продифференцировать функцию. Имеем, что
y ‘ = – 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ – ∞ ; – 2 1 15 x 3 – 6 x 2 + 9 x + 12 ‘ , x ∈ [ – 2 ; + ∞ ) ⇔ y ‘ = – 1 5 ( x 2 + 12 x + 35 ) , x ∈ – ∞ ; – 2 1 5 x 2 – 4 x + 3 , x ∈ [ – 2 ; + ∞ )
Когда х = – 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:
lim x → – 2 – 0 y ‘ ( x ) = lim x → – 2 – 0 – 1 5 ( x 2 + 12 x + 35 = – 1 5 ( – 2 ) 2 + 12 ( – 2 ) + 35 = – 3 lim x → – 2 + 0 y ‘ ( x ) = lim x → – 2 + 0 1 5 ( x 2 – 4 x + 3 ) = 1 5 – 2 2 – 4 – 2 + 3 = 3
Вычисляем значение функции в точке х = – 2 , где получаем, что
- y ( – 2 ) = 1 15 – 2 + 2 3 – 4 5 ( – 2 ) 2 – 16 5 ( – 2 ) – 26 5 + 3 – 2 + 2 = – 2 , то есть касательная в точке ( – 2 ; – 2 ) не будет существовать.
- Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .
Когда x ∈ – ∞ ; – 2 , тогда – 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( – 2 ; + ∞ ) получаем 1 5 ( x 2 – 4 x + 3 ) = 0 .
– 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 – 4 · 35 = 144 – 140 = 4 x 1 = – 12 + 4 2 = – 5 ∈ – ∞ ; – 2 x 2 = – 12 – 4 2 = – 7 ∈ – ∞ ; – 2 1 5 ( x 2 – 4 x + 3 ) = 0 D = 4 2 – 4 · 3 = 4 x 3 = 4 – 4 2 = 1 ∈ – 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ – 2 ; + ∞
Вычисляем соответствующие значения функции
y 1 = y – 5 = 1 15 – 5 + 2 3 – 4 5 – 5 2 – 16 5 – 5 – 26 5 + 3 – 5 + 2 = 8 5 y 2 = y ( – 7 ) = 1 15 – 7 + 2 3 – 4 5 ( – 7 ) 2 – 16 5 – 7 – 26 5 + 3 – 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 – 4 5 · 1 2 – 16 5 · 1 – 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 – 4 5 · 3 2 – 16 5 · 3 – 26 5 + 3 3 + 2 = 4 3
Отсюда – 5 ; 8 5 , – 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ – ∞ ; – 2 , получаем, что – 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( – 2 ; + ∞ ) , тогда 1 5 ( x 2 – 4 x + 3 ) = 8 5 .
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
– 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 – 4 · 43 = – 28 0
Другое уравнение имеет два действительных корня, тогда
1 5 ( x 2 – 4 x + 3 ) = 8 5 x 2 – 4 x – 5 = 0 D = 4 2 – 4 · ( – 5 ) = 36 x 1 = 4 – 36 2 = – 1 ∈ – 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ – 2 ; + ∞
Перейдем к нахождению значений функции. Получаем, что
y 1 = y ( – 1 ) = 1 15 – 1 + 2 3 – 4 5 ( – 1 ) 2 – 16 5 ( – 1 ) – 26 5 + 3 – 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 – 4 5 · 5 2 – 16 5 · 5 – 26 5 + 3 5 + 2 = 8 3
Точки со значениями – 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .
Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках – 1 ; 4 15 , 5 ; 8 3 .

Возможно существование бесконечного количества касательных для заданных функций.
Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x – π 4 – 1 3 , которые располагаются перпендикулярно прямой y = – 2 x + 1 2 .
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется – 1 , то есть записывается как k x · k ⊥ = – 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = – 2 , тогда k x = – 1 k ⊥ = – 1 – 2 = 1 2 .
Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.
y ‘ ( x 0 ) = 3 cos 3 2 x 0 – π 4 – 1 3 ‘ = 3 · – sin 3 2 x 0 – π 4 · 3 2 x 0 – π 4 ‘ = = – 3 · sin 3 2 x 0 – π 4 · 3 2 = – 9 2 · sin 3 2 x 0 – π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ – 9 2 · sin 3 2 x 0 – π 4 = 1 2 ⇒ sin 3 2 x 0 – π 4 = – 1 9
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
3 2 x 0 – π 4 = a r c sin – 1 9 + 2 πk или 3 2 x 0 – π 4 = π – a r c sin – 1 9 + 2 πk
3 2 x 0 – π 4 = – a r c sin 1 9 + 2 πk или 3 2 x 0 – π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 – a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z – множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у :
y 0 = 3 cos 3 2 x 0 – π 4 – 1 3
y 0 = 3 · 1 – sin 2 3 2 x 0 – π 4 – 1 3 или y 0 = 3 · – 1 – sin 2 3 2 x 0 – π 4 – 1 3
y 0 = 3 · 1 – – 1 9 2 – 1 3 или y 0 = 3 · – 1 – – 1 9 2 – 1 3
y 0 = 4 5 – 1 3 или y 0 = – 4 5 + 1 3
Отсюда получаем, что 2 3 π 4 – a r c sin 1 9 + 2 πk ; 4 5 – 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; – 4 5 + 1 3 являются точками касания.
Ответ: необходимы уравнения запишутся как
y = 1 2 x – 2 3 π 4 – a r c sin 1 9 + 2 πk + 4 5 – 1 3 , y = 1 2 x – 2 3 5 π 4 + a r c sin 1 9 + 2 πk – 4 5 + 1 3 , k ∈ Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [ – 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = – 2 x + 1 2 . Красные точки – это точки касания.

Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x – x c e n t e r 2 + y – y c e n t e r 2 = R 2 .
Данное равенство может быть записано как объединение двух функций:
y = R 2 – x – x c e n t e r 2 + y c e n t e r y = – R 2 – x – x c e n t e r 2 + y c e n t e r
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 – x – x c e n t e r 2 + y c e n t e r или y = – R 2 – x – x c e n t e r 2 + y c e n t e r в указанной точке.
Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r – R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r – R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r – R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r – R .

Касательная к эллипсу
Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x – x c e n t e r 2 a 2 + y – y c e n t e r 2 b 2 = 1 .
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y = b a · a 2 – ( x – x c e n t e r ) 2 + y c e n t e r y = – b a · a 2 – ( x – x c e n t e r ) 2 + y c e n t e r

Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.

Написать уравнение касательной к эллипсу x – 3 2 4 + y – 5 2 25 = 1 в точках со значениями x равного х = 2 .
Решение
Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что
x – 3 2 4 x = 2 + y – 5 2 25 = 1 1 4 + y – 5 2 25 = 1 ⇒ y – 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5
Тогда 2 ; 5 3 2 + 5 и 2 ; – 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что
x – 3 2 4 + y – 5 2 25 = 1 y – 5 2 25 = 1 – x – 3 2 4 ( y – 5 ) 2 = 25 · 1 – x – 3 2 4 y – 5 = ± 5 · 1 – x – 3 2 4 y = 5 ± 5 2 4 – x – 3 2
Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 – x – 3 2 , а нижний y = 5 – 5 2 4 – x – 3 2 .
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
y ‘ = 5 + 5 2 4 – x – 3 2 ‘ = 5 2 · 1 2 4 – ( x – 3 ) 2 · 4 – ( x – 3 ) 2 ‘ = = – 5 2 · x – 3 4 – ( x – 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = – 5 2 · 2 – 3 4 – ( 2 – 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x – x 0 + y 0 ⇔ y = 5 2 3 ( x – 2 ) + 5 3 2 + 5
Получаем, что уравнение второй касательной со значением в точке
2 ; – 5 3 2 + 5 принимает вид
y ‘ = 5 – 5 2 4 – ( x – 3 ) 2 ‘ = – 5 2 · 1 2 4 – ( x – 3 ) 2 · 4 – ( x – 3 ) 2 ‘ = = 5 2 · x – 3 4 – ( x – 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 – 3 4 – ( 2 – 3 ) 2 = – 5 2 3 ⇒ y = y ‘ ( x 0 ) · x – x 0 + y 0 ⇔ y = – 5 2 3 ( x – 2 ) – 5 3 2 + 5
Графически касательные обозначаются так:

Касательная к гиперболе
Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r – α ; y c e n t e r , имеет место задание неравенства x – x c e n t e r 2 α 2 – y – y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r – b , тогда задается при помощи неравенства x – x c e n t e r 2 α 2 – y – y c e n t e r 2 b 2 = – 1 .

Гипербола может быть представлена в виде двух объединенных функций вида
y = b a · ( x – x c e n t e r ) 2 – a 2 + y c e n t e r y = – b a · ( x – x c e n t e r ) 2 – a 2 + y c e n t e r или y = b a · ( x – x c e n t e r ) 2 + a 2 + y c e n t e r y = – b a · ( x – x c e n t e r ) 2 + a 2 + y c e n t e r

В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Составить уравнение касательной к гиперболе x – 3 2 4 – y + 3 2 9 = 1 в точке 7 ; – 3 3 – 3 .
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x – 3 2 4 – y + 3 2 9 = 1 ⇒ y + 3 2 9 = x – 3 2 4 – 1 ⇒ y + 3 2 = 9 · x – 3 2 4 – 1 ⇒ y + 3 = 3 2 · x – 3 2 – 4 и л и y + 3 = – 3 2 · x – 3 2 – 4 ⇒ y = 3 2 · x – 3 2 – 4 – 3 y = – 3 2 · x – 3 2 – 4 – 3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; – 3 3 – 3 .
Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 – 3 ) 2 – 4 – 3 = 3 3 – 3 ≠ – 3 3 – 3 , тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y ( 7 ) = – 3 2 · ( 7 – 3 ) 2 – 4 – 3 = – 3 3 – 3 ≠ – 3 3 – 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
y ‘ = – 3 2 · ( x – 3 ) 2 – 4 – 3 ‘ = – 3 2 · x – 3 ( x – 3 ) 2 – 4 ⇒ k x = y ‘ ( x 0 ) = – 3 2 · x 0 – 3 x 0 – 3 2 – 4 x 0 = 7 = – 3 2 · 7 – 3 7 – 3 2 – 4 = – 3
Ответ: уравнение касательной можно представить как
y = – 3 · x – 7 – 3 3 – 3 = – 3 · x + 4 3 – 3
Наглядно изображается так:

Касательная к параболе
Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x – x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .
Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что
x = a y 2 + b y + c ⇔ a y 2 + b y + c – x = 0 D = b 2 – 4 a ( c – x ) y = – b + b 2 – 4 a ( c – x ) 2 a y = – b – b 2 – 4 a ( c – x ) 2 a
Графически изобразим как:

Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.
Написать уравнение касательной к графику x – 2 y 2 – 5 y + 3 , когда имеем угол наклона касательной 150 ° .
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
– 2 y 2 – 5 y + 3 – x = 0 D = ( – 5 ) 2 – 4 · ( – 2 ) · ( 3 – x ) = 49 – 8 x y = 5 + 49 – 8 x – 4 y = 5 – 49 – 8 x – 4
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = – 1 3
Отсюда определим значение х для точек касания.
Первая функция запишется как
y ‘ = 5 + 49 – 8 x – 4 ‘ = 1 49 – 8 x ⇒ y ‘ ( x 0 ) = 1 49 – 8 x 0 = – 1 3 ⇔ 49 – 8 x 0 = – 3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
Вторая функция запишется как
y ‘ = 5 – 49 – 8 x – 4 ‘ = – 1 49 – 8 x ⇒ y ‘ ( x 0 ) = – 1 49 – 8 x 0 = – 1 3 ⇔ 49 – 8 x 0 = – 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 – 49 – 8 · 23 4 – 4 = – 5 + 3 4
Имеем, что точки касания – 23 4 ; – 5 + 3 4 .
Ответ: уравнение касательной принимает вид
Касательная и нормаль к графику функции
Основные формулы
Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной
Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓
Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓
Определения
Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.
Определение касательной приводится здесь. Уравнение касательной:
.
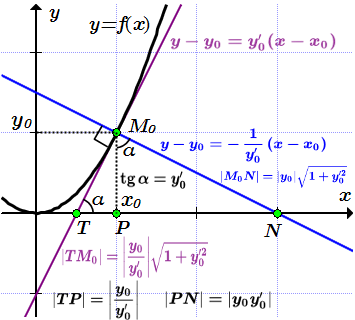
 Касательная TM0, нормаль M0N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
Касательная TM0, нормаль M0N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
.
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .
Полезные формулы из аналитической геометрии
Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.
Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.
Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .
Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :
Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.
Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.
Уравнение прямой в отрезках, пересекающей оси координат в точках :
.
Примеры решения задач
Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓
Пример 1
Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.
Находим значение функции при :
.
Находим производную:
.
Находим производную в точке :
;
.
Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .
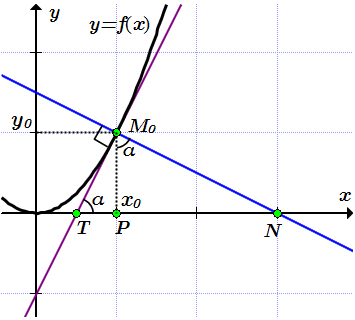 Касательная и нормаль к графику функции y=x 2 в точке M0(1;1).
Касательная и нормаль к графику функции y=x 2 в точке M0(1;1).
Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.
Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .
Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.
Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка поднормали . Из прямоугольника имеем:
.
Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.
Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .
Пример 2
Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .
Находим значения переменных при .
;
.
Обозначим эту точку как .
Находим производные переменных x и y по параметру t .
;
;
;
;
.
Подставляя , находим производную y по x в точке .
.
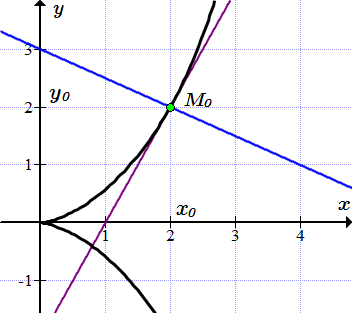 Касательная и нормаль к циссоиде в точке (2;2).
Касательная и нормаль к циссоиде в точке (2;2).
Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.
Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.
Уравнение касательной: .
Уравнение нормали: .
Пример 3
Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .
Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.
Находим производную в заданной точке, подставляя .
;
.
Находим уравнение касательной по формуле (2).
;
;
;
.
Находим уравнение нормали по формуле (3).
;
;
;
.
Касательная и нормаль к циссоиде изображены на рисунке ⇑.
Уравнение касательной: .
Уравнение нормали: .
Пример 4
Найти угол между кривыми и .
Найдем множество точек пересечения кривых, решая систему уравнений.
Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .
Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.
Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.
Вывод формулы для угла между кривыми
Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .
Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .
Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.
В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .
На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .
При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.
1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).
2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:
.
Этот случай изображен на рисунке ⇑.
3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).
Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.
Автор: Олег Одинцов . Опубликовано: 30-06-2021
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/proizvodnye/kasatelnaja-k-grafiku-funktsii-v-tochke/
http://1cov-edu.ru/mat-analiz/proizvodnaya/kasatelnaya-i-normal-k-grafiku-funktsii/
[/spoiler]
|
Как найти тангенс угла наклона касательной? Касательной называется прямая проходящая через точку, принадлежащую кривой линии или кривой поверхности. Касательная прямая всегда перпендикулярна к радиусу кривизны. Касательной к окружности с центром О называется прямая имеющая только одну общую точку с окружностью, называемую точкой касания К. Через одну точку А, расположенную вне окружности, можно провести только две касательные, которые симметричны относительно прямой проходящей через эту точку А и центр окружности О. Для единичной окружности тангенс угла наклона касательной АК равен 1/АК. система выбрала этот ответ лучшим Вопрос не совсем понятен. Не понятно какие входные данные. Могу предположить, что надо найти тангенс угла между касательной и осью абсцисс (осью Ох) в какой то точке графика функции. Функция задана аналитически, т.е. формулой. В таком случае: надо найти первую производную данной функции и посчитать значение этой производной в нужной точке. В итоге получим значение тангенса угла между касательной и осью Ох. Если надо знать угол, то по известному тангенсу угла, ищем значение самого угла. Знаете ответ? |
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Угловой коэффициент касательной как тангенс угла наклона
(blacktriangleright) Если уравнение прямой задано в виде ({color{royalblue}{y=kx+b ;}}), то число (k) называется угловым коэффициентом.
(blacktriangleright) Угол (alpha) наклона прямой – это угол между этой прямой и положительным направлением оси (Ox) ((0leqslant
alpha< 180^circ)), лежащий в верхней полуплоскости.
(blacktriangleright) Основная формула. Угловой коэффициент прямой (y=kx+b) равен тангенсу угла наклона этой прямой:
[{large{color{royalblue}{k=mathrm{tg}, alpha}}}]
Т.к. касательная к графику некоторой функции — это и есть прямая, то для нее верны все эти утверждения.

Если (alpha<90^circ), то (k>0);
если (alpha>90^circ), то (k<0);
если (alpha=0^circ), то (k=0) (уравнение прямой имеет вид (y=b) и она параллельна оси (Ox));
если (alpha=90^circ), то уравнение прямой имеет вид (x=a) и она перпендикулярна оси (Ox).
Задание
1
#685
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = x), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = x) коэффициент (k) равен (1), то (mathrm{tg}, alpha = 1).
Ответ: 1
Задание
2
#686
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = 2x – 3), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
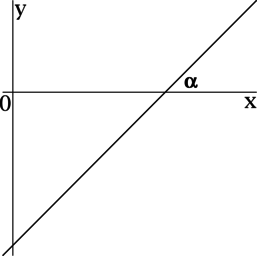
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = 2x – 3) коэффициент (k) равен (2), то (mathrm{tg}, alpha = 2).
Ответ: 2
Задание
3
#687
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = -x + 2), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
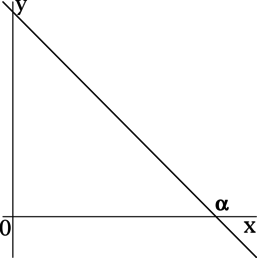
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = -x + 2) коэффициент (k) равен (-1), то (mathrm{tg}, alpha = -1).
Ответ: -1
Задание
4
#688
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx + 77), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = 12).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx + 77) и положительным направлением оси (Ox) равен (12), то (k = mathrm{tg}, alpha = 12).
Ответ: 12
Задание
5
#689
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx + 0,2), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = -3,3).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx + 0,2) и положительным направлением оси (Ox) равен (-3,3), то (k = mathrm{tg}, alpha = -3,3).
Ответ: -3,3
Задание
6
#690
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = 0).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx) и положительным направлением оси (Ox) равен (0), то (k = mathrm{tg}, alpha = 0).
Ответ: 0
Задание
7
#693
Уровень задания: Легче ЕГЭ
Прямая (y = kx – 2016) образует угол (45^{circ}) с положительным направлением оси (Ox). Найдите (k).
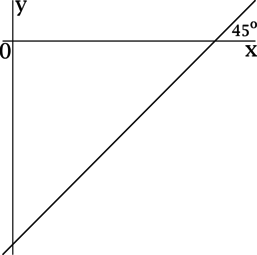
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как угол между прямой (y = kx – 2016) и положительным направлением оси (Ox) равен (dfrac{pi}{4}), то (k = mathrm{tg}, dfrac{pi}{4} = 1).
Ответ: 1
Теме «Угловой коэффициент касательной как тангенс угла наклона» в аттестационном экзамене отводится сразу несколько заданий. В зависимости от их условия, от выпускника может требоваться как полный ответ, так и краткий. При подготовке к сдаче ЕГЭ по математике ученику обязательно стоит повторить задачи, в которых требуется вычислить угловой коэффициент касательной.
Сделать это вам поможет образовательный портал «Школково». Наши специалисты подготовили и представили теоретический и практический материал максимально доступно. Ознакомившись с ним, выпускники с любым уровнем подготовки смогут успешно решать задачи, связанные с производными, в которых требуется найти тангенс угла наклона касательной.
Основные моменты
Для нахождения правильного и рационального решения подобных заданий в ЕГЭ необходимо вспомнить базовое определение: производная представляет собой скорость изменения функции; она равна тангенсу угла наклона касательной, проведенной к графику функции в определенной точке. Не менее важно выполнить чертеж. Он позволит найти правильное решение задач ЕГЭ на производную, в которых требуется вычислить тангенс угла наклона касательной. Для наглядности лучше всего выполнить построение графика на плоскости ОХY.
Если вы уже ознакомились с базовым материалом на тему производной и готовы приступить к решению задач на вычисление тангенса угла наклона касательной, подобных заданиям ЕГЭ, сделать это можно в режиме онлайн. Для каждого задания, например, задач на тему «Связь производной со скоростью и ускорением тела», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут попрактиковаться в выполнении задач различного уровня сложности. В случае необходимости упражнение можно сохранить в разделе «Избранное», чтобы потом обсудить решение с преподавателем.

УСТАЛ? Просто отдохни
Download Article
Download Article
Unlike a straight line, a curve’s slope constantly changes as you move along the graph. Calculus introduces students to the idea that each point on this graph could be described with a slope, or an “instantaneous rate of change.” The tangent line is a straight line with that slope, passing through that exact point on the graph. To find the equation for the tangent, you’ll need to know how to take the derivative of the original equation.
-

1
Sketch the function and tangent line (recommended). A graph makes it easier to follow the problem and check whether the answer makes sense. Sketch the function on a piece of graph paper, using a graphing calculator as a reference if necessary. Sketch the tangent line going through the given point. (Remember, the tangent line runs through that point and has the same slope as the graph at that point.)
-
Example 1: Sketch the graph of the parabola
. Draw the tangent going through point (-6, -1).
You don’t know the tangent’s equation yet, but you can already tell that its slope is negative, and that its y-intercept is negative (well below the parabola vertex with y value -5.5). If your final answer doesn’t match these details, you’ll know to check your work for mistakes.
-
Example 1: Sketch the graph of the parabola
-

2
Take the first derivative to find the equation for the slope of the tangent line.[1]
For function f(x), the first derivative f'(x) represents the equation for the slope of the tangent line at any point on f(x). There are many ways to take derivatives. Here’s a simple example using the power rule:[2]
Advertisement
-

3
Enter the x value of the point you’re investigating.[3]
Read the problem to discover the coordinates of the point for which you’re finding the tangent line. Enter the x-coordinate of this point into f'(x). The output is the slope of the tangent line at this point.-
Example 1 (cont.): The point mentioned in the problem is (-6, -1). Use the x-coordinate -6 as the input for f'(x):
f'(-6) = -6 + 3 = -3
The slope of the tangent line is -3.
-
Example 1 (cont.): The point mentioned in the problem is (-6, -1). Use the x-coordinate -6 as the input for f'(x):
-

4
Write the tangent line equation in point-slope form. The point-slope form of a linear equation is
, where m is the slope and
is a point on the line.[4]
You now have all the information you need to write the tangent line’s equation in this form. -

5
Confirm the equation on your graph. If you have a graphing calculator, graph the original function and the tangent line to check that you have the correct answer. If working on paper, refer to your earlier graph to make sure there are no glaring mistakes in your answer.
- Example 1 (cont.): The initial sketch showed that the slope of the tangent line was negative, and the y-intercept was well below -5.5. The tangent line equation we found is y = -3x – 19 in slope-intercept form, meaning -3 is the slope and -19 is the y-intercept. Both of these attributes match the initial predictions.
-

6
Try a more difficult problem. Here’s a run-through of the whole process again. This time, the goal is to find the line tangent to
at x = 2:
Advertisement
-

1
Find the extreme points on a graph. These are points where the graph reaches a local maximum (a point higher than the points on either side), or local minimum (lower than the points on either side). The tangent line always has a slope of 0 at these points (a horizontal line), but a zero slope alone does not guarantee an extreme point. Here’s how to find them:[5]
- Take the first derivative of the function to get f'(x), the equation for the tangent’s slope.
- Solve for f'(x) = 0 to find possible extreme points.
- Take the second derivative to get f”(x), the equation that tells you how quickly the tangent’s slope is changing.
- For each possible extreme point, plug the x-coordinate a into f”(x). If f”(a) is positive, there is a local minimum at a. If f”(a) is negative, there is a local maximum. If f”(a) is 0, there is an inflection point, not an extreme point.
- If there is a maximum or minimum at a, find f(a) to get the y-coordinate.
-

2
Find the equation of the normal. The “normal” to a curve at a particular point passes through that point, but has a slope perpendicular to a tangent. To find the equation for the normal, take advantage of the fact that (slope of tangent)(slope of normal) = -1, when they both pass through the same point on the graph.[6]
In other words:- Find f'(x), the slope of the tangent line.
- If the point is at x = a, find f'(a) to find the slope of the tangent at that point.
- Calculate
to find the slope of the normal.
- Write the normal equation in slope-point form.
Advertisement
Add New Question
-
Question
How do you calculate the slope of a tangent line?

Jake Adams
Academic Tutor & Test Prep Specialist
Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.

Academic Tutor & Test Prep Specialist
Expert Answer
-
Question
How do I find the equations of 2 lines that are tangent to a graph given the slope?

The equation for a line is, in general, y=mx+c. To find the equations for lines, you need to find m and c. m is the slope. For example, if your line goes up two units in the y direction, for every three units across in the x direction, then m=2/3. If you have the slope, m, then all you need now is c. To find c in any line, you can use any (x,y) points you know. In the case of a line that is tangent to a graph, you can use the point (x,y) where the line touches the graph. If you use that x and that y and the slope m, you can use algebra to find c. y=mx+c, so, c=y-mx. Once you have c, you have the equation of the line! Done.
-
Question
How do I find the equation of the line that is tangent to the graph of f(x) and parallel to the line y = 2x + 3?

Parallel lines always have the same slope, so since y = 2x + 3 has a slope of 2 (since it’s in slope-intercept form), the tangent also has a slope of 2. Now you also know that f'(x) will equal 2 at the point the tangent line passes through. Differentiate to get the equation for f'(x), then set it equal to 2. Now you can solve for x to find your x-coordinate, plug that into f(x) to find the y-coordinate, and use all the information you’ve found to write the tangent line equation in point-slope form.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
If necessary, start by rewriting the initial equation in standard form: f(x) = … or y = …
Advertisement
Video
About This Article
Article SummaryX
To find the equation of a tangent line, sketch the function and the tangent line, then take the first derivative to find the equation for the slope. Enter the x value of the point you’re investigating into the function, and write the equation in point-slope form. Check your answer by confirming the equation on your graph. For examples of tangent line equations, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,184,568 times.
Did this article help you?
Cправочник репетитора по математике предназначен для учащихся 5-11 классов и для преподавателей математики. Последние найдут в нем несколько оригинальных подходов к подаче и оформлению теоретических конспектов, упрощающих работу школьников с математическими понятиями и законами.
Касательная к графику функции.
Школьное определение касaтельной: прямая y=f (x) называется касательной к графику функции f (x) в точке  если она проходит через точку
если она проходит через точку  и имеет угловой коэффициент
и имеет угловой коэффициент  .
.
Строгое определение касательной (из курса математического анализа) : прямая  называется касательной к графику функции
называется касательной к графику функции  в точке
в точке  , если при
, если при  разность
разность  есть бесконечно малая величина, более высокого порядка малости чем
есть бесконечно малая величина, более высокого порядка малости чем 
Иллюстрация касательной m к графику функции  в точке
в точке  :
:

Геометрический смысл производной: Значение производной функции  в точке
в точке  равнo угловому коэффициенту касательной, проведенной к
равнo угловому коэффициенту касательной, проведенной к  в точке
в точке  , то есть
, то есть  , где k — угловой коэффициент касательной.
, где k — угловой коэффициент касательной.
Комментарий репетитора по математике: угол наклона касательной определяется как направленный положительный угол, то есть тот самый угол, который вы привыкли откладывать на тригонометрическом круге от положительного направления оси OX против часовой стрелки. Поэтому, если если касательная отклонена влево от вертикального положения, ваш угол наклона окажется тупым, то есть принадлежащим промежутку ![[0;pi] [0;pi]](https://ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_81caf8e5ffcc03c07b3aa0041092b867.png) . Так как тангенс любого такого угла (угла второй четверти) отрицательный, то отрицательной окажется и производная.
. Так как тангенс любого такого угла (угла второй четверти) отрицательный, то отрицательной окажется и производная.
Общая форма уравнения касательной: 
Окончательная форма уравнения касательной :

Полезные факты для решения задач на касательную:
1) две наклонный прямые параллельны, тогда и только тогда, когда их угловые коэффициенты равны.
2) две наклонный прямые перпендикулярны тогда и только тогда, когда произведение их угловых коэффициентов равно -1.
Как найти угол наклона касательной по ее угловому коэффициенту:
Если  , то
, то 
Если  , то
, то 
Достаточный признак возрастания функции: если все значения производной некоторой функции положительны внутри промежутка, то функция внутри него строго возрастает.
Замечание репетитора по математике: если концы промежутка являются точками непрерывности функции (один или оба), то их можно присоденить к указанному промежутку возрастания.
Достаточный признак убывания функции: если все значения производной некоторой функции отрицательны внутри промежутка, то функция внутри него строго убывает.
Замечание репетитора по математике: если функция непрерывна на концах промежутка (на одном или на обоих), то эти концы можно присоединить к указанному промежутку убывания.
Блиц вопросы к репетитору:
Что такое критическая точка? Внутренняя точка области определения функции называется критической, если производная в этой точке либо не сущуствует, либо она равна нулю.
Что такое стационарная точка: Если у критической точки производная равна нулю — она называется стационарной точной.
Экстремумы
Минимум функции.
Определение: Точка  называется точкой минимума функции
называется точкой минимума функции  , если в некотором промежутке I оси ОХ, содержащем
, если в некотором промежутке I оси ОХ, содержащем  для всех точек
для всех точек  выполняется неравенство
выполняется неравенство  . В этом случае число
. В этом случае число  называется минимумом функции в точке
называется минимумом функции в точке  (или локальным минимумом).
(или локальным минимумом).
Фрагмент графика функции, имеющей точку минимума:

Комментарий репетитора по математики к рисунку: знаки — и + на оси OХ показывают на отрицательные/положитлеьные значения производной в левой/правой окрестности точки  . Стрелки указывают на возрастание и убывание функции в этих крестностях. Я советую репетиторам математики включать в теоретические памятки для учеником именно такую (интегрированную) иллюстрацию минимума.
. Стрелки указывают на возрастание и убывание функции в этих крестностях. Я советую репетиторам математики включать в теоретические памятки для учеником именно такую (интегрированную) иллюстрацию минимума.
Максимум функции.
Определение:Точка  называется точкой максимума функции
называется точкой максимума функции  , если в некотором промежутке I оси ОХ, содержащем
, если в некотором промежутке I оси ОХ, содержащем  для всех точек
для всех точек  выполняется неравенство
выполняется неравенство  . В этом случае число
. В этом случае число  называется максимумом функции в точке
называется максимумом функции в точке  (или локальным максимумом).
(или локальным максимумом).
Фрагмент графика функции, имеющей точку максимума:

Комментарий репетитора по математике: все обозначения и опорные знаки для подачи материала преподавателем аналогичны случаю с минимумом.
Экстремум – общее название минимума и максимума. Точка экстремума – общее название для точки минимума и точки максимума. На всех рисунках  — экстремум, а
— экстремум, а  — точка экстремума.
— точка экстремума.
Необходимое условие существования экстремума: если  — точка экстремума и в этой точке существует производная, то она равна нулю, то есть
— точка экстремума и в этой точке существует производная, то она равна нулю, то есть  . В этом случае касательная, проведенная к графику функции будет параллельна оси ОХ.
. В этом случае касательная, проведенная к графику функции будет параллельна оси ОХ.
Достаточное условие существования экстремума: если функция y=f (x) непрерывна в точке  и при переходе через
и при переходе через  производная меняет знак , то
производная меняет знак , то  — точка экстремума.
— точка экстремума.
Признак минимума функции: если функция y=f (x) непрерывна в точке  и производная меняет знак с минуса на плюс, то
и производная меняет знак с минуса на плюс, то  — точка минимума.
— точка минимума.

Признак максимума функции: если функция y=f (x) непрерывна в точке  и производная меняет знак с плюса на минус , то
и производная меняет знак с плюса на минус , то  — точка максимума.
— точка максимума.

Алгоритм нахождения наибольшего и наименьшего значения функции y=f (x) на отрезке [a;b], на которм она непрерывна
1) Найдите производную  от данной функции
от данной функции
2) Найдите стационарные точки, решив уравнение 
2*) В редких случаях функция может иметь точки, в которых производной не существует. Их тоже нужно выявить.
3) Выберите из всех найденных точек те, которые попадают в исследуемый отрезок
4) Найдите значения данной функции в выбранных точках
5) Выберите среди них наименьшее и наибольшее
План исследования функции с применением производной. Построение графика.
1) Найдите производную 
2) Разложите ее на множители (если это возможно) или приведите все ее дроби к общему знаменателю, а затем разложите числитель. Тем самым вы ее готовите к дальнейшему исследованию методом интервалов
2) Определите у функции критические и стационарные точки, приравнивая числитель и знаменатель ее производной к нулю
2*) Точки, в которых производной не существует (обычно это нули знаменателя) отесите в группу тех, в которых функция будет иметь вертикальные асимптоты
3) Отметьте все найденные точки на оси Х и раставьте методом интервалов на образовавшихся промежутках знаки производной
4) Определите промежутки монотонности (промежутки возрастания и убывания) и над каждым из них поставьте соответствующую стрелку в соответствии с видом этой монотонности
5) Определите через признак минимума и максимума (или по характеру расположения стрелок) соответствующие точки экстремумов и найдите значения функции в этих точках
6) Нанесите их на координатной плоскости и также по характеру стрелок проведите через эти точки график.
Замечание репетитора по математике: аккуратнее выполняйте рисунок вблизи асимптот. График функции не должен их пересекать и обрываться рядом с ними. Плавно приближайте его к асимтоте пока на это хватает выделенного пространства системы координат.
Удачи в изучении математики!
Колпаков Александр Николаевич, репетитор по математике, Москва, Строгино.
Виртуальный математический справочник профессионального репетитора — преподавателя.
