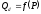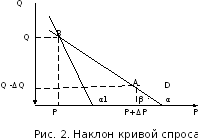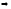Спрос
(D
– demand)
на какой-либо товар характеризует
количество продукта, которое потребители
желают, готовы и в состоянии купить по
одной из возможных в течение определенного
периода времени цене.
Функция
спроса
представляет
зависимость объема спроса от влияющих
на него факторов – независимых
экономических переменных. Прежде всего,
спрос зависит от цены
(price)
данного товара. На спрос оказывают
влияние неценовые факторы. Среди них
– цены на другие товары;
(income)
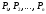
– доходы потребителей;
– вкусы, потребительские предпочтения;
(wait)
– ожидания;
(number)
– количество покупателей;
– прочие факторы.
Функция
спроса в неявном виде:
,
где
(quantity)
–
объем
спроса на товар, показывает количество
этого товара, которое желает купить
отдельный потребитель, группа потребителей
или все общество в целом в единицу
времени при определенных условиях.
Функция спроса является функцией многих
переменных.
Кривая
спроса
показывает,
какое количество товара готовы купить
покупатели по разным ценам в данный
момент времени.
В
экономической теории принято, следуя
традиции А. Маршалла, откладывать
независимую переменную (
)
по вертикальной оси – оси ординат, а
зависимую (
)
– по горизонтальной оси – оси абсцисс.
Математики поступают иначе: на оси
ординат откладывают значения зависимой
переменной, на оси абсцисс – независимой
переменной.
Точка
на кривой спроса характеризует уровень
цены и объем покупок товара в определенный
момент времени. Она имеет отрицательный
наклон, что свидетельствует о желании
потребителей купить большее количество
благ при меньшей цене.
Если
неценовые факторы спроса не изменяются
(постоянны), то объем спроса зависит
только от цены товара, от одной переменной:
На
графике изменение цены вызывает
изменение объема спроса и перемещение
из одной точки кривой спроса (точки
)
в другую (точку
)
при снижении цены с
до
,
и в обратном направлении при повышении
цены (рис 1а).
При
изменении неценовых факторов происходит
изменение самого спроса, или изменение
в самом спросе, которое сдвигает кривую
спроса вправо вверх при увеличении
спроса или влево вниз при сокращении
спроса (рис. 1 б).
Примером
простейших функций спроса в явном виде
являются линейная функция
,
где
– константы, имеющие экономический смысл
и различающиеся у каждого товара и в
различные периоды времени; степенная
функция спроса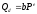
была характерна для ряда товаров
потребительского спроса в 30-40 гг.XIX
в. Здесь
–
коэффициент ценовой эластичности
спроса.
1.2. Наклон кривой спроса для нормальных товаров.
Задана
некоторая функция спроса
и графически представлена на рис. 2.
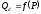
Исходная точка
с координатами
.
Допустим, цена
растет, спрос уменьшается и новая
ситуация представлена точкой
с координатами
.
Наклон
кривой спроса на дуге
определяется наклоном секущей линии,
проведенной через точки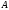
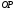
и
к оси
,
и измеряется отношением изменения
объема спроса к вызвавшему его изменению
цены:
.
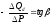
Секущая
образует угол
с отрицательно направленной осью
.
Экономисты же измеряют наклон кривых
тангенсом угла, который образуют секущая
(на дуге) или касательная (в точке) только
с положительно направленной осью
абсцисс. Поэтому наклон кривой спроса
измеряют тангенсом угла
,
т.е.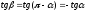
.
Следовательно, кривая спроса для
нормальных товаров имеет отрицательный
наклон.
Если
задана функция спроса, то наклон кривой
в точке определяется первой производной.
Так, если
,
то точка
пробежит по дуге в направлении к точке
и совпадет с ней. Секущая линия повернется
и займет положение касательной к кривой
спроса в точке
.
Тогда наклон кривой спроса в точке будет
равен тангенсу угла, который образует
касательная в этой точке с положительно
направленной осью
.
Если
,
то
.
Наклон кривой спроса в точке равен
.
Если
функция спроса линейна, то ее наклон
измеряется угловым коэффициентом (-
).
Наклон кривой спроса для нормальных
товаров отрицательный. Это означает,
что между объемом спроса на товар и его
ценой существует обратная зависимость
(
).
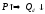
Предложение
(S
– supply)
характеризует
количество продукта, которое производитель
желает и может произвести, продать на
рынке по сложившейся на рынке цене в
течение определенного периода времени.
Функция
предложения характеризует зависимость
объема предложения
от
влияющих на него различных факторов.
На предложение оказывают влияние
следующие факторы:
– цена данного товара; неценовые факторы,
к которым относятся
– цены на другие товары;
– цены на ресурсы;
(tax)
– налоги;
(subsidy)
– субсидии;
– прочие факторы.
Функция
предложения в неявном виде:
,
где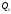
–
объем предложения товара.
Если
все неценовые факторы предложения не
изменяются, постоянны, то функция
предложения в
неявном
виде может быть представлена следующим
образом:
.
Каждая точка на кривой предложения
представляет, какое количество товара
готовы продать производители по разным
ценам в данный момент времени.
Аналогично,
как и в случае кривой спроса, для кривой
предложения на графике изменение цены
выражается в изменении объема предложения
и движении вдоль кривой предложения из
одной точки в другую: вверх по кривой
предложения в случае роста цены и вниз
в случае снижения цены. Изменение
неценовых факторов вызывает сдвиг
кривой предложения. Так, введение налога
с продаж передвигает кривую предложения
влево и вверх.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Overall, there are many factors that influence supply. In an ideal world, economists would have a good way to graph supply versus all of these factors at once.
Price Versus Quantity Supplied
In reality, however, economists are pretty much limited to two-dimensional diagrams, so they have to choose one determinant of supply to graph against quantity supplied. Luckily, economists generally agree that the price of a firm’s output is the most fundamental determinant of supply. In other words, price is likely the most important thing that firms consider when they are deciding whether they are going to produce and sell something. Therefore, the supply curve shows the relationship between price and quantity supplied.
In mathematics, the quantity on the y-axis (vertical axis) is referred to as the dependent variable and the quantity on the x-axis is referred to as the independent variable. However, the placement of price and quantity on the axes is somewhat arbitrary, and it should not be inferred that either of them is a dependent variable in a strict sense.
This site uses the convention that a lowercase q is used to denote individual firm supply and an uppercase Q is used to denote market supply. This convention isn’t universally followed, so it’s important to always check whether you are looking at individual firm supply or market supply.
The Law of Supply
The law of supply states that all else being equal, the quantity supplied of an item increases as the price increases, and vice versa. The “all else being equal” part is important here, since it means that input prices, technology, expectations, and so on are all held constant and only the price is changing.
The vast majority of goods and services obey the law of supply, if for no other reason than it’s more attractive to produce and sell an item when it can be sold at a higher price. Graphically, this means that the supply curve usually has a positive slope, i.e. slopes up and to the right. The supply curve doesn’t have to be a straight line but like the demand curve, it’s usually drawn that way for simplicity.
Start by plotting the points in the supply schedule on the left. The rest of the supply curve can be formed by plotting the applicable price/quantity pairs at every possible price point.
How to Find the Slope of the Market Supply Curve
Since slope is defined as the change in the variable on the y-axis divided by the change in the variable on the x-axis, the slope of the supply curve equals the change in price divided by the change in quantity. Between the two points labeled above, the slope is (6-4)/(6-3), or 2/3. Note that the slope is positive, as the curve slopes up and right.
Since this supply curve is a straight line, the slope of the curve is the same at all points.
A Change in Quantity Supplied
A movement from one point to another along the same supply curve, as illustrated above, is referred to as a “change in quantity supplied.” Changes in quantity supplied are due to changes in price.
The Supply Curve Equation
The supply curve can be written algebraically. The convention is for the supply curve to be written as quantity supplied as a function of price. The inverse supply curve, on the other hand, is the price as a function of quantity supplied.
The equations above correspond to the supply curve shown earlier. When given an equation for a supply curve, the easiest way to plot it is to focus on the point that intersects the price axis. The point on the price axis is where the quantity demanded equals zero, or where 0=-3+(3/2)P. This occurs where P equals 2. Because this supply curve is a straight line, you can just plot one other random price/quantity pair and then connect the points.
You will most often work with the regular supply curve, but there are a few scenarios where the inverse supply curve is very helpful. Luckily, it is fairly straightforward to switch between the supply curve and the inverse supply curve by solving algebraically for the desired variable.
Sources
“x-axis.” Dictionary.com, LLC, 2019.
“y-axis.” Dictionary.com, LLC, 2019.
Перейти к содержанию
Понимание того, как работает кривая предложения
На чтение 4 мин. Просмотров 50 Опубликовано 07.06.2021
В целом на предложение влияет множество факторов. В идеальном мире у экономистов был бы хороший способ построить график зависимости предложения от всех этих факторов одновременно.
Содержание
- Цена по сравнению с поставленным количеством
- Закон предложения
- Кривая предложения
- Как найти наклон Кривая рыночного предложения
- Изменение поставляемого количества
- Уравнение кривой предложения
Цена по сравнению с поставленным количеством
На самом деле, однако, экономисты в значительной степени ограничены двумерными диаграммами, поэтому у них есть выбрать один определяющий фактор предложения для построения графика в зависимости от поставленного количества. К счастью, экономисты в целом согласны с тем, что цена продукции фирмы является наиболее фундаментальным фактором, определяющим предложение. Другими словами, цена, вероятно, является наиболее важным фактором, который фирмы принимают во внимание при принятии решения о том, собираются ли они что-то производить или продавать. Следовательно, кривая предложения показывает взаимосвязь между ценой и объемом предложения.
В математике количество на оси Y (вертикальная ось) называется зависимой переменной, а количество на оси x -axis называется независимой переменной. Однако размещение цены и количества на осях несколько произвольно, и не следует делать вывод, что какая-либо из них является зависимой переменной в строгом смысле.
На этом сайте используется соглашение о том, что Строчная буква q используется для обозначения предложения отдельных фирм, а заглавная буква Q используется для обозначения рыночного предложения. Это соглашение не соблюдается повсеместно, поэтому важно всегда проверять, смотрите ли вы на предложение отдельной фирмы или предложение на рынке.
Закон предложения
Закон предложения гласит, что при прочих равных, поставляемое количество товара увеличивается с ростом цены, и наоборот. Здесь важна часть «при прочих равных», поскольку это означает, что цены на ресурсы, технологии, ожидания и т. Д. Остаются неизменными, и меняется только цена.
Подавляющее большинство из них. товары и услуги подчиняются закону предложения, хотя бы по той причине, что производить и продавать товар более привлекательно, если он может быть продан по более высокой цене. Графически это означает, что кривая предложения обычно имеет положительный наклон, то есть наклон вверх и вправо. Кривая предложения не обязательно должна быть прямой, но, как и кривая спроса, ее обычно рисуют таким образом для простоты.
Кривая предложения
Начните с нанесения точек в график снабжения слева. Остальная часть кривой предложения может быть сформирована путем построения соответствующих пар цена/количество во всех возможных ценовых точках..
Как найти наклон Кривая рыночного предложения
Поскольку наклон определяется как изменение переменной на оси y, деленное на изменение переменной на оси x, наклон кривой предложения равен изменению цены, деленному на изменение количества. Между двумя точками, отмеченными выше, наклон равен (6-4)/(6-3) или 2/3. Обратите внимание, что наклон положительный, так как кривая наклоняется вверх и вправо.
Поскольку эта кривая предложения является прямой линией, наклон кривой одинаков во всех точках.
Изменение поставляемого количества
Движение от одной точки к другой по той же кривой предложения, как показано выше, называется «изменением объема предложения». Изменения в поставленном количестве связаны с изменением цены.
Уравнение кривой предложения
Кривую предложения можно записать алгебраически. Согласно соглашению, кривая предложения записывается как количество поставляемого продукта как функция цены. С другой стороны, обратная кривая предложения – это цена как функция от количества предложения.
Приведенные выше уравнения соответствуют кривой предложения, показанной ранее. Когда дано уравнение для кривой предложения, самый простой способ построить его – это сосредоточиться на точке, которая пересекает ось цены. Точка на оси цен – это точка, где объем спроса равен нулю или где 0 = -3 + (3/2) P. Это происходит, когда P равно 2. Поскольку эта кривая предложения представляет собой прямую линию, вы можете просто построить еще одну случайную пару цена/количество, а затем соединить точки.
Чаще всего вы будете работать с обычным кривая предложения, но есть несколько сценариев, в которых обратная кривая предложения очень полезна. К счастью, довольно просто переключиться между кривой предложения и обратной кривой предложения, решив алгебраически для желаемой переменной.
Источники
“ось x”. Dictionary.com, LLC, 2019.
«ось Y». Dictionary.com, LLC, 2019.
|
|
|
|||
|
|||||
|
–
|
