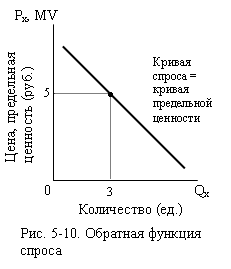
5.4. Обратная функция спроса
В микроэкономическом
анализе часто используется обратная функция спроса. В этом случае цена представляется как функция величины спроса: Р = g(Q). Преобразовать обычную, прямую
функцию спроса в обратную очень просто. Предположим дана функция : Q = 13 – 2Р. Обратная функция спроса тогда будет: Р = 6,5 – 0,5Q. На графике обратная функция спроса выглядит точно так же как прямая функция (рис. 5-10). Обратная
функция спроса показывает какой должна быть рыночная цена товара Р, для того чтобы спрос на него составил Q единиц. В то же время было бы ошибкой считать, что это функция говорит о том, что величина спроса определяет рыночную цену. Каков же тогда экономический смысл обратной функции спроса?
Мы уже доказывали, что кривая индивидуального спроса
совпадает с кривой предельной ценности. Потребитель будет увеличивать
потребление блага до тех пор, пока не достигнет точки в которой предельная
ценность единицы блага равна его цене. Так на рис. 5-10, если рыночная цена
блага Х равна 5 рублям, и предельная ценность для потребителя 1-й, 2-й и 3-й
единиц блага составляют соответственно 6, 5,5 и 5 руб., то он приобретёт три
единицы. Так как он будет делать это при любой заданной цене, то график того,
сколько он будет покупать при любой цене – то же самое, что график предельной
ценности (MV). Но предельная ценность единицы блага
зависит от количества потребляемого блага. Следовательно, обратная функция спроса – это, по сути, функция предельной ценности. Она
отражает то обстоятельство, что с увеличением количества потребляемого блага
предельная полезность, а следовательно и предельная ценность блага для
потребителя падает. Ранее мы установили также, что высота кривой спроса в любой
её точке равна предельной норме замещения. Следовательно, обратная функция
спроса показывает предельную норму замещения, или предельную готовность
потребителя платить за товар, или предельную ценность товара для потребителя.
Всё это суть одно и то же.
Суммирование
обратных функций индивидуального спроса отличается от суммирования прямых
функций спроса и по смыслу и технически. Агрегированная обратная функция спроса
показывает какова общая для всех потребителей (суммарная) ценность каждой
единицы блага. Здесь уже складываются не количества блага, а предельные
ценности. Поэтому сложение обратных функций индивидуального спроса нужно
производить по вертикали, а не по горизонтали. Эта операция будет иметь
экономический смысл в том случае, если благо потребляется индивидами совместно.
Такие экономические блага существуют и называются общественными благами.
Обратная функция спроса нам очень пригодится в теории общественных благ,
которую мы рассмотрим в конце курса.
Обратная функция спроса — вариант функции спроса, которая рассматривает цену товара как функцию от количества[1][2]:
Функция спроса выражает зависимость объёма реализации от цены (
Обратная функция спроса идентична функции средней выручки, где P = AR.[4]
Для того, чтобы найти обратную функцию спроса, необходимо решить уравнение спроса для P. Так, если функция спроса имеет форму 

Практическое применение[править | править код]
Обратная функция спроса используется для выведения функций общего и предельного доходов. Общий доход равен цене товара P, умноженной на количество Q, или TR = P×Q, где TR — общий доход (от англ. total revenue). Для выведения функции общего дохода необходимо просто умножить обратную функцию на Q. Из вышеприведенного примере имеем: 

К примеру, допустим функция издержек имеет вид 

Обратная функция спроса является той формой функции спроса, которая используется в Кресте Маршалла (ножницах Маршалла). Функция изображается в такой форме, поскольку независимая переменная располагается на оси y, а зависимая переменная — на оси x. Наклонная обратной функции тогда является ∆P/∆Q. Именно это необходимо учитывать при расчете эластичности, которая рассчитывается по формуле (∆Q/∆P) × (P/Q).
Взаимосвязь с предельным доходом[править | править код]
Существует тесная связь между любой обратной функцией спроса линейной формы и функцией предельного дохода. Для любой обратной функции спроса линейной формы вида P = a — bQ, функция предельного дохода имеет форму MR = a — 2bQ.[7] Функция предельного дохода и обратная функция спроса линейной формы имеют следующие свойства:
- Обе функции линейны.[8]
- Обе функции имеют одну и ту же точку пересечения с осью y.[7]
- Значение точки пересечения с осью x у функции предельного дохода вдвое меньше точки пересечения обратной функции спроса.
- Наклонная у функции предельного дохода вдвое больше наклонной обратной функции спроса.[7]
- Функция предельного дохода всегда ниже обратной функции спроса для любого положительного объема.[9]
См. также[править | править код]
- Спрос и предложение
- Спрос
- Закон спроса
- Экономическая прибыль
- Предельный доход
- Предельные издержки
- Общие затраты
Примечания[править | править код]
- ↑ R., Varian, Hal. Intermediate microeconomics : with calculus. — First. — New York, 7 April 2014. — P. 115. — ISBN 9780393123982.
- ↑ Samuelson, W and Marks, S Managerial Economics 4th ed. page 35. Wiley 2003.
- ↑ Varian, H.R (2006) Intermediate Microeconomics, Seventh Edition, W.W Norton & Company: London
- ↑ Chiang & Wainwright, Fundamental Methods of Mathematical Economics 4th ed. Page 172. McGraw-Hill 2005
- ↑ Samuelson & Marks, Managerial Economics 4th ed. (Wiley 2003)
- ↑ Perloff, Microeconomics, Theory & Applications with Calculus (Pearson 2008) 240.ISBN 0-321-27794-5
- ↑ 1 2 3 Samuelson, W & Marks, S Managerial Economics 4th ed. Page 47. Wiley 2003.
- ↑ Perloff, J: Microeconomics Theory & Applications with Calculus page 363. Pearson 2008.
- ↑ Perloff, J: Microeconomics Theory & Applications with Calculus page 362. Pearson 2008.
Если предположить, что
p280
и m
неизменны, и отложить на графике р181
по вертикальной оси и
x182
по горизонтальной, то получим кривую
спроса. Как
сказано выше, обычно мы полагаем, что
кривая спроса нисходящая, так что более
высоким ценам соответствует меньший
спрос, хотя пример товара Гиффена
показывает, что дело может обстоять и
по-другому.
До тех пор, пока мы
действительно имеем дело с нисходящей
кривой спроса, что типично, имеет смысл
говорить об обратной
функции спроса.
Это такая функция спроса, в которой цена
выступает функцией количества. Иными
словами, для каждого данного уровня
спроса на товар 1 обратная функция спроса
показывает, какова должна быть цена
товара 1, чтобы потребитель выбрал данный
объем потребления. Таким образом,
обратная функция спроса количественно
выражает ту же самую взаимозависимость,
что и прямая, но с другой точки зрения.
На рис. 6.15 изображена обратная функция
спроса — или же прямая функция спроса,
в зависимости от того, как на нее
посмотреть.
Вспомним, например,
функцию спроса Кобба — Дугласа
на товар 1,
x1
= = am/p183.
Можно с тем же успехом записать эту
взаимосвязь между ценой и величиной
спроса как p1
= am/x184.
Первый способ представления данной
взаимосвязи есть прямая функция спроса,
второй способ представления — обратная
функция спроса.
У обратной функции
спроса имеется полезная экономическая
интерпретация. Вспомним, что до тех пор,
пока оба товара потребляются в
положительных количествах, оптимальный
выбор должен удовлетворять тому условию,
что абсолютная величина MRS равна отношению
цен:
85.
Это говорит о том, что
при оптимальном объеме спроса на товар
1, например, должно соблюдаться равенство
p1
= p2|MRS|.
(6.4)
Таким образом, при
оптимальном объеме спроса на товар 1
цена товара 1 пропорциональна абсолютной
величине предельной нормы замещения
товара 2 товаром 1.
|
Рис. 6.15 |
Обратная |
Предположим для
простоты, что цена товара 2 равна единице.
Тогда уравнение (6.4) говорит нам о том,
что при оптимальном объеме спроса цена
товара 1 показывает, сколько товара 2
готов отдать потребитель, чтобы получить
немного больше товара 1. В этом случае
обратная функция спроса количественно
выражает просто абсолютную величину
MRS. Обратная кривая спроса говорит о
том, сколько товара 2 потребитель хотел
бы получить, чтобы при любом оптимальном
объеме х187
компенсировать малое сокращение
потребляемого количества товара 1. Или,
напротив, обратная кривая спроса
показывает, сколько товара 2 готов
уступить потребитель, чтобы ему стало
безразлично, получит он взамен немного
больше товара 1 или нет.
Если считать, что товар
2 — деньги, расходуемые на все другие
товары, то MRS можно трактовать просто
как то количество долларов, которое
индивид готов уступить, чтобы получить
взамен чуть больше товара 1. Ранее мы
предположили, что в этом случае можно
рассматривать MRS просто как меру
предельной готовности платить. Поскольку
цена товара 1 в этом случае есть не что
иное, как MRS, это означает, что сама цена
товара 1 измеряет предельную готовность
платить.
При любом количестве
х188
обратная кривая спроса показывает то
количество долларов, которое потребитель
готов уступить, чтобы получить чуть
больше товара 1; или, другими словами,
она показывает то количество долларов,
которое потребитель готов был бы отдать
за последнюю покупаемую единицу товара
1. Для достаточно малого количества
товара 1 эти утверждения сводятся к
одному и тому же.
Если посмотреть на
нисходящую кривую спроса с данной точки
зрения, то она приобретает новый смысл.
Когда количество х189
очень мало, потребитель готов отдать
много денег, т. е. много других товаров,
чтобы приобрести чуть больше товара 1.
По мере возрастания x190,
потребитель готов отдать все меньше
денег, чтобы в пределе приобрести чуть
больше товара 1. Следовательно, предельная
готовность платить, в смысле предельной
готовности пожертвовать товаром 2 ради
приобретения товара 1, при увеличении
потребления товара 1 убывает.
Краткие
выводы
-
Функция спроса
потребителя на товар в общем случае
зависит от цен всех товаров и от дохода. -
Нормальный товар —
это такой товар, спрос на который с
ростом дохода увеличивается. Товар
низшей категории — такой товар, спрос
на который с ростом дохода уменьшается. -
Обычный товар — это
товар, спрос на который с ростом цены
умень-шается. Товар Гиффена — товар,
спрос на который с ростом цены
увели-чивается. -
Если спрос на товар 1
при росте цены товара 2 возрастает, то
товар 1 является субститутом товара 2.
Если спрос на товар 1 в этой ситуации
сокращается, то товар 1 является для
товара 2 комплементом. -
Обратная функция
спроса показывает цену, при которой
возникает спрос на данное количество
товара. Высота кривой спроса при данном
объеме потребления показывает предельную
готовность заплатить за добавочную
единицу товара при этом объеме
потребления.
ВОПРОСЫ
ДЛЯ ПОВТОРЕНИЯ
-
Если потребитель
потребляет только два товара и всегда
тратит на них весь свой доход, то могут
ли оба этих товара быть товарами низшей
категории? -
Покажите, что совершенные
субституты являют собой пример
гомотетич-ных предпочтений. -
Покажите, что предпочтения
Кобба — Дугласа гомотетичны. -
Кривая “доход — потребление”
для кривой Энгеля то же, что кривая
“це-на — потребление” для…? -
Если предпочтения
описываются кривыми безразличия,
выпуклыми от начала координат, то может
ли потребитель потреблять оба товара
вместе? -
Каков вид обратной
функции спроса на товар 1 в случае
совершенных комплементов?
ПРИЛОЖЕНИЕ
Если
предпочтения имеют особый вид, это
означает, что и функции спроса, возникающие
на основе этих предпочтений, также
принимают особый вид. В гл. 4 описаны
квазилинейные предпочтения. Эти
предпочтения предполагают существование
кривых безразличия, параллельных между
собой, и могут быть представлены функцией
полезности вида
u(x1,
x2)
= v(x1)
+ x291.
Задача
на нахождение максимума подобной функции
полезности принимает вид
max v(x1)
+ x292
x1,
x293
при
p1x1
+ p2x2
= m94.
Выразив
из бюджетного ограничения х2
как
функцию от х195
и подставив результат в целевую функцию,
получаем
max v(x1)
+ m/p2
— p1x1/p296.
x197
Взяв
производную данного выражения, получаем
условие первого порядка
98.
Эта
функция спроса обладает интересным
свойством — спрос на товар 1 должен быть
независим от дохода, что мы уже видели
при использовании кривых безразличия.
Обратная кривая спроса дана уравнением
p1(x1)
= v’(x1)p299.
Иными
словами, обратная кривая спроса на товар
1 есть производная функции полезности,
умноженная на p2100.
Стоит нам узнать функцию спроса на товар
1, и функция спроса на товар 2 может быть
найдена из бюджетного ограничения.
Например,
рассчитаем функции спроса для функции
полезности вида
u(x1,
x2)
= ln x1
+ x2101.
Применение
условия первого порядка дает
102,
так
что прямая функция спроса на товар 1
есть
103,
а
обратная функция спроса есть
104.
Прямую
функцию спроса на товар 2 находим
подстановкой
105
в бюджетное ограничение:
—1106.
Необходимо
сделать одно предостережение в отношении
указанных функций спроса. Обратите
внимание на то, что в рассматриваемом
примере спрос на товар 1 независим от
дохода. Это общее свойство, присущее
квазилинейным функциям полезности: при
изменении дохода спрос на товар 1 остается
постоянным. Однако данное утверждение
верно лишь для некоторых значений
дохода. Функция спроса не может быть в
буквальном смысле независимой от дохода
для всех
его значений; скажем, когда доход равен
нулю, спрос тоже равен нулю. Выведенная
выше квазилинейная функция спроса имеет
смысл только при потреблении положительных
количеств каждого товара. При низких
уровнях дохода функция спроса принимает
несколько иной вид. См. рассуждения по
поводу квазилинейных функций спроса в
кн. Hal R.Varian, Microeconomic
Analysis,
3rd ed. (New York: Norton, 1992).
1
Термин “резервная
цена” обязан своим происхождением
аукционной торговле. Желающий продать
что-то на аукционе обычно объявлял
минимальную цену, по которой готов был
продать товар. Если лучшая предложенная
цена была лучше этой объявленной цены,
продавец резервировал за собой право
купить товар самому. Указанная цена
получила название “резервной цены
продавца” и со временем стала
применяться для обозначения цены, по
которой кто-то просто хочет купить или
продать некий товар.
Соседние файлы в папке Вэриан_Микроэкономика Промежуточный уровень
- #
- #
- #
- #
09.05.2015424.96 Кб10G4.DOC
- #
09.05.2015728.58 Кб8G5.DOC
- #
- #
09.05.2015556.54 Кб10G7.DOC
- #
- #
09.05.2015860.16 Кб9G9.DOC
- #
- #
Содержание
- Множественный регрессионный анализ
- Обратная функция спроса
- Примеры и графики
Функция спроса – это математическое уравнение, которое выражает спрос на продукт или услугу в зависимости от его цены и других факторов, таких как цены на заменители и дополнительные товары, доход и так далее.
Функция спроса создает связь между спросом (требуемым количеством) на продукт (который является зависимой переменной) и факторами, влияющими на спрос, такими как цена продукта, цена замещающих и дополняющих товаров, средний доход и прочие (которые являются независимыми переменными).
Давайте рассмотрим рынок приложений для найма автомобиля с водителем и выясним факторы, которые могут повлиять на ежедневный пробег таксистов, предлагающих данный вид услуги.
Множественный регрессионный анализ
Самым важным фактором является стоимость проезда (цена, взимаемая за километр пути).
Другие потенциальные факторы являются детерминантами спроса, включая цену заменителей, то есть цену общественного транспорта или конкурирующих услуг такси независимо от того, рабочий или выходной день, ясная или дождливая погода и так далее.
Один из методов создания функции спроса заключается в использовании множественного регрессионного анализа для выяснения взаимосвязи между требуемым количеством, ценой продукта и всеми другими факторами.
Множественный регрессионный анализ присваивает различные коэффициенты каждому из факторов, влияющих на спрос. Знак коэффициента – положительный или отрицательный – говорит нам, связаны ли спрос и фактор положительно или отрицательно.
Предположим для упрощения, что вы использовали только две переменные – (1) цену самого продукта и (2) рост цены конкурирующего общественного транспорта – и пришли к следующему уравнению:
Q = 1,200,000 – 150,000 × P + 200,000 × PPT, где
Q – это потребляемые километры,
P – цена за километр услуги по вызову пассажиров,
PPT – увеличение цены за поездку в системе общественного транспорта.
Параметр Р имеет отрицательный знак, который показывает, что с каждым долларовым увеличением стоимости проезда за километр требуемое количество будет уменьшаться на 150 000 километров в день.
С другой стороны, параметр PPT имеет положительный знак, а это означает, что увеличение платы за проезд в общественном транспорте на один доллар приведет к увеличению спроса на 200 000 километров.
Поскольку приведенное выше уравнение создает связь не только между требуемыми километрами и взимаемой ценой, но и с ценой заменителя, оно представляет собой как сдвиг кривой спроса, так и движение вдоль кривой спроса.
До тех пор, пока цены на общественный транспорт не изменятся, мы можем упростить функцию спроса до соотношения между Q и P:
Q = 1,200,000 – 150,000 × P
Мы можем разработать график спроса, используя приведенное выше уравнение, просто подключив различные цены за километр.
Обратная функция спроса
График спроса и предложения обычно строится таким образом, что количество находится на оси X, а цена – на оси Y, но функция спроса, которую мы определили выше, имеет цену (P) как независимую переменную и количество (Q) как независимую переменную.
Функция спроса иногда определяется ценой P как независимой переменной. Такая функция спроса называется обратной функцией спроса.
С помощью всего лишь нескольких математических манипуляций мы можем преобразовать функцию спроса, определенную выше, в обратную функцию спроса:
150,000 × P = 1,200,000 – Q
P = (1,200,000 – Q) / 150,000
P = 8 – Q / 150,000
Обратная функция спроса полезна, когда мы заинтересованы в поиске предельного дохода, дополнительного дохода, полученного от одной проданной дополнительной единицы.
Функция предельного дохода является первой производной от обратной функции спроса. Для обратной функции спроса вида P = a – bQ функция предельного дохода равна MR = a – 2bQ. Функция предельного дохода в данном случае выглядит следующим образом:
P = 8 – 2 × Q / 150,000 = 8 – Q / 75,000
Примеры и графики
Давайте выясним, каков объем перевозок в километрах будет востребован при следующих сценариях: (A) средняя цена за километр (Р) составляет $ 1.5 и $ 1.75; и (B) средняя цена за километр (Р) составляет $ 1.5, а рост цен на общественный транспорт (РРТ) – $ 0.25
Сценарий А
Следующее уравнение показывает требуемое количество, соответствующее каждой цене:
Q1.50 = 1,200,000 – 150,000 × $ 1.50 = 975,000
Q1.75 = 1,200,000 – 150,000 × $ 1.75 = 937,500
Сценарий В
В этом случае происходит изменение цены заменителя, поэтому она представляет собой сдвиг кривой:
Q1.50;0.25 = 1,200,000 – 150,000 × $ 1.50 + 200,000 × $ 0.25 = 1,025,000
В нашем примере Q1.50;0.25 выше, чем Q1.50, потому что рост цен на общественный транспорт вызвал внешний сдвиг кривой спроса.
На следующей диаграмме показано движение вдоль начальной кривой спроса в сценарии А и сдвиг в случае сценария B:
Функция спроса и функция предложения могут быть использованы для решения задач рыночного равновесия и рыночной клиринговой цены.
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5